DHSWM：一种改进的WM多模式匹配算法

刘卫国，胡勇刚

(中南大学 信息科学与工程学院，湖南 长沙，410083)

摘要：针对WM算法的查找效率随着模式集规模的增大而降低的问题，提出一种改进算法。在预处理阶段，改变原有Hash表中的链表结构，采用双哈希法将模式串存放在Hash1表中指定的区间，Hash表中存放该存储区间的起始位置与区间长度；Prefix表用于判断模式集中是否存在与当前匹配窗口中文本前缀相同的模式；当Shift表中出现移动值为0时，根据后缀出现在模式串其他位置的信息计算匹配窗口可滑动的最大距离并存于Shift1表中。在查找阶段，采用双哈希法在Hash1表的某一区间中查找模式串，避免在大规模模式集情况下查找过长的模式链表，扩大匹配操作后匹配窗口滑动的距离，减少冗余的匹配操作，缩短查找时间。研究结果表明：在模式集规模较大时，改进后的算法显著地提高了匹配速度；当模式串数目超过5 000条时，改进算法的查找时间要比WM算法缩短40%~47%。

关键词：入侵检测；模式匹配；Wu-Manber算法；双哈希查找

中图分类号：TP393          文献标志码：A         文章编号：1672-7207(2011)12-3765-07

DHSWM: An improved multi-pattern matching algorithm based on WM algorithm

LIU Wei-guo, HU Yong-gang

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

Abstract: To resolve the problem that with the constant increase of the number of rules, the performance of Wu-Manber algorithm will become less efficient, an improved Wu-Manber algorithm named double Hash searching Wu-Manber algorithm (DHSWM) was proposed. In the pre-processing stage, the patterns were stored in specified intervals in Hash1 table by double Hash method while Hash table was used to store the parameters which indicate the start address of the interval and its length. Prefix table was used to determine whether the patterns in set and the text of current matching window had the same prefix. When the shifting distance was 0 in Shift table, Shift1 table was used to store the maximum sliding distance of matching window according to the suffixes appearing in other locations of pattern string. In the searching stage, double Hash method was used to look up patterns in the interval of Hash1 table to avoid searching for overlong linked list in the case of large scale pattern set. The sliding distance of matching window was enlarged after the matching procedure, so redundant matching operations was reduced and the search time was shortened. The results indicate that the algorithm can improve the speed of pattern matching when the scale of the pattern set is large. Compared with the WM algorithm, the DHSWM algorithm can reduce the search time by 40%-47% when the number of patterns is more than 5 000.

Key words: intrusion detection; pattern matching; Wu-Manber algorithm; double Hash searching

目前，大多数网络入侵检测系统(Network intrusion detection system，NIDS)的检测引擎采用的是模式匹配技术。测试结果表明，系统用于模式匹配的时间占到NIDS整个处理时间的30%，在网络流量密集情况下达80%^[1]。因此，通过改进模式匹配算法能有效地提高系统的检测速度。模式匹配算法包括单模式匹配算法和多模式匹配算法，常见的单模式匹配算法有Knuth-Morris-Patt(KMP)算法^[2]和Boyer-Moore (BM)算法^[3] 等。其中，BM算法应用较广泛, 其检测速度比KMP算法速度快3~5 倍，但在模式集规模较大时，BM算法的效率难以满足实际要求。多模式匹配算法包括Aho-Corasick(AC)算法^[4]和Wu-Manber (WM)算法^[5]等。AC算法是在KMP算法的基础上采用有限状态机原理构造模式树，在模式数目较多时能获得较高的查找效率，但通常构造模式树会占用大量的存储空间。WM算法主要基于字符跳跃思想和Hash散列技术，能大大提高匹配速度。近年来，很多研究者通过改进WM算法以获得更高的查找效率。Yang等^[6]结合QS算法思想^[7]提出了QWM算法，在查找阶段利用文本的前缀匹配信息判断是否进行匹配操作，并扩大窗口的最大滑动距离，改进后的算法比WM算法查找时间更少。Choi等^[8]通过增加最短模式串长度提出L⁺¹-MWM算法，可以得到更长的滑动距离；当最短模式串长度小于5时，该算法比WM算法平均查找时间减少38.87%。但改进后的算法在大规模模式集情况下，也像WM算法那样无法避免在哈希表中出现长度过长的模式链表，为此，研究者们通过减少在Hash表中的链表查找时间来提高匹配速度。吴冰等^[9]通过对特征串进行优化的方法，避免模式链表分支不平衡的问题，发现WM算法的查找效率能得到较大提高；Zhang等^[10]在查找时通过判断前缀链表中模式串地址是否在哈希表中链表地址范围来避免遍历哈希表中的链表，减少冗余的匹配操作，但需面临遍历前缀表中过长链表的问题。可见，如何在模式集规模不断增大的情况下保持WM算法的高效查找特性^[11-12]是一个必须解决的问题。本文作者采用双哈希查找来改进Wu-Manber算法(Double Hash searching Wu-Manber algorithm，DHSWM)，从而提高算法的查找效率。

1  WM算法分析

1.1  约定

定义1  字符集：由一定数目的字符构成的集合，记为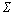，其字符个数记为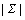。本文取∑为ASCII字符集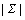，=128。

定义2  模式集：把用于匹配的字符串称为模式串，记为p，由多个模式串组成的集合叫模式集，记为P={p₁，p₂，…，p_i}。其中：；(j=1，2，…，l_i)。

定义3  滑动：在文本中发现与模式p_i完全匹配的字符串或者在匹配窗口中出现与模式中不同的字符时，将匹配窗口左移或右移，称为滑动。在滑动过程中跳跃的字符个数称为滑动距离。

定义4  模式匹配：给定字符集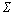，模式集为P，长度为n的文本串T=t₁t₂…t_n，t_i∈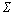(i=1，2，…，n)。若在T中能找到p_i，则匹配成功；若匹配失败，则将匹配窗口向左或向右滑动，继续匹配。在T中查找p_i的过程称为模式匹配。

1.2  WM算法描述

WM算法主要包含预处理和查找2个阶段。

1.2.1  预处理阶段

在预处理阶段，根据给定模式集P，确定匹配窗口长度m=min{length(p_i)}，并建立3个表：移动表(Shift表)、哈希表(Hash表)和前缀表(Prefix表)。移动表中存储的是在T中当前匹配窗口可滑动的距离。哈希表中存储的是具有相同后缀的模式链表的入口指针，前缀表中存储的是具有相同前缀的模式链表入口指针。

(1) Shift表的建立。在每次尝试匹配时，考虑一个长度为k的字符串，记为S。在Shift表中存储的是在匹配S时窗口可以滑动的距离，计算k个字符的一个整数匹配值作为Shift表的索引，假设S和Shift表中的第i个入口匹配，取所有模式串的前m个字符，存在2种情况：

① 若字符串S不在任何模式中出现，则可以安全地将匹配窗口向右滑动m-k+1个字符的距离，取Shift[i]=m-k+1。

② 若S在某些模式串中出现，则找出S在这些模式中出现的位置，取最右出现的位置。假设S在模式p_i的q处结束，且S在其他任何模式中并不结束于比q大的位置，取Shift[i]=m-q。

(2) Hash表的建立。取模式串的前m个字符，计算其k个字符后缀的哈希值，采用链表存储具有相同哈希值的模式串，哈希表中存储指向链表入口的指针。

(3) Prefix表的建立。Prefix表与Hash表类似，在建立时计算模式串k个字符前缀的哈希值，将具有相同前缀的模式串存储于同一链表中。

1.2.2  查找阶段

在查找阶段，计算当前匹配文本T的后k个字符的哈希值i，Hash表与Shift表采用相同的哈希值作为索引。当Shift[i]≠0时，将匹配窗口向右滑动Shift[i]个字符并继续扫描；当Shift[i]=0，则Hash[i]包含1个指针指向所有具有相同后缀的模式链表，遍历该链表，计算各个模式前k个字符的哈希值h和T中前k个字符的哈希值h’，若h≠h’，则可过滤掉后缀相同但前缀不同的模式串；若h=h’，则进行精确匹配，若成功则输出匹配结果，同时，将匹配窗口向右滑动1位；若匹配失败，则匹配窗口向右滑动1位，继续查找。

1.3  WM算法存在的主要问题

通过对WM算法的分析，可以发现以下问题：

(1) 在预处理阶段建立的3个表的功能有重叠，其中：Shift表用来判断是否进入精确匹配操作和记录滑动距离；Hash表存储后缀相同的模式串链表；Prefix表存储前缀相同的模式串链表。可以使用Shift表和Hash表来查找模式串，也可以使用Shift表和Prefix表来查找模式串，因此，Hash表和Prefix表在功能上可以相互替换。

(2) WM算法中使用Prefix表来过滤具有相同后缀但不同前缀的模式串，判断是否需要精确匹配。因此，Prefix表实际上是用来进行简单过滤操作，不需建立模式链表。

(3) 在Hash表中存储的指针指向具有相同后缀的模式链表，在进行精确匹配操作时需要遍历该链表。在实际应用的入侵检测系统中，模式集的规模通常很大^[13]，导致具有某些后缀的模式串链表长度较长，在查找时进入该链表会浪费大量查找时间。

(4) WM算法在匹配操作完成之后，不论匹配成功与否，匹配窗口的滑动距离均为1，不能跳过更多的字符，无法避免冗余的匹配操作，因此，滑动距离有扩大的可能。

这些问题使得实际应用中WM算法的查找效率降低，下面针对这些问题改进算法。

2  DHSWM算法

在DHSWM算法中，除了建立Shift表、Hash表和Prefix表3个基本表外，另外建立Shift 1表和   Hash 1表。Shift表存储当前匹配窗口可滑动的距离，当Shift表中移动值为0时，将查找模式串，Shift 1表用于存储进行匹配操作后匹配窗口可滑动的距离。在WM算法中，Hash表中采用链表结构存储模式串，DHSWM算法中不再维持原有的存储结构，Hash 1表存储模式集中的所有模式串，具有相同后缀的模式串采用双哈希法存储于表中的某一连续区间，在查找时只需访问表中的指定区间；Hash表中存储的参数表示该连续存储区间在Hash 1表中的起始位置与区间长度；当模式集给定时，模式头缀也就确定了。Prefix表用于判断模式集中是否存在与当前匹配窗口中文本前缀相同的模式。

2.1  算法描述

DHSWM算法与WM算法一样也包括预处理阶段和查找阶段。

2.1.1  预处理阶段

在预处理阶段，根据给定的模式集P，建立Shift表、Shift 1表、Hash表、Hash 1表以及Prefix表。

(1) Shift表和Shift 1表的建立。Shift表的建立与WM算法中相同，而Shift 1表在Shift表基础上建立。假设由k个字符组成的字符串S和Shift表中的第i个入口匹配，当Shift[i]=0即S出现在某些模式串的结尾时，找出S出现在模式串中除结尾外的其他位置，当S不出现在任何模式串中的其他位置时，取Shift1[i]为m-k+1；当S在某个模式串p_i中q’处结束，且S在其他任何模式中并不结束于比q’大的位置，取Shift1[i]=m-q’。

(2) Hash表和Hash1表的建立。当S出现在某些模式的结尾时，统计具有相同后缀S的模式个数，记为N，将这些同后缀的模式串采用双哈希法存储于Hash 1表中的连续区间内，令起始位置设为x，分配区间长度为y，则具有同后缀S的模式串存储于Hash1[x]至Hash 1[x+y-1]，Hash[i]存储(x，y)用于表示模式串在Hash1表中的位置。本文分配区间长度与相同后缀的模式串数目关联，y取最接近于2N的梅森素数^[14]，这样有3个好处：

① 快速得到素数。对于素数n=2，3，5，7，13，17等，则2ⁿ-1为梅森素数，本文只需取n=2，3，5，7即可满足要求。

② 当y取素数时，可以避免因y为二次函数返回值的倍数而导致使用二次函数存储或查找时进入死循环的问题。

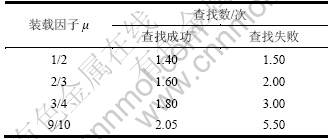
③ 使得装载因子约为1/2，有利于发挥双哈希法良好的查找性能。令μ为表中已用位置与表总长度的比值，称为装载因子。表1所示为不同装载因子时双哈希法查找成功和查找失败所预计的查找次数^[15]。

表1  双哈希法查找次数与装载因子关系表

Table 1  Relationship between searching times and load factors in double Hash searching

在存储和查找模式串时，均采用双哈希法对 Hash 1表进行操作。一次哈希函数返回字符串运算值与y求余的结果，二次哈希函数则返回1个小于y的非零整数值。例如，对模式p_i前m个字符p_i¹p_i²…p_i^m的一次哈希运算为：

(p_i¹*128^m-1+ p_i²*128^m-2+…+ p_i^m*128⁰)%y=

(…((p_i¹*128+ p_i²)*128+ p_i³)…+ p_i^m)%y=

 (…(((p_i¹*128+ p_i²)%y *128+ p_i³)%y*

128+ p_i⁴)…+ p_i^m)%y

二次哈希运算为：p_i¹%N+1。

(3) Prefix表的建立。Prefix表用于判断当前文本中的头缀是否在模式串的头缀中出现，存放的是布尔值。分别取每一个模式串前k个字符并计算其哈希值h，则Prefix[h]存放True，表示可以继续精确匹配过程，表中的其他位置存放False，表示直接将匹配窗口向前滑动。

2.1.2  查找阶段

在查找阶段，假设匹配窗口长度为m，每次匹配的字符串长度为k。查找步骤如下。

(1) 将匹配窗口与匹配文本T顶端对齐，T_p指向匹配窗口的结束位置，T_end指向文本结束位置。

(2) 当T_p＜T_end时，取当前匹配文本t₁t₂…t_m，计算文本的后k个字符t_m-k+1…t_m的哈希值h。

(3) 若Shift[h]>0，则窗口向右滑动Shift[h]个字符并返回步骤(2)；若Shift[h]=0，则转步骤(4)。

(4) 计算当前匹配文本前缀t₁…t_k的哈希值，检查Prefix表中的值，若为True，则转步骤(5)，若为False，则窗口向右滑动Shift1[h]个字符并转步骤(2)。

(5) 根据Hash表中给定的参数，采用双哈希法查找Hash 1表中对应的区间，并按文本与模式进行精确匹配，若匹配成功，则输出该模式并将匹配窗口向右滑动Shift1[h]个字符，然后转步骤(2)；若匹配不成功，则将匹配窗口向右滑动Shift1[h]个字符，然后转步  骤(2)。

2.2  算法应用范例

假设模式集P={still，trill，study，basic，stability}，文本T为“This chapter will introduce the basic concepts.”，则匹配窗口长度m=5，且令k=2。下面对WM算法和DHSWM算法的匹配过程进行对比分析。

预处理阶段WM算法和DHSWM算法建立的Shift表如表2所示。表中记录的值决定当前匹配窗口可滑动的距离，当Shift[i]=0时，进入精确匹配操作。DHSWM算法建立Shift1表如表3所示，表中记录完成匹配操作后匹配窗口可滑动的距离。WM算法中Prefix表存储具有相同头缀的模式链表，如图1所示，计算“st”的哈希值作为索引，Prefix[Hash(st)]存储的指针指向存放{stability，still，study}的链表入口。DHSWM算法改变Prefix表的结构，不再维持模式链表。表中除{st，tr，ba}对应的位置存放布尔值True外，其他均为False，表示只有当匹配文本的头缀出现在模式串的头缀时，才需进入精确匹配操作，如表4所示。

在Hash表的构建上，WM算法通过计算模式串中第m-1个和第m个字符的哈希值作为索引，将具有相同哈希值的模式串以链表存放，如图2(a)所示。Hash(ll)存储的指针指向存放{still，trill}的链表，当匹配窗口中文本的后缀为ll时，将遍历该链表；DHSWM算法中新建Hash 1表用于存储所有的模式串，Hash表中不再维持模式链表，如图2(b)所示。Hash(ll)中存储的是Hash1表中的起始位置和分配的连续区间的长度，其值分别为9和3，后缀为ll的模式串以双哈希法存放于Hash1[9]至Hash1[11]之间。

表2  Shift表

Table 2  Shift table

表3  Shift1表

Table 3  Shift1 table

图1  WM Prefix表结构图

Fig.1  Storage structure of WM Prefix table

图2  Hash表对比图

Fig.2  Comparison of Hash table

表4  DHSWM Prefix表

Table 4  DHSWM Prefix table

查找阶段如图3所示，其中：箭头指向当前匹配窗口的尾字符，右边数字为窗口滑动的距离。图3(a)所示为WM算法查找过程，整个过程经历13次匹配，其中出现2次移动值为0，第1次匹配不成功，无输出结果，将匹配窗口向右滑动1位；第2次匹配模式“basic”成功，将结果输出同时匹配窗口向右滑动1位。图3(b)所示为DHSWM算法查找过程，整个过程11次匹配，在出现移动值为0时，匹配操作完成后使用Shift 1表中的移动值，滑动距离增大至4。

图3  查找过程示意图

Fig.3  Searching process

3  实验与分析

测试数据：匹配文本取容量为6.82 MB的英文文档，模式串为在ASCII字符集内任意生成的字符串，最短模式串长度为5。模式集规模取10，50，100，200，500，1 000，5 000，10 000，20 000。编程环境为Windows XP和JDK1.5.0。

本文实验对比DHSWM算法与WM算法的查找时间，测试模式集规模为10~1 000时匹配成功的模式个数为5个，当模式集规模大于5 000时匹配成功的模式为50个。实验结果如表5所示，表中第1列为模式集中的模式数目，第2列和第3列分别为使用WM和DHSWM算法对文本匹配的查找时间。表中的查找时间取10次测试结果的平均值，第4列为DHSWM查找时间提高率。

表5  实验结果

Table 5  Result of experiment

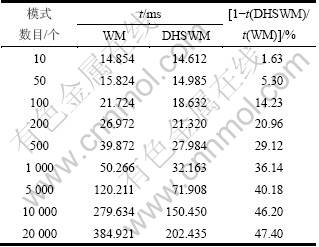
从表5可以看出：随着模式集规模的不断加大，DHSWM算法与WM算法相比查找效率越来越高。其原因主要如下。

(1) 增大了匹配窗口在匹配操作之后的滑动距离。在通常情况下，Shift表中的值大于0，匹配窗口可以通过滑动跳过大部分文本。当文本子串与模式串具有相同的后缀时，Shift表中就会出现值为0的情况，此时进入精确匹配操作；随着模式集规模的增大，Shift值为0的概率也随之增大。表6所示为模式串数目不同时，Shift表中移动值为0所占的比例。从表6可见：当模式串数目超过1 000条时，出现Shift[i]=0的概率超过30%，模式串数目为20 000条时达到57%，此时需频繁进入精确匹配操作，DHSWM算法在查找后采用Shift 1表中的移动值，这样比WM算法跳过更多的字符，从而减少了更多的冗余匹配操作。

(2) 避免了遍历模式链表。在WM算法中，Hash表以链表存储具有相同后缀的模式。表7所示为模式集规模不同时其对应Hash表中链表长度的分布情况。从表7可见：当模式集规模超过500时，开始出现长度较长(＞10)的链表；当模式集超过5 000时，出现长度超过50的链表，在查找过程中若进入此类链表中进行匹配操作，将耗费大量的查找时间。而DHSWM算法采用双哈希法进行查找，当装载因子为1/2时，查找的次数不超过2次，因此，使用双哈希法将缩短查找时间，从而提高查找效率。

表6  Shift表中移动值为0的比例

Table 6  Percentage of value 0 in Shift table

表7  WM Hash表中链表长度分布表

Table 7  Distribution of length of linked-list in WM Hash table              个

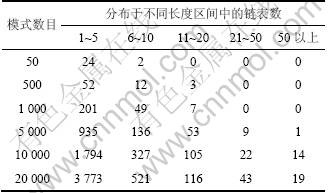
WM算法的查找时间与模式集规模线性正相关，本文使用双哈希法能有效地降低查找次数，使模式数目的增加对DHSWM算法中查找时间的影响远低于对WM算法中查找时间的影响。文献[6，8，10]中提出的改进算法均能有效地提高WM算法的查找效率，但其实验中模式数目均少于2 000条。本文将查找模式集规模扩大并有效地验证了模式集规模增加时，DHSWM算法更能有效地提高查找效率。

4  结论

(1) DHSWM算法中改变了Prefix表的存储结构，新增Shift 1表用于存放在匹配操作完成之后匹配窗口可滑动的距离，在查找模式串时通过过滤匹配文本的头缀，使用Prefix表判断是否进行精确匹配，减少了进入精确匹配操作的次数。在完成匹配操作后，匹配窗口采用Shift 1表中的滑动距离，可以跳过更多的文本字符，避免了更多的冗余匹配操作，缩短了查找   时间。

(2) DHSWM算法改变了Hash表的存储结构，新增Hash 1表用于存放所有模式串，在查找模式串时不再采用WM算法中遍历模式链表的匹配操作，使用双哈希法对Hash 1表进行查找匹配模式串。在模式数目较多的情况下，避免了遍历长度较长的模式链表，减少了匹配次数，从而有效地提高了查找效率。

(3) 当模式集规模较大时，DHSWM算法的查找性能更优。目前，网络数据流量日益增大，入侵规则模式集的规模不断增加，高效的检测引擎有利于实现高速网络数据流的实时入侵检测。

参考文献：

[1] Fisk M, Varghese G. An analysis of fast string matching applied to content-based forwarding and intrusion detection[R]. San Diego: University of California, 2002: 1-9.

[2] Knuth D E, Morris H, Pratt V R．Fast pattern matching in strings[J]. SIAM Journal on Computing, 1977, 6(2): 323-350.

[3] Boyer R S, Moore J S. A fast string searching algorithm[J]. Communications of the ACM, 1977, 20(10): 762-772.

[4] Aho A V, Corasick M J. Efficient string matching: An aid to bibliographic search[J]. Communications of the ACM, 1975, 18(6): 333-340.

[5] Wu S, Manber U. A fast algorithm for multi-pattern searching[R]. Tuscon: University of Arizona, 1994: 1-11.

[6] YANG Dong-hong, XU Ke. An improved Wu-Manber multiple patterns matching algorithm[C]//The 25th IEEE International Performance, Computing, and Communications Conference. Phoenix, USA, 2006: 675-680.

[7] Sunday D M. A very fast substring search algorithm[J]. Communications of the ACM, 1990, 33(8): 132-142.

[8] Choi Y H, Jung M Y, Seo S W. L⁺¹-MWM: A fast pattern matching algorithm for high-speed packet filtering[C]//2008 Proceedings IEEE INFOCOM. Phoenix, USA, 2008: 261-265.

[9] 吴冰, 云晓春. 基于网络的恶意代码检测技术[J]. 通信学报, 2007, 28(11): 87-91.
WU Bing, YUN Xiao-chun. Network-based malcode detection technology[J]. Journal on Communications, 2007, 28(11): 87-91.

[10] ZHANG Bao-jun, CHEN Xiao-ping, PING Ling-di. Address filtering based Wu-Manber multiple patterns matching algorithm[C]//Proceedings of the 2009 Second International Workshop on Computer Science and Engineering (WCSE 2009). Qingdao, China, 2009: 408-412.

[11] CAO Bin, LAN Hua, SHEN Xuan-jing. Application of set-based multi-pattern matching algorithm for intrusion detection system[C]//2008 Second International Symposium on Intelligent Information Technology Application. Piscataway, USA, 2008: 706-710.

[12] 李雪, 薛一波. 一种适用于大规模特征集的快速匹配算法[J]. 计算机工程与应用, 2007, 43(34): 168-170.
LI Xue, XUE Yi-bo. High-performance string matching algorithm for large scale string set[J]. Computer Engineering and Applications, 2007, 43(34): 168-170.

[13] Wang J S, Kwak H K, Jung Y J. A fast and scalable string matching algorithm using contents correction signature hashing for network IDS[J]. IEICE Electronics Express, 2008, 5(22): 949-953.

[14] 李伟勋. Mersenne数M_p都是孤立数[J]. 数学研究与评论, 2007, 27(4): 693-696.
LI Wei-xun. All Mersenne numbers are anti-sociable numbers[J]. Journal of Mathematical Research and Exposition, 2007, 27(4): 693-696.

[15] 塞奇威克. Java 算法[M]. 赵文进, 译. 北京: 清华大学出版社, 2004: 474-478.
Sedgewick R. Algorithm in Java[M]. ZHAO Wen-jin, trans. Beijing: Tsinghua University Press, 2004: 474-478.

(编辑 陈灿华)

收稿日期：2010-12-06；修回日期：2011-03-10

基金项目：国家自然科学基金资助项目(61073187)

通信作者：刘卫国(1963-)，男，湖南祁阳人，博士，教授，从事网络与信息安全、智能信息处理研究；电话：0731-88830062；E-mail：liuwg@csu.edu.cn