一种亚弹黏塑性晶体塑性模型的显示积分算法
来源期刊:中国有色金属学报(英文版)2014年第7期
论文作者:K. ZHANG B. HOLMEDAL S. DUMOULIN O. S. HOPPERSTAD
文章页码:2401 - 2407
关键词:晶体塑性;亚弹性;超弹性;向前欧拉积分法
Key words:crystal plasticity; hypo-elasticity; hyper-elasticity; forward Euler integration
摘 要:建立了一种速率相关的晶体塑性模型的显示积分算法。该晶体塑性模型将速度梯度张量分解为晶格和塑性部分来描述运动学,并利用亚弹性方程和Jaumann应力率计算柯西应力。该晶体塑性模型及新提出的显示积分算法已被用于一种商业有限元程序,并模拟了多晶的单轴压缩和轧制实验过程。实验结果表明,该晶体塑性模型的显示积分算法具有很高的精确性和可靠性。相对利用乘法分解变形梯度张量方法建立的超弹黏塑性模型及其对应的显示积分算法,该亚弹性模型的显示积分算法除了速度稍快外,其精确性与超弹性模型是一样的。
Abstract: An explicit integration scheme for rate-dependent crystal plasticity (CP) was developed. Additive decomposition of the velocity gradient tensor into lattice and plastic parts is adopted for describing the kinematics; the Cauchy stress is calculated by using a hypo-elastic formulation, applying the Jaumann stress rate. This CP scheme has been implemented into a commercial finite element code (CPFEM). Uniaxial compression and rolling processes were simulated. The results show good accuracy and reliability of the integration scheme. The results were compared with simulations using one hyper-elastic CPFEM implementation which involves multiplicative decomposition of the deformation gradient tensor. It is found that the hypo-elastic implementation is only slightly faster and has a similar accuracy as the hyper-elastic formulation.
Trans. Nonferrous Met. Soc. China 24(2014) 2401-2407
K. ZHANG1, B. HOLMEDAL1, S. DUMOULIN2, O. S. HOPPERSTAD3,4
1. Department of Materials Science and Engineering, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway;
2. SINTEF Materials and Chemistry, NO-7465 Trondheim, Norway;
3. Department of Structural Engineering, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway;
4. Structural Impact Laboratory (SIMLab), Center for Research-based Innovation, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
Received 17 October 2013; accepted 11 April 2014
Abstract: An explicit integration scheme for rate-dependent crystal plasticity (CP) was developed. Additive decomposition of the velocity gradient tensor into lattice and plastic parts is adopted for describing the kinematics; the Cauchy stress is calculated by using a hypo-elastic formulation, applying the Jaumann stress rate. This CP scheme has been implemented into a commercial finite element code (CPFEM). Uniaxial compression and rolling processes were simulated. The results show good accuracy and reliability of the integration scheme. The results were compared with simulations using one hyper-elastic CPFEM implementation which involves multiplicative decomposition of the deformation gradient tensor. It is found that the hypo-elastic implementation is only slightly faster and has a similar accuracy as the hyper-elastic formulation.
Key words: crystal plasticity; hypo-elasticity; hyper-elasticity; forward Euler integration
1 Introduction
Crystal plasticity (CP) models originate from the physical aspect of plastic deformation, i.e. slip dominated plastic deformation [1]. Constitutive laws of single crystals together with homogenization methods across polycrystalline aggregates define the polycrystal plasticity model [2,3]. Mechanical properties, texture evolution and other material phenomena can be simulated using CP models [2-5]. The main inputs into CP models are initial texture and material parameters.
One key component of a crystal plasticity model at single-grain level is the determination of shear strains or shear strain rates on slip systems, which can generally be solved using two different approaches, either rate- independent or rate-dependent. For the rate-independent method, the shear strain is determined to accommodate the prescribed plastic deformation using a minimum dissipation energy assumption [1]. Only the slip systems for which the resolved shear stress equals the critical resolved shear stress are considered to be active. It can be implemented numerically by solving linear equations or using the simplex method with high computational efficiency [6]. However, due to the Taylor ambiguity, an additional criterion is needed [7]. The rate-dependent crystal plasticity (RDCP) model assumes that all slip systems are active and uses a viscoplastic flow rule. Without Taylor ambiguity, RDCP could lead to numerical instabilities of integration because most metals exhibit a weak rate dependence at room temperature [8]. Since first introduced by PEIRCE et al [9], the crystal plasticity theory implemented in the finite element method (CPFEM) has matured into a whole family of constitutive and numerical formulations that have been applied to a broad variety of crystal mechanical problems [3]. CPFEM has both theoretical and practical advantages. First, grains are represented by single or multiple elements while both stress equilibrium and strain compatibility can be fulfilled at boundaries. Second, complex boundary conditions are easily specified in the FEM code. Hence, CPFEM is applicable to simulations of engineering processes. The main drawback of CPFEM is the huge computational cost and the numerical instabilities [2]. Thus, robust and efficient integration schemes are required to reduce computational cost and improve the stability [2,8,10-14].
DUMOULIN et al [2] implemented and evaluated three different integration schemes for RDCP, including two forward Euler methods and one implicit integration method. Multiplicative decomposition of the deformation gradient tensor F was used to describe the kinematics and a hyper-elastic formulation was used for the calculation of the Cauchy stress. Rotation of the crystal lattice was obtained by polar decomposition of the elastic deformation gradient tensor Fe. Among these three integration methods, the forward Euler integration scheme proposed by GRUJICIC and BATCHU (GB) [14] was proved to be stable, accurate and the fastest. The RDCP model together with the GB forward Euler integration scheme has also been implemented into a commercial finite element code, LS-DYNA via a user defined subroutine UMAT [15]. This model implementation is referred to as hyper-CPFEM in the following since hyper-elasticity is assumed.
In the current work, a new explicit integration scheme for rate-dependent viscoplastic crystal plasticity has been developed. Different from the constitutive models employed by DUMOULIN et al [2], additive decomposition of the velocity gradient tensor L is employed for the kinematics; hypo-elasticity is assumed for the material and Jaumann stress rate is applied. In the crystal plasticity theory, the hyper- and hypo-elastic formulations should give the same results in terms of the plastic deformation. There is small difference in the elastic part while details about the hypo-elastic and hyper-elastic theories can be found in Ref. [16]. The hypo-elastic theory is commonly applied in the continuum plasticity for metals and alloys due to their small elastic strains. Compared with the hyper-elastic crystal plastic framework, the hypo-elastic counterpart has a simpler mathematical formulation and is easier to implement. Hence, the hypo-elastic crystal plasticity model has a potential to speed up the calculations. However, the accuracy and reliability of stress calculation and texture prediction should be evaluated due to the different formulations employed.
The kinematics, kinetics and crystal plasticity models are described in section 2. A new explicit integration scheme is proposed in section 3. The RDCP model has been implemented into LS-DYNA and is termed hypo-CPFEM in the following. The accuracy and efficiency of this new integration scheme are evaluated through numerical simulations and a comparison with the hyper-CPFEM which are shown in section 4, while general conclusions are made in section 5.
2 Kinematics and crystal plasticity models
The model employed in this work is briefly given here while more details can be found in Refs. [17,18]. It includes anisotropic elastic deformation and assumes that all plastic deformation occurs via dislocation slip on
2.1 Kinematics
All the equations described in the following are formulated in the initial crystal frame unless specified otherwise. The imposed velocity gradient L can be additively decomposed into symmetric and skew- symmetric parts:
L=D+W (1)
where D is the symmetric deformation rate tensor and W is the skew-symmetric spin tensor. Deformation of single crystals has been attributed to a combination of plastic flow due to crystallographic slips and lattice distortion. Lattice distortion includes elastic distortion and rigid body rotation of the crystal lattice. Thus, for single crystals, the deformation rate D and spin W can be further decomposed into lattice and plastic parts as follows:
D=De+Dp (2)
W=W*+Wp (3)
where De represents the elastic deformation rate of the lattice, while Dp is the plastic deformation rate caused by crystallographic slip; W* represents the lattice rigid spin, while Wp is the spin due to slip activities. Dp and Wp can be expressed by the shear rates 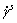 on all slip systems:
on all slip systems:
 (4)
(4)
 (5)
(5)
with
 (6)
(6)
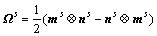 (7)
(7)
where ms is the unit vector defining slip direction, while ns is the unit slip plane normal vector, for the slip system s (where s=1-12 for FCC metals); ms and ns are not affected by crystallographic slip but will be rotated by the lattice spin W* as
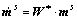 (8)
(8)
 (9)
(9)
2.2 Kinetics
The resolved shear stress τs on the slip system s can be expressed as
τs =σ: Ps (10)
where σ is the Cauchy stress tensor. For rate-dependent crystal plasticity, the shear rate on slip systems is often calculated using a power-law type equation:
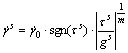 (11)
(11)
where 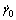 is a reference shearing rate, m is the instantaneous strain rate sensitivity and gs represents the slip resistance which evolves during the plastic deformation of single grains. The evolution laws of gs or hardening models will be discussed in section 2.3.
is a reference shearing rate, m is the instantaneous strain rate sensitivity and gs represents the slip resistance which evolves during the plastic deformation of single grains. The evolution laws of gs or hardening models will be discussed in section 2.3.
During distortion of single crystals, a coordinate system attached to the lattice will co-rotate with the lattice. The co-rotational lattice frame is related to the fixed lattice frame by a rotation tensor R which is orthogonal and updated by the lattice spin tensor W*:
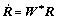 (12)
(12)
In the co-rotational frame, Hooke’s law can be expressed in the rate form as
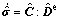 (13)
(13)
where 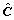 is a fourth-order elastic modulus tensor and
is a fourth-order elastic modulus tensor and 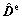 is the elastic deformation rate tensor, both in the co-rotational frame. The fourth-order tensor
is the elastic deformation rate tensor, both in the co-rotational frame. The fourth-order tensor 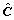 accounts for the elastic anisotropy of the cubic lattice. It is assumed to be invariant to plastic deformation and is kept constant in the co-rational lattice frame. Expressed in the orthonormal basis associated with the crystal lattice, it reads (in Voigt notation):
accounts for the elastic anisotropy of the cubic lattice. It is assumed to be invariant to plastic deformation and is kept constant in the co-rational lattice frame. Expressed in the orthonormal basis associated with the crystal lattice, it reads (in Voigt notation):
 (14)
(14)
where c11, c12 and c44 are three independent elastic constants. 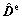 can be computed by transforming De from the fixed lattice frame to the co-rotational frame as
can be computed by transforming De from the fixed lattice frame to the co-rotational frame as
 (15)
(15)
where the upper script T means transpose of a tensor or matrix. Then Jaumann stress rate, 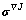 , is now defined by transforming
, is now defined by transforming 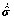 into the fixed coordinate system:
into the fixed coordinate system:
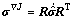 (16)
(16)
Finally, the material time derivative of the stress tensor is obtained:
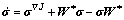 (17)
(17)
2.3 Hardening model
Material hardening is captured at slip system level through gs in Eq.(11) . The hardening law used in this work assumes that the critical resolved shear stress, gs, initially equal to g0, evolves through
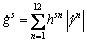 (18)
(18)
where hsn is the instantaneous strain hardening matrix; s and n are indices referring to slip systems. In this work, hsn is described phenomenologically by a saturation-type law [8,19]:
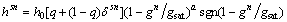 (19)
(19)
where δsn=1 for s=n and otherwise zero; h0, gsat and a are material parameters, representing the reference self-hardening coefficient, the saturation values of slip resistance and the hardening exponent, respectively. The parameter q represents latent hardening.
2.4 Update of grain orientations and texture
If the velocity gradient L′ is prescribed in the sample frame, L in the initial lattice frame is obtained by the transformation
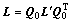 (20)
(20)
where the transformation matrix Q0 depends on the Euler angles (φ1, Φ, φ2). The transformation matrix Q from the global frame to the current co-rotational lattice frame is updated by
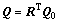 (21)
(21)
Euler angles of single grains during deformation can be calculated from Q and are used to represent the texture.
3 Integration algorithm
The crystal plasticity model described above has been implemented into LS-DYNA through a user defined material subroutine. The key input includes material parameters and initial grain orientations. Mechanical response and deformation texture can then be predicted.
For the time integration, a fully explicit scheme based on the forward Euler method is adopted. This method is simple, robust but only conditionally stable and requires small time steps. The main steps of the explicit scheme are summarized below, where all variables at time tn are known and the variables at tn+1=tn+Δt are to be determined.
1) Compute the resolved shear stress 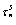 on each slip system using Eq. (10);
on each slip system using Eq. (10);
2) Compute the slip rate 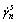 using Eq.(11) ;
using Eq.(11) ;
3) Compute  and
and 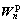 using Eq.(4) and Eq.(5) ;
using Eq.(4) and Eq.(5) ;
4) Compute 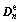 and
and 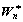 using Eq.(2) and Eq.(3) , where D and W are constant during the current time step;
using Eq.(2) and Eq.(3) , where D and W are constant during the current time step;
5) Compute the Jaumann stress rate 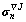 using Eq.(13) , Eq.(15) and Eq.(16) ;
using Eq.(13) , Eq.(15) and Eq.(16) ;
6) Compute  using Eq.(17) and update σn+1:
using Eq.(17) and update σn+1:
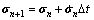 (22)
(22)
7) Update 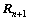 using a second-order scheme [20] as
using a second-order scheme [20] as
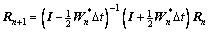 (23)
(23)
8) Update internal variables and update the critical resolved stress 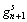 using equations described in section 2.3;
using equations described in section 2.3;
9) Update slip direction vectors, 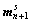 , and slip plane normal vectors,
, and slip plane normal vectors, 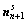 , using the second-order method:
, using the second-order method:
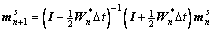 (24)
(24)
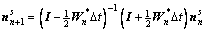 (25)
(25)
10) Compute  and
and 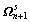 from
from 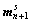 and
and 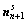 using Eq.(6) and Eq.(7) ;
using Eq.(6) and Eq.(7) ;
11) Update the grain orientation matrix  using Eq.(21) .
using Eq.(21) .
4 Numerical study and discussion
To evaluate the hypo-elastic formulation used here and the integration algorithm proposed in this work, two numerical studies have been conducted. The first one is the simulation of uniaxial compression of OFHC copper with initially random texture while the second one is the texture prediction after rolling of the same material. The hyper-CPFEM model implemented by DUMOULIN et al [2] with the GB integration scheme has also been used for the above simulation cases. Predicted results from the two CPFEM formulations will be compared in order to evaluate their performance in terms of accuracy and efficiency.
The material parameters are given similar values as reported in the work of KALIDINDI et al [19], as shown in Table 1. 1000 random orientations are used to represent the initial texture of the material and the {111} pole figure is shown in Fig. 1. The representative volume (RVE) has dimensions of 2 mm × 2 mm × 2 mm. The RVE is meshed with 1000 equal-sized 8-integration point solid elements and each element is assigned one orientation and hence represents one grain, as shown in Fig. 2. Mass scaling is used to speed up the simulations with a scaling factor of 108. All simulations were performed on a work-station with Intel Xeon E5620 CPU (2.4 GHz) and 12G memory, and 8 threads were used simultaneously for each simulation.
Table 1 Model parameters used in simulations

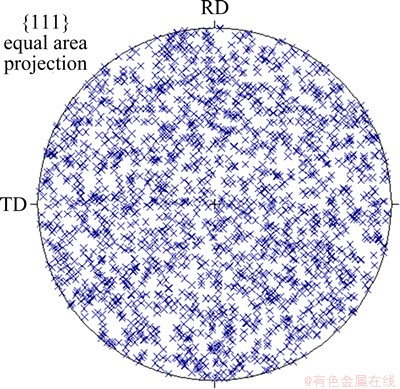
Fig. 1 Initial {111} equal area pole figure of 1000 orientations

Fig. 2 RVE with 1000 grains
4.1 Uniaxial compression
The RVE is compressed along the x-direction with a speed of 0.01 mm/s to 70% thickness reduction, namely, the deformation time is 140 s. The surfaces along y- and z- direction are free to move.
The stress-strain curves from simulations using the hypo-CPFEM and the hyper-CPFEM respectively are shown in Fig. 3, where the experimental data from Ref. [19] are also shown. It can be seen that the hypo-CPFEM and the hyper-CPFEM give the same stress versus strain response. The agreement between the predicted curves and the experimental ones is reasonable. The CPU time is shown in Table 2. Both CPFEM models have similar time efficiency, but the hypo-CPFEM is slightly faster.
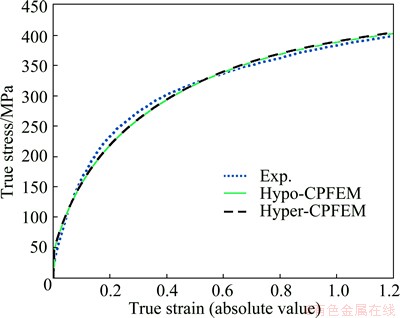
Fig. 3 Stress-strain curves from CPFEM simulations and experiment
Table 2 CPU time for simulations using two CPFEM models

The good agreement between the predictions by the two CPFEM models validates accuracy and reliability of the crystal plasticity formulations as well as the integration method used for the hypo-CPFEM. Moreover, the fact that the hypo-CPFEM and the hyper-CPFEM give identical stress predictions illustrates that both hypo-elasticity and hyper-elasticity are valid assumptions for crystal plasticity models of metals.
4.2 Rolling texture prediction
For the rolling simulation, periodic boundary conditions were applied on all faces of the RVE. The RVE was compressed along the z-axis with a speed of 0.02 mm/s to a thickness reduction of 70%. It was allowed to move along the x-axis freely while the deformation along the y-direction was constrained. The Euler angles after deformation at all integration points were output into files, and the orientation distribution function (ODF) was computed using the series expansion method with lmax=22 and Ψ0=7.5°.
Figure 4 shows the ODFs predicted by both hypo-CPFEM and hyper-CPFEM after rolling to 70% thickness reduction, while the corresponding CPU time is shown in Table 3. The ODF shows a typical rolling texture of FCC metals made of Brass, Goss, S, and copper texture components [18], which qualitatively validates the correctness of the texture updating algorithms employed. Furthermore, the ODFs from the two simulations show excellent agreement with each other. It is reminded that the texture is updated by the tensor Re which is obtained from the polar decomposition of the elastic deformation gradient tensor in the hyper-CPFEM. However, R which is updated using W* is employed for updating the texture in the hypo-CPFEM. The excellent agreement between the texture predictions demonstrates that both texture updating methods are equally accurate. Similar to the uniaxial compression case, the hypo-CPFEM is slightly faster (~10%) than the hyper-CPFEM, as shown in Table 3.
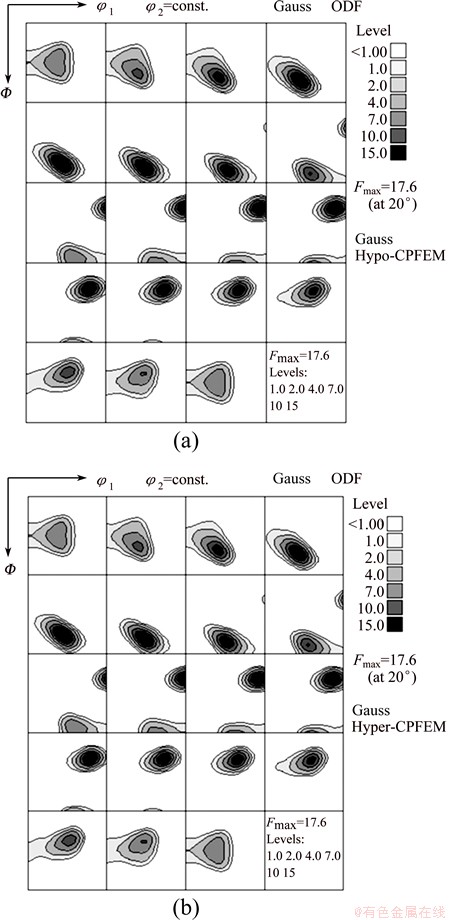
Fig. 4 Orientation distribution function (ODF) after 70% thickness reduction in rolling predicted by hypo-CPFEM (a) and hyper-CPFEM (b)
Table 3 CPU time for rolling using two CPFEM models

5 Conclusions
1) A new forward Euler integration scheme is proposed for rate-dependent crystal plasticity, which employs the additive decomposition of the velocity gradient and uses a hypo-elasticity formulation for the stress calculation. The RDCP model with the new integration scheme has been implemented into the commercial finite element code LS-DYNA.
2) This implementation is validated by comparison with a hyper-elastic formulation through two numerical tests. It is shown that the hypo-CPFEM is accurate for stress predictions, and the numerical algorithm for updating texture is validated by comparison with hyper-CPFEM predictions.
3) Comparison of predictions by the hypo-CPFEM and by the hyper-CPFEM shows that the two models have equal accuracy when predicting stress and texture while the hypo-CPFEM is slightly more efficient.
4) Finally, the current forward Euler integration method, and thereby the hypo-CPFEM, can be further improved without loss of accuracy, through sub-stepping; this is part of an on-going work.
References
[1] TAYLOR G I. Plastic strain in metals [J]. Journal of Institute of Metals, 1938, 62: 307-324.
[2] DUMOULIN S, HOPPERSTAD O S, BERSTAD T. Investigation of integration algorithms for rate-dependent crystal plasticity using explicit finite element codes [J]. Computational Materials Science, 2009, 46(4): 785-799.
[3] ROTERS F, EISENLOHR P, HANTCHERLI L, TJAHJANTO D D, BIELER T R, RAABE D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications [J]. Acta Materialia, 2010, 58(4): 1152-1211.
[4] CHENG Li-dong, WANG Zhen-long. Scale effect mechanism on micro rod upsetting deformation analyzed by crystal plasticity model [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(10): 2444-2450.
[5] LI Sai-yi. Application of crystal plasticity modeling in equal channel angular extrusion [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 170-179.
[6] van HOUTTE P. A comprehensive mathematical formulation of an extended Taylor–Bishop–Hill model featuring relaxed constraints, the Renouard–Wintenberger theory and a strain rate sensitivity model [J]. Textures and Microstructures, 1989, 8-9: 313-350.
[7] DELANNAY L, KALIDINDI S R, van HOUTTE P. Quantitative prediction of textures in aluminium cold rolled to moderate strains [J]. Materials Science and Engineering A, 2002, 336(1-2): 233-244.
[8] ZHANG H, DONG X, WANG Q, ZENG Z. An effective semi-implicit integration scheme for rate dependent crystal plasticity using explicit finite element codes [J]. Computational Materials Science, 2012, 54: 208-218.
[9] PEIRCE D, ASARO R J, NEEDLEMAN A. An analysis of nonuniform and localized deformation in ductile single crystals [J]. Acta Metallurgica, 1982, 30(6): 1087-1119.
[10] LING X, HORSTEMEYER M F, POTIRNICHE G P. On the numerical implementation of 3d rate-dependent single crystal plasticity formulations [J]. International Journal for Numerical Methods in Engineering, 2005, 63(4): 548-568.
[11] KUCHNICKI S N,  A M, RADOVITZKY R A. Efficient and robust constitutive integrators for single-crystal plasticity modeling [J]. International Journal of Plasticity, 2006, 22(10): 1988-2011.
A M, RADOVITZKY R A. Efficient and robust constitutive integrators for single-crystal plasticity modeling [J]. International Journal of Plasticity, 2006, 22(10): 1988-2011.
[12] LI H W, YANG H, SUN Z C. A robust integration algorithm for implementing rate dependent crystal plasticity into explicit finite element method [J]. International Journal of Plasticity, 2008, 24(2): 267-288.
[13] KUCHNICKI S N, RADOVITZKY R A,  A M. An explicit formulation for multiscale modeling of bcc metals [J]. International Journal of Plasticity, 2008, 24(12): 2173-2191.
A M. An explicit formulation for multiscale modeling of bcc metals [J]. International Journal of Plasticity, 2008, 24(12): 2173-2191.
[14] GRUJICIC M, BATCHU S. Crystal plasticity analysis of earing in deep-drawn OFHC copper cups [J]. Journal of Materials Science, 2002, 37(4): 753-764.
[15] HALLQUIST J O. LS-DYNA keyword user’s manual version 971 [M].California: Livermore Software Technology Corporation, 2007.
[16] BELYTSCHKO T, LIU W K, MORAN B. Nonlinear finite elements for continua and structures [M]. New York: John Wiley, 2000.
[17] BUCHHEIT T E, WELLMAN G W, BATTAILE C C. Investigating the limits of polycrystal plasticity modeling [J]. International Journal of Plasticity, 2005, 21(2): 221-249.
[18] KOCKS U F,  C N, WENK H R.Texture and anisotropy: Preferred orientations in polycrystals and their effect on materials properties [M].Cambridge: Cambridge University Press, 2000.
C N, WENK H R.Texture and anisotropy: Preferred orientations in polycrystals and their effect on materials properties [M].Cambridge: Cambridge University Press, 2000.
[19] KALIDINDI S R, BRONKHORST C A, ANAND L. Crystallographic texture evolution in bulk deformation processing of fcc metals [J]. Journal of the Mechanics and Physics of Solids, 1992, 40(3): 537-569.
[20] HUGHES T Jr, WINGET J. Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis [J]. International Journal for Numerical Methods in Engineering, 1980, 15(12): 1862-1867.
K. ZHANG1, B. HOLMEDAL1, S. DUMOULIN2, O. S. HOPPERSTAD3,4
1. Department of Materials Science and Engineering, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway;
2. SINTEF Materials and Chemistry, NO-7465 Trondheim, Norway;
3. Department of Structural Engineering, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway;
4. Structural Impact Laboratory (SIMLab), Center for Research-based Innovation, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
摘 要:建立了一种速率相关的晶体塑性模型的显示积分算法。该晶体塑性模型将速度梯度张量分解为晶格和塑性部分来描述运动学,并利用亚弹性方程和Jaumann应力率计算柯西应力。该晶体塑性模型及新提出的显示积分算法已被用于一种商业有限元程序,并模拟了多晶的单轴压缩和轧制实验过程。实验结果表明,该晶体塑性模型的显示积分算法具有很高的精确性和可靠性。相对利用乘法分解变形梯度张量方法建立的超弹黏塑性模型及其对应的显示积分算法,该亚弹性模型的显示积分算法除了速度稍快外,其精确性与超弹性模型是一样的。
关键词:晶体塑性;亚弹性;超弹性;向前欧拉积分法
(Edited by Hua YANG)
Corresponding author: K. ZHANG, Tel: +47-73594004; E-mail: kai.zhang@ntnu.no
DOI: 10.1016/S1003-6326(14)63363-X

