用Hartley变换实现连续动力学系统参数模型直接辨识

贺尚红，陈慧勇，杨　甫

(长沙理工大学 汽车与机械工程学院，湖南 长沙，410076)

摘要：针对大多数物理系统是由一组微分方程表示的连续时间系统，难以获得信号的各阶微分，连续动力学系统参数模型无法直接辨识的问题，借助Hartley正、逆变换及其微分性质，在频域对信号去噪，获得信号及其微分的估计值，建立参数模型直接估计的最小二乘算法。通过数字仿真分别辨识一个二阶系统和四阶系统，研究频率指数M和时间T与辨识精度的关系，给出辨识时参数选择的基本原则。此外，运用此方法对某冷轧机液压自动厚控系统参数模型进行辨识，结果表明：该方法对噪声具有较强的抑制能力，是一种简单实用的辨识方法。

关键词：系统辨识；Hartley变换；线性连续系统

中图分类号：TH3         文献标识码：A         文章编号：1672-7207(2007)01--

Direct identification of the parameter model of continuous dynamic

system using Hartley transformation

HE Shang-hong, CHEN Hui-yong, YANG Fu

(School of Automobile and Mechanical Engineering, Changsha University of Science and Technology, Changsha 410076, China)

Abstract: Based on most of the real dynamic systems are continuous in time and can be represented by a set of differential equations, it is difficult to acquire the differentials of input and output signal, the parameter model of continuous time system cannot be identified directly, according to Hartley transformation, inverse transformation and its differential property, the noise was filtered in frequency domain, and the estimators of differential signal were obtained. So, the least-squares algorithm for direct identification of parameter model was formulated. Two models with second order and fourth order were estimated, and the relationship between the frequency index M and the accuracy of identification was investigated, and some tips about design of parameter of Hartley transformation were outlined. Finally, the parameter model of a hydraulic automatic gage control system (HAGC) of cold rolling mill was identified. The result indicates that the method can be used to suppress noise effectively, and it is a simple and practical method.

Key words: system identification; Hartley transformation; continuous-time system

实际物理系统通常是由一组(偏)微分方程及若干约束关系组成的连续时间系统。虽然连续传递函数模型可通过辨识系统的离散模型间接得到，但这种间接方法有时存在原理和数字计算上的缺陷，会改变系统的稳定性^[1]。连续模型参数直接辨识最大的困难在于不能直接测量含噪声的输入、输出信号的各阶微分，而对微分的近似处理会加剧噪声的影响^[2]。通常对信号施加一个动态线性算子以获取等价辨识模型^[1-2]。多重积分法将系统微分方程转化成等价的积分方程，但会产生积分初值问题^[3]。调制函数法对系统初始条件和终端条件没有限制，信号的微分被调制函数的微分所代替，避免了对信号的微分处理^[4]。HE Shang-hong等^[5-7]对该类辨识进行了研究，并应用于大型工业系统动态数学模型辨识。该类方法关键的问题是调制函数的合理设计，计算工作量较大。Hartley变换是R.V.Hartley提出的一种傅里叶变换的等效形式，具有与傅里叶变换类似的特性^[8-10]：在此，本文作者利用Hartley变换相关性质建立连续动力学系统参数模型辨识的直接方法，通过数字仿真和工业试验验证该方法的有效性。

1　Hartley变换

Hartley变换的核函数cas ωt=cos ωt+sin ωt是傅里叶变换核函数exp(j ωt)=cos ωt +jsin ωt的实部与虚部之和。对于连续信号f(t)，若下面的积分存在，则其Hartley变换定义为^[8]：

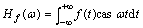。        (1)

其中：cas ωt=cos ωt+sin ωt，其相应的反变换为：

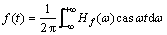。       (2)

从变换H_f(ω)可以看出，Hartley变换与傅里叶变换非常相似，二者之间存在紧密的关系。但是，必须指出的是，Hartley变换虽然是实值变换，但它也是一种一一对应的变换，不会导致信号任何频率信息的丢失^[11]。Hartley变换具有如下性质。

a. 尺度变换性质。当K≠0时，有：

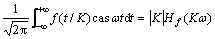。    (3)

b. 微分性质。设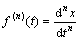，则f⁽ⁿ⁾(t)的连续Hartley变换为：

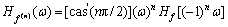。  (4)

性质b.对连续模型辨识非常重要。利用这一性质可得到信号各阶微分的Hartley谱，逆变换后获取信号的各阶微分。

在实际计算过程中，常采用离散Hartley变换。

设f(n)(n=0，1，…，N-1)为一实值序列，它的离散Hartley变换定义为：

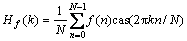。     (5)

其中：k=0，1，…，N-1。式(5)的反变换为：

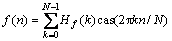。       (6)

然而，直接运用Hartley离散变换通常并不能获得连续变换的很好近似，这里采用复化辛浦生求积公式进行Hartley变换：

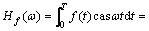
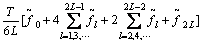。   (7)

式中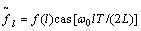：；ω₀=2π/T；2L+1为采

样数据序列长度；T为信号持续时间。

2　参数模型直接辨识原理

对于单输入单输出线性连续动力学系统，其微分方程模型可以表示为：

要辨识式(8)，关键是要获得u^(j)(t)和y⁽ⁱ⁾(t)，而直接对信号进行近似处理会产生噪声放大问题。为有效解决这个问题，利用Hartley变换及其微分的性质获得输入输出信号u(t)和y(t)及其各阶微分的Hartley谱

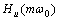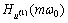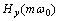，，…，，，，…，。其中：ω₀=2π/T，m=0，

±1，±2，…，±M，是Hartley谱的频率指数。然后，

采用Hartley反变换获得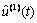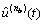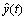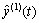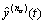，，…，，，，…，，这样就可以得到线性连

由式(10)得最小二乘估计：

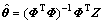。           (11)

3　辨识实例

3.1　仿真算例

3.1.1　二阶模型辨识

设某单输入单输出的线性二阶系统为

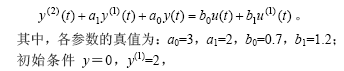
输入信号为u(t)=0.5[1+sin (0.3πt)+cos (0.5πt)]。对式(12)采用四阶龙格-库腾法进行仿真，产生模型输出信号。采样间隔Δt＝0.02 s，总采样时间T＝30 s。为了模拟实际测量情况及检验算法对噪声的抑止能力，在模型输入输出信号中加入高斯白噪声，作为辨识算法的输入输出信号。为了排除计算中随机因素的干扰，以验证本方法的有效性，在每一给定的噪声强度δ下独立施加白噪声，取50次独立辨识结果的平均值作为辨识结果。其中，噪声强度

定义为        。     (13)

定义误差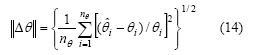     

来表示参数估计的偏差。其中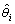：和θ_i分别表示参数

估计值和系统的真实参数；n_θ表示待估计的参数数量。

取频率指数M＝11。图1和图2所示为噪声强度

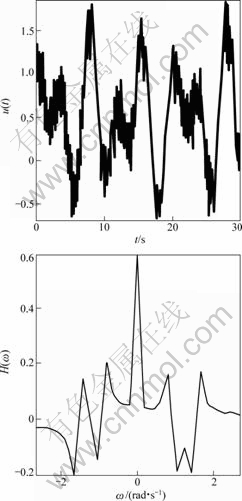
图1　系统输入u(t)及其Hartley谱

Fig.1　System input u(t) and its Hartley spectrum

δ_u=δ_y=30%时仿真系统的输入数据和输出数据及其相应的Hartley谱。图3和图4所示分别为输入信号的一阶、二阶微分信号仿真值及根据Hartley变换与逆变换获得的微分估计值。可以看出，除了时间窗口端点附近的值之外，根据Hartley变换及逆变换得到的一阶、

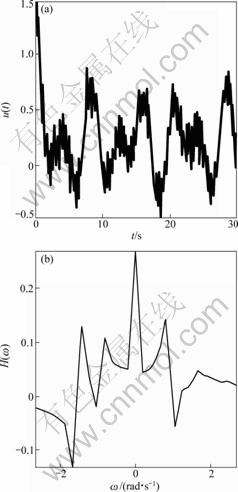
图2　系统仿真输出y(t)及其Hartley谱

Fig.2　Output y(t) and its Hartley spectrum of simulation system

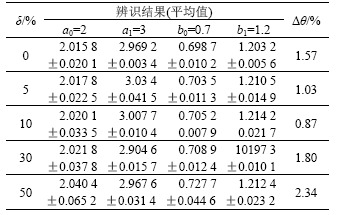
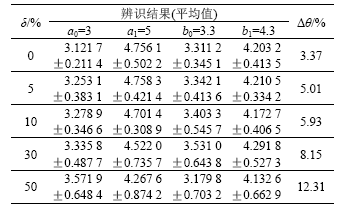
表1　二阶系统参数辨识结果

Table 1　Parameters identification results of two-order system

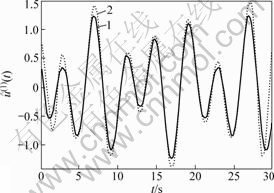
1—真值；2—估计值

图3　仿真系统输入信号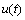的一阶微分及其估计值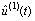

Fig.3　One-order differential of input signal u(t)

and its estimation  of simulation system

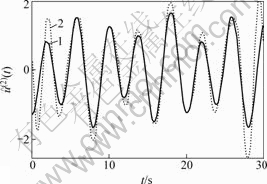
1—真值；2—估计值

图4　仿真系统输入信号的二阶微分及其估计值

Fig.4　Two-order differential of input signal u(t)

and its estimation 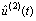 of simulation system

二阶微分估计值比较准确地再现了信号的一阶、二阶微分真值。因信号处理的边界效应，在窗口端点处的值有一定误差。

3.1.2　四阶模型辨识

设一线性四阶系统为

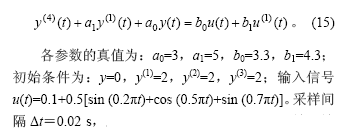
总采样时间T＝20 s，M＝13。输入输出信号获取方式与上述二阶系统的相同。

表2所示为四阶系统辨识结果。可以看出，运用本文方法辨识高阶系统，辨识精度较高，但与低阶系统相比，辨识的精度有所降低，这是利用Hartley变换及反变换获得的高阶微分信号具有较大误差所致。

用上述方法处理输入输出信号，除获得信号的各阶微分外，对含噪声的信号进行了滤波处理，有利于抑制噪声影响。但与此同时，Hartley正、逆变换的近似计算会产生一定的误差。因此，必须注意Hartley谱的频率指数M和时间T的选择。与傅里叶变换相似，

表2　四阶系统参数辨识结果

Table 2　Parameters identification results of four-order system

实际系统中信号的Hartley谱也集中在|mω₀|＜ω_f内(m=0，±1，±2，…，±M；ω_f表示信号的频谱宽度)，而噪声信号的Hartley谱则是近乎均匀地存在于各频率点，因此，在选择合适的M使之包含实际系统频谱的同时，应尽量减少噪声谱的影响。从图5可以看出，无论是否存在噪声，当选择的M在一定范围内时，都能获得比较高的估计精度。试验证明：当M=(3~7)×ω_s/ω₀(ω_s为输入激励信号的频宽)时，辨识精度较高。此外，时间T对系统辨识的精度也有很重要的影响。T必须选择足够大，以保证输入信号能够充分激励系统，同时提高频率分辨力，使之能够充分反映采样数据的频谱成分。

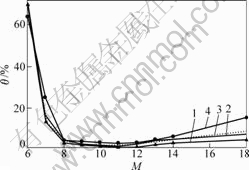
σ/%: 1—0；2—20；3—40；4—80

图5　M对系统辨识精度的影响

Fig.5　The influence of M to identification accuracy of system

3.2　试验辨识实例

为检验算法的有效性，用上述方法对某平整机液压压下系统(Hydraulic Automatic Gage Control, HAGC)进行参数辨识。辨识试验是在国内某大型平整机正常轧制状态下在线进行的^[12]。用文献[12]提供的数据进行参数辨识，在忽略非线性因素及对模型进行简化处理后，HAGC系统可用1/2阶模型描述。

图6和图7所示分别为测试系统用来辨识的某时间段的输入输出数据u(t)和y(t)及根据Hartley变换与逆变换获得的估计值和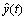。图8~11所示为测试系统的输出值u(t)一阶和二阶微分估计值。

取M＝22，得HAGC系统模型为：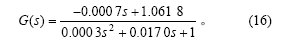

为检验所辨识参数模型的正确性，将上述模型计算的频谱曲线与相关辨识的频谱曲线进行对比。图12所示为幅频和相频的对比曲线。可以看出，在系统有效频率范围内，所辨识的参数模型频谱曲线与相关辨识实测曲线拟合良好，高频段为噪声干扰。

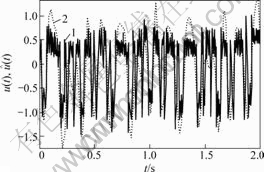
1—真值u(t)；2—估计值

图6　测试系统输入真值u(t)及其估计值

Fig.6　True value u(t) and its estimation of the tested

system input

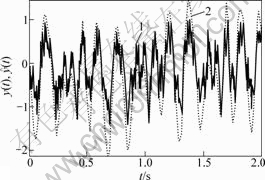
1—真值y(t)；2—估计值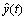

图7　测试系统输出真值y(t)及其估计值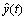

Fig.7　True value y(t) and its estimation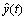

of the tested system output

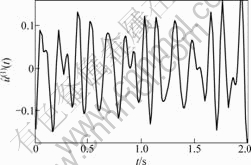
图8　测试系统输入信号u(t)的一阶微分估计值

Fig.8　Estimation of one-order differential of

input signal u(t) of the tested system

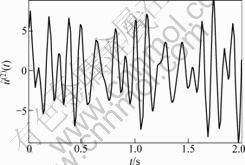
图9　测试系统输入信号u(t)的二阶微分估计值

Fig.9　Estimation of two-order differential of input signal u(t) of the tested system

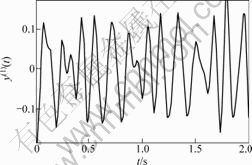
图10　测试系统输出信号y(t)的一阶微分估计值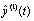

Fig.10　Estimation of one-order differential of

output signal y(t) of the tested system

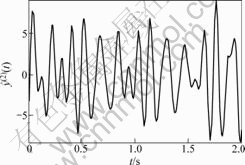
图11　测试系统输出信号y(t)的二阶微分估计值

Fig.11　Estimation of two-order differential

of output signal y(t) of the tested system

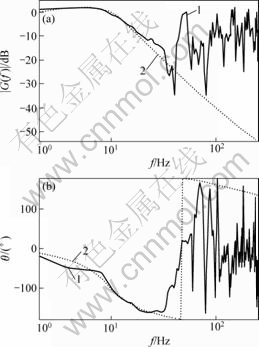
(a) 对数幅频曲线；(b) 对数相频曲线

１—试验辨识结果；2—本文辨识结果

图12　系统频率特性比较

Fig.12　Comparsion of frequency response curves of system

4　结　论

a. 借助Hartley正、逆变换及其微分性质，获取信号微分，避免了微分信号的测量及对含噪信号进行直接处理，用最小二乘算法实现了线性连续动力学模型参数的估计。

b. 研究了频率指数M和时间T对系统辨识精度的影响。仿真及工业试验结果表明，这种辨识方法有较好的噪声抑制能力，有效地避免了直接利用采样数据获取微分信号可能带来的较大误差，同时，Hartley 变换的实变换性也大大提高了计算速度。

参考文献：

[1] Unbehauen H, Rao G. P. A review of identification in continuous-time systems[J]. Annual Review in Control, 1998, 22: 145-171.

[2] Unbehauen H, Rao G P. Identification of continuous systems[M]. Amsterdam: North-Holland, 1987.

[3] Sagara S, Zhao Z Y. Numerical integration approach to on-line identification of continuous time systems[J]. Automatica, 1990, 26(1): 63-74.

[4] Co T B, Ungarala S. Batch scheme recursive parameter estimation of continuous-time systems using the modulating function method[J]. Automatica, 1997, 33(6): 1185-1191.

[5] HE Shang-hong, LI Bing, ZHONG Jue. Continuous-time system identification using Gaussian modulating filters[C]//Proceedings of the 5th World Congress on Intelligent Control and Automation (WCICA04). Hangzhou, 2004: 299-301.

[6] HE Shang-hong, ZHONG Jue. Identification of linear continuous-time system using wavelet modulating filters[J]. Journal of Systems Engineering and Electronics, 2004, 15(3): 270-277.

[7] 贺尚红, 钟　掘. 基于调制函数法的线性连续动力学系统参数模型估计[J]. 机械工程学报, 2003, 39(12): 129-134.

HE Shang-hong, ZHONG Jue. Parameter estimation of linear continuous-time dynamic system using modulating functions method[J]. Chinese Journal of Mechanical Engineering, 2003, 39(12): 129-134.

[8] 张公礼, 潘爱玲. 数字谱方法的理论与应用[M]. 北京: 国防工业出版社, 1992.

ZHANG Gong-li, PAN Ai-ling. The theory and application of digital spectrum method[M]. Beijing: Defense Industry Press, 1992.

[9] Chul H P, Gerard L. Fast hartley transforms for spectral anslysis of ultrasound Doppler signal[J]. IEEE Transaction on Biomedical Engineering, 1988, 35(10): 885-888.

[10] 穆肇骊, 刘　锋, 邱祖廉. 用哈特莱变换估计一类连续非线性系统的参数[J]. 控制理论与应用, 2000, 17(5): 683-688.

MU Zhao-li , LIU Feng, QIU Zu-lian. Parameter estimation of a class of continuous nonlinear systems by Hartley transformation[J]. Control Theory and Applications, 2000, 17(5): 683-688.

[11] Patra A, Unbehauen H. Identification of a class of nonlinear continuous-time systems using Hartley modulating functions[J]. Int J Control, 1995, 62(6): 284-290.

[12] 贺尚红. 连续动力学系统参数模型辨识及工业应用[D]. 长沙: 中南大学机电工程学院, 2002.

HE Shang-hong. Parameter model identification of continuous-time dynamic system and industry application[D]. Changsha: School of Mechanical and Electrical Engineering, Central South University, 2002.

收稿日期：2006-06-15

基金项目：湖南省自然科学基金资助项目(04JJ3029)；湖南省教育厅重点资助项目(05A017)

作者简介：贺尚红(1965-)，男，湖南宁乡人，教授，从事复杂机械系统建模与仿真的研究

通讯作者：陈慧勇，男，博士研究生；电话：13671657324