J. Cent. South Univ. Technol. (2011) 18: 1579-1588

DOI: 10.1007/s11771-011-0875-3

Power system stabilizer design using hybrid multi-objective particle swarm optimization with chaos

Mahdiyeh Eslami¹, Hussain Shareef², Azah Mohamed²

1. Electrical Engineering Department, Islamic Azad University (SRBIAU), Hesarak, Tehran, Iran;

2. Electrical, Electronic and Systems Engineering Department, University Kebangsaan Malaysia,Bangi, 43600, Selangor, Malaysia

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: A novel technique for the optimal tuning of power system stabilizer (PSS) was proposed, by integrating the modified particle swarm optimization (MPSO) with the chaos (MPSOC). Firstly, a modification in the particle swarm optimization (PSO) was made by introducing passive congregation (PC). It helps each swarm member in receiving a multitude of information from other members and thus decreases the possibility of a failed attempt at detection or a meaningless search. Secondly, the MPSO and chaos were hybridized (MPSOC) to improve the global searching capability and prevent the premature convergence due to local minima. The robustness of the proposed PSS tuning technique was verified on a multi-machine power system under different operating conditions. The performance of the proposed MPSOC was compared to the MPSO, PSO and GA through eigenvalue analysis, nonlinear time-domain simulation and statistical tests. Eigenvalue analysis shows acceptable damping of the low-frequency modes and time domain simulations also show that the oscillations of synchronous machines can be rapidly damped for power systems with the proposed PSSs. The results show that the presented algorithm has a faster convergence rate with higher degree of accuracy than the GA, PSO and MPSO.

Key words: passive congregation; chaos; power system stabilizer; penalty function; particle swarm optimization

1 Introduction

With the advent of automatic voltage regulators (AVRs) in the late 1950s, installation of AVRs on power generating units became a common practice. Unfortunately, the high performance of these voltage regulators caused a destabilizing phenomenon on the power system. Most of the problems are associated with the low frequency oscillation in the interconnected power systems, especially in the deregulated paradigm. Small magnitude and low frequency oscillation often remained for a long time [1]. To provide fast damping for the system and thus improve the dynamic performance, a supplementary control signal in the excitation system and/or the governor system of a generating unit can be used. As the most effective damping controller, power system stabilizer (PSS) has been widely applied to suppress the low frequency oscillation and enhance the system dynamic stability. PSSs contribute to maintain the reliable performance of the power system stability by providing an auxiliary signal to the excitation system.

Despite the existence of various structures of PSS, the conventional fixed structure lead-lag PSS (CPSS) is still preferred by most of power utilities. It may be due to the ease of on-line tuning, and the lack of assurance on the stability associated with some variables. To understand the effects of CPSS with different parameters on the overall dynamic performance of the power system, an extensive investigation was done by KUNDUR et al [2]. The investigation illustrated that the satisfactory performance during the system upsets is related to the appropriate choice of the CPSS parameters. The tuning problem of PSS parameters is one of the optimization issues in the power system stability.

Intelligent optimization based methods have been initiated to solve this problem. Two main techniques used for the parameter tuning of PSS in a power system are sequential tuning and simultaneous tuning. The simultaneous tuning of PSS parameters is generally formulated as a very large scale nonlinear non-differentiable optimization problem. This type of optimization problem is very difficult to solve by applying traditional differentiable optimization algorithms. Sequential quadratic programming (SQP) techniques are fast deterministic optimization techniques [3], but they are very sensitive to the choice of initial point. To overcome the problems mentioned above, many random search methods such as genetic algorithm (GA) [4-5], simulated annealing (SA) [6], Tabu search (TS) [7], evolutionary programming (EP) [8] and rule based bacteria foraging [9] have been used. Despite these optimization methods seem to be effective for the design problem, the efficiency is reduced by the use of highly epistatic objective functions, and the large number of parameters to be optimized. Furthermore, they are time consuming methods.

Particle swarm optimization (PSO) was introduced by KENNEDY and EBERHART [10] and it is a kind of random search algorithm that simulates the natural evolutionary process by mimicking the social behavior of flocks (swarms) of birds and insects (particles). Compared with other evolutionary computation algorithms, it has some advantages, including simple implementation, small computational load, and fast convergence. Therefore, it is efficient for solving many problems for which it is difficult to find accurate mathematical models. Despite these advantages, the PSO algorithm is prone to relapse into local minima and premature convergence when solving complex optimization problems.

In order to improve the performance of PSS optimal parameter tuning methods, a modified particle swarm optimization based on the chaos (MPSOC) is proposed in this study. Firstly, passive congregation (PC), which is an important biological force preserving the swarm integrity is introduced in the standard PSO to decease the meaningless search. Secondly, MPSO and chaos are combined to improve the global searching capability and premature convergence to local minima. Then, the problem of tuning of PSS over a wide range of system configurations is formulated as a multi-objective function where the objective is the aggregation of the two objectives related to the damping ratio and damping factor. The proposed optimization procedure handles the problem-specific constraints using a penalty function to enhance the diversity of the swarm, leading to a better outcome. Based on the objective function and the proposed optimization procedure, a multi-machine power system, under a wide range of system configurations and operation conditions, is investigated to verify the effectiveness and robustness of the new method in tuning the PSS parameters.

2 PSO and proposed PSO modifications

2.1 Overview of PSO

Particle swarm optimization (PSO) is a population based stochastic optimization method and a kind of evolutionary computation technique. It explores for the optimal solution from a swarm population of moving particle vectors, based on a fitness function. The method has been found to be robust in solving problems featuring nonlinearity and non-differentiability, multiple optima, and high dimensionality through adaptation, which is derived from the social-psychological theory. Each particle represents a potential answer and has a position  and a velocity  in the problem space. Each particle keeps a record of its individual best position  which is associated with the best fitness it has achieved so far, at any step in the solution. This value is known as the p_best. Moreover, the optimum position between all the particles obtained at the current step in the swarm is stored as global best position  This location is called the g_best. The velocity of particle and its new position will be updated according to the following equations [11]:

                                                       (1)

 i=1, 2, 3, …, N                (2)

where w is an inertia weight that controls the exploration of a particle during a search, c₁ and c₂ are positive numbers explaining the weights of the acceleration terms that guide each particle toward the individual best and the swarm best positions, respectively. r₁ and r₂ are uniformly distributed random numbers in the range of 0-1, and N is the number of particles in the swarm. The inertia weighting function in Eq.(2) is usually calculated using the following equation:

                                         (3)

where w_max is the initial weight, w_min is the final weight, n_I,max is the maximum iteration number, and n_I is the iteration number

The first term in Eq.(2) enables each particle to perform a global search by exploring a new search space. The last two terms in Eq.(2) enable each particle to perform a local search around its individual best position and the swarm best position.

From the PSO equations, it can be revealed that the PSO algorithm does not need a mathematical model of the problem, unlike the traditional optimization algorithms such as Newton’s method. The only information required by the PSO to search for the optimum solution is the evaluation of fitness function.

2.2 Modified particle swarm optimization (MPSO)

In this study, a modified particle swarm optimization (MPSO) is proposed. The MPSO introduces an additional part at the end of the velocity update formula known as the passive congregation part [12]. The basic idea is that individuals need to monitor both their environment and their surroundings. Thus, each group member receives a multitude of information from other members, which may decrease the possibility of a failed attempt at detection or a meaningless search. This kind of information exchange can be realized by a model called passive congregation. The updated velocity equation in MPSO is defined as

           (4)

                                                         (5)

where  is a particle selected randomly from the swarm, c₃ is the passive congregation coefficient, and r₃ is a uniform random sequence in the range of 0-1. It must be noted that each particle obtains passive additional information from another particle that is selected at random. This could increase the diversity of the swarm and lead to a better result.

2.3 MPSO with chaotic sequence (MPSOC)

Chaos is a non-linear phenomenon that widely exists in the nature. Due to the ease of implementation and its special ability to avoid being trapped in local optima, chaos has been a novel optimization technique and chaos-based searching algorithms have aroused intense interests [13]. Chaos phenomenon is different from confusion or erratic behavior. Although it seems like random phenomenon, it is not a real random phenomenon. So, chaos behavior has characteristics of randomness, periodicity, and regularity. Despite of the high efficiency of MPSO, the drawback of premature convergence prevents the algorithm to get the global optimal. To overcome this drawback, chaotic mutation is imposed during the evolution. In this work, the well-known logistic equation [14], which exhibits the sensitive dependence on initial conditions, is employed for constructing hybrid MPSO. The logistic equation used in this work is described as

, k=1, 2, …; θ₀(0, 1)            (6)

where μ is the control parameter with a real value between 0 and 4. Although Eq.(6) is deterministic, it exhibits chaotic dynamics when μ=4 and {0, 0.25, 0.5, 0.75, 1}. That is, it exhibits the sensitive dependence on initial conditions, which is the basic characteristic of chaos. A minute difference in the initial value of the chaotic variable would result in a considerable difference in its long time behavior. The track of chaotic variable can travel ergodically over the whole search space. In general, the above chaotic variable has special characteristics, i.e. ergodicity, pseudo-randomness and irregularity.

To improve the performance of MPSO, a new velocity update equation is introduced by applying chaotic sequence for weight parameter, w, in Eq.(4). The new weight parameter is defined by multiplying Eq.(3) and Eq.(6) in order to improve the global searching capability as

                                                     (7)

It is observed that the proposed new weight decreases and oscillates simultaneously for total iteration, whereas the conventional weight decreases monotonously from w_max to w_min. The difference in the proposed and conventional weight factor is depicted in Fig.1.

Fig.1 Comparison of conventional and new inertia weight

As a result, the updated velocity formula will be assigned according to the following equation:

           (8)

2.4 Constraint optimization using MPSOC

The general constrained nonlinear optimization problem can be defined as

minimize  f(X)

subject to  g_i(X)≤0, i=1, 2, …, p

h_j(X)=0, j=1, 2, …, m

  L_k≤X_k≤U_k, k=1, 2, …, n                             (9)

where X is n-dimensional vector of design variables, f(X) is the objective function, g(X) and h(X) are inequality and equality constraints, and L_k and U_k are lower bound and upper bound constraints.

The MPSOC algorithm requires only the objective function to check whether the new particle position is more favorable than the previous one. A number of approaches have been used in the evolutionary computing to execute constraint handling such as the methods that preserve the feasibility of solutions, penalty-based methods and hybrid methods. In this work, the penalty-based method proposed in Ref.[15] is used. In this approach, the constraint optimization problem in Eq.(9) is replaced with the alternative unconstrained problem as

                                       (10)

In Eq.(10), f(X) is the original objective function of the problem in Eq.(9), r is a penalty factor and l is the power of the penalty function. The function q_i(X) is a relative violation function of the constraints and is given as

                         (11)

The parameters r and l are problem dependent, and r should be a suitably large positive constant. In the present study, the values set for r and l are 1 000 and 2, respectively.

3 Adaptation of MPSOC for PSS tuning

To utilize the developed optimization technique in PSS tuning in the power system, the system elements such as generators, excitation system and PSS must be modeled. It also requires a suitable objective function to obtain satisfactory results. The system model and objective function used in PSS parameter tuning in a multi machine power system are elaborated.

3.1 Power system model

In this study, each generator is modeled as a two-axis, six-order model. For all operating conditions, the power system with generators, PSSs, and excitation systems can be modeled by a set of nonlinear differential equations as

                                                              (12)

where  and u are the vector of state variables and the vector of the damping controller output signals, respectively. The vector of state variables include the speed deviation (Δω), rotor angle (Δδ), the d- and q-axis component of stator voltage (E_q, E_d), and the d- and q-axis component of stator flux (ψ_d, ψ_q), respectively.

In the PSS design, the power system is usually linearized in terms of a perturbed value in order to perform the small signal analysis. Therefore, the system in Eq.(12) is linearized around an equilibrium operating point of the power system. Equation (13) describes the linear model of the power system as

                                                             (13)

where A is the power system state matrix, B is the input matrix, C is the output matrix, and D is the feed-forward matrix. The set of linearized systems is then considered to be controlled by a given configuration of controllers defining a set of linear close-loop systems similar to the close loop setup shown in Fig.2. For each of these systems, it is possible to compute the eigenvalues and then their damping. From Eq.(13), the eigenvalues λ_j=σ_j± iω_j of the total system can be evaluated. Then, the damping ratio (ζ_j) of this eigenvalue is defined by

                                                       (14)

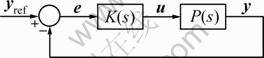
Fig.2 Closed-loop setup

3.2 PSS structure

The operating function of a PSS is to produce a proper torque on the rotor of the machine in such a way that the phase lag between the exciter input and the machine electrical torque is compensated. The supplementary stabilizing signal considered is proportional to the speed. The PSSs with a lead-lag structure of speed deviation input are considered in this study, and the transfer function of the i-th PSS is given by

             (15)

where Δω_i and U_i are the perturbations of the synchronous speed and the output voltage signal respectively, which are added to the excitation system reference perturbation. The signal washout block acts as a high-pass filter with the time constant T_w that allows the signal associated with the oscillations in rotor speed to pass unchanged. Furthermore, it does not allow the steady state changes to modify the terminal voltages. From the view of the washout function, the value of T_w is generally not critical and may be in the range of 0.5-20 s. In this study, it is fixed as 10 s. The phase compensation blocks with time constants T_1i-T_4i supply the suitable phase-lead characteristics to compensate the phase lag between the input and the output signals. The five PSS parameters consisting of the four time constants and the gain need be optimally chosen for each generator to guarantee the optimal system performance under various system configurations and disturbances. The adopted structure of PSS is shown in Fig.3. It consists of a gain block with gain K_i, a signal washout block and two-stage phase compensation blocks. Here, the problem of the robust PSS design is formulated as a multi-objective optimization problem and MPSOC is employed to solve this problem. Furthermore, all the parameters of PSS are considered modifiable. Robustness is obtained by considering some operating conditions and the system configurations simultaneously.

Fig.3 Structure of power system stabilizer

3.3 Objective function

Under an unstable condition, the declining rate of the power system oscillation is determined by the highest real part of the eigenvalue (damping factor) in the power system and the magnitude of each oscillation by its damping ratio. Hence, the objective functions naturally contain the damping ratio and the damping factor in the formulation for the optimal setting of PSS parameters. Therefore, for the optimal tuning of PSS parameters, a multi-objective function may be formulated as

Maximize F₁=min(abs(σ_k))                                        (16)

Maximize F₂=min(ζ_k)                                                 (17)

Minimize

(18)

The design problem can be formulated as the following constrained optimization problem:

Subject to

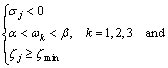
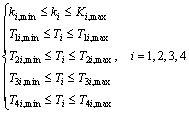                    (19)

where k represents the number of electromechanical modes of oscillation and j=1, 2, 3, …, n. n is the    total number of eigenvalues. σ_k is the real part of the k-th

electro-mechanical mode, and  is

the damping ratio of the k-th electro-mechanical mode. ζ_min is considered experimentally as 0.2. Figure 4 shows the expected performance of the multi-objective function f. It is observed that all the oscillation modes can be relocated by the above multi-objective function. α and β are empirically considered limits of frequency for the electro-mechanical modes. v is a weight for combining both damping factor and damping ratio. The constraint set is made up of bounds of PSS parameters, which can be formulated as Eq.(19). According to Eq.(19), a total of 46+2n inequality constraints should be considered in the optimization of the PSS parameters. Finally, the main objective function may be obtained by substituting the objective function of Eq.(18) and inequality constraints presented in Eq.(19), into Eq.(10). Therefore, the final objective function (fitness function) for optimal tuning of PSS using MPSOC can be formulated as unconstrained objective function in the following form:

                      (20)

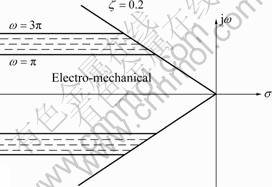
Fig.4 Region of eigenvalue location for objective function F

The implementation procedure of the proposed MPSOC for the optimal design of PSS parameters is shown as a flowchart in Fig.5. The flowchart is self-explanatory, as each single part of the algorithm has been already discussed in previous sections.

4 Simulation results

To demonstrate the application and robustness of MPSOC in tuning of PSS, a two-area multi-machine power system is simulated. The single line diagram of the system is shown in Fig.6. Details of the network parameters are given in Ref.[16]. In this system, there are two generation areas and two loads interconnected by transmission lines. Each area has two generators. All the generators are equipped with identical speed governors and turbines, which include exciters, AVRs and PSSs. The generators and their controls are assumed to be identical. The system is quite heavily stressed, and it has 400 MW flowing on the tie-lines from Area 1 to Area 2. The simple model shows the fundamental electromechanical oscillations that are inherent in interconnected power systems. There are three different electromechanical modes of oscillation, which include two local modes of oscillation corresponding to each area, and one inter-area mode. To analyze the low frequency oscillations in the system, the cases listed in Table 1 representing various operating conditions are studied.

Fig.5 Flowchart of MPSOC used for optimization of PSS parameters

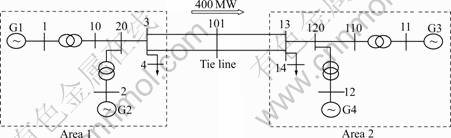
Fig.6 Single line diagram of two area system

Table 1 Cases considered in tuning procedure

4.1 PSS tuning results

The result of the proposed PSS tuning method is compared with the result of GA, PSO and MPSO. The optimization procedure following the methods described above was carried out by a specially prepared computer program coded in MATLAB. All the programs were executed on a 2.10 GHz Pentium IV processor with 2 GB of random access memory (RAM). To achieve the optimum performance in the proposed methodology, the MPSOC parameters need to be carefully adjusted. Table 2 lists the specified parameters for the four algorithms GA, PSO, MPSO and MPSOC used in this study in order to achieve the optimum performance. Furthermore, the conditions listed in Table 2 are also individually studied without any PSS and with CPSS. The parameters used for CPSS are 10.00, 0.05 s, 0.015 s, 0.05 s, and 0.01 s, for K, T₁, T₂, T₃ and T₄, respectively, for all four generators.

The optimal tuning of five PSS parameters, namely K_i, T_1i-T_4i, is performed by the MPSOC. Since there are four PSSs, twenty parameters need be optimized. Fortunately, these parameters have upper and lower limits as listed in Table 3. These limits help in reducing the computational times significantly. In this work, the values of α and β are considered as π and 3π, respectively. The weight parameter v is set to be 10, which is derived from the experiences of many experiments conducted on this problem. First, the system is run without PSS for the four cases mentioned before. Then, PSSs are connected to all the four generators and GA, PSO, MPSO and the MPSOC algorithms are used separately to find out the optimum parameters for the PSSs.

Table 2 Parameters used for GA, PSO, MPSO and MPSOC algorithm

Table 3 Lower and upper limits of PSS parameters

4.1.1 Eigenvalue analysis

The principal eigenvalues and the damping ratios obtained for all operating conditions with no PSS, CPSS and after application of various optimization methods in the system are given in Table 4. The values represent the smallest damping ratio and the unstable cases, respectively. For the system without PSS, it can be observed that some of the modes are weekly damped and for some operating conditions the system is unstable. The addition of PSSs improves the damping in the system oscillations. The results clearly show that the performance of MPSOC optimized PSSs is better than those of MPSO, PSO and GA optimized PSSs, and CPSS. The results from the MPSO show that the minimum damping ratio and the maximum damping factor under all cases are better than those obtained by the use of CPSS, GA and PSO. This means that the addition of passive congregation part can increase the system dynamic stability. Moreover, the results from the MPSOC are better than those from MPSO. This shows that using chaotic sequence in MPSO is an effective approach to enhance the global searching capability and improve the performance stability.

Table 4 Eigenvalues and damping ratios with and without PSSs for four cases

4.1.2 Nonlinear time-domain simulation

A number of time domain simulations were performed to demonstrate the efficiency of tuning of PSS parameters using the proposed MPSOC method. In these tests, to evaluate the effectiveness of the MPSOC based tuned PSS using the proposed multi-objective function, a 200 ms three-phase fault is applied at bus 3 and a fault between the bus 3 and bus 101 is cleared in 0.05 s at the near end. After a further 0.05 s, remote end circuit breaker at bus 101 is operated for the complete clearance in each case. The speed deviations of generators G₁, G₂, G₃ and G₄ under the fault at bus 3 are shown in Fig.7. These time domain simulations are also in good agreement with the results of eigenvalue analysis. The addition of PSSs improves the damping in the system oscillations. It can be seen that the PSSs tuned by the proposed method achieve good results and provide superior damping in comparison with the case when GA, PSO and MPSO are used. All of these figures represent large signal stability of the test systems with optimum PSSs. It is clear that the newly proposed method is quite efficient to damp out the local modes as well as the inter-area modes of oscillations. This illustrates the potential and the superiority of the proposed design approach to get the optimal set of PSS parameters.

4.1.3 Non parametric statistical analysis

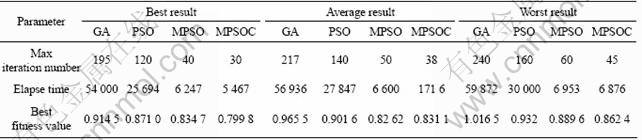
Table 5 presents a comparison of the results obtained by MPSOC, MPSO, PSO and GA in terms of the number of iterations, elapse time and best fitness value achieved by different methods. In order to make a fair comparison among all the three algorithms, the same number of iterations and same ranges of parameters are used. To compare the accuracies of the algorithms, a maximum number of iteration is considered as a stopping condition and the results obtained from the algorithms are compared. The best fitness value achieved by each algorithm is a measure of the strength of the algorithm. Each algorithm was executed for 30 times, and the average elapsed time is considered as a measure of the computational time. As can be seen in Table 5, the best fitness value obtained by MPSOC is 0.799 8 and is slightly lower than the values obtained by MPSO  (0.834 7), PSO (0.871 0) and GA (0.914 5). Also, it is obvious that the proposed algorithm requires far fewer iterations and less computational time when compared with other algorithms. Hence, it can be concluded that the MPSOC is the best among the aforementioned algorithms in terms of accuracy and convergence speed.

Fig.7 Speed response of generators: (a) G1; (b) G2; (c) G3; (d) G4

Table 5 Iterations and time required by GA, PSO, MPSO and MPSOC algorithms

To further validate the reliability of the results, non parametric statistical analysis of the data obtained from 30 independent runs is carried out using SPSS statistic software. First, one-sample Kolmogorov– Smirnov test is conducted in which the null hypothesis, H₀, assumes that the data sample fits normal distribution, and the alternative hypothesis, H₁, assumes that the data sample does not fit normal distribution, with 0.05 significance level. The analysis results are listed in Table 6. As derived from Table 6, the p-value of each algorithm is greater than 0.05, which is not significant enough to reject H₀, and implies that H₁ does not hold true. The p-value is an index which measures the significance of the statistical test. Therefore, this study has 95% confidence that the four sets of test data match normal distribution. After proving that the test data match normal distribution, this research uses paired t-test, to validate each algorithm separately, and to determine the differences of the test data. The results are shown in Table 7. The H₀ of this distribution assumes that the means of the data sets are equal and H₁ assumes that the means of the data sets are not equal. As seen from the Table 7, the pairs with the p-value = 0 are all smaller than 0.05, and the result shows a significant level to reject H₀. This study thus has 95% confidence that the six pairs are significantly different. From Table 7, it can be seen that the MPSOC test results are smaller than other algorithms. In addition, the MPSO test results are better than PSO, from 30 tests. The standard deviations of the three algorithms presented in Table 5 indicate their significant differences. According to Table 5, the standard deviations obtained by MPSOC are smaller than those of the other algorithms and as a result, MPSOC is more stable.

Table 6 Single-sample Kolmogorov-Smirnov test results

Table 7 Paired t-test results

5 Conclusions

1) A new hybrid and modified particle swarm optimization with chaos (MPSOC) is applied for PSSs design in a multi-machine power system. It is done by introducing passive congregation and chaotic sequence into the PSO to decrease a meaningless search and to improve the global searching capability and escape the premature convergence to local minima, respectively.

2) The problem of tuning of PSS over a wide range of system configurations is formulated as a multi- objective function where the objective is the aggregation of the two objectives on the damping ratio and damping factor.

3) A multi-machine power system, under a wide range of system configurations and operation conditions, is investigated to verify the effectiveness and robustness of the new method.

4) The eigenvalue analysis shows acceptable damping of system modes, particularly the low- frequency modes, when the PSSs are tuned by MPSOC. Time domain simulations also show that the oscillations of synchronous machines can be rapidly damped for power systems with the proposed PSSs over a wide range of conditions. Besides, the comparative performances of four optimization algorithms, namely MPSOC, MPSO, PSO and GA for optimal design of PSS have been presented by non parametric statistical analysis. The results show that the presented algorithm has a faster convergence rate with higher degree of accuracy than the GA, PSO and MPSO. The obtained results show that the proposed technique can find the best PSS parameters simultaneously with an excellent global damping performance. Therefore, it is suitable for large scale power systems stability improvement.

References

[1] BASLER M J, SCHAEFER R C. Understanding power system stability [J]. IEEE Transactions on Industry Applications, 2008, 44(2): 463-474.

[2] KUNDUR P, KLEIN M, ROGERS G, ZYWNO M S. Application of power system stabilizers for enhancement of overall system stability [J]. IEEE Transactions on Power Systems, 2002, 4(2): 614-626.

[3] CAI L, ERLICH I. Simultaneous coordinated tuning of PSS and FACTS damping controllers in large power systems [J]. IEEE Transactions on Power Systems, 2005, 20(1): 294-300.

[4] ABDEL-MAGID Y L, ABIDO M A. Optimal multi-objective design of robust power system stabilizers using genetic algorithms [J]. IEEE Transactions on Power Systems, 2003, 18(3): 1125-1132.

[5] SEBAA K, BOUDOUR M. Optimal locations and tuning of robust power system stabilizer using genetic algorithms [J]. Electric Power Systems Research, 2009, 79(2): 406-416.

[6] ABIDO M A. Robust design of multimachine power system stabilizers using simulated annealing [J]. IEEE Transactions on Energy Conversion, 2002, 15(3): 297-304.

[7] ABIDO M A. A novel approach to conventional power system stabilizer design using tabu search [J]. International Journal of Electrical Power & Energy Systems, 1999, 21(6): 443-454.

[8] ABIDO M A, ABDEL-MAGID Y L. Optimal design of power system stabilizers using evolutionary programming [J]. IEEE Transactions on Energy Conversion, 2002, 17(4): 429-436.

[9] MISHRA S, TRIPATHY M, NANDA J. Multi-machine power system stabilizer design by rule based bacteria foraging [J]. Electric Power Systems Research, 2007, 77(12): 1595-1607.

[10] KENNEDY J, EBERHART R. Particle swarm optimization [C]// IEEE International Conference on Neural Networks. Perth, Australia. IEEE Service Center, Piscataway, 1995: 1942-1948.

[11] SHI Y, EBERHART R. A modified particle swarm optimizer [C]// IEEE International Conference on World Congress on on Computational Intelligence, Anchorage, AK, USA. 1998: 69-73.

[12] HE S, WU Q, WEN J Y, SAUNDERS J R, PATON R C. A particle swarm optimizer with passive congregation [J]. Biosystems, 2004, 78(1/2/3): 135-147.

[13] LI Y, ZHANG N, LI C. Support vector machine forecasting method improved by chaotic particle swarm optimization and its application [J]. Journal of Central South University of Technology, 2009, 16(3): 478-481.

[14] WANG Y, ZHOU J, QIN H, LU Y. Improved chaotic particle swarm optimization algorithm for dynamic economic dispatch problem with valve-point effects [J]. Energy Conversion and Management, 2010, 51(12): 2893-2900.

[15] PARSOPOULOS K E, VRAHATIS M N. Particle swarm optimization method for constrained optimization problems [M]. Amsterdam: IOS Press, 2002: 20-55.

[16] ROGERS G. Power System Oscillations [M]. Boston: Kluwer Academic, 2000: 1-7.

(Edited by YANG Bing)

Received date: 2010-11-30; Accepted date: 2011-04-16

Corresponding author: Mahdiyeh Eslami, Tel: +60-173274391; E-mail: mahdiyeh_eslami@yahoo.com