脉冲熔化极气体保护焊的弧长和熔滴尺寸控制

张涛，桂卫华，王随平

(中南大学 信息科学与工程学院，湖南 长沙，410083)

摘要：采用直接模型参考自适应控制算法对弧长和决定熔滴尺寸的焊接电流进行解耦控制，通过调节焊接电源输出电压和送丝速度，使焊接过程中电流和弧长保持在设定值上，使得每个脉冲周期熔化的焊丝体积相等，保证每个周期中熔滴尺寸在脉冲产生之前均匀一致。仿真结果显示该算法可以实现控制对象的输出跟随参考模型的输出。

关键词：脉冲熔化极气体保护焊；解耦控制；弧长和熔滴尺寸控制

中图分类号：TG431.5         文献标志码：A         文章编号：1672-7207(2012)01-0215-06

Control of arc length and size of droplet in pulsed gas metal arc welding process

ZHANG Tao, GUI Wei-hua, WANG Sui-ping

(School of Information Science and Engineering, Central South of University, Changsha 410083, China)

Abstract: A direct model reference adaptive control algorithm was applied to decouple the arc length and the welding current, which were controlled by open circuit voltage and wire feed speed to trace the output of the reference model. The results of simulation show the validity of the control method.

Key words: pulsed gas metal arc welding; decouple control; control of arc length and size of droplet
 

脉冲熔化极气体保护焊(GMAW-P)具有熔滴过渡可控，达到喷射过渡的平均电流低，对母材的热输入量容易控制等优点，适合各种金属材料和各种位置工件的焊接，近年来得到广泛应用^[1]。在GMAW-P焊接过程中，维持电弧的稳定燃烧是保证焊接质量的基本条件，控制器必须在电弧受到波动时，具有使其回到稳定工作点的能力^[2]。Amin等^[3]提出的synergic控制法是根据送丝速度调节脉冲参数，使得由平均电流决定的焊丝熔化速度等于送丝速度，从而保持弧长的稳定，该方法的不足之处在于对弧长的扰动无法进行控制；吴开源等^[4]利用焊接过程中的弧长反馈信号，通过调节脉冲参数，将弧长稳定在给定值上；Essers等^[5]在保持单元电流脉冲能量恒定的前提下，对弧压和送丝速度均进行反馈控制，实现一脉一滴的熔滴理想过渡模式，但由于弧压和送丝速度之间存在耦合，调节比较困难。GMAW-P中熔滴的脱离取决于脉冲电流产生的电磁力的作用，为了保证熔滴在脉冲电流期间能顺利脱落且仅脱落一滴，希望在脉冲产生前的熔滴尺寸保持一致^[6]。根据焊丝熔化率模型，熔滴尺寸是与电流平方相关的量，目前的弧长控制法无法满足对熔滴尺寸的控制^[7]。本文作者采用直接模型参考自适应控制算法对弧长和决定熔滴尺寸的焊接电流进行解耦控制，通过调节焊接电源输出电压和送丝速度的大小，使焊接过程中电流和弧长保持在设定值上，保证每个周期中熔滴尺寸在脉冲产生之前均匀一致。

1  弧长和熔滴尺寸控制策略

目前的熔滴过渡理论主要有静力平衡理论和熔滴收缩不平衡理论。根据熔滴过渡的静力平衡理论，熔滴的过渡是由作用在熔滴上的作用力决定的^[8]，静力包括液态熔滴的重力，保护气体在熔滴周围的流动对液态熔滴产生的拖动力，焊接电流感应磁场作用在熔滴上的电磁力，以及液态熔滴自身的表面张力，当重力、电磁力和拖动力的合力大于表面张力时，熔滴从焊丝上分离进入熔池，熔滴脱落的条件为^[9]：

F_s＜F_g+F_em+F_d              (1)

式中：F_g为重力；F_d为拖动力；F_em为电磁力；F_s为面张力。

在这些作用力中，电磁力F_em是起主要作用的，其大小与焊接电流和熔滴的半径有关，因此在脉冲峰值段，能否保证熔滴顺利脱离，脉冲产生前的熔滴尺寸十分关键。

熔滴收缩不平衡理论将电磁收缩力作为熔滴脱落的主要因素，无限长的液体圆柱在外力的作用下产生波动，其波长的分布趋向于使液柱破断成熔滴。熔滴的过渡也取决于熔滴的尺寸，当熔滴的半径r_d大于临界尺寸r_dc时，熔滴发生脱落，熔滴脱落的临界尺寸  为^[10]：

       (2)

式中：r_d为熔滴半径；r_e为焊丝半径；x_d为熔滴位移；σ为表面张力系数；μ₀为真空导磁率。

目前的GMAW-P弧长控制策略主要是通过调节基值段电流调节或基值段时间来保证弧长稳定。图1所示为弧长的基值电流调节法。图1中，在给定的送丝速度条件下，脉冲峰值电流、脉冲峰值时间和脉冲频率为固定值，在脉冲基值段对弧长进行控制，在脉冲峰值段则不对弧长进行控制，由于脉冲峰值段电流很大，因此脉冲峰值段的弧长要大于基值段。由于弧长控制的影响，基值段的电流值是变化的，因此焊丝在基值段的熔化率也是变化的，在每个周期中，熔滴的尺寸在脉冲到来之前是不一致的。图2所示为弧长的基值时间调节法。图2中，在给定的送丝速度条件下，脉冲基值电流、脉冲峰值电流和脉冲峰值时间为固定值，弧长控制通过调节基值电流段的持续时间来实现，弧长为一个脉冲周期的平均弧长，基值段持续时间在上一个周期结束后由控制器经过计算后得到。由于基值段持续时间是变化的，因此熔滴的尺寸在脉冲产生之前也不是均匀一致的。

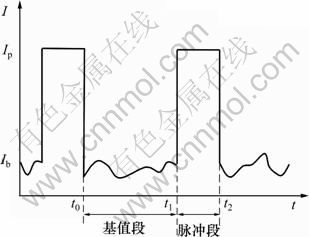
图1  弧长的基值电流调节法

Fig.1  Arc length control via base-current adjustment

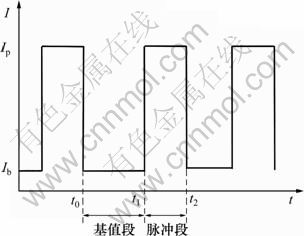
图2  弧长的基值时间调节法

Fig.2  Arc length control via base-period adjustment

由于熔滴尺寸不一致，为了保证各种尺寸的熔滴都能在脉冲期间脱落，因此脉冲峰值时间必须留有充分的余量，这样，对熔滴尺寸较小的熔滴，在促使熔滴过渡的脉冲期间，存在过渡多滴的可能。为了保证GMAW-P中熔滴过渡一脉一滴的理想模式，必须确保在脉冲产生前熔滴的尺寸一致。

焊丝的熔化速度v_m可以表示为^[11]：

               (3)

式中：k₁和k₂为熔化速度常数；l_s为焊丝干伸长。

因为焊丝熔化的体积与熔滴的体积相等，假设熔滴在增长过程中一直保持球形，则下面等式成立：

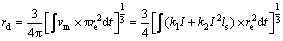 (4)

因此只要在基值段保持弧长稳定的同时能保持基值段电流的稳定，则可以在每个脉冲周期中，在脉冲产生前保持统一的熔滴尺寸。但由于焊接电流和弧长之间存在耦合作用，给控制带来困难。在直接参考模型自适应算法中，控制对象的输出跟随参考模型输出，参考模型可以选择为比控制对象低阶的模型，因此控制器具有结构简单，并且几乎与被控对象无关的特  点^[12]。在GMAW-P弧长和熔滴尺寸控制中，将参考模型选择为无耦合的低阶模型，则可以实现对电流和弧长的解耦控制。通过同时调节焊接电源输出端电压和送丝速度，使得焊接电流和弧长稳定在给定值上，脉冲基值电流，脉冲基值电流时间，脉冲峰值电流和脉冲峰值时间均为固定值，这样，每个脉冲周期熔化的焊丝体积是相等的，可以保证在脉冲到来时熔滴的尺寸是均匀一致的。

2  弧长和电流的解耦控制算法

GMAW-P的焊接过程可用状态空间方程表示  为^[13]：

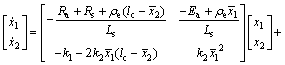
             (5)

式中：x₁为焊接电流；x₂为弧长；R_s为焊接回路输出电阻；R_a为电弧等效电阻；ρ_e为焊丝电阻率；l_c为导电嘴到工件的距离；E_a为弧长因子；L_s为焊接电源输出电感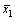；和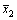分别为状态变量电流和弧长的工作稳态值；系统的输出量y₁和y₂分别为焊接电流和弧长；控制输入量u₁和u₂分别为焊接电源输出电压和送丝速度。

这是一个双入双出的耦合系统，根据GMAW-P的状态空间方程(5)，可以得到其传递函数为：

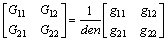        (6)

式中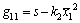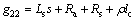：；； ；；den为传递函数分母多项式。

G_p(s)的行列式为：

               (7)

由于传递函数行列式的分子为常数，因此系统是最小相位，分子分母的相对阶数为2，CB＞0，系统的高频增益矩阵是正定的，因此系统是几乎严格正实(ASPR)的，可以采用直接模型参考自适应控制算   法^[14]。

弧长和电流的直接模型参考自适应解耦控制算法结构如图3所示。图3中，y_p(k)，x_p(k)和u_p(k)分别为被控对象的输出向量、状态向量和控制向量，A_p，B_p和C_p为控制对象的具有相应维数的定常矩阵；y_m(k)，x_m(k)和u_m(k)分别为参考模型的输出向量、状态向量和输入向量，A_m，B_m和C_m为参考模型的具有相应维数的定常矩阵。根据正实性理论，离散时间系统的严格正实性要求对象必须存在直接传输项，因此在离散时间系统的直接参考模型自适应算法中引入并联前馈补偿环节D_p，如果G(z)是ASPR的，则扩展系统G_c(z)=G(z)+D_p也是ASPR的^[15]。定义辅助系统输出为：

  (8)

扩展系统和扩展参考模型的输出误差为：

       (9)

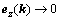因此，只要，则。

自适应控制律为：

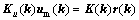        (10)

式中：

        (11)

     (12)

增益矩阵采用PI型自适应律在线调整：

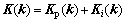             (13)

         (14)

    (15)

图3  离散时间系统直接模型参考自适应解耦算法结构图

Fig.3  Diagram of discrete time direct adaptive control algorithm

3  GMAW-P弧长和电流控制器的  设计

3.1  系统结构

GMAW-P的弧长和电流直接模型参考自适应解耦控制器结构如图4所示。图4中，I_d和l_arcd分别为焊接电流和电弧长度的给定值；I_p和l_arcp分别为实际测量值；e_y1和e_y2分别为焊接电流和电弧电压的跟踪误差；自适应控制器输出向量u_p为电源输出电压和送丝速度。

图4  GMAW-P直接模型参考自适应解耦控制器结构框图

Fig.4  Diagram of discrete time direct adaptive control algorithm for GMAW-P

3.2  直接模型参考自适应解耦控制器的设计

在直接自适应控制算法中，将参考模型选择为无耦合的低阶模型，其传递函数矩阵为：

      (16)

取采样周期T=0.001 s, 其状态方程形式为：

      (17)

自适应算法的参数为：

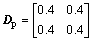
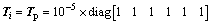    (18)

3.3  仿真研究

按图4的系统结构，以GMAW-P焊接过程为对象进行仿真研究。仿真中设定基值段弧长的给定值为1 mm，基值段焊接电流为50 A，峰值段弧长的给定值为11 mm，脉冲电流为380 A。图5和图6所示分别为参考模型的时间常数等于0.001时焊接电流和电弧长度的仿真结果。图7和图8所示分别为参考模型的时间常数等于0.000 3时焊接电流和电弧长度的仿真结果。从仿真的结果可以看出：一方面直接自适应控制算法的控制输出y_p(k)能很好地跟随参考模型的输出y_m(k)，实现了弧长和电流的独立控制，保证了在焊接过程的弧长稳定的前提下，每个熔滴的尺寸均匀一致，确保了一脉一滴的理想过渡模式的实现；另一方面，控制算法要求焊接电源具有较快的动态特性。

图5  参考模型时间常数为0.001时的GMAW-P焊接电流仿真波形

Fig.5  Simulation of welding current waveform in GMAW-P with time factor of model of 0.001

图6  参考模型时间常数为0.001时的GMAW-P电弧长度仿真波形

Fig.6  Simulation of arc length waveform in GMAW-P with time factor of model of 0.001

图7  参考模型时间常数为0.000 3时的GMAW-P焊接电流仿真波形

Fig.7  Simulation of welding current waveform in GMAW-P with time factor of model of 0.000 3

图8  参考模型时间常数为0.000 3时的GMAW-P电弧长度仿真波形

Fig.8  Simulation of arc length waveform in GMAW-P with time factor of model of 0.000 3

4  结论

(1) 采用弧长和焊接电流的解耦控制，通过同时调节焊接电源输出电压和送丝速度，使得GMAW-P焊接过程中，在保证弧长稳定的同时，保证在脉冲产生前熔滴的尺寸均匀一致。

(2) 直接参考模型自适应算法的参考模型可以选择为比控制对象低阶的模型，控制器具有结构简单，并且几乎与被控对象无关的特点。将参考模型选择为无耦合的低阶模型，则可实现对控制对象状态变量的解耦控制，但该算法要求控制对象为几乎严格正实，使用条件较为苛刻。

(3) Matlab仿真显示系统的输出能很好地跟踪参考模型的输出，验证了算法的有效性。

参考文献：

[1] 李芳, 华学明, 吴毅雄. 脉冲熔化极气体保护焊研究现状与发展[J]. 热加工工艺, 2007, 36(15): 84-87.
LI Fang, HUA Xue-ming, WU Yi-xiong. Situation and development of GMAW-P[J]. Hot Working Technology, 2007, 36(15): 84-87.

[2] Thomsen J S. Control of pulsed gas metal arc welding[J]. International Journal of Modeling, Identification and Control, 2006, 1(2): 115-125.

[3] Amin M, Naseer-Ahmed. Synergic control in MIG welding for power current controllers using a thyristor controlled power source for steady DC open arc operation[J]. Joining & Materials, 1989, 2(1): 13-19.

[4] 吴开源, 黄石生, 李星林, 等. 基于DSP的GMAW-P焊数字化控制系统[J]. 焊接学报, 2008, 28(11): 41-44.
WU Kai-yuan, HUANG Shi-sheng, LI Xing-lin, et al. DSP based digital control system for GMAW-P[J]. Transactions of the China Welding Institution, 2008, 28(11): 41-44.

[5] Essers W G, van Gompel M R M. Arc control with pulsed GMA welding[J]. Welding Journal, 1984, 63(6): 26-32.

[6] Palani P K, Murugan N. Selection of parameters of pulsed current gas metal arc welding[J]. Journal of Materials Processing Technology, 2006, 17(2): 1-10.

[7] 彭海燕, 黄石生, 蒋东. 脉冲MIG焊熔滴过渡控制的发展现状[J]. 焊接技术, 2007, 36(1): 6-9.
PENG Hai-yan, HUANG Shi-sheng, JIANG Dong. The status quo of droplet transfer control of pulsed MIG[J]. Welding Technology, 2007, 36(1): 6-9.

[8] Yudodibroto B Y B, Hermans M J M, Hirata Y, et al. Pendant droplet oscillation during GMAW[J]. Science and Technology of Welding and Joining, 2007, 11(3): 308-314.

[9] Arif N, Lee J H, Yoo C D. Force-displacement model for analysis of pulsed-GMAW[J]. Journal of Physics D: Applied Physics, 2009, 42(3): 504-511.

[10] 武传松, 陈茂爱，李士凯. GMAW焊接熔滴长大和脱离动态过程的数学分析[J]. 机械工程学报, 2006, 42(2): 76-81.
WU Chuan-song, CHEN Mao-ai, LI Shi-kai. Dynamic analysis of droplet growth and detachment in GMAW[J]. Chinese Journal of Mechanical Engineering, 2006, 42(2): 76-81.

[11] Lesnewich A. Control of melting rate and metal transfer in gas shielded metal arc welding: Part Ⅰ[J]. Welding Research Supplement, 1958, 37(8): 343-353.

[12] 李年裕, 刘藻珍. 一种新的直接自适应控制方法及其在制导系统中的应用[J]. 控制理论与应用, 2007, 24(5): 825-828.
LI Nian-yu, LIU Zao-zhen. A new direct adaptive control and its application to a guidance system[J]. Control Theory & Applications, 2007, 24(5): 825-828.

[13] Naidu D S, Ozcelik S. Modeling, sensing and control of gas metal arc welding[J]. Welding Journal, 1993, 72(6): 269-278.

[14] Kaufman H. Direct adaptive control algorithms: Theory and applications[J]. Applied Mechanics Reviews, 1995, 48(6): 74-79.

[15] 尹怡欣, 孙一康. 一种离散时间直接自适应控制算法[J]. 北京科技大学学报, 1999, 21(5): 502-504.
YIN Yi-xin, SUN Yi-kang. A discrete time direct adaptive control algorithm[J]. Journal of University of Science and Technology Beijing, 1999, 21(5): 502-504.

(编辑 杨幼平)

收稿日期：2010-11-22；修回日期：2011-02-24

基金项目：国家高技术研究发展计划(“863”计划)项目(2009AA04Z137)

通信作者：张涛(1969-)，男，湖南长沙人，博士研究生，副教授，从事工业过程控制和智能焊接设备研究；电话：18907315085；E-mail: 3ztp@163.com