DOI： 10.11817/j.issn.1672-7207.2020.04.004

碳纳米管表面缺陷对聚甲基丙烯酸甲酯基体弹性的影响

李云龙¹,杨斌²,唐黎明³,李皓¹,王照智²,刘冬¹

（1. 汕头大学 工学院，广东 汕头，515063；

2. 沈阳工业大学 机械工程学院，辽宁 沈阳，110870；

3. 沈阳化工大学 能源与动力工程学院，辽宁 沈阳，110142）

摘要:碳纳米管(CNTs)及其高分子复合材料在制备过程中，需要经过温度、溶液和力场等的耦合作用。因此，CNTs表面不可避免产生缺陷。为探索缺陷对复合材料弹性性能的影响机理，构建表面含有TSW (thrower-stone-wales)、SV (single vacancy)和无缺陷的CNTs增强聚甲基丙烯酸甲酯(PMMA)基体的分子模型，利用分子动力学理论和恒定应变拉伸法计算高分子纳米复合材料的弹性模量；分别研究在拉伸过程中CNTs与PMMA间的界面作用能和CNTs的弹性性能，揭示CNTs表面缺陷种类和数量对PMMA基体弹性性能的微观影响机理。研究结果表明：相较于无缺陷CNTs，表面含有TSW和SV缺陷的CNTs高分子复合材料的弹性性能均呈现一定程度降低，其中SV缺陷对复合材料基体弹性性能影响最明显；在拉伸过程中，CNTs自身的弹性性能在影响复合材料基体弹性性能中起到主导作用；高分子复合材料的弹性模量均随着CNTs表面缺陷数量增加而逐渐降低。在实际应用中，若要保证高分子复合材料的韧性和抗断裂性能时，可适当增加CNTs表面的缺陷数量，但当要保证确保高分子复合材料的强度时，需要尽量减少CNTs表面缺陷。

关键词:碳纳米管；高分子复合材料；分子模拟；表面缺陷；界面作用

中图分类号:TB 383.1      文献标志码:A          开放科学(资源服务)标识码(OSID)

文章编号:1672-7207（2020）04-0893-09

Effects of defected carbon nanotubes on the elastic properties of polymethyl methacrylate matrix

LI　Yunlong¹, YANG　Bin², TANG　Liming³, LI　Hao¹, WANG　Zhaozhi², LIU　Dong¹

(1. College of Engineering, Shantou University, Shantou 515063, China；

2. School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China；

3. School of Energy and Power Engineering, Shenyang University of Chemical Technology,Shenyang 110142, China)

Abstract: In the preparation of carbon nanotubes(CNTs) and CNTs/polymer composites, the coupling effects of temperature, solution and force field could not be avoided. Therefore, the formation of defects on the surface of CNTs were inevitable. Molecular models of polymethyl methacrylate(PMMA) matrix reinforced by carbon nanotubes(CNTs) containing thrower-stone-wales(TSW), single vacancy(SV) defects on the surfaces were built respectively. Molecular dynamics simulations were conducted to determine the elastic modulus of the CNTs/polymer composites. The interfacial interactions between CNTs and PMMA during the tensile process and the elastic behaviors of CNTs were particularly investigated and analyzed to reveal the atomic inherent mechanisms of the effects of surface defects of CNTs on the elastic properties of PMMA matrix. The results show that the elastic modulus of TSW and SV-CNTs/polymer composites decrease in comparison with that of the pristine CNTs. The elastic modulus of SV-CNTs/polymer composites is lower than that of the TSW-CNTs/polymer composites. During the tensile process, the elastic properties of CNTs have more important effects on decreasing the elastic modulus of the polymer matrix than that of the interfacial interactions between CNTs and polymer matrix. In addition, the elastic modulus of polymer composites deceases with the increase of the number of the defects on the surface of CNTs. When the toughness and fracture resistance of polymer composites are required in practical application, the number of defects on CNTs surface can increase appropriately by certain ways. In contrast, when the strength of polymer composites is required, the occurrence of defects on CNTs surface should be avoided.

Key words: carbon nanotubes; polymer composites; molecular simulation; surface defects; interfacial interaction

碳纳米管(CNTs)因其良好的力学性能、热力学性能和表面吸附活性等优势，被视为理想的纳米补强剂，广泛地应用在高分子复合材料领域^[1-3]。近年来，许多学者研究了CNTs增强高分子复合基体的力学性能。DEPLANCKE 等^[4]探索CNTs的预设分布对超高分子量聚乙烯(UHMWPE)纳米复合材料的力学性能的影响，发现CNTs/UHMWPE复合材料的屈服应力和应变硬化特性可在混入较高的CNTs浓度后得到改善；TARFAOUI等^[5]分别制备了不同体积分数的CNTs纳米织物复合材料，探索了不同体积分数下的CNTs对织物基复合材料基体弹性性能的影响。实验观察到加入的CNTs可有效地控制复合材料试件的损伤萌生和裂纹扩展。同时，织物基复合材料的弹性模量可提升2%以上。为深入掌握CNTs/高分子纳米复合材料的结构和力学特性，特别是在探索CNTs与高分子基体间的界面作用方面，基于连续力学的理论探索方法得到了长足发展。ZALAMEA等^[6]利用连续介质力学中的2种方法计算了多壁碳纳米管(MWCNT)结构中多个壳层之间的界面相互作用，并认为MWCNT能有效地将应力从基质传递到其内部；GAO等^[7]提出了由CNTs增强的聚合物复合材料的剪切滞后模型，并使用多尺度方法研究从聚合物基体到CNTs最内层的载荷转移以及影响载荷传递的因素；SPANOS等^[8]应用细观力学混合有限元方法研究了单壁碳纳米管(SWCNT)增强复合材料的应力传递，并详细分析了SWCNT体积分数、界面刚度和基体弹性模量对应力传递的影响。值得注意的是，基于宏观连续力学的理论模型均采取对CNTs的无缺陷结构的连续体假设，但在实际的CNTs/高分子纳米复合材料的制备过程中，通常需要采取如温度、压力和化学处理等复杂的工艺流程处理。由于CNTs自身的sp² 杂化结构具有较好反应活性，目前CNTs表面的缺陷现象是无法避免的^[9]。此时，传统的连续力学理论模型无法捕捉到CNTs自身微观结构的改变，导致很难通过实验以及传统连续力学等手段预测与分析CNTs/高分子纳米复合基体准确的力学性能。分子动力学(MD)是一种有效的计算机模拟方法，用来探究不同环境下分子构象与形态以及分子之间相互作用过程。MD模拟可以有效地捕捉CNTs表面缺陷的微观信息，并同时计算其与高分子之间的相互作用以及高分子纳米复合材料的宏观力学性能。LU等^[10]利用了MD理论，模拟研究了Stone-Wales缺陷对单壁纳米管(SCNT)的力学性能的影响，发现SCNT的断裂总是从缺陷的位置开始发生，而对于无缺陷管，裂纹位置随机产生。对于给定的缺陷数，与扶手式SCNT管相比，锯齿形结构SCNT的平均强度和极限应变相对较小。目前，部分研究利用MD模拟来探索CNTs缺陷对其弹性性能的影响，但含缺陷CNTs/高分子纳米复合材料的MD模拟工作却鲜有报道，其内在原子层面的微观机理仍有待探索与揭示。为此，本文建立了含不同缺陷种类和缺陷数量的CNTs增强高分子复合基体分子模型，利用MD理论模拟了高分子复合材料的弹性模量，通过提取相关的微观参数，重点对比与分析CNTs的表面缺陷种类与数量对高分子复合材料弹性模量的内在微观影响机理，为工程实际提供微观理论支撑。

1 分子建模与动力学模拟

为探索表面含缺陷的CNTs对高分子纳米复合基体弹性模量的微观影响机理，建立含不同缺陷种类和数量的CNTs增强高分子复合基体分子无定型模型。

第1步，构建不同种类CNTs分子结构，直径为10.85 nm，长度为59.03 nm的非缺陷(8，8) CNTs为碳管的基础构型。图1所示为表面含缺陷的CNTs模型，选定与构建thrower-stone-wales(TSW)和single vacancy(SV)这2种实验中常见的缺陷类型下的CNTs分子结构^[11-12] ，分别如图1(a)和(b)所示。其中，TSW缺陷的构建原理是将C—C键旋转90°后重新组合共价键，原有的4个相邻的六角形环转换成2个相邻的五角形环和2个分离的七角型环。此时，原有CNTs上的sp²结构并未受到任何影响。SV缺陷的成型原理则是将表面1个碳原子删除，由于碳原子的高活性，用氢原子填充余下的不饱和共价键。为探索CNTs表面不同数量缺陷对高分子基体弹性模量的微观影响机理，针对SV和TSW这2种缺陷，分别随机构建了排布有7，14，21和28个缺陷的CNTs，如图1(c)所示。

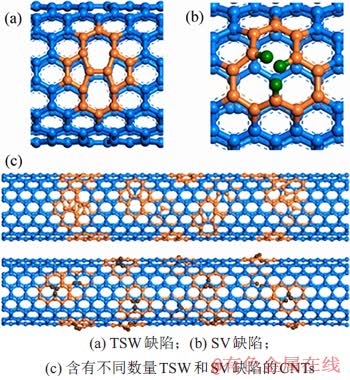
图1　表面含缺陷的CNTs模型

Fig. 1　Molecular models of CNTs with different surface defects

第2步，选取分子式为CH₂=C[CH₃]CO₂CH₃的聚甲基丙烯酸甲酯(PMMA)为高分子材料。采用Materials Studio(MS)分子模拟软件的Visualizer建模模块建立聚合度为5的分子链模型，如图2(a)所示。为构建CNTs/PMMA纳米复合基体，建立带有周期性边界条件且长×宽×高为6.5 nm×5.0 nm×5.0 nm的单元模拟盒子，将CNTs放置盒子中心位置(CNTs长度方向与盒子长度方向一致)，如图2(b)所示。然后利用Amorphous Cell (AC)模块，基于蒙特卡罗“随机数”的计算方法，将建立的分子链随机填充到含有CNTs的周期性单元盒子，直至填充密度达到1.10 g/cm^3[13]。依照此方法，分别拓展建立全部种类CNTs/PMMA的无定型高分子复合材料模型，如图2(c)所示。

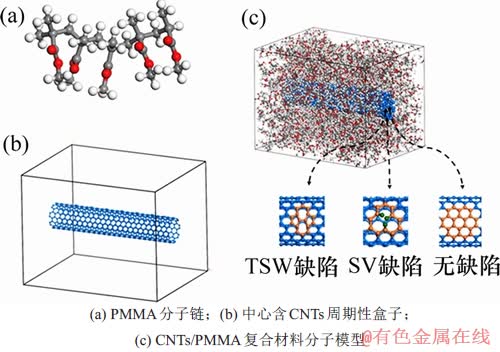
图2　CNTs/PMMA 复合材料模型

Fig. 2　Molecular modeling process of CNTs/PMMA composites

第3步，为得到局部最优分子构型，对构建的CNTs/PMMA模型进行几何结构优化处理。其中，优化方法选取共轭梯度法^[14]，其能量收敛精度设置为0.418 6 J/mol。为寻找高分子复合基体的全局能量最低构象，对几何优化后的所有模型继续进行NPT系统下的动力学平衡处理，温度设置为298 K，压力设置为1个标准大气压，总模拟时间为2×10^-9 s，模拟步长为1×10^-15 s。在所有建模、优化与动力学模拟过程中，选取COMPASS^[15-18]力场。其中，静电作用能的求解方法为Ewald^[19]，截断半径设置为1.25 nm。选取Andersen^[20]算法控制温度，选取Berendsen算法^[21]控制压力。

2 不同缺陷种类CNTs增强PMMA基体拉伸计算

为探索CNTs表面不同缺陷种类对高分子纳米复合材料弹性模量的影响，首先，构建表面分别含有14个TSW和SV缺陷的CNTs/PMMA和无缺陷CNTs/PMMA的分子无定型复合基体模型；随后，采用恒定应变法(strain-constant method) ^[22]，对3个分子模型进行MD拉伸模拟。拉伸模拟方法如下：以1.0×10^-4为拉伸应变率，在盒子的长度方向均匀扩展晶格尺寸，如图3所示。

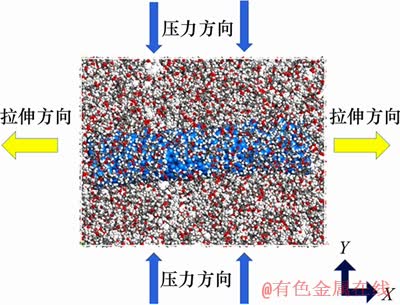
图3　CNTs/PMMA基体MD拉伸方法

Fig. 3　Method of tensile process of CNTs/PMMA composites by MD simulations

其中，每拉伸1步后，分子体系需在NPT系综下(298 K温度；y和z轴方向施加0.1 MPa压力)进行1 ps的动力学平衡，使盒子内所有原子重新适应拉伸后尺寸，再根据式(1)计算模型在每步拉伸中的最后一帧的拉伸方向应力，并记录。所有MD拉伸模拟均通过LAMMPS软件实现^[23]。

维里应力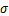在模型的每个增量方向的计算公式如下：

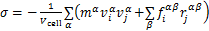(1)

式中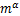：为原子α的质量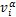；和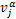分别为原子α在i和j方向的速度分量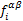；为原子β施加在原子α上的i方向的力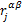；为α和β原子在j方向的距离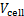；为模型体积。

最后，3个分子模型在线性阶段的应力-应变曲线如图4所示。经计算，无缺陷CNTs/PMMA，TSW-CNTs/PMMA和SV-CNTs/PMMA的弹性模量分别为3.131，2.913和2.696 GPa。由此可知，当CNTs表面存在TSW和SV缺陷时，其复合基体的弹性模量均呈现降低趋势，分别降低了6.96%和13.89%。其中，相对于TSW缺陷，含SV缺陷的CNTs/PMMA复合基体的弹性模量更小。

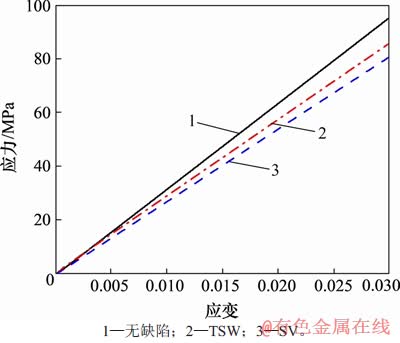
图4　无缺陷CNTs/PMMA，TSW-CNTs/PMMA，SV-CNTs/PMMA的应力-应变曲线

Fig. 4　Strain-stress curves of non-defects CNTs/PMMA, TSW-CNTs/PMMA and SV-CNTs/PMMA composites

3 CNTs不同缺陷种类的影响机理

根据ARASH等^[24]的研究可知：纳米复合材料基体的弹性模量由补强剂的弹性模量和补强剂与高分子基体之间的界面作用共同决定。因此，为探究CNTs的表面缺陷影响复合基体拉伸性能的微观机理，着重对这2个因素进行探索与分析。

3.1　不同缺陷种类CNTs与PMMA基体界面作用能计算与分析

首先根据式(2)，分别提取3种复合材料模型在拉伸过程中CNTs与PMMA基体之间的界面能量变化曲线，如图5所示。由图5可见：在拉伸过程中，表面含有无缺陷、TSW与SV缺陷的CNTs与PMMA基体的界面作用能量的平均值分别为34.95，45.42和40.48 kJ/mol。

(2)

式中：U_Inter为CNTs与PMMA基体之间的界面能量；U_Total为CNTs/PMMA复合基体的总势能；U_PMMA为PMMA基体势能；U_nano为CNTs的势能。

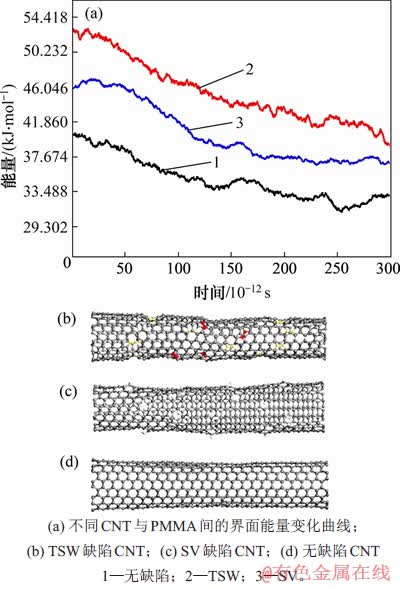
图5　拉伸过程中不同缺陷种类CNTs与高分子基体界面作用能量变化及CNTs自身结构示意图

Fig. 5　Variations of interfacial energy between CNTs and polymer matrix during tensile process and molecular models of different CNTs

由图5可知：当CNTs表面存在TSW和SV缺陷时，在拉伸过程中与PMMA基体的界面相互作用力得到了一定程度提升。这是因为当SV缺陷存在时，由于苯环缺少1个碳原子，其CNTs表面的SP²杂化数量减少，原则上表面吸附力应降低，但由于CNTs未破坏的表面仍有较好吸附活性，同时缺陷处引入的3个氢原子降低了CNTs表面的平滑性，CNTs结构受到一定程度的形变，进而出现了波浪构型与褶皱现象(如图5(c)所示)，因此，在CNTs结构变化和氢原子的综合作用下，SV-CNTs表面对PMMA分子链的吸附力比无缺陷CNTs模型的吸附力提高了15.8%。

而当CNTs表面存在TSW缺陷时，其缺陷并没有破坏CNTs原本的SP²的数量与杂化结构，CNTs表面也因结构的改变出现明显的波浪与褶皱现象(如图5(b)所示)，进而改变了CNTs原有的线性光滑表面特性，同时TSW-CNTs仍保持原有CNTs表面的较强静电吸附作用力，导致PMMA分子链更易于缠绕和吸附在CNTs表面。当复合材料基体被拉伸时，这些表面波浪构型和褶皱现象可阻碍高分子链向拉伸方向移动，从而相比无缺陷CNTs和SV-CNTs，可呈现更高的界面作用能量，可分别提升29.94%和12.20%。

值得注意的是，虽然含TSW与SV缺陷的CNTs与PMMA基体的界面作用能量更高，但TSW和SV-CNTs/PMMA复合基体的弹性模量相对于无缺陷CNTs/PMMA基体的弹性模量却分别降低了7.03%和13.74%。由此可推测TSW和SV-CNT与PMMA之间的界面作用对整体复合材料的拉伸性能影响较小，TSW和SV-CNTs自身的弹性模量对复合材料的弹性模量起到主要作用。

3.2　不同缺陷种类CNTs拉伸计算与分析

为证实以上观点，再对无缺陷CNTs，TSW-CNTs与SV-CNTs这3种碳管单独模拟应变率为1.0×10^-4的分子动力学拉伸，计算并提取其应力应变曲线，如图6所示。根据图6可计算出3种碳纳米管的弹性模量分别为616.6，543.1和469.4 GPa。由此可知：无缺陷CNTs的弹性模量最大，含TSW和含SV缺陷的CNT分别降低了11.92%和23.87%。对于TSW缺陷，其表面结构相对SV缺陷比较完整，但其微观构型仍比无缺陷CNTs的稳定性低；在SV缺陷结构中，因缺少了1个碳原子，原本CNTs的连续苯环结构被打破，缺陷处易诱发应力集中现象，因此，其应力降低，弹性模量最低。

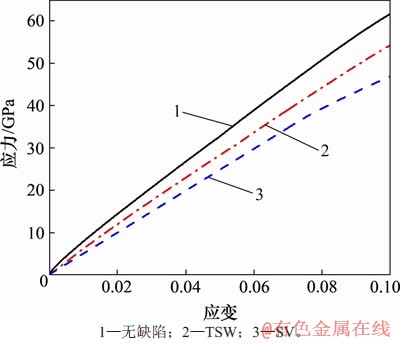
图6　无缺陷CNTs，TSW-CNTs与SV-CNTs的应力-应变曲线

Fig. 6　Strain-stress curves of non-defects CNTs, TSW-CNTs and SV-CNTs

通过对CNTs与PMMA之间的界面能量与单独CNTs弹性模量的综合分析和比对可知，对于TSW和SV-CNTs/PMMA复合基体，虽然含缺陷CNTs与PMMA基体的界面作用能要比无缺陷CNTs模型的界面作用略高，但TSW和SV-CNTs的弹性模量相对于无缺陷CNT的弹性模量分别降低了11.92%和23.87%。显而易见，此时TSW和SV-CNTs自身的弹性模量在影响复合基体的弹性模量中占据主导作用，导致高分子基体的弹性模量最终呈降低趋势。同时，由于TSW-CNTs的弹性模量要高于SV-CNTs的弹性模量15.7%，因此，TSW-CNTs/PMMA复合基体的弹性模量高于SV-CNTs/PMMA复合基体的弹性模量。

4 不同缺陷数量CNTs增强PMMA基体拉伸计算

为进一步探索CNTs表面缺陷数量对高分子复合基体拉伸性能的影响，利用MD模拟方法，分别计算表面含有7，14，21和28个TSW和SV缺陷的CNTs/PMMA复合基体分子模型的拉伸行为，其应力-应变曲线如图7所示。由图7可见：表面含有7，14，21和28个TSW复合材料基体的弹性模量分别为3.017，2.913，2.622和2.533 GPa，表面含有7，14，21和28个SV-CNTs/PMMA复合材料基体的弹性模量分别为2.781，2.696，2.412和2.387 GPa。含有2种缺陷类型的CNTs/高分子基体均呈现出随着缺陷数量增加而弹性模量减少的趋势。

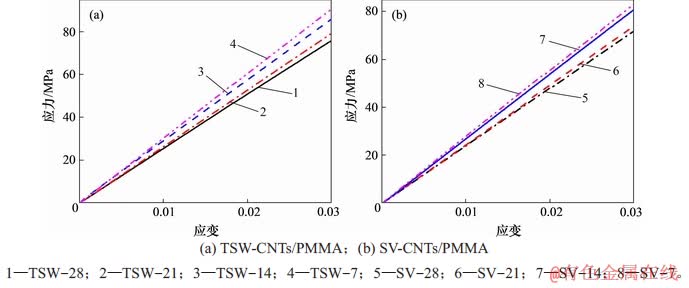
图7　不同缺陷种类与缺陷数量下复合材料基体的应力-应变曲线

Fig. 7　Strain-stress curves of PMMA matrix reinforced by different defected CNTs and different defects numbers

5 CNTs不同缺陷数量的影响机理

5.1　不同缺陷数量CNTs与PMMA基体界面作用能计算与分析

首先，根据式(2)，计算并提取了MD拉伸模拟过程中，所有模型内TSW和SV-CNTs与PMMA之间的界面作用能量，如图8所示。

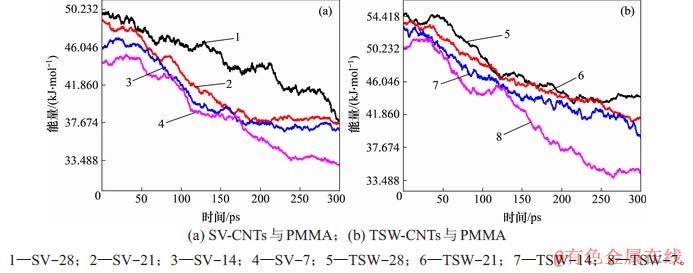
图8　含不同缺陷数量的CNTs与PMMA界面作用能

Fig. 8　Variations of interfacial energy between PMMA matrix and CNTs with different defects number

由图8可见：随着缺陷数量增加，TSW-CNT与PMMA界面间的作用能平均值在缺陷数量为7，14，21和28时分别为41.990，45.422，46.758和47.783 kJ/mol，SV-CNT与PMMA界面间作用能平均值在缺陷数量为7，14，21和28时分别为38.670，40.483，41.542和44.770 kJ/mol。根据此前分析的结论，随着缺陷数量增加，CNTs本身的构型越发不规则，表面的褶皱和波浪特征逐渐增加，导致在拉伸过程中，CNTs表面吸附周围PMMA分子链，提升了界面间的作用力。在相同缺陷数量的情况下，TSW-CNTs比SV-CNTs与PMMA基体之间的界面能相对要高。这是由于引入SV缺陷，虽然可引入更多的氢原子，但CNTs表面的sp²杂化结构受到损坏，杂化结构的数量随着缺陷增加逐渐减少，而引入TSW缺陷并没有改变sp²杂化结构和数量，保持着CNTs本身较强的吸附力，同时，其表面的褶皱和波浪特性也随着缺陷数量增加而增强，因此，TSW-CNTs与PMMA基体之间的界面作用逐渐增加。

5.2　不同缺陷数量CNTs拉伸计算与分析

含有不同缺陷数量下单独TSW和SV-CNTs的应力-应变曲线如图9所示。从图9可见：随着缺陷数量由7增加到28，TSW-CNTs的弹性模量逐渐由578.73 GPa减少到461.60 GPa；SV-CNTs的弹性模量逐渐由524.56 GPa减少到320.21 GPa。对于2种缺陷下的CNTs，其弹性模量均随缺陷数量增加而减少，这是因为随着缺陷数量增加，其结构越发不稳定，应力集中现象增多，进而碳管本身承受拉伸能力逐渐降低。

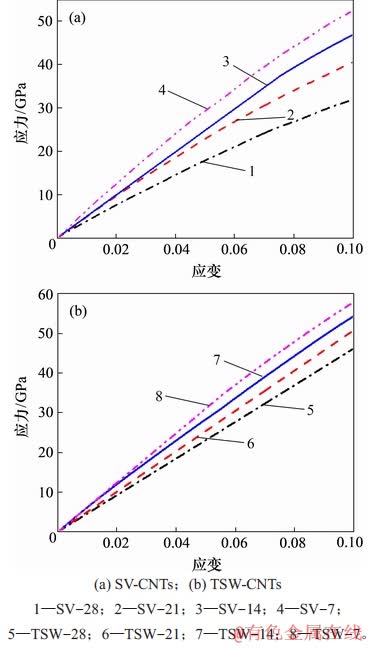
图9　不同缺陷数量下CNTs的应力-应变曲线

Fig. 9　Strain-stress curves of TSW-CNTs and SV-CNTs with different defects number

由以上计算结果可知：CNTs自身的弹性模量在影响复合材料基体的弹性模量方面占据主动作用，这与此前的结论相一致。同时，由于随缺陷数量增加，CNTs的弹性模量逐渐降低，导致CNTs增强复合材料基体的弹性模量也随着CNTs表面缺陷数量降低而降低。

在含有相同缺陷数量的情况下，SV-CNTs的弹性模量要比TSW-CNTs的小。该现象可解释为：对于SV缺陷，由于碳管表面碳六边形结构被破坏，结构不连续特性相对更明显，SV-CNTs结构承载外力能力比TSW-CNTs更低，因此，由于CNTs的主导作用，相对于SV-CNTs，在相同缺陷数量下TSW-CNTs增强高分子复合基体的弹性模量更大。

由文献[13]可知，当纳米补强材料有具有较高的界面作用力时，可有效提升高分子基体的韧性和抗断裂性能。因此，在实际应用中，当在工程需求中强调高分子复合材料的韧性和抗断裂时，可通过技术手段适当增加CNTs表面的缺陷数量，尤其是TSW缺陷类型的数量。但当要求确保高分子复合材料的强度时，可尽量减少CNTs表面上缺陷的发生。

6 结论

1) 当CNTs表面出现相同数量的TSW和SV缺陷时，相较于无缺陷CNTs/PPMMA基体，TSW-CNTs/PMMA和SV-CNTs/PMMA复合基体的弹性模量均呈现一定程度降低，其中SV-CNTs/PMMA复合基体的弹性模量最小。

2) TSW-CNTs/PMMA和SV-CNTs/PMMA复合基体的弹性模量均随着CNTs表面缺陷数量增加而逐渐降低，相比CNTs与PMMA之间的界面作用，CNTs自身的弹性模量在影响复合材料的弹性模量中起到主导作用。

3) 对于TSW和SV缺陷，CNTs自身的弹性模量均随着缺陷数量增加而呈现降低趋势，同时由于SV缺陷中存在不连续结构，更易出现应力集中现象，SV-CNTs的弹性模量比TSW-CNTs的弹性模量低。

4) 在实际应用中，若工程需强调高分子复合材料的韧性和抗断裂时，可适当增加CNTs表面的缺陷数量，但当要求确保高分子复合材料的强度时，需要尽量减少CNTs表面缺陷。

参考文献：

[1] KUMAR S K, BENICEWICZ B C, VAIA R A, et al. 50th anniversary perspective: are polymer nanocomposites practical for applications[J]. Macromolecules, 2017, 50(3): 714-731.

[2] 柴丽雅, 李卉, 张国, 等. 不同pH合成的MWCNTs-WO₃复合材料的室温气敏性能[J]. 中南大学学报(自然科学版), 2014, 45(2): 377-382.

CHAI Liya, LI Hui, ZHANG Guo, et al. Synthesis of multi-walled carbon nanotubes and tungsten oxide composites with different pH and gas sensitivity at room temperature[J]. Journal of Central South University(Science and Technology), 2014, 45(2): 377-382.

[3] HUTCHINGS I M. Tribology: friction and wear of engineering materials[J]. Materials & Design, 1992, 13(3): 187.

[4] DEPLANCKE T, LAME O, BARRAU S, et al. Impact of carbon nanotube prelocalization on the ultra-low electrical percolation threshold and on the mechanical behavior of sintered UHMWPE-based nanocomposites[J]. Polymer, 2017, 111: 204-213.

[5] TARFAOUI M, LAFDI K, EL MOUMEN A . Mechanical properties of carbon nanotubes based polymer composites[J]. Composites Part B: Engineering, 2016, 103: 113-121.

[6] ZALAMEA L, KIM H, PIPES R B. Stress transfer in multi-walled carbon nanotubes[J]. Composites Science and Technology, 2007, 67(15/16): 3425-3433.

[7] GAO Xinlin, LI Ke. A shear-lag model for carbon nanotube-reinforced polymer composites[J]. International Journal of Solids and Structures, 2005, 42(5/6): 1649-1667.

[8] SPANOS K N, GEORGANTZINOS S K, ANIFANTIS N K. Investigation of stress transfer in carbon nanotube reinforced composites using a multi-scale finite element approach[J]. Composites Part B: Engineering, 2014, 63: 85-93.

[9] UNWIN P R, GUELL A G, ZHANG Guohui. Nanoscale electrochemistry of sp2 carbon materials: from graphite and graphene to carbon nanotubes[J]. Accounts of Chemical Research, 2016, 49(9): 2041-2048.

[10] LU Qiang, BHATTACHARYA B. Effect of randomly occurring Stone-Wales defects on mechanical properties of carbon nanotubes using atomistic simulation[J]. Nanotechnology, 2005, 16(4): 555-566.

[11] YANG Seunghwa, YU Suyoung, CHO Maenghyo . Influence of Thrower-Stone-Wales defects on the interfacial properties of carbon nanotube/polypropylene composites by a molecular dynamics approach[J]. Carbon, 2013, 55: 133-143.

[12] ZAMINPAYMA E, RAZAVI M E, NAYEBI P. Electronic properties of graphene with single vacancy and Stone-Wales defects[J]. Applied Surface Science, 2017, 414: 101-106.

[13] LI Yunlong, WANG Shijie, WANG Quan, et al. A comparison study on mechanical properties of polymer composites reinforced by carbon nanotubes and graphene sheet[J]. Composites Part B: Engineering, 2018, 133: 35-41.

[14] SCHLEGEL H B. Geometry optimization[J]. Wiley Interdisciplinary Reviews: Computational Molecular Science, 2011, 1(5): 790-809.

[15] RIGBY D, SUN Huai, EICHINGER B E. Computer simulations of poly(ethylene oxide): force field, pvt diagram and cyclization behaviour[J]. Polymer International, 1997, 44(3): 311-330.

[16] LI Yunlong, WANG Shijie, WANG Quan. Enhancement of tribological properties of polymer composites reinforced by functionalized graphene[J]. Composites Part B: Engineering, 2017, 120: 83-91.

[17] LI Yunlong, WANG Shijie, WANG Quan. A molecular dynamics simulation study on enhancement of mechanical and tribological properties of polymer composites by introduction of graphene[J]. Carbon, 2017, 111: 538-545.

[18] LI Yunlong, WANG Quan, WANG Shijie. A review on enhancement of mechanical and tribological properties of polymer composites reinforced by carbon nanotubes and graphene sheet: molecular dynamics simulations[J]. Composites Part B: Engineering, 2019, 160: 348-361.

[19] WELLS B A, CHAFFEE A L. Ewald summation for molecular simulations[J]. Journal of Chemical Theory and Computation, 2015, 11(8): 3684-3695.

[20] ANDERSEN H C. molecular dynamics simulations at constant pressure and/or temperature[J]. The Journal of Chemical Physics, 1980, 72(4): 2384-2393.

[21] BERENDSEN H J C, POSTMA J P M, VAN G W F, et al. Molecular dynamics with coupling to an external bath[J]. The Journal of Chemical Physics, 1984, 81(8): 3684-3690.

[22] RIGBY D, SUN Huai, EICHINGER B E. Computer simulations of poly(ethylene oxide): force field, PVT diagram and cyclization behaviour[J]. Polymer International, 1997, 44(3): 311-330.

[23] LUO Chuanfu, SOMMER J U. Coding coarse grained polymer model for LAMMPS and its application to polymer crystallization[J]. Computer Physics Communications, 2009, 180(8): 1382-1391.

[24] ARASH B, WANG Q, VARADAN V K. Mechanical properties of carbon nanotube/polymer composites[J]. Scientific Reports, 2015, 4: 6479.

（编辑 秦明阳）

收稿日期： 2019 -09 -02; 修回日期： 2019 -11 -21

基金项目(Foundation item)：国家自然科学基金资助项目(51903148, 51905353)；广东省基础与应用基础研究基金资助项目(2020A1515011398)；汕头大学科研启动基金资助项目(NTF19008, NTF19018) (Projects(51903148, 51905353) supported by the National Natural Science Foundation of China; Project(2020A1515011398) supported by the Guangdong Basic and Applied Basic Research Foundation; Projects(NTF19008, NTF19018) supported by the Start-Up Fund of Scientific Research of Shantou University)

通信作者：刘冬，博士，讲师，从事复合材料等研究；E-mail：liud@stu.edu.cn