DOI: 10.11817/j.issn.1672-7207.2019.03.028

广义一维势中热声制冷微循环的性能分析

鄂青^{1, 2}，吴锋^{2, 3}

(1. 华中科技大学 能源与动力工程学院，湖北 武汉，430074；

2. 武汉工程大学 理学院，湖北 武汉，430205；

3. 海军工程大学 动力工程学院，湖北 武汉，430032)

摘要：从工质粒子在不同声波势场条件下的量子力学行为入手，建立一套适用于各种一维势场条件的广义量子热声制冷微循环分析模型并推导出广义量子热声制冷微循环的性能参数表达式。以几个典型的一维势场为例，计算分析工质粒子在不同势场中运动时的循环性能。通过比较，确定当工质粒子工作于一维无限深势阱或谐振势阱条件下时，循环的性能系数和制冷率的综合性能比其他势场条件时的优。研究结果表明：要使热声制冷机性能达到最优，必须对声场进行控制，使其能够在回热器中建立起一维无限深势阱或谐振势阱。

关键词：有限时间热力学；广义一维势；量子热声制冷机微循环；量子热力学

中图分类号：TB65        文献标志码：A         文章编号：1672-7207(2019)03-0726-08

Performance analysis for quantum thermoacoustic refrigeration micro-cycle working in generalized 1D potential

E Qing^{1, 2}, WU Feng^{2, 3}

(1. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;

2. School of Science, Wuhan Institute of Technology, Wuhan 430205, China;

3. Institute of Thermal Science and Power Engineering, Naval University of Engineering, Wuhan 430032, China)

Abstract: A set of analysis model for generalized quantum thermoacoustic refrigeration micro-cycle working in various 1D potential wells was established started with the quantum mechanical behavior of working medium particles under different acoustic potential field conditions. And the performance parameter expressions of the generalized quantum thermoacoustic refrigeration micro-cycle were derived. Taking several typical 1D potentials as examples, the cyclic properties of working medium particles moving in different potential fields were calculated and analyzed. By comparison, it was show that when particle works in 1D infinite deep potential well or resonance potential well, the comprehensive performance of micro-cycle was better than that of other potential well conditions. The results show that, to achieve the optimal performance of the thermoacoustic refrigerator, the sound field must be controlled so that it can establish a 1D infinite deep potential well or resonant potential well in the regenerator.

Key words: finite time thermodynamics; generalized potential well; quantum thermoacoustic refrigeration cycle; quantum thermodynamics

有限时间热力学(finite time thermodynamics，FTT)^[1-5]作为经典热力学的延伸，主要研究非平衡系统中能量流和熵流的规律。在低温系统和微纳米能量转换装置的进一步研究和工程实践中^[6-7]，系统的量子特性变得越来越重要。在有限时间热力学与量子热力学的基础之上，人们建立并分析了不同种类的量子能量转换系统，这代表了热力学的一个重要的发展方向。许多学者在研究量子卡诺^[8]、奥托^[9]、斯特林^[10-11]、迪塞尔^[12]和埃里克森循环时，将其工质视为一系列粒子的集合，这些粒子可以是限制于1个一维无限深势阱的，也可以是限制于谐振势或四次势的，甚至可以是箱势中的极端相对论粒子^[8-15]。WANG等^[16-17]验证了循环性能计算中粒子的能量谱可简化为的结论，并据此给出了广义量子奥托循环的效率及作功量的表达式，在此基础之上，本文作者进一步对由2个等压过程和2个等熵过程组成的热声制冷微循环展开分析。

1  广义量子热声制冷微循环模型的建立

1.1  系统的量子力学基础

普朗克的量子理论给出了粒子的能量表达式为。根据文献[16]，我们可将处于1个广义一维势场内的粒子所具有的能量谱公式简化为

                 (1)

式中：，为粒子的能量；为约化普朗克数；为为了满足量子化的能量表达形式而构建出的频率；为由势阱种类决定的指数；n为量子数；L为势阱宽度；为特定势场所固有的常数；为由势阱种类决定的指数。，和在不同势阱条件下的取值见表1。表1中，c和m分别为粒子的速度与质量；L₁表示系统处于所示循环的宏观状态1时粒子所处势阱的宽度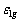；表示系统处于宏观状态1时其中处于基态(n=1)的粒子的能量。这里选用了4种特殊势：一维无限深势阱、谐振势、包含相对论粒子的箱势以及四次势，它们代表了广义一维势的典型情况。系统在宏观状态i的内能的计算式为

                (2)

式中：为处于状态i时n级本征态的粒子的能量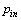；为状态i时处于n级本征态的粒子的概率。p_in应满足如下归一化条件：

                  (3)

在经典热声热力过程中，外界通过振动膜片的运动对系统作功。与振动膜片的经典运动类似，可以假设广义一维势阱的壁面在有限的速度下运动。这样，当系统消耗外界功量或对外界输出功量时，其施加于势阱壁面的合力F_i就可以写为

         (4)

式中：F_in为处于状态i时n级本征态的粒子施加于势阱壁面的力；L_i为处于状态i时的势阱宽度。

将式(1)代入式(4)可得

         (5)

表1  不同势阱的比较

Table 1  Comparison of different potential

1.2  理想广义量子热声制冷微循环

图1所示为理想情况下，热声回热器间气体微团与固体工质的热作用微循环过程。其中，制冷机板叠两端存在明显的温度梯度，板间距小于或等于气体工质热渗透深度的2倍^[18]。设T_x为气团在平衡位置处的平均温度，下标x表示微团的当地坐标；T_m为温度幅值；p₀为系统静压；p_m为压力波动幅值；ξ_m为振荡的位移幅值；为回热器固体壁的纵向温度梯度；为气团处于i(i=1, 3)时的温度与平均温度偏差的绝对值。当气体微团处于最右端状态2时，气团的温度为T_x+T_m，与之相接触的器壁温度为。气团由于振荡快速从右端向左端运动时，由于热弛豫，它没有时间与器壁进行热交换，因而可近似认为该过程是绝热的。当气团到达左端时，温度变为，压力从右端的p₀+p_m变为p₀-p_m，与气团相接触的当地壁温为；当气团到达左端时，由于当地壁温比气团温度高，因而有热量Q₂流向气团，使其温度升高为T_x-T_m，并因膨胀而对邻近气团作功，这一过程可近似为定压吸热过程。图1(b)中的过程4—1为近似的绝热压缩过程，当气团因振荡而从左端向右端快速运动时，由于热弛豫，它没时间与器壁交换热量。当到达右端时，气团的温度变为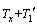，压力变为p₀+p_m。图1中的过程1—2为近似的等压放热过程。当气团从左端振荡到达右端时，气团的温度高于当地壁温，故热量Q₁从气团流向器壁，气团的温度下降为T₁+T_m，此时，气团的状态回复到初始状态，完成1个热力学循环。由热力学第一定律可知，在循环的每个过程中，气体微团作为闭口系统应满足能量守恒方程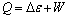(其中，Q和W分别为在任意过程中热力系与外界交换的热量与功，为系统内能)。当系统自外界吸热时Q＞0，向外界放热时，Q＜0；当系统消耗外功时，W＞0，对外界作功时，W＜0。

图1  理想热声制冷微循环示意图

Fig. 1  Diagram of ideal thermoacoustic refrigeration micro-cycle

本文从量子力学的角度分析，可将上述气体微团视为1种被限制在广义一维势阱中的粒子。为了简单起见，在分析量子热声制冷微循环的过程中，只考虑由出现概率较高的2个特征态粒子构成的二能级系统。1台真正的制冷机中的工作介质是由无数这样的粒子组成的。从粒子的量子行为角度分析，每个微循环都可归纳为由2个量子绝热过程和2个量子等压过程环绕而成的。由此得到本文的主要研究对象：理想的广义量子热声制冷微循环(generalized quantum thermoacoustic refrigeration cycle, GQTARC)，如图2所示。

在过程1—2中，系统与1个功源及1个高温热源(温度为T_H)相偶联。随着势阱壁的内移，系统在等作用力的条件下被压缩，此时，它会向高温热源释放大量热量，同时消耗来自于功源的体积功。通常势阱壁的运动耗时相比于高温热源的量子弛豫时间()而言是很多的。也就是说，系统能够保持与高温热源的充分热接触，以确保其始终处于热平衡状态。在系统中，处于激发态(n=2)的粒子的概率p_ie与处于基态(n=1)的粒子的占有概率p_ig=1-p_ie之间应满足玻尔兹曼分布规律：

            (6)

式中：k为玻尔兹曼常数；T_i为系统平衡温度。

图2  理想广义量子热声制冷微循环示意图

Fig. 2  Diagram of ideal generalized quantum thermoacoustic refrigeration micro-cycle

由式(6)可求得系统处于激发态的概率为

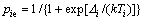          (7)

式中：，为系统处于宏观状态i时各个微观能级间的能量间隔。

由式(7)可得

         (8)

联立式(1)，(3)和(5)可得出在此过程中系统耗功W₁₂的计算式为

＞0 (9)

由于系统始终处于热平衡状态，所以向高温热源放热过程中的换热量Q₁₂为

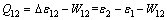        (10)

式中：(i=1, 2)为图2所示状态1和状态2的系统内能。由式(1)~(3)可得

 (11)

将式(9)和式(11)代入式(10)可得

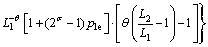＜0   (12)

在过程2—3中，系统与外界没有热交换，外界对系统作的功将全部转换为系统自身内能。在量子绝热过程中，系统内部粒子不会发生能级跃迁，即各能级粒子的概率维持不变，有。由式(1)~(3)和式(5)可得交换的功W₂₃为

＜0     (13)

在过程3—4中，系统在等作用力状态下从1个低温热源(温度为T_L)吸取热量，随着自身体积的膨胀向外界输出功。采用类似于过程1—2的分析方法可得到此过程中交换的功W₃₄和热量Q₃₄分别为：

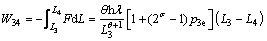＜0  (14)

＞0   (15)

在过程4—1中，由系统绝热压缩有，故消耗的功W₄₁为

＞0      (16)

根据热力学第一定律，在理想广义量子热声制冷微循环过程中，系统的制冷量Q_c为

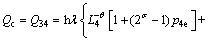
＞0    (17)

系统的净耗功W_net为

＞0    (18)

1.3  循环周期

为了计算完整的循环周期，可假设势阱宽度变化的平均速度为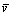。这里，平均变化速度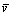应该非常小以使其变化时间远大于系统及热源的弛豫时间()，从而使系统能够始终处于热平衡状态下。则系统经历循环过程1—2—3—4—1所需的时间，即循环周期为^[19]

              (19)

1.4  循环性能参数

由式(1)~(3)可得1个二能级系统的内能为

          (20)

由式(5)可知：1个二能级系统施加在势阱壁上的力可写为

           (21)

由和，可得

           (22)

          (23)

由式(7)可知：当系统处在宏观状态2和状态4时，其内部激发态粒子的概率分别为：

 (24)

           (25)

式中：＞1，为势阱宽度比；T₂和T₄分别为状态点2和状态点4的系统温度。

在理想情况下，可取状态点4和状态点2的温度分别为冷、热端温度(图2)，即

，

显然，p_2e=p_3e是由L₂，T_x，T_m及决定的。对于p_2e，以及已给定的情况，仅由y决定，因此，y是1个重要的控制参数。

将式(22)和式(23)代入式(17)和式(18)可将循环制冷量及耗功量计算式改写为：

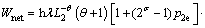
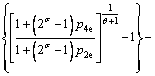
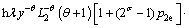
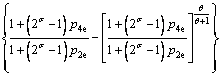
可得出广义量子热声制冷微循环的性能系数C_p为

     (26)

循环的制冷率R为

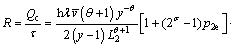
    (27)

令，可得量纲一的制冷率为

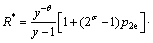
   (28)

对于任意特定的势场，和都是常数。当冷热端温度T₂和T₄已知时，由式(25)可知，式(26)和式(28)所描述的制冷性能系数和制冷率都仅仅是p_2e和势阱宽度比y的函数。

2  广义量子热声制冷微循环性能分析

式(26)和式(28)指出了广义量子热声制冷微循环的性能与系统参数间的关系，在给定了一部分参数的情况下，可用图线的形式对其性能与重要参数间的关系进行研究。

对于工作介质气体微团被束缚于各种一维势阱(如一维无限深势阱、包含相对论粒子的一维势阱、谐振势阱、四次势等)中的量子热声制冷微循环，可统称为一维量子热声制冷微循环(1D quantum thermo-acoustic refrigeration cycle, 1DQTARC)，即一维量子热声制冷微循环包括工作于一维无限深势阱的量子热声制冷微循环(1D infinite potential quantum thermo-acoustic refrigeration cycle, 1DIQTARC)、相对论粒子系统量子热声制冷微循环(relativistic particles quantum thermo-acoustic refrigeration cycle, RQTARC)、谐振系统量子热声制冷微循环(harmonic potential quantum thermo-acoustic refrigeration cycle, HQTARC)和四次势系统量子热声制冷微循环(quartic potential quantum thermo-acoustic refrigeration cycle, QQTARC)。

由表1可见：一维无限深势阱系统与谐振系统具有相同的和，但与基态能量本征值是有差别的。因此，由式(7)可知，当L₂和T₂给定时，这2种系统唯一的区别在于具有不同的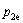；并可推得，其中()为宏观状态2时一维无限深势阱系统(谐振系统)中激发态粒子的概率。换言之，当一维无限深势阱系统和谐振系统的p_2e相同时，由式(26)和式(28)可知，这2类量子热声制冷微循环的性能也会相同。因此，下面的分析中合并考虑这2种情况。为了便于进行比较，在对各种不同势场系统进行分析时，都会采用以下条件：T_x=280 K，T_m/T_x=0.1。

由式(26)可绘出图3所示的粒子在特定量子力学势场中运动时的热声制冷微循环性能系数C_p与p_2e及y之间的关系曲面。当p_2e给定时，C_p会随y的增大呈单调递减的变化。而当y取值较小时，可看出3种不同系统的C_p都会随p_2e的取值变化而出现较明显的变化；但当y不断增大时，p_2e对C_p的影响会变得非常微弱。y在任意取值下，由可求出C_pmax和C_pmin，此时对应的p_2e分别为和。由图3可见：在相同参数条件下，相对论粒子系统中的C_pmax和C_pmin明显比谐振系统的高；而谐振系统中的C_pmax和C_pmin略高于四次势系统的对应值。

由式(28)可绘出图4所示的粒子在特定势场中运动时的热声制冷微循环量纲一的制冷率R^*与p_2e及y之间的关系曲面。由图4可见：当p_2e一定时，R^*与y呈类抛物线关系；而当y一定时，R^*与p_2e亦呈类抛物线关系；并且R^*-y曲线及R^*-p_2e曲线对于3种势场条件都具有相似的形状；此外，存在量纲一的制冷率的最大值以及相应的参数值和(可根据2个极值条件方程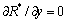，联立得出)。在相同参数条件下，谐振系统的制冷率远高于四次势系统的制冷率；而四次势系统的制冷率又略高于相对论粒子系统的制冷率。此外，制冷机制冷率R^*应不小于0，p_2e的取值应满足条件：。

图5所示为p_2e取不同数值时R^*与C_p之间的关系。由图5可知：在3种情况下，同一C_p所对应的R^*会先随p_2e的增加而增大，达到极限后继续增大p_2e反而会使R^*下降。在相同参数条件下，3种系统中循环的制冷率最大值满足关系：＞＞ ，其中脚标H，R及Q分别代表谐振系统、相对论粒子系统和四次势系统；且3种系统中对应于的C_p虽然很接近但依然满足＞＞。可见，当粒子工作于谐振势中时，循环制冷系数和制冷率的综合效果优于其他2种势场系统的综合效果。

图3  C_p与p_2e及y的关系

Fig. 3  Relationship among C_p, p_2e and y

图4  R^*与p_2e及y的关系

Fig. 4  Relationship among R^*, p_2e and y

图5  R^*与C_p的关系

Fig. 5  Relationship between R^* and C_p

3  结论

1) 当p_2e给定时，工作于一维无限深势阱的量子热声制冷微循环与工作于谐振势的量子热声制冷微循环的性能是相同的。而当L₂和T₂给定时，这2种系统中的p_2e会因为不同而不同。

2) 当p_2e给定时，3种势场条件下循环的C_p都会随y的增加呈单调递减；而当y给定时，3种势场条件下循环的C_p都会随p_2e的取值变化而分别达到最大值C_pmax和最小值C_pmin。通常，C_pmax出现在p_2e＞0.5的区间中，而C_pmin出现在p_2e＜0.5的区间。在相同参数条件下，处于3种不同势场的量子热声制冷微循环满足C_{p R}＞C_{p H}＞C_{p Q}。

3) R^*-y曲线及R^*-p_2e曲线对于3种势场条件下的制冷微循环都具有类似的抛物线形状。在相同参数条件下，处于3种不同势场的量子热声制冷微循环满足 ＞＞，并且R^*达最大值时对应的p_2e小于0.5。当制冷率R^*达最大时，制冷性能系数C_p反而接近最小值。这正好符合制冷率与性能系数不可能同时达最大这一循环特性。

4) 在相同参数条件下，当粒子工作于一维无限深势阱或谐振势场时，循环的制冷系数C_p和制冷率R^*的综合效果比其他2种势场系统的综合效果好。因此，可通过调节声场，使其能够在热声回热器中建立一维无限深的或谐振的势阱条件，来优化热声热机性能。

参考文献：

[1] 吴锋, 陈林根, 孙丰瑞, 等. 斯特林机的有限时间热力学优化[M]. 北京: 化学工业出版社, 2008: 4-17.

WU Feng, CHEN Lingen, SUN Fengrui, et al. Finite time thermodynamic optimization of Stirling engine[J]. Beijing: Chemical Industry Press, 2008: 4-17.

[2] CHEN Lingen, SUN Fengrui. Advances in finite time thermodynamics: analysis and optimization[M]. New York: Nova Science Publishers, 2004: 53-67.

[3] ANDRESEN B. Current trends in finite-time thermodynamics[J]. Angewandte Chemie International Edition, 2011, 50(12): 2690-2704.

[4] WANG Hao,WU Guoxing. Performance analysis and optimum criteria of a quantum dot engine with two discrete energy levels[J]. Physics Letters A, 2012, 376(33): 2209-2216.

[5] CHEN Lingen, LIU Xiaowei, GE Yanlin, et al. Ecological optimization of irreversible harmonic oscillator Carnot refrigerator [J]. Journal of the Energy Institute,2016,86(2): 85-96.

[6] MA Xiaomeng, LI Min, ZHOU Yueming. Nonsequential double ionization of Xe by mid-infrared laser pulses[J]. Optics and Quantum Electronics, 2017, 49(4): 170.

[7] QIN Meiyan, ZHU Xiaosong. Molecular orbital imaging for partially aligned molecules[J]. Optics and Laser Technology,2017,87: 79-86.

[8] LIU Xiaowei, CHEN Lingen, GE Yanlin, et al. Fundamental optimal relation of a generalized irreversible quantum Carnot heat pump with harmonic oscillators[J]. International Journal of Ambient Energy, 2012, 33(3): 118-129.

[9] WU Feng, YANG Zhichun, CHEN Lingen, et al. Work output and efficiency of a reversible quantum Otto cycle[J]. Thermal Science, 2010,14(4): 879-886.

[10] WU Feng, CHEN Lingen, SUN Fengrui, et al. Finite-time exergoeconomic performance bound for a quantum Stirling engine[J]. International Journal of Engineering Science, 2000, 38(2): 239-247.

[11] 吴锋, 汪拓, 陈林根, 等. 量子斯特林热机的输出功和热效率[J]. 机械工程学报, 2014, 50(4): 150-154.

WU Feng, WANG Tuo, CHEN Lingen, et al. Work output and efficiency of a quantum Stirling heat engine[J]. Journal of Mechanical Engineering, 2014, 50(4): 150-154.

[12] ACIKKALP E, CANER N. Application of exergetic sustainable index to the quantum irreversible diesel refrigerator cycles for 1D box system[J]. The European Physical Journal Plus, 2015, 130: 73-1-8.

[13] WANG Jianhui, HE Jizhou, MAO Zhiyuan. Performance of a quantum heat engine cycle working with harmonic oscillator systems[J]. Science in China, Series G, Physics, Mechanics & Astronomy, 2007, 50(2): 163-176.

[14] WANG Jianhui, XIONG Shuangquan, HE Jizhou, et al. Performance analysis of a quantum heat engine working with a particle in a one-dimensional harmonic trap[J]. Acta Physic Sinica, 2012, 61(8): 080509.

[15] E QING, WU Feng, YIN Yong, et al. Optimal power and efficiency of quantum thermoacoustic micro-cycle working in 1D harmonic trap[J]. Journal of Low Temperature Physics, 2017,189(1/2): 84-97.

[16] WANG Jianhui, WU Zhaoqi, HE Jizhou. Quantum Otto engine of a two-level atom with single-mode fields[J]. Physical Review E, 2012, 85(4): 041148.

[17] WANG Jianhui, MA Yongli, HE Jizhou. Quantum Otto engine of a two-level atom with single-mode fields [J]. Euro Physics Letters, 2015, 111(20): 20006.

[18] 阚绪献, 吴锋, 张晓青, 等. 热声热机微热力学循环的最优性能[J]. 武汉理工大学学报, 2009(14): 130-133.

KAN Xuxian, WU Feng, ZHANG Xiaoqing, et al. Performance optimization of a thermoacoustic engine micro-cycle[J]. Journal of Wuhan University of Technology, 2009(14): 130-133.

[19] ANDRESEN B, BERRY R S, ONDRECHEN M J, et al. Thermodynamics for processes in finite time[J]. Accounts of Chemical Research, 1984, 17(8): 266-271.

(编辑  刘锦伟)

收稿日期：2018-03-01；修回日期：2018-05-20

基金项目(Foundation item)：湖北省教育厅科学研究基金资助项目(Q20141506)；武汉工程大学教学研究基金资助项目(X2016036) (Project (Q20141506) supported by the Science Research of Hubei Provincial Department of Education; Project(X2016036) supported by the Teaching Research Funding of Wuhan Institute of Technology)

通信作者：吴锋，博士，教授，从事有限时间热力学及热声热机系统研究；E-mail: wufeng@wit.edu.cn