Pilot studies on two dimensional wave propagation in rock masses

LEI Wei-dong(雷卫东)¹, M.H.Ashraf¹, ZHAO Jian(赵 坚)^{1, 2}

(1. School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798;

2. College of Architecture and Civil Engineering, China University of Mining and Technology, Xuzhou 221008, China)

Abstract: Pilot studies on two dimensional(2-D) wave propagation through single joint or multiple parallel joints were comprehensively conducted, using a suitable data processing method. The possible factors influencing the transmission ratio in 2-D wave propagation under certain circumstances in rock masses were studied. It is found that in the process of 2-D wave propagation, for any radial line, the amount, the stiffness and the spacing of the joints influence the transmission ratio; by contrast, the transmission ratio at any point is independent of the radial distance from the center of wave source. It is also found that the transmission ratio for every grid-point along a single circle can present the transmission ratio for every grid-point after a certain quantity of joints. For the special radian direction(normal to the joints), it is concluded that the transmission ratio is dominated by the normal stiffness; while the influence of shear stiffness is negligible. The radius of the tunnel or borehole for the source wave does not affect the transmission ratio in 2-D wave propagation.

Key words: 2-D wave; transmission ratio; stiffness of joint; wave propagation; pilot study CLC number: TD315

Document code: A

1 INTRODUCTION

In wave propagation, the method of characteristics has been widely used for solving the problems of one dimensional(1-D) wave propagation in continuous elastic materials^[1]. For normally incident 1-D wave propagation across a single or multiple parallel joint(s), combining the theory of displacement discontinuity and method of characteristics, the solutions in terms of magnitudes of the reflection ratio(R) and the transmission ratio(T) were obtained by several researchers^[2-8] for P-wave and S-wave respectively. It was found that the transmission ratio T₁ for single joint is controlled by normalized stiffness of the joint(k/ωz), where k stands for stiffness of the joint; ω stands for angular frequency of the wave; z equivalent to ρc stands for wave impedance, here ρ is the density of rock material and c is the wave speed. It was also found that the transmission ratio T_n is determined by the normalized stiffness(k/ωz), quantity and spacing of the joints for the case of multiple parallel joints.

For practical dynamic problem in rock masses involving wave propagation from an underground explosion source, it becomes 2-D^[9-15]. The stability of the underground structure depends heavily on peak particle velocity(PPV) or peak particle acceleration(PPA), in the sense of combined waves. Investigation on the effects of fractures on wave attenuation is a fundamental topic with theoretical and practical significance^{[5, 6, 8]}.

However, the method of characteristics can not be used in 2-D problems. The theoretical analysis for combined velocity in 2-D wave propagation in rock masses has not been reported in the current literatures.

Besides the factors affecting the transmission T_n in 1-D wave propagation, for 2-D wave propagation in rock masses, stiffness of the joint, in terms of both normal and shear stiffness(j_n and j_s), affects the transmission ratio T_n for combined wave. The position of the grid-point also affects the transmission ratio T_n in 2-D problems. The radius of the tunnel or borehole where the wave originates should be studied as well^[16]. In this paper the authors aim to conduct extensive pilot studies in Universal Distinct Element Code(UDEC) on 2-D wave propagation in rock masses, in terms of the combined velocity wave, hence to determine the affecting factors on the transmission ratio T_n in 2-D wave propagation.

2 FUNDAMETAL BACKGROUNDS

2.1 UDEC model

The geometry of UDEC model is shown in Fig.1, where the width is 100m and the height is 70m. Because the amplitude of velocity for every grid-point is recorded, and a reasonably small mesh size is used in this research to ensure acceptable numerical errors, a very big dimension of the model can not be used due to the current capacity of memory and hard disc of computer. In order to study the wave propagation for the points far away from the center of the explosion source, the center of the cavity is not poisoned at the center of the model. The center of tunnel for dynamic input is positioned at (-40, 0). The first joint in the joint set to be studied is perpendicular to y-axis crossing through (-25, 0), with a normal distance from the center of the cavity of 15m. All the four boundaries are defined as viscous boundaries for dynamic problems. Table 1 lists the properties of the rock material, from a kind of a practical granite^[17].

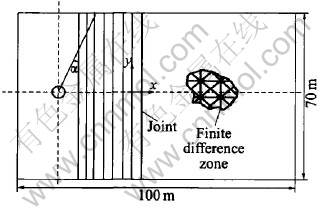
Fig.1  Sketch of UDEC model

Table 1 Mechanical properties and wave propagation velocity in rock material

2.2 Data processing method in UDEC

UDEC is well suited for problems involving jointed rock systems or assemblages of discrete blocks subjected to quasi-static or dynamic conditions. It has strong computation ability, however the data processing and plotting ability is not so good. In Ref.[18], combining UDEC, MATLAB and EXCEL, a method for analysis of velocity/stress amplitude in dynamic problems in a jointed rock mass was developed. The method is used in this research.

2.3 Definition of transmission ratio T_n

In this research the velocity amplitude for a grid-point from the jointed model is frequently compared with velocity amplitude for the corresponding grid-point from the model without joints. The transmission ratio T_n is defined as

where A_joint is the velocity amplitude for the grid-point from the jointed model after the joint; A_intact is the velocity amplitude for the corresponding grid-point from the model without joints; n is the quantity of joints that the wave penetrates through.

2.4 Data fitting method

In order to study the effects of multiple joints, most of the results from the jointed cases will be compared with the results from the case in which no joint is included. The inherent zoning mechanism in UDEC makes the grid-point positions of the model with a joint different from the corresponding grid-point positions of the model without the joints. In order to get the accurate transmission ratio for every grid-point, the position of a grid-point from a jointed model should be the same with corresponding position from the model without joints. In this research, polynomial fitting method is used to fit the position of the grid-point in the jointed model into the position of the grid-point in the model without joints:

f(x_i)=a_nxⁿ_i+a_n-1x^n-1_i+…+a₁x¹_i+a₀(2)

2.5 Definition of radian angle(α)

The radian angle (α) is defined as the angle between the joint and the connection of the incident point on the joint and the center of the dynamic source, as shown in Fig.1. For the upper part, α is smaller than 90°, while α is larger than 90° for the lower part.

3 PILOT STUDY ON PARAMETERS OF JOINTS

In polar coordinate system, the position for any point is determined by angular and radial coordinates. The transmission ratio T_n in 2-D wave propagation in a rock mass is determined by the following factors: the radian angle, the radial coordinate of the point, normalized stiffness of the joint (including normal and shear directions), quantity and the spacing of the joints. If any of the factors does not affect the transmission ratio in 2-D propagation under some circumstances, the problem will be simplified a lot. In order to investigate the effects of one factor on the transmission ratio, only the factor to be studied is changed; while other factors are kept unchanged.

3.1 Transmission ratio along a line with same radian angle

3.1.1 T₁ along a line with same radian angle

The parametric studies are conducted on the UDEC model as shown in Fig.1(with only single joint in the model).

The input wave is a half sine velocity wave(P-wave) with unity amplitude, and the frequency is 200Hz. The mesh size 0.79m is chosen to keep the numerical error less than 2%. The shear and normal stiffness of the joint to be studied are changed as follows: j_s=j_n=0.03K, 0.07K, 0.1K, 0.2K and 0.4K(unit: GPa/m). (In this paper, j_s and j_n are digitally set as value of K or G by a certain quantity, where K, G are the bulk and shear modulus of the rock material. The units of j_n and j_s are stress per length, different from those of K and G). In order to ensure no damage occurring during wave propagation, the cohesion and tensile strength of the joint are given relatively high values.

The properties of the rock material are listed in Table 1.

The amplitude of the velocity for all the grid-point along a line with the same α is recorded, and the corresponding transmission ratio is calculated by Eqn.(1).

Several lines with different α are chosen. The results show that the transmission ratio at any point on a line with the same α is independent of the radial distance from the center of wave source. The transmission ratio at any point along a line with the same α is related to the stiffness of the joint, and the higher the stiffness value, the bigger the transmission ratio. For example, Fig.2 shows the transmission ratio along lines, with α of 90°(a) and 49°(b).

3.1.2 T_n along a line with same radian angle

In Fig.1, parametric studies on effects of multiple parallel joints along a line with the same α are also conducted with different numbers of multiple parallel joints: 2, 4, 6 and 8. The input wave is a half sine velocity wave(P-wave) with unity amplitude, and the frequency is 200Hz. The mesh size of 0.79m is chosen. The normal and shear stiffness of the joint are set as j_s=j_n=0.3K. The ratio of spacing/wavelength varies as 0.01, 0.02, 0.04, 0.05, 0.07, 0.1, 0.13, 0.15, 0.18, 0.2, 0.3 and 0.4.

The properties of the rock material are listed in Table 1.

Similar to the effects of single joint, for the case of multiple joints, the transmission ratio T_n at any point along a line with the same α is independent of the radial distance from the center of wave source, for any quantity and spacing of the joints. For example, Fig.3 shows the transmission ratio

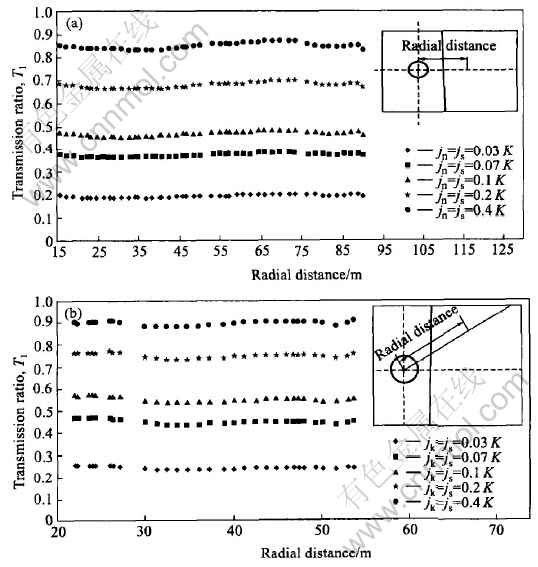
Fig.2  Transmission ratio T₁ along two lines with α of 90°(a) and 49°(b)

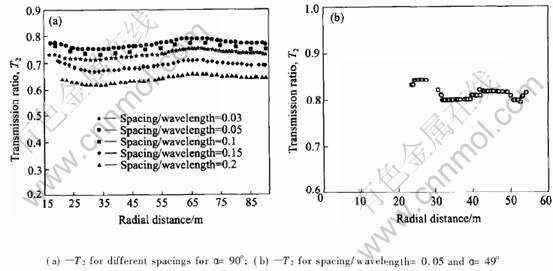
Fig.3 Transmission ratio T₂ for different spacings and α

T₂ along a line, with α of 90°, for 2 joints spaced at 0.03 wavelength, 0.05 wavelength, 0.1 wavelength, 0.15 wavelength and 0.2 wavelength(a), and along the other line with α of 49°(b), for 2 joints spaced at 0.05 wavelength.

3.2 Transmission ratio along a circle

It can be seen that, in the process of 2-D wave propagation through single joint or multiple parallel joints, the transmission ratio at any point along a line with the same α is independent of the radial distance from the wave source center. Based on this important conclusion, it is possible to study the effects of α, along a circle where all the points have the same radial distance from the cavity center, in 2-D wave propagation through a single joint or multiple joints.

For every circle there are two symmetrical lines. The study on effects of a single joint along a circle can be done in one or two quadrants, from 0°to 90° or 180° of radian angle.

3.2.1 T₁ along a circle

The modelling conditions are the same as those in 3.1.1.

In order to study the effects of single joint along a circle, some parametric studies are conducted. For fixed stiffness of the joint(j_n=j_s=0.3K), several circles with different radial distances from the cavity center(R=39m, 50m, 60m, 70m, 80m) are chosen; and for the circle with radial distance from the cavity center of 39m, different stiffness of the joint are chosen(j_n=j_s=0.03K, 0.07K, 0.1K, 0.3K and 0.5K).

The results show that α has effects on 2-D wave propagation through a single joint; while the radial distance does not affect the transmission ratio. For example, Fig.4 shows the transmission ratio T₁ for every grid-point in 2-D wave propagation through a single joint along different circles(with different radial distances from the cavity center of 39m, 50m, 60m, 70m, 80m) for stiffness of joint: j_s=j_n=0.1K.

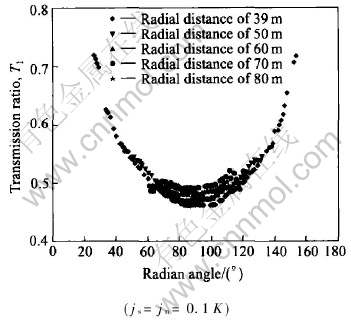
Fig.4  Transmission ratio T₁ along different circles for fixed stiffness

   The results also show that the stiffness values of the joint affect the transmission ratio in 2-D wave propagation along any circle. For example, Fig.5 shows the transmission ratio T₁ for every grid-point along the circle with radial distance from the cavity center of 39m, for cases: j_s=j_n=0.03K, 0.07K, 0.1K, 0.3K and 0.5K.

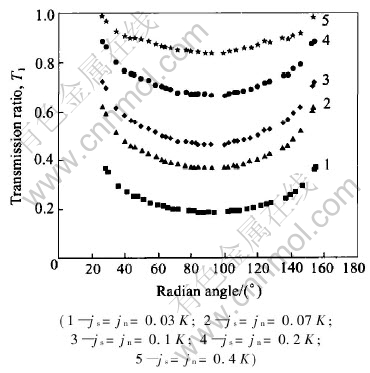
Fig.5  Transmission ratio T₁ along circle with radial distance from cavity center of 39m for different stiffness

3.2.2 T_n along a circle

The modelling conditions are the same as those in 3.1.2.

Similar to the effects of single joint along a circle, a study on effects of multiple joints, along a circle where all the points have the same radial distance from the cavity center, is also performed for any quantity and spacing of the joints. The results show that α has effects on 2-D wave propagation through multiple joints; while the radial distance from the cavity center does not affect the transmission ratio. For example, Fig.6 shows the transmission ratio T₂ along different circles(with radial distances from the cavity center of 39m, 50m, 60m, 70m and 80m) for 2 parallel joints(j_n=j_s=0.3K) spaced at 0.05 wavelength.

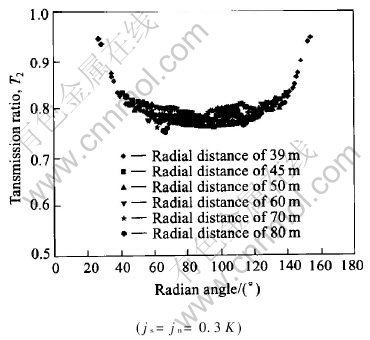
Fig.6  Transmission ratio T₂ along different circles for two joints spaced at 0.05 wavelength for fixed stiffness

3.3 Effects of shear stiffness on T_n along line with radian angle of 90°

In the UDEC model in Fig.1, parametric studies on effects of shear stiffness on the transmission ratio at the grid-point along the line with α of 90° are conducted. The normal stiffness varies as j_n=0.03K, 0.07K, 0.1K, 0.2K, and 0.4K; while the shear stiffness varies as j_s=0.03G, 0.07G, 0.1G, 0.2G, and 0.4G.

The results show that, at the special direction, i.e., normal to the joints (α=90°), the transmission ratio T_n in 2-D wave propagation through single joint or multiple joints is dominated by the normal stiffness of the joint, and the shear stiffness of the joint has negligible influence. For example, Fig.7 shows the transmission ratio T₁ along a circle for different shear stiffness(0.03G, 0.07G, 0.1G, 0.2G and 0.4G) and fixed normal stiffness 0.4K, for 2-D wave propagation through single joint. Fig.8 shows the transmission ratio T₂ along a circle for different shear stiffness(0.03G, 0.07G, 0.1G, 0.2G and 0.4G) and fixed normal stiffness 0.4K, for 2-D wave propagation through 2 joints, spaced at 0.05 wavelength.

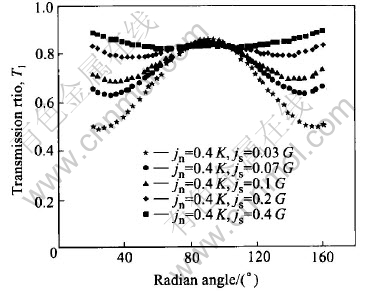
Fig.7  Transmission ratio T₁ for different shear stiffness and fixed normal stiffness

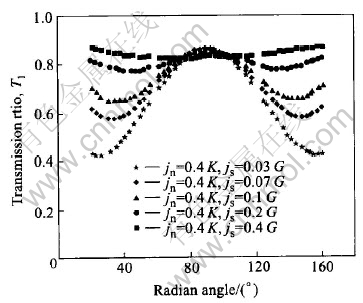
Fig.8  Transmission ratio T₂ for different normalized shear stiffness and fixed normalized normal stiffness along a circle for two joints spaced at 0.05 wavelength

3.4 Discussion and observations

From the results with respects to the effects of the parameters of the joints, there are following observations.

For any radial line, the amount of the joints, the stiffness of joints and the spacing of the joints influence the transmission ratio T_n; along any radian line, the transmission ratio T_n at any point is independent of the radial distance from the center of wave source. The transmission ratio for every grid-point along a single circle can present the transmission ratio for every grid-point with a certain quantity of joints.

At the special direction, i.e., normal to the joint(α=90°), the transmission ratio in 2-D wave propagation through single joint or multiple joints is dominated by the normal stiffness of the joint, and the shear stiffness of the joint has negligible influence.

4 PILOT STUDY ON RADIUS OF CAVITY

Different from the 1-D wave propagation in rock masses, the radius of the tunnel or borehole where the wave originates is involved in 2-D wave propagation. In this part, the effects of the radius of the tunnel or borehole on the transmission ratio T_n along a circle for single joint and multiple parallel joints are studied. In the UDEC model in Fig.1, parametric studies on effects of the radius of the tunnel or borehole along a circle are conducted to investigate the effects of the radius on 2-D wave propagation. Parametric studies on effects of the radius along the special radial line(α=90°) are also conducted.

2m and 5m are chosen for the radius of the tunnel or borehole. The input wave is a half sine velocity wave(P-wave) with unity amplitude, and the frequency is 200Hz. The mesh size of 0.79m is chosen. The normal and shear stiffness of the joint are fixed as j_n=0.4K, j_s=0.4G. The ratio of spacing/wavelength varies as 0.02, 0.035, 0.05, 0.07, 0.13, 0.2, 0.25 and 0.3.

The properties of the rock material are listed in Table 1.

Results show that the radius of the tunnel or borehole for the source pulse wave does not affect the transmission ratio T_n in 2-D wave propagation through both single and multiple parallel joints. For example, Fig.9 shows the comparison of the transmission ratio T₁ along a circle for single joint between two radius values: R=2m and R=5m; Fig.10 shows the comparison of transmission ratio T₂ after two joints spaced at 0.05 wavelength along a circle between two radius values: R=2m and R=5m; Fig.11 shows the transmission ratio T₂ as a function of the ratio of spacing/wavelength for two joints along the special radial line(α=90°).

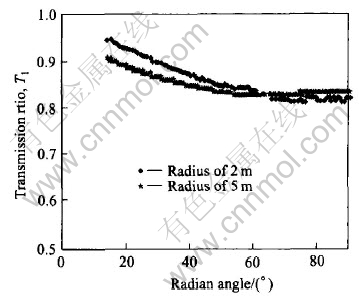
Fig.9  Comparison of transmission ratio T₁ for 2 dimensional wave from tunnels with different radii

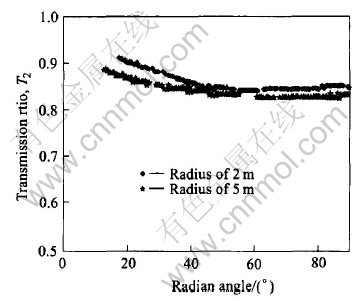
Fig.10  Comparison of transmission ratio T₂ for 2 dimensional wave from tunnels with different radii

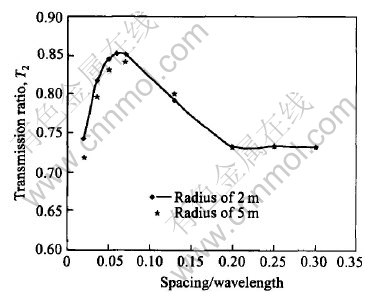
Fig.11  Comparison of transmission ratio T₂ against spacing/wavelength in direction normal to joints for 2 dimensional wave from tunnels with different radii

5 CONCLUSIONS

1) In the process of 2-D wave propagation through multiple parallel joints, for any radial line, the amount of the joints, the stiffness of joints and the spacing of the joints influence the transmission ratio T_n.

2) Along any radial line, the transmission ratio T_n at any point is independent of the radial distance from the center of wave source.

3) The radian angle has effects on 2-D wave propagation through single joint or a set of parallel multiple joints; while the radial distance from the cavity center does not affect the transmission ratio. It implies that the transmission ratio for every grid-point along a single circle can present the transmission ratio for every grid-point with a certain quantity of joints.

4) For the special radial line (α=90°), the transmission ratio is dominated by the normal stiffness; while the influence of shear stiffness is negligible.

5) The radius of the tunnel or borehole for the source pulse wave does not affect the transmission ratio in 2-D wave propagation.

REFERENCES

[1]Bedford A, Drumheller D S. Introduction to Elastic Wave Propagation [M]. Chichester: John Wiley and Sons, 1994.

[2]Schoenberg M. Elastic wave behavior across linear slip interfaces [J]. Journal of Acoustics Society of America, 1980, 68(5): 1516-1521.

[3]Pyrak-Nolte L J. The Seismic Visibility of Fractures [D]. Berkeley, California, USA: University of California, 1988.

[4]Pyrak-Nolte L J, Myer L R, Cook N G W. Anisotropy in seismic velocities and amplitudes from multiple parallel fractures [J]. Journal of Geophysical Research, 1990, 95(B7): 11345-11358.

[5]Cai J G, Zhao J. Effects of multiple parallel fractures on apparent wave attenuation in rock masses [J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 2000, 37(4): 661-682.

[6]Zhao J, Cai J G. Transmission of elastic P-waves across single fractures with a nonlinear normal deformational behavior [J]. Rock Mechanics and Rock Engineering, 2001, 34(1): 3-22.

[7]Pyrak-Nolte L J. The seismic response of fractures and the interrelations among fracture properties [J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1996, 33(8): 787-802.

[8]Zhao X B. Theoretical and Numerical Studies of Wave Attenuation Across Parallel Fractures [D]. Singapore: Nanyang Technological University, 2004.

[9]ZHANG Ji-chun, SONG Lin-ping. Determination of microcrack boundary resulting from rock blasting with seismic traveltime tomography [J]. Trans Nonferrous Met Soc China, 1998, 8(1): 154-160.

[10]XU Guo-yuan, GU De-sheng. Experimental investigation on generation mechanism of explosive stress wave [J]. Trans Nonferrous Met Soc China, 1999, 9(2): 433-439.

[11]Barton N, Chryssanthakis P, Tunbridge L, et al. Predicted and measured performance of the 62 m span Norwegian Olympic Ice Hockey Cavern at Gjovik [J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1994, 31(6): 617-641.

[12]Choi S K, Coulthard M A. Modeling of jointed rock masses using the distinct element method [A]. Rossmanith. Proceedings of Mechanics of Jointed and Faulted rock [C]. Balkema, Rotterdam: 1990. 471-477.

[13]Chen S G, Cai J G, Ihao J, et al. Discrete element modeling of an underground explosion in jointed rock mass [J]. Geotechnical and Geological Engineering, 2000, 18(2): 59-78.

[14]Chen S G, Zhao J. A study of UDEC modeling for blast wave propagation in jointed rock masses [J]. International Journal of Rock Mechanics and Mining Science, 1998, 35(1): 93-99.

[15]Jing L. A review of techniques, advances and outstanding issues in numerical modeling for rock mechanics and rock engineering [J]. International Journal of Rock Mechanics and Mining Science, 2003, 40(3): 283-253.

[16]Graff K F. Wave Motion in Elastic Solids [M]. Ohio, USA: Ohio State University Press, 1979.

[17]Lee C B. Fracturing characteristics of Bukit Timah granite [D]. Singapore: Nanyang Technological University, 2002.

[18]LEI Wei-dong, Ashraf M H, ZHAO J, et al. A new method of processing of wave amplitude using discrete element modeling in rock dynamics [J]. Journal of China University of Mining & Technology, 2005, 34(2): 170-174.

(Edited by YANG Bing)

Foundation item: Project(2002CB412703) supported by the National Basic Research Program of China

Received date: 2004-07-05; Accepted date: 2005-02-17

Correspondence: LEI Wei-dong, PhD Candidate; Tel: +65-98272132; E-mail: p147041779@ntu.edu.sg