基于人字齿轮啮合特性的滑动摩擦功率损失
王成1,高常青1,贾海涛2
(1. 济南大学 机械工程学院,山东 济南,250022;
2. 中国船舶重工集团公司第703研究所,黑龙江 哈尔滨,150036)
摘要:以空间多重共轭啮合理论为基础,利用人字齿轮副轮齿接触特性与承载接触特性,提出一种计算人字齿轮滑动摩擦功率损失的方法。首先,利用人字齿轮副轮齿接触分析(TCA),获得人字齿轮齿面接触路径和印痕。然后,利用人字齿轮副承载接触分析(LTCA),计算得到啮合齿面瞬时椭圆长轴(接触点)上离散点的法向载荷和瞬时接触点的传动误差,把所得到的离散点载荷和传动误差分别转换成齿面瞬时接触点的法向载荷和相对滑动速度,二者与摩擦因数相乘得到人字齿轮瞬时接触点的滑动摩擦功率损失。最后,对人字齿轮齿面所有瞬时接触点的滑动摩擦功率损失进行拟合并积分,最终获得1对人字齿轮轮齿从啮入到啮出的滑动摩擦功损。
关键词:人字齿轮;啮合接触分析;传动效率;滑动摩擦功损
中图分类号:TH132 文献标志码:A 文章编号:1672-7207(2012)06-2173-06
Power losses of sliding friction based on meshing characteristics of double helical gears
WANG Cheng1, GAO Chang-qing1, JIA Hai-tao2
(1. School of Mechanical Engineering, University of Jinan, Jinan 250022, China;
2. No.703 Research Institute of China Shipbuilding Industry Corporation, Harbin 150036, China)
Abstract: A new method was proposed to calculate the sliding friction power losses in double helical gears by considering the geometry and load contact characteristics of double helical gears based on three-dimensional high contact ratio conjugate meshing theory. Firstly, the paths of contact points on tooth surface were obtained from tooth contact analysis (TCA) of double helical gears. Secondly, the normal force of discretized points on the major axis of instantaneous contact ellipse and the loaded transmission errors of instantaneous contact points were calculated from loaded tooth contact analysis (LTCA) of double helical gears. Then, the normal force of discretized points and the loaded transmission errors were transformed into the normal force and relative sliding speed of instantaneous contact points, respectively. Multiplying these two with the friction coefficient causes the sliding friction power losses of instantaneous contact points. Finally, the sliding friction power loss from gear-in to gear-out is obtained by fitting and integrating the power losses of instantaneous contact points.
Key words: double helical gears; meshing contact analysis; transmission efficiency; sliding friction power losses
人字齿轮传动不但具有斜齿轮传动的优点,而且能克服斜齿轮传动时因产生轴向力而不能采用过大螺旋角的缺点[1],在矿山、舰船等大功率机械传动中被普遍使用。齿轮的传动效率关系到其传动质量,造成齿轮传动功率损失的因素包括[2]轮齿间啮合功率损失(主要因素)、轴系零件的摩擦和搅油损失以及风损。其中轮齿间啮合功率损失是由齿面滚动摩擦和滑动摩擦引起,而滑动摩擦又是造成齿轮啮合功率损失的主要原因[3]。查齿轮传动效率表、试验测试和公式计算是3种确定齿轮效率的途径。其中,查表法易产生较大的误差;试验法最准确,但结果不通用,且易受各种因素的干扰,但相比较而言,采用计算的方法更为可行。周哲波[3]通过分析弹流润滑状态下齿面相对滑动速度和齿面载荷,推导出直齿圆柱齿轮和斜齿圆柱齿轮功率损失的计算公式。姚建初等[4]从计算啮合点的啮合效率入手,通过积分的方法,得到一对轮齿从进入啮合到退出啮合的传动效率。但上述方法均未涉及齿轮制造、安装误差和轮齿修形。此外,文献[3]中对所受载荷进行简化处理,即假定同时参加啮合的轮齿所受载荷相同,因此,以上方法均无法进行传动效率的精确计算。国外对于齿轮传动功率损失的研究主要是利用试验的方法[5-6]。Diab等[2]针对功率损失原因建立相应的分析模型,但未研究如何求解。通过轮齿接触分析(TCA)和承载接触分析(LTCA)可精确得到齿轮啮合分析数据[7],为齿轮传动效率的计算提供一种新的思路。基于以上思想,谷建功等[8]提出弧齿锥齿轮啮合的滑动摩擦功损的计算方法,但其在对齿面相对滑动速度的处理上是按空载情况下计算的。王成 等[9]提出斜齿轮滑动摩擦功率损失的计算方法,但在计算时采用简化的方法,所得的数值存在误差。为此,本文作者以空间多重(多啮对)共轭啮合理论为基础,借助人字齿轮副啮合接触分析的结果进行人字齿轮滑动摩擦功率损失的计算。
1 人字齿轮副轮齿接触分析
图1所示为考虑修形和制造安装误差下的人字齿轮副轮齿接触分析模型, 其中Ⅰ和Ⅱ分别为人字齿轮副左右端的斜轮齿副。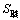 和
和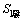 分别为左端主、从动轮轮体上的固定坐标系,
分别为左端主、从动轮轮体上的固定坐标系, 和
和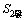 分别为右端主、从动轮轮体上的固定坐标系,与主、从动轮一起运动;φ1Ⅰ和φ1Ⅱ分别为左端主、从动轮的瞬时转角,φ2Ⅰ和 φ2Ⅱ分别为右端主、从动轮的瞬时转角;Sh1和Sh2,Sk1和Sk2是固定坐标系,Sh1和Sh2分别表示主动轮理论初始安装位置,Sk1和Sk2分别表示从动轮理论初始安装位置,互相平行,且相距为E;SfⅠ和SfⅡ为设在箱体上的固定坐标系,分别与左右端主动轮的理论初始位置重合(即分别与Sh1和Sh2重合)。
分别为右端主、从动轮轮体上的固定坐标系,与主、从动轮一起运动;φ1Ⅰ和φ1Ⅱ分别为左端主、从动轮的瞬时转角,φ2Ⅰ和 φ2Ⅱ分别为右端主、从动轮的瞬时转角;Sh1和Sh2,Sk1和Sk2是固定坐标系,Sh1和Sh2分别表示主动轮理论初始安装位置,Sk1和Sk2分别表示从动轮理论初始安装位置,互相平行,且相距为E;SfⅠ和SfⅡ为设在箱体上的固定坐标系,分别与左右端主动轮的理论初始位置重合(即分别与Sh1和Sh2重合)。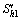 和
和 分别为制造安装误差造成人字齿轮轴向移动后的坐标系。
分别为制造安装误差造成人字齿轮轴向移动后的坐标系。
人字齿轮啮合时,在固定(公共)坐标系下,其两齿面瞬时啮合点处的位置矢量和法线矢量相等,即人字齿轮左右端齿面接触方程分别为(i=Ⅰ,Ⅱ):
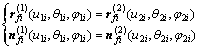 (1)
(1)
人字齿轮边缘接触方程为:
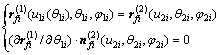 (2)
(2)
φ1Ⅰ和φ1Ⅱ的关系为:
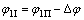 (3)
(3)
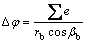 (4)
(4)
其中:uji(j =1,2;i=Ⅰ,Ⅱ)是刀具齿面参数;θji是齿条刀的坐标系变换到齿轮坐标系所转过的角度;Δφ是左右端齿面加工误差造成的转角差;∑e是左右端齿面的加工误差;rb是主动轮的基圆半径;βb是主动轮的基圆螺旋角。
分别取φ1Ⅰ和φ1Ⅱ为输入量,通过求解式(1)和(2),可得到人字齿轮齿面接触路径和印痕。斜齿轮和人字齿轮的TCA见文献[10-11]。
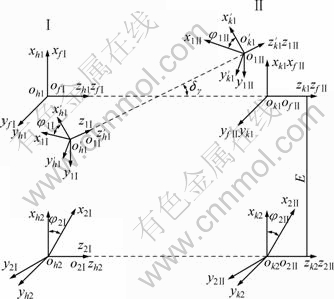
图1 人字齿轮副轮齿接触分析模型
Fig.1 Coordinate system for double helical gears meshing
2 人字齿轮齿面瞬时接触点的法向载荷与相对滑动速度的计算
2.1 人字齿轮副承载接触模型与分析
图2所示为人字齿轮LTCA模型。图中为过齿面瞬时接触椭圆长轴(受载时,瞬时接触点变为椭圆,由于椭圆长轴远大于短轴,因此,只考虑椭圆长轴)的法截面,这里,瞬时接触椭圆长轴被离散成n个点。
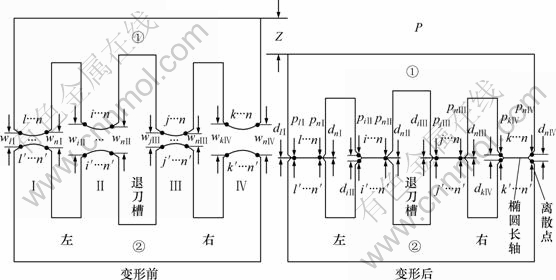
图2 人字齿轮副加载接触分析模型
Fig.2 Loaded contact analysis model of double helical gears
承载接触分析方法及人字齿轮副的承载接触分析的原理是根据变形位移协调方程和左右端轴向力平衡条件,借助有限元法和非线性数学规划法进行求解,得到齿轮在修形和误差下的齿面载荷分布和承载传动误差,见文献[12-13]。通过人字齿轮副承载接触分析,得到啮合周期内所有齿面瞬时接触椭圆长轴上离散点的法向载荷和齿面瞬时接触点的传动误差。
2.2 人字齿轮齿面瞬时接触点与啮合位置的对应 关系
人字齿轮在啮合过程中,存在多对齿同时啮合的情况。这里,假定每对齿的几何与力学性能都是一致的。因此,在计算人字齿轮副轮齿接触分析和承载接触分析时将它们按左右端分别放在一对齿上计算。这样,仅需1个周期LTCA的求解,即能获得1对人字齿轮轮齿从啮入到啮出的全部承载啮合过程。在轮齿接触分析时,左端主动轮的转角φ1Ⅰ满足:
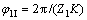 (5)
(5)
其中:K为人字齿轮TCA和LTCA的求解周期内给定的啮合位置数;Z1为主动轮的齿数。φ1Ⅱ与φ1Ⅰ的关系见式(3)。
图3所示为K=5时某人字齿轮副经轮齿接触分析计算得到的1对轮齿从进入啮合到退出啮合的齿面接触路径和印痕。假定在某啮合位置左端齿对在第8点接触,那么,在该啮合时刻,左端共有3对齿同时接触,即前一对齿在第3点接触,后一对齿在第13点接触。而此时右端同时也有3对齿啮合,它们分别在第18,23和28点接触。根据上述分析,得出1个啮合周期内,齿面瞬时接触点所对应的啮合位置,如表1所示。
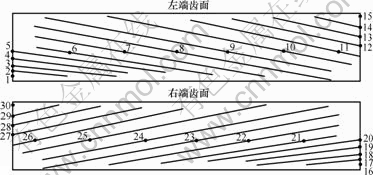
图3 齿面接触路径和印痕
Fig.3 Path of contact on tooth surface
表1 齿面瞬时接触点与啮合位置的对应关系
Table 1 Meshing position corresponding to contact ellipse

2.3 人字齿轮齿面瞬时接触点所受法向载荷的计算
在人字齿轮副轮齿接触分析时,瞬时接触椭圆长轴被离散成n个点(见图2)。利用人字齿轮副承载接触分析,得到这些离散点的法向载荷,第j个瞬时接触点的法向载荷为:
 (6)
(6)
其中:n为人字齿轮齿面瞬时接触点j(椭圆长轴)被离散的点数;Fi(i=1,2,…,n)为瞬时接触点j上相应离散点i所受到的法向载荷。
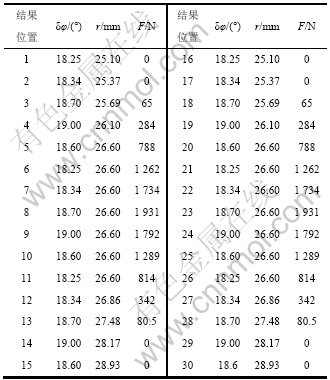
前面假定每对轮齿的几何与力学性能一致,同样,通过1个啮合周期LTCA的求解,可得到1对人字齿轮轮齿从啮入到啮出的全部载荷。例如,当K取5时,对位置3的进行求解,得到位置3,8,13,18,23和28上离散点的法向载荷。依此类推,对齿面瞬时接触位置1、2、4和5进行求解,得到相应瞬时接触点(见表1)上离散点的法向载荷。利用1个啮合周期(这里,K=5次)LTCA的计算,获得人字齿轮齿面全部瞬时接触点上离散点所受的法向载荷。然后,根据式(6),得到齿面瞬时接触点所受的法向载荷。
2.4 人字齿轮齿面瞬时接触点相对滑动速度的计算
类似上节中齿面瞬时接触点法向载荷的求解,利用1个啮合周期LTCA的求解,获得1对人字齿轮轮齿啮入到啮出齿面全部瞬时接触点的传动误差。
传动误差用来表征从动轮转角的实际值与理论值之差,是两齿面瞬时接触点相对滑动速度产生的原因。据此,人字齿轮副齿面瞬时接触点相对滑动速度为:
 (7)
(7)
其中:t为人字齿轮主动轮转过相邻瞬时接触点所需的时间;w1和z1分别为人字齿轮主动轮的角速度和齿数;N为1对人字齿轮轮齿从啮入到啮出齿面瞬时接触位置(点)的个数;δφ和w12分别为人字齿轮动轮(包括主动轮和从动轮)齿面瞬时接触点的传动误差和相对滑动角速度,j=1,2,…,N;rj(j=1,2,…,N)为人字齿轮齿面瞬时接触点到主动轮回转中心的距离;v12为人字齿轮齿面瞬时接触点的相对滑动速度。
3 人字齿轮滑动摩擦功率损失的 计算
在人字齿轮副轮齿接触分析时,齿面瞬时接触点的个数与啮合周期内位置取值有关,理论上齿面瞬时接触点可得到无穷多个。而在实际计算中,不可能取无穷个啮合位置。这里借助MATLAB软件,首先利用式(8)计算得到瞬时接触点的滑动摩擦功损,继而得到小轮转角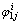 (j=Ⅰ,Ⅱ,i=1,2,…,N,N为1对轮齿从啮入到啮出齿面瞬时接触点的个数)对应的滑动摩擦功损
(j=Ⅰ,Ⅱ,i=1,2,…,N,N为1对轮齿从啮入到啮出齿面瞬时接触点的个数)对应的滑动摩擦功损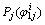 。其次,用MATLAB将这些瞬时接触点(
。其次,用MATLAB将这些瞬时接触点(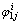 ,
,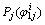 )拟合成曲线方程(见式(9))。
)拟合成曲线方程(见式(9))。
最后,通过对方程求导分别得到左右端轮齿从啮入到啮出的滑动摩擦功率损失(见式(10)),将两者相加,即得到人字齿轮的滑动摩擦功率损失。
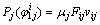 (8)
(8)
 (9)
(9)
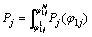 (10)
(10)
4 算例
利用上述方法计算1对人字齿轮的滑动摩擦功率损失(小轮主动,这里未考虑制造和安装误差),该对人字齿轮的参数见表2(为与文献[9]中斜齿轮的滑动摩擦功损进行比较,人字齿轮受载情况和左右两端齿轮副的几何性质与文献[9]中取为相同)。《齿轮手册》建议混合弹流润滑条件下齿轮的平均摩擦因数μ=0.03~0.07,这里取μ=0.05。
图3所示为人字齿轮副轮齿接触分析后的小轮齿面接触路径与印痕。图4和图5所示分别为通过人字齿轮副承载接触分析后小轮齿面瞬时接触点(椭圆长轴)上离散点的载荷分布和传动误差(人字齿轮TCA和LTCA的结果见表3)。根据式(6)和(7),把离散点载荷和传动误差分别转换成齿面瞬时接触点的法向载荷和相对滑动速度。借助MATLAB对接触点功损进行拟合并积分,最终得到1对人字齿轮轮齿从啮入到啮出的滑动摩擦功率损失P= 17.14 W(图6为齿面瞬时接触点滑动功损拟合曲线)。因此,人字齿轮啮合效率为:
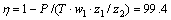 (11)
(11)
表2 人字齿轮的参数
Table 2 Parameters of double helical gears
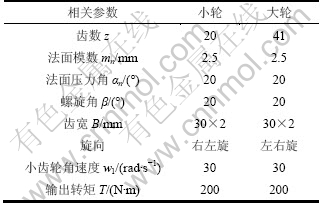
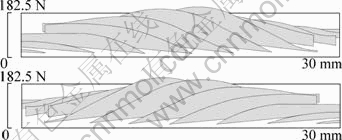
图4 人字齿轮齿面载荷分布
Fig.4 Tooth surface load distribution
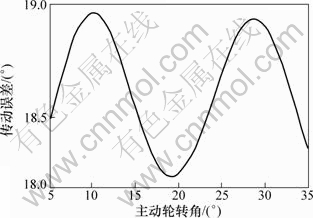
图5 人字齿轮承载传动误差
Fig.5 Loaded transmission errors
表3 人字齿轮TCA和LTCA的计算结果
Table 3 Corresponding calculation results of TCA and LTCA
根据《齿轮手册》,7级及以上精度、润滑良好的单级圆柱齿轮传动效率在0.98以上,而利用本文提出的方法计算得到的人字齿轮啮合效率满足上述范围(不低于下限值,这符合文中除涉及滑动摩擦功损之外而未涉及其他功率损失这一情况);通过与文献[9]中斜齿轮的滑动摩擦功损相比,人字齿轮的滑动摩擦功损要小(斜齿轮啮合效率为0.99),这符合人字齿轮重合度大从而传动平稳的特点。
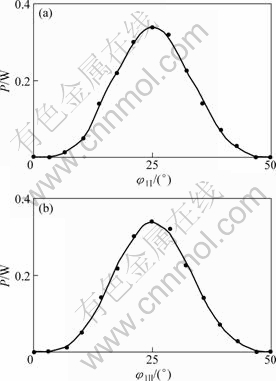
图6 齿面瞬时接触点滑动功率损失拟合曲线
Fig.6 Fitted curve of raw data on power losses
5 结论
(1) 利用人字齿轮副轮齿接触特性与承载接触特性,获得人字齿轮齿面瞬时接触点的法向载荷和相对滑动速度,利用MATLAB拟合出人字齿轮副从进入啮合到退出啮合齿面瞬时接触点的滑动摩擦功率损失与小轮转角之间的函数关系式,然后利用积分求出混合弹流润滑状态下人字齿轮的滑动摩擦功率损失。
(2) 本算法的计算结果满足常见圆柱齿轮传动效率的范围。通过与相同情况下的斜齿轮比较,人字齿轮的滑动摩擦功率损失要比斜齿轮的小,符合人字齿轮传动平稳的特点。
参考文献:
[1] Amendola J B. Single vs double helical gears[J]. Turbomachinery International. 2006, 47(5): 34-38.
[2] Diab Y, Ville F, Velex P. Investigations on power losses in high-speed gears[J]. J Engineering Tribology, 2006, 220(3): 191-198.
[3] 周哲波. 弹流润滑状态下齿轮啮合效率的研究[J]. 机械设计, 2004, 21(12): 40-42.
ZHOU Zhe-bo. Study on gear meshing efficiency under condition of elastohydrodynamic lubrication[J]. Journal of Machine Design, 2004, 21(12): 40-42.
[4] 姚建初, 陈义保, 周济, 等. 齿轮传动啮合效率计算方法的研究[J]. 机械工程学报, 2001, 37(11): 18-21.
YAO Jian-chu, CHEN Yi-bao, ZHOU Ji, et al. Study on a method for calculating gearing meshing efficiency[J]. Chinese Journal of Mechanical Engineering, 2001, 37(11): 18-21.
[5] Aarthy Vaidyanathan, B. Tech. An experimental investigation of helical gear efficiency[D]. Ohio: Ohio State University, 2009: 36-97.
[6] Petry-Johnson T, Kahraman A, Anderson N E, et al. An experimental investigation of spur gear efficiency[J]. Journal of Mechanical Design, 2008, 130(6): 062601.
[7] Litvin F L, Fuentes A. Gear geometry and applied theory, second edition[M]. New York: Cambridge University Press, 2004: 10-20.
[8] 谷建功, 方宗德, 苏进展, 等. 混合弹流润滑下弧齿锥齿轮传动啮合效率计算方法[J]. 农业机械学报, 2010, 41(5): 188-192.
GU Jian-gong, FANG Zong-de, SU Jin-zhan, et al. Calculation of meshing efficiency for spiral bevel gears under the condition of mixed elastohydrodynamic lubrication[J]. Transactions of Chinese Society for Agriculture, 2010, 41(5): 188-192.
[9] 王成, 方宗德, 贾海涛. 斜齿轮滑动摩擦功率损失的计算[J]. 燕山大学学报, 2009, 33(2): 99-102.
WANG Cheng, FANG Zong-de, JIA Hai-tao. The calculation of sliding friction power losses on helical gears[J]. Journal of Yanshan University, 2009, 33(2): 99-102.
[10] Litvin F L, LU Jian, Townsend D O, et al. Computerized simulation of meshing of conventional helical involute gears and modification of geometry[J]. Mechanism and Machine Theory, 1999, 34(1): 123-147.
[11] 王成, 方宗德, 王平. 人字齿轮修形设计与轮齿接触分析[J]. 燕山大学学报, 2009, 33(4): 288-293.
WANG Cheng, FANG Zong-de, WANG Ping. Double helical gears modification design and tooth contact analysis[J]. Journal of Yanshan University, 2009, 33(4): 288-293.
[12] Li S T. Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors, assembly errors and tooth modifications[J]. Mechanism and Machine Theory, 2007, 42(1): 88-114.
[13] 王成, 方宗德, 谷建功, 等. 人字齿轮承载接触分析与试验[J]. 航空动力学报, 2010, 25(3): 718-722.
WANG Cheng, FANG Zong-de, GU Jian-gong, et al. Loaded tooth contact analysis of double helical gears and experimental investigation[J]. Journal of Aerospace Power, 2010, 25(3): 718-722.
(编辑 邓履翔)
收稿日期:2011-06-05;修回日期:2011-11-21
基金项目:国家自然科学基金资助项目(50905074);山东省优秀中青年科学家科研奖励基金资助项目(BS2011ZZ002);济南大学科研基金资助项目(XKY1012);济南大学博士基金资助项目(XDS1022)
通信作者:王成(1977-),男,山东莱州人,博士,讲师,从事机械传动等研究;电话:0531-82765925;E-mail:me_wangc@ujn.edu.cn