循环冲击荷载下热处理对花岗岩能量耗散的影响
来源期刊:中国有色金属学报(英文版)2019年第2期
论文作者:舒荣华 尹土兵 李夕兵 殷志强 唐礼忠
文章页码:385 - 396
关键词:能量耗散;花岗岩;循环冲击;压缩;热处理
Key words:energy dissipation; granite; cyclic impact; compression; thermal treatment
摘 要:深部采矿中高温导致岩石产生热损伤。为了了解循环冲击作用下热处理对岩石能量耗散的影响,运用霍普金森实验系统进行热处理后岩石的循环冲击加载实验,分析能量耗散、能量耗散率、冲击次数、单位体积能耗以及破坏模式与温度之间的关系。实验结果表明:第一次冲击的反射能随着温度的升高逐渐增大并且最终超过吸收能,然而,总反射能在200 °C后随着温度的升高逐渐减小;第一次冲击的吸收能与总吸收能随着温度的升高逐渐减小,能量吸收率也相应减小;与吸收能表现出相似的规律,随着温度的升高,第一次冲击的透射能与总透射能逐渐减小,能量透射率也随之减小,相反地,能量反射率却逐渐增大。随着温度的升高,岩石破坏所需的冲击次数逐渐减少;另外,当岩石经受不同热处理后,其破坏模式也有所不同,即:当温度高时,尽管吸收的能量低,岩石试样在经过几次冲击后破碎成粉状。
Abstract: High temperature treatment causes thermal damage to rocks in deep mining. To study the thermal effect on the energy dissipation of rocks during the dynamic cyclic loading, cyclic impact loading experiments of heat-treated rocks were carried out using the splitting Hopkinson pressure bar (SHPB) experimental system. The correlations among the energy dissipation, energy dissipation rate, impact times, accumulated absorbed energy per volume, failure mode and temperature were analyzed. The results show that the reflected energy under the first impact increases and finally exceeds the absorbed energy when the temperature increases; however, the total reflected energy decreases above 200 °C. The absorbed energy under the first impact and the total absorbed energy all decrease as the temperature increases, the rates of which decrease accordingly. And the same phenomenon appears for the transmitted energy and the rate of the transmitted energy. On the contrary, the rate of the reflected energy increases with the rising temperature. When the temperature increases, the fewer impact times are needed to destroy the sample. In addition, the failure modes are different when the rock is treated at different temperatures; that is, when the temperature is high, even though the absorbed energy is low, the sample breaks into powder after several impacts.
Trans. Nonferrous Met. Soc. China 29(2019) 385-396
Rong-hua SHU1, Tu-bing YIN1, Xi-bing LI1, Zhi-qiang YIN2, Li-zhong TANG1
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. Key Laboratory of Deep Coal Mine Excavation Response and Disaster Prevention and Control, Anhui University of Science and Technology, Huainan 232001, China
Received 7 January 2018; accepted 16 April 2018
Abstract: High temperature treatment causes thermal damage to rocks in deep mining. To study the thermal effect on the energy dissipation of rocks during the dynamic cyclic loading, cyclic impact loading experiments of heat-treated rocks were carried out using the splitting Hopkinson pressure bar (SHPB) experimental system. The correlations among the energy dissipation, energy dissipation rate, impact times, accumulated absorbed energy per volume, failure mode and temperature were analyzed. The results show that the reflected energy under the first impact increases and finally exceeds the absorbed energy when the temperature increases; however, the total reflected energy decreases above 200 °C. The absorbed energy under the first impact and the total absorbed energy all decrease as the temperature increases, the rates of which decrease accordingly. And the same phenomenon appears for the transmitted energy and the rate of the transmitted energy. On the contrary, the rate of the reflected energy increases with the rising temperature. When the temperature increases, the fewer impact times are needed to destroy the sample. In addition, the failure modes are different when the rock is treated at different temperatures; that is, when the temperature is high, even though the absorbed energy is low, the sample breaks into powder after several impacts.
Key words: energy dissipation; granite; cyclic impact; compression; thermal treatment
1 Introduction
With the rapid development of the economy in the country, more and more resources are needed, especially mineral resources, nevertheless mineral resources are gradually being exhausted. Thus, in recent years, it has become necessary to enter into a large-scale development of mineral resources, most of which involves deep underground mining. The deep rock mass, which bears high temperature, high stress and high dynamic disturbance, is very different to the shallow rock mass. Since problems associated with deep rock mechanics became a research hot spot, lots of researchers have devoted themselves to solving these problems [1-3]. Temperature plays an important role in rock engineering, such as the deep mining, the disposal of highly radioactive nuclear waste, the underground storage and mining of petroleum and natural gas, the development and utilization of geothermal resources, and the post-disaster reconstruction of underground rock engineering. However, it is needed to consider the mechanical problems of rock under high temperatures and cyclic impact loadings at the same time, such as frequent drilling and blasting. The energy dissipation of rock under thermal treatment and cyclic impact loading still is blank. Hence, it is worthwhile to study the energy dissipation of heat-treated rock under cyclic impact loading.
Since temperature plays a key role in deep rock practices, many researchers have investigated the effect of thermal treatment on the physical and mechanical properties of various rocks [4-8]. In recent years, LIU and XU [9] investigated the thermal effect on the mechanical behavior of rock and discovered that the dynamic mechanical behavior of rock was greatly related to temperature. And, some studies were devoted to researching on the thermal effects on the dynamic strength of various rocks [10-12]. However, as PAVLOVIC [13] expounded, the maximum stress depends on the material properties, structural geometry and boundary conditions. Hence, the strength failure criterion in terms of the nominal stress is not suitable for a structure made of a brittle material. Instead, the failure process for a brittle material can be described by the elastic energy dissipated in the structure. In addition, HUDSON et al [14] considered that the peak strength of a sample is a function of the boundary conditions of the test, and hence is not an inherent material property. As a result, research on the energy dissipation in the process of impact experiment could be a suitable way to understand the failure mechanism of rock. But few studies were focused on energy dissipation of rock [15-17]. At different temperatures, YIN et al [18] carried out the impact experiments of sandstone samples with different axial pressures. The results showed that temperature was a very important factor which affects the energy dissipation of rocks.
When being subjected to dynamic or cyclic loads, different materials respond in different ways. Some materials become stronger and more ductile, while others become weaker and more brittle [19]. There is much difference between the dynamic and static mechanical properties of rocks. Many researchers studied the dynamic mechanical properties [20-22], but there was less literatures focused on the dynamic cyclic loading. Instead, research on the mechanical properties of rock under static cyclic loads was more common [23-25].
In this work, SHPB tests on granite subjected to high temperature were carried out under dynamic cyclic impact loading. The correlations among energy dissipation, energy dissipation rate, accumulated absorbed energy per volume, impact times, failure mode and temperature were investigated and discussed.
2 Experimental
2.1 Sample preparation
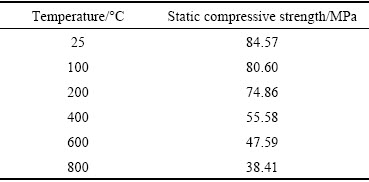
The heat-treated granite samples were prepared for testing. According to the standard requirements of the International Society of Rock Mechanics (ISRM) [26], the samples were made into cylinders with dimensions of d50 mm × 50 mm and d50 mm × 100 mm, respectively, by cutting and polishing, controlling parallelism within ±0.05 mm and the surface flatness within ±0.02 mm. Samples of similar wave velocity were selected, numbered and heated to the designed temperatures. As shown in Fig. 1, the rock sample is mainly composed of quartz, biotite and potassium feldspar. After initial trials in which the static strengths given in Table 1 were taken into consideration, the appropriate incident energy is around 60 J, and the air pressure is about 0.6 MPa.

Fig. 1 Petrographic microscopy image of granite
Table 1 Static compressive strength of heat-treated granite
2.2 Experimental apparatus
The experiment on the heat-treated rock under cyclic impact loading can be achieved through the SHPB experimental system in accordance with the suggested method for dynamic rock testing [27], together with the auxiliary devices, as shown in Fig. 2. The SHPB system mainly includes a spindle punch, an emission cavity, a gas gun, an incident bar (2000 mm in length), a transmission bar of 1500 mm, an absorbing bar of 500 mm in length, a data-processing device and a signal recording device. The suitable d50 mm bar is made of high-strength alloy, with an ultimate strength of 800 MPa, a wave velocity of 5400 m/s and a density of 7810 kg/m3. The spindle punch plays an important role in producing a stable strain rate of half sinusoidal stress wave. The waves (incident wave, reflected wave and transmitted wave) are measured by the signals recorded through strain gauges which are fixed on the incident bar and transmission bar. In addition, the heating furnace (SX-4-10) designed for a rated power of 4 kW and a maximum temperature of 1050 °C, mainly contains a high-temperature furnace and temperature controller. And the static experiment could be carried out by an electro-hydraulic and servo-controlled material testing machine of the type RMT-150. The rock and soil engineering quality detector which is used for wave velocity measurement mainly consists of an ultrasonic emission and receiving transducer. The Vernier caliper and electronic balance are for length, diameter and quality measurement, respectively.
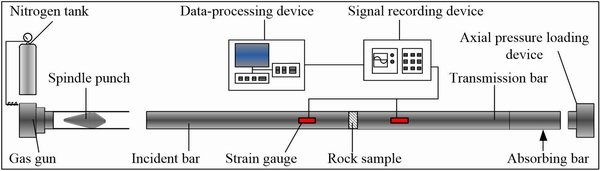
Fig. 2 Splitting Hopkinson pressure bar (SHPB) experimental system
2.3 Experimental method
To guarantee that experiments on heat-treated rock under cyclic impact loading could be carried out successfully, the experimental method was designed as follows. Six groups of samples for thermal treatment at 25, 100, 200, 400, 600 and 800 °C were designed. Each group consisted of no less than five samples for the dynamic experiment and two samples used for the static test. In addition, the basic parameters of the rocks should be measured before the thermal treatment, such as wave velocity, length, diameter and quality. The values were averaged after measuring more than three times. The target temperature with the heating rate of 2 °C/min, once reached, was kept constant for 3 h in order to ensure uniform heating of the samples. Besides, the wave velocity and the quality were measured again after the rock samples were slowly cooled in the heating body. After the thermal treatment, static experiments were carried out at every classified temperature. In addition, because of the existence of a threshold value in the cyclic loading experiment [28], the cyclic loads should ensure that various heat-treated samples could finally be broken after several impacts. In order to find the appropriate loading that could cause the heat-treated (800 °C) sample to fail after undergoing impacts twice, a trial should be carried out to determine the appropriate cyclic loads. Finally, the cyclic impact loading experiments on the heat-treated rocks could be carried out.
3 Energy calculation
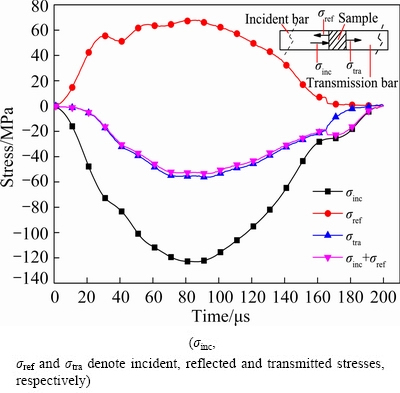
Fig. 3 Dynamic stress equilibrium of typical SHPB test
It is notable that the test must be under the one-dimensional condition, that is, the sample and bars (incident bar and transmission bar) should be on the same axis. Figure 3 shows that the dynamic stress on the transmission bar, which is the sum of the incident and reflected stresses, is absolutely equal to the dynamic stress transmitted on the other side. Besides, it is necessary to ensure that the air pressure and position of the spindle punch in each experiment are the same. Based on the one-dimensional stress wave theory, the incident energy, Einc, reflected energy, Eref, and transmitted energy, Etra, could be respectively obtained through the incident stress, σinc(t), the reflected stress, σref(t), and the transmitted stress, σtra(t), by the following formulas [29]:
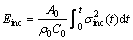 (1)
(1)
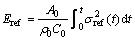 (2)
(2)
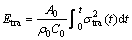 (3)
(3)
where A0 is the cross-sectional area of the elastic bar, ρ0 is the density of the bar, C0 is the longitudinal wave velocity of the bar and t is the time.
According to the energy conservation law, the total input energy, which equals the incident energy, is the sum of output energy of five parts:
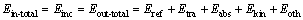 (4)
(4)
where Eabs, Ekin and Eoth, respectively, are the absorbed energy, the kinetic energy of the rock sample and the other dissipated energy, such as the energy loss between the contact surface of the rock and bar; Ein-total and Eout-total are the total incident and output energy during the experiment, respectively. As ZHANG et al [30] confirmed, the kinetic energy of the sample is small, no more than 5% of the incident energy; meanwhile, the other dissipated energy which is less than the kinetic energy can thus be ignored in this work, as shown in Fig. 4. So, after eliminating the kinetic energy and the other dissipated energy, Eq. (4) is simplified:
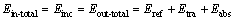 (5)
(5)
From Eq. (5), the absorbed energy can be obtained by
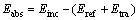 (6)
(6)
In addition, according to LI et al [31], energy dissipation consists of three parts, namely breakage energy dissipation, motion energy dissipation and others such as thermal energy and friction energy. The energy dissipation means energy dissipation of absorbed energy in this work. Because breakage energy dissipation accounts for almost 85% of the total, the remaining two parts are treated to be equal. Thus, the absorbed energy causing damage and breakage of the rock can be calculated by Eq. (6).
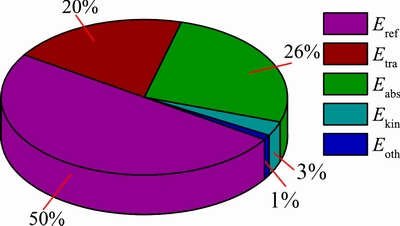
Fig. 4 Diagram of energy dispassion
For cyclic impact experiment, the total energy is accumulated by the input energy of every impact times; that is, the total energy is equal to the sum of incident energy in every impact test, as shown in Eq. (7). And the total reflected, absorbed, and transmitted energy are the sum of the reflected, transmitted and absorbed energy in every impact test, respectively, as given in Eqs. (8), (9) and (10):
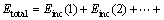
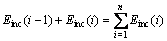 (7)
(7)
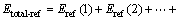
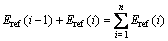 (8)
(8)
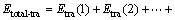
 (9)
(9)
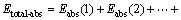
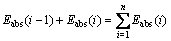 (10)
(10)
where Etotal, Etotal-ref, Etotal-tra and Etotal-abs are the total energy, the total reflected energy, the total transmitted energy and the total absorbed energy, respectively; n stands for the impact times.
The energy dispassion rates under the impact loading including the rate of reflected, transmitted and absorbed energy can be calculated by
 (11)
(11)
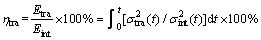 (12)
(12)
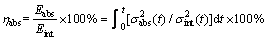 (13)
(13)
where ηref, ηtra and ηabs are the rates of reflected, transmitted and absorbed energy under the impact loading, respectively. And the total energy dispassion rate under the cyclic impact loading can be expressed as follows:
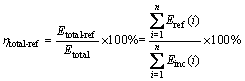 (14)
(14)
 (15)
(15)
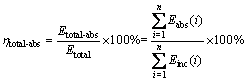 (16)
(16)
where ηtotal-ref, ηtotal-tra and ηtotal-abs are the rates of the total reflected, transmitted and absorbed energy, respectively.
The accumulated absorbed energy per volume can be obtained by
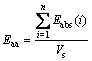 (17)
(17)
where Eaa is the accumulated absorbed energy per volume and Vs is the volume of the rock sample.
4 Experimental results and analysis
The typical waves of different heat-treated rocks under cyclic impact loading are shown in Fig. 5. And the curves of the energy dissipation of rocks treated at various temperatures under cyclic impact loading are shown in Fig. 6.
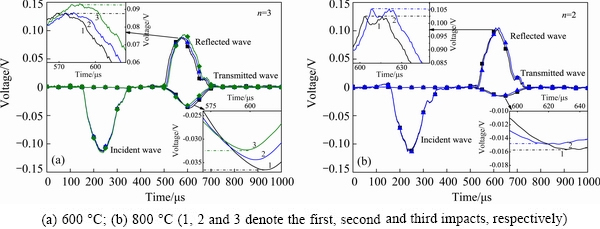
Fig. 5 Typical curves of heat-treated granite under cyclic impact loading
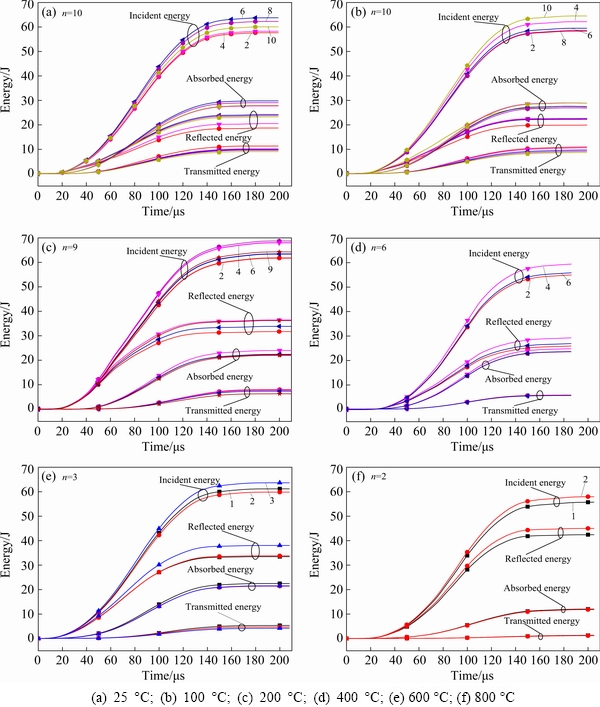
Fig. 6 Energy dissipation of heat-treated granite under cyclic impact loading
With the increasing impact times, the same phenomenon occurs for rocks treated at 600 and 800 °C. The amplitude of the reflected wave increases gradually and the peak value appears later than the previous cycle. On the contrary, the amplitude of the transmitted wave decreases with the increasing impact times, yet the peak value appears earlier than the original one. Because of nearly the same incident wave, namely, the same incident energy, the variation of the reflected and transmitted wave is also a response of energy dissipation. The impact process is a process of energy exchange between the rock and exterior.
Certainly, there is an energy exchange accompanied by deformation during the impact process. Under cyclic impact loading, the transmitted energy, like the peak stress, is related to the incident energy. Although samples are not destroyed before the final cycle, experimental results can also reflect the mechanical properties of the sample to a certain extent. For rocks treated at various temperatures from 25 to 800 °C, the slope of the elastic stage, namely the elastic modulus, presents a declining trend as the impact times increases. That is to say, with the growing impact times, the elastic energy is finally dissipated. As previously confirmed, the interior structure of the rock changes markedly with the rising temperature [32]. By using scanning electron microscopy (SEM), it is found that holes, cracks, transcrystalline cracks and thermal melting micro-pores emerge gradually with the increasing temperature. Owing to the rising temperature, the number and average opening distance of the microcracks increase [33]. Thus, the elastic modulus presents a declining trend and the elastic energy dissipates with the increasing impact times.
As shown in Fig. 6, for rocks treated at low temperature (25 or 100 °C), the reflected energy is less than the absorbed energy. However, with the rising temperature, the reflected energy grows gradually, and finally exceeds the absorbed energy. The reflected energy under the first impact goes up with the rising temperature, but the transmitted energy and absorbed energy follow different change laws compared with the reflected energy, decreasing with the rising temperatures.
4.1 Energy dissipation
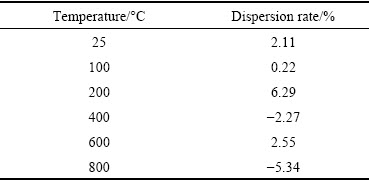
For the cyclic impact experiment, the incident wave, namely the incident energy, must be consistent. Although the incident energies for the experimental temperatures varying from 25 to 800 °C are not the same, the values of them are all around 60 J and the dispersion rate is no more than 5% except for the incident energy at 200 and 800 °C, as shown in Fig. 7. Furthermore, the incident energy for the same experimental temperature is nearly the same, presenting a little discreteness. Hence, although the incident energy presents a little difference, the experiment results are reliable. The dispersion rates corresponding to varying temperatures are given in Table 2.
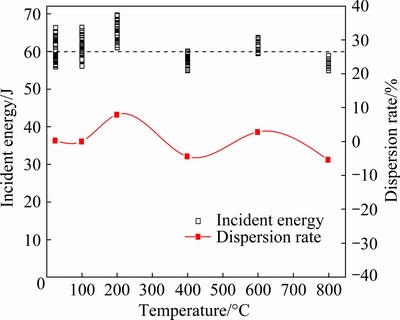
Fig. 7 Incident energy and dispersion rate at different temperatures
Table 2 Dispersion rates for varying temperatures
Besides, in order to understand the thermal effect on the energy dissipation under the cyclic impact loading clearly and reduce the error caused by experiment as far as possible, the final energy could be expressed as follows:
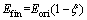 (18)
(18)
where Efin is the final energy expressed by Eq. (18); Eori is the energy of original experiment including incident, reflected, transmitted and absorbed energy; ξ stands for the dispersion rate. After the transformation by Eq. (18), the final incident energy is equal to the target incident energy, Etar-inc, which is 60 J.
4.1.1 Correlation between energy dissipation and temperature
The varying correlation between the energy dissipation at the first impact and different temperatures is shown in Fig. 8. When the temperature increases, the reflected energy under the first impact increases accordingly; on the contrary, the absorbed energy and transmitted energy under the first impact all show decreasing trend with different changing laws. As is known, absorbed energy is very effective when being used to break rock. Because the interior structure of rock is damaged gradually with the rising temperature, less absorbed energy is needed to destroy the rock treated at higher temperature. Hence, the absorbed energy and transmitted energy under the first impact decrease with the rising temperature.
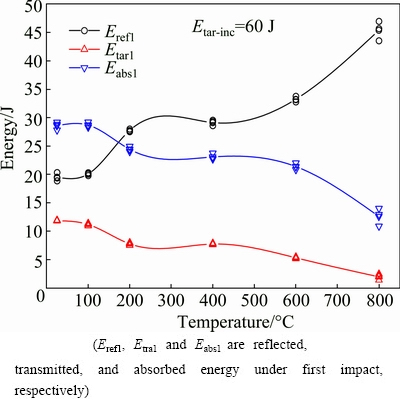
Fig. 8 Correlation between energy dissipation under first impact and temperature
Figure 9 shows the correlation between the total energy dissipation and temperature. Similar to the absorbed and transmitted energy under the first impact, the total absorbed energy and transmitted energy decrease with the increasing temperature. When the temperature exceeds 200 °C, different phenomenon comes out to the total reflected energy compared to the reflected energy under the first impact; that is to say, the total reflected energy decreases gradually. The main reason for the difference is that the total incident energy of rock treated at lower temperature is much larger than that of rock treated at higher temperature. Below 200 °C, the reflected energy under the first impact is smaller than the absorbed energy under the first impact. However, the reflected energy under the first impact is larger than the absorbed energy under the first impact when the temperature reaches or exceeds 200 °C. At this time, there are a lot of cracks in the interior of the rock sample. The same phenomenon comes to the total reflected energy.
In detail, when the temperature is below 100 °C, dehydration takes place in holes in the interior of the rock, and the interior structure changes accordingly. When the temperature continues to increase to above 100 °C, some small fissures gradually develop into larger fissures which are difficult to restore the original shape even after cooling. Meanwhile, the mineral composition and interior structure of the granite change obviously at high temperature. For example, some of the mineral substances contained in granite which are easily melted, decompose and evaporate, causing the number and sizes of cracks to increase at high temperature. In addition, the pre-cracks continue to extend at high temperature. Therefore, the absorbed energy and transmitted energy show decreasing trend with the rising temperature, while the reflected energy under the first impact increases with the rising temperature.
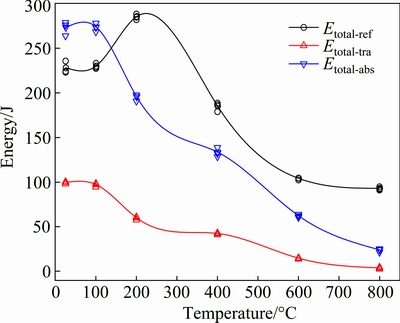
Fig. 9 Correlation between total energy dissipation and temperature
As shown in Fig. 10, due to the same incident energy at every impact, the ηtra1, ηtotal-tra, ηabs1 and ηtotal-abs decrease accordingly. The more the cracks and interfaces at high temperature, the greater the rate of reflected energy, and thus ηref1 and ηtotal-ref increase with the rising temperature. The correlation between the energy dissipation rate and temperature could be described by linear equation as follows:
 (19)
(19)
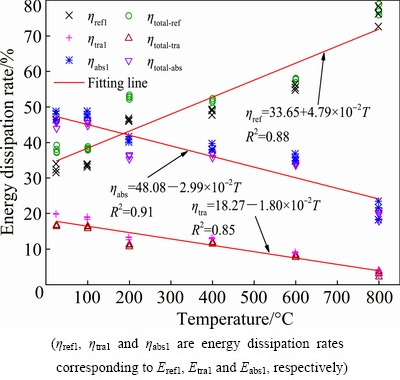
Fig. 10 Correlation between energy dissipation rate and temperature
4.1.2 Correlation between energy dissipation and impact times
It is noteworthy that the reflected energy shows an increasing trend with the increase of impact times, while the transmitted energy and absorbed energy show an opposite variation, as shown in Fig. 11.
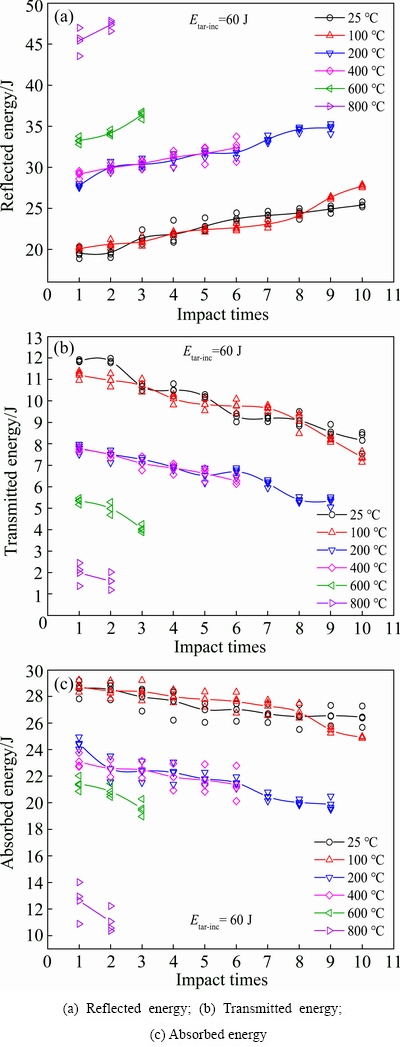
Fig. 11 Correlation between energy dissipation and impact times
The change of the interior structure of rock caused by the increasing impact times, such as the increasing number and sizes of cracks, finally causes the transmitted and absorbed energy to decrease and the reflected energy to increase gradually at the same time. In the whole impact experiments, the transmitted energy is small. For rock that undergoes the same cyclic impact loading, the reflected, transmitted energy and absorbed energy are also different with the rising temperature.
4.2 Thermal effect on impact times and accumulated absorbed energy per volume
As shown in Fig. 12, the impact times decreases linearly as the temperature increases. When the temperature increases, the interior structure of rock is damaged gradually, which leads to less absorbed energy needed to destroy the rock sample. Meanwhile, the incident energy of every impact is almost the same, so less impact times is needed to destroy the sample with the rising temperature. The correlation between the impact times and temperature agrees well with the linear equation:
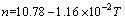 (20)
(20)
Because the damage accumulates with the increase of impact times, the number, length and width of the cracks increase accordingly, and the accumulated absorbed energy increases with the growing impact times. Then, the accumulated absorbed energy per volume increases gradually, as shown in Fig. 13.
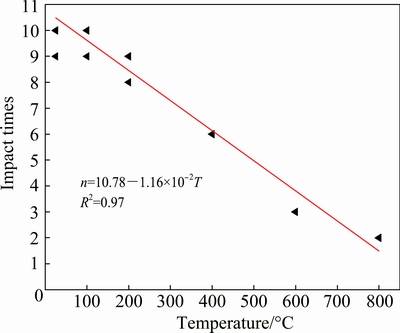
Fig. 12 Correlation between impact times and temperature
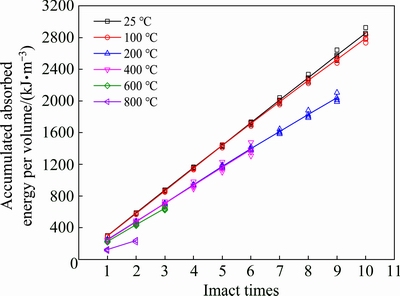
Fig. 13 Correlation between accumulated absorbed energy per volume and impact times
Figure 14 shows the correlation between the accumulated absorbed energy per volume and temperature. Due to the damage of the interior structure of the rock at high temperature, less absorbed energy is needed to destroy the sample, hence the accumulated absorbed energy per volume decreases with the rising temperature. The linear correlation can be described by the following equation:
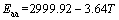 (21)
(21)
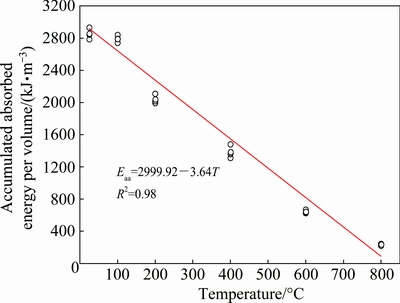
Fig. 14 Correlation between accumulated absorbed energy per volume and temperature
4.3 Correlation between absorbed energy and failure mode
It has been stated that the slenderness ratio has an effect on the failure modes of rock [34,35]. The size effects on the rock’s mechanical characteristics are very complicated, because of the variations in the composition and structure of different rocks. That is to say, even at the same slenderness ratio, the development and extent of microcracks and their distribution can be different for different types of rocks [36,37]. However, different from the size effects, the effect of energy dissipation on the failure modes of a rock is the same for different types of rocks. So only one type of rock (granite) was chosen. Furthermore, in order to study the effect of absorbed energy on the failure modes of the rock, the same slenderness ratio (1) and incident energy (60 J) were chosen. Temperature plays a very important role in affecting the fracture of rock [38]. Different temperatures result in different impact times, and thus different absorbed energy. Due to high temperature, less absorbed energy is needed to destroy the rock sample, hence the total absorbed energy decreases gradually with the rising temperature, as shown in Fig. 9. At high temperature, even though the total absorbed energy is low, the sample breaks into powder, as shown in Fig. 15.

Fig. 15 Real-time failure photos of heat-treated granite samples
The rocks finally fail after several impacts but show major differences with the rising temperature. When the temperature is below 200 °C, the failure mode is the same, and the rock breaks along a main failure path. As the temperature continues to increase, reaching 200 °C, there are two or more apparent failure paths. The greatest difference appears above 400 °C, and the rock breaks into powder and some small patches at 600 °C. The main failure paths can still be seen from the real-time failure photos. When the temperature is higher, reaching 800 °C, the rock breaks into powder with no clear main failure path as seen in the real-time failure photos. Because of the large number of weakened interfaces, when the rock heat-treated at high temperature (800 °C) absorbs enough energy, the rock breaks into powder with no clear main failure path. Owing to the increasing temperature, the interior structure of the rock incurs varying degrees of damage. In other words, when the temperature increases, the pores, microcracks and fissures all increase accordingly. As XU et al [39] confirmed, rock porosity increases with the rising temperatures. This is to say, the weakening of the interior structure of the rocks is more serious when the temperature increases. Therefore, less absorbed energy is needed and then the different failure modes emerge.
As shown in Fig. 16, the density of the rock prior to thermal treatment presents some differences but the fluctuation is small. The variation in the density of the rock after thermal treatment may, to some degree, reflect the changes in the interior structure. With the rising temperature, the density decreases with a nonlinear trend. Especially when the temperature reaches 600 and 800 °C, the range of decreasing density clearly becomes large.
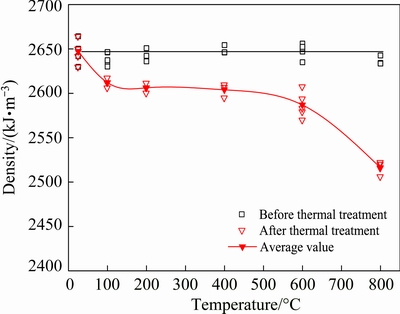
Fig. 16 Correlation between density and temperature
The density changes following the volume and quality. When the temperature is below 200 °C, the water contained in the rock evaporates. As a result, the quality decreases and the volume is almost unchanged. Therefore, the density decreases accordingly. But, when the temperature continues to increase, reaching 200 °C or higher, the thermal stress leads to the increase of the number of pores, microcracks and fissures, and some mineral particles begin to melt and decompose at high temperature. Particularly when the temperature is 800 °C, the function of thermal stress shows even more clearly. These are the reasons that the quality decreases and volume increases at the same time. So, the higher the temperature, the lower the density [40], and the larger the porosity [41]. Furthermore, with the increasing temperature, the density decreases with an accelerating trend. The change of the density with the rising temperature leads to the change of the mechanical properties of rock, which finally affects the energy dissipation and failure mode of the rock.
5 Discussion
According to the results above, it is obvious that the different energy dissipation of rocks indeed results from the varying temperature. In this work, although the samples were sourced from the same rock mass, variations in the results, to some extent, still occurred, which may be due to differences in terms of inhomogeneity and moisture conditions in the samples. Meanwhile, in the test process, the rock sample may be reabsorbed from the atmosphere. However, the variation is small and can be ignored.
The energy is dissipated in the form of wave propagation in the rock sample. Here, a simplified graph of wave propagation in the interior of the sample is shown in Fig. 17. There are several pores and microcracks in the sample. When the energy propagates in the rock sample in the form of a wave, the wave propagation can be divided into three different forms: perpendicular to the interface of the microcrack (I), oblique to the interface of the microcrack (II), and parallel to the interface of the microcrack (III). As can be seen in Fig. 17, when the incident wave comes across the microcrack, that is, the incident energy comes across the microcrack, the three components of the energy are divided, namely, the absorbed energy, reflected energy and transmitted energy. The same condition occurs in the two interfaces of the microcrack. In the first propagation form (I), the reflected energy propagates along the opposite direction to that of the incident energy. And, the reflected energy propagates along the direction which is at a certain angle to the incident direction in the second propagation form (II). When it comes to the third propagation form (III), there is no reflected energy. The absorbed energy is used to break the sample. Thus, when the absorbed energy is high enough, the rock sample will be broken after several instances of energy propagation in the above forms.
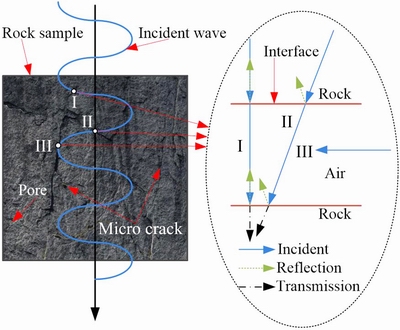
Fig. 17 Graph of wave propagates in interior of rock
6 Conclusions
(1) When the temperature increases, the reflected energy increases accordingly and finally exceeds the absorbed energy at 200 °C. Both the absorbed energy under the first impact and the total absorbed energy decrease with the rising temperature, and the same phenomenon appears for the transmitted energy under the first impact and the total transmitted energy.
(2) The reflected energy under the first impact increases with the rising temperature, but the total reflected energy decreases after 200 °C. The rates of both transmitted energy and absorbed energy decrease when the temperature increases. However, the rates of the reflected energy under the first impact and the total reflected energy increase with the rising temperature.
(3) The impact times decreases with the increasing temperature. The accumulated absorbed energy per volume increases when the impact times increases but decreases when the temperature increases. After treatment at high temperature, although the absorbed energy is low, the sample breaks thoroughly. Especially when the temperature is 800 °C, the sample breaks into powder.
(4) The deep rock mass is unable to bear much dynamic disturbances. In order to ensure the stability of the surrounding rock, the dynamic disturbance should be reduced as much as possible.
References
[1] TAO Ming, LI Xi-bing, LI Di-yuan. Rock failure induced by dynamic unloading under 3D stress state [J]. Theoretical and Applied Fracture Mechanics, 2013, 65(3): 47-54.
[2] LI Xi-bing, DU Kun, LI Di-yuan. True triaxial strength and failure modes of cubic rock specimens with unloading the minor principal stress [J]. Rock Mechanics and Rock Engineering, 2015, 48(6): 2185-2196.
[3] YIN Tu-bing, SHU Rong-hua, LI Xi-bing, WANG Pin, LIU Xi-ling. Comparison of mechanical properties in high temperature and thermal treatment granite [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(7): 1926-1937.
[4] CHAKI S, TAKARLI M, AGBODJAN W P. Influence of thermal damage on physical properties of a granite rock: Porosity, permeability and ultrasonic wave evolutions [J]. Construction and Building Materials, 2008, 22(7): 1456-1461.
[5] YAVUZ H, DEMIRDAG S, CARAN S. Thermal effect on the physical properties of carbonate rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(1): 94-103.
[6] WANG Pin, YIN Tu-bing, LI Xi-bing, ZHANG Shuai-shuai, BAI Lv. Dynamic properties of thermally treated granite subjected to cyclic impact leading [J]. Rock Mechanics and Rock Engineering, DOI: http://doi.org/10.1007/s00603-018-1606-y.
[7] TIAN H, ZIEGLER M, KEMPKA T. Physical and mechanical behavior of claystone exposed to temperatures up to 1000 °C [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 144-153.
[8] LIU Shi, XU Jin-yu. Mechanical properties of Qinling biotite granite after high temperature treatment [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 71: 188-193.
[9] LIU Shi, XU Jin-yu. An experimental study on the physico- mechanical properties of two post-high-temperature rocks [J]. Engineering Geology, 2015, 185: 63-70.
[10] YIN Tu-bing, BAI Lv, LI Xi-bing, ZHANG Shuai-shuai. Effect of thermal treatment on the mode I fracture toughness of granite under dynamic and static coupling lead [J]. Engineering Fracture Mechanics, 2018, 199: 143-158.
[11] ZHANG Z X, YU J, KOU S Q, LINDQVISTET P A. Effects of high temperatures on dynamic rock fracture [J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(2): 211-225.
[12] YIN Tu-bing, WANG Pin, LI Xi-bing, WU Bang-biao, TAO Ming, SHU Rong-hua. Determination of dynamic flexural tensile strength of thermally treated Laurentian granite using semi-circular samples [J]. Rock Mechanics and Rock Engineering, 2016, 49(10): 3887-3898.
[13] PAVLOVIC M N. Fracture mechanics of concrete: Applications of fracture mechanics to concrete, rock and other quasi-brittle materials [J]. Engineering Structures, 1996, 18(1): 887-888.
[14] HUDSON J A, BROWN E T, FAIRHURST C. Shape of the complete stress-strain curve for rock [C]//Stability of Rock Slopes. New York: ASCE, 1972: 773-795.
[15] JU Yang, WANG Hui-jie, YANG Yong-ming, HU Qin-ang, PENG Rui-dong. Numerical simulation of mechanisms of deformation, failure and energy dissipation in porous rock media subjected to wave stresses [J]. Science China Technological Sciences, 2010, 53(4): 1098-1113.
[16] SONG Da-zhao, WANG En-yuan, LI Zhong-hui, LIU Jie, XU Wen-quan. Energy dissipation of coal and rock during damage and failure process based on EMR [J]. International Journal of Mining Science and Technology, 2015, 25(5): 787-795.
[17] CAO wen-zhuo, LI Xi-bing, ZHOU Zi-long, YE Hai-wang, WU Hao. Energy dissipation of high-stress hard rock with excavation disturbance [J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2759-2767. (in Chinese)
[18] YIN Tu-bing, LI Xi-bing, YE Zhou-yuan, GONG Feng-qiang, ZHOU Zi-long. Energy dissipation of rock fracture under thermo- mechanical coupling and dynamic disturbances [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(6): 1197-1202. (in Chinese)
[19] BAGDE M N, PETROS V. Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2): 237-250.
[20] YIN Tu-bing, ZHANG Shuai-shuai, LI Xi-bing, BAI Lv. A numerical estimate method of dynamic fracture initiation toughness of rock under high temperature [J]. Engineering Fracture Mechanics, 2018, 204: 87-102.
[21] REN Xing-tao, ZHOU Ting-qing, ZHONG Fang-ping, HU Yong-le, WANG Wan-peng. Experimental study for the dynamic mechanical behavior of granite [J]. Journal of Experimental Mechanics, 2010, 25(6): 723-730. (in Chinese)
[22] ZHU Ze-qi, SHENG Qian, LENG Xian-lun, ZHU Fu-guang. Experimental study of dynamic mechanical property of Dagangshan granite [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3469-3474. (in Chinese)
[23] ZHANG Ping, XU Jian-guang, LI Ning. Fatigue properties analysis of cracked rock based on fracture evolution process [J]. Journal of Central South University of Technology, 2008, 15(1): 95-99.
[24] XIAO Jian-qing, DING De-xin, JIANG Fu-liang, XU Gen. Fatigue damage variable and evolution of rock subjected to cyclic loading [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(3): 461-468.
[25] JIA Chao-jun, XU Wei-ya, WANG Ru-bin, WANG Wei, ZHANG Jiu-chang, YU Jun. Characterization of the deformation behavior of fine-grained sandstone by triaxial cyclic loading [J]. Construction and Building Materials, 2018, 162: 113-123.
[26] BIENIAWSKI Z T, BERNED M J. Suggested methods for determining the uniaxial compressive strength and deformability of rock materials: Part 1. Suggested method for determining deformability of rock materials in uniaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1979, 16(2): 138-140.
[27] ZHOU Y X, XIA K, LI X B, MA G W, ZHAO J, ZHOU Z L, DAI F. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 49(1): 105-112.
[28] LI Xi-bing, LOK T S, ZHAO Jian. Dynamic characteristics of granite subjected to intermediate loading rate [J]. Rock Mechanics and Rock Engineering, 2005, 38(1): 21-39.
[29] LI Xi-bing. Rock dynamics fundaments and applications [M]. Beijing: Science Press, 2014. (in Chinese)
[30] ZHANG Z X, KOU S Q, JIANG L G, LINDQVISTET P A. Effects of loading rate on rock fracture: fracture characteristics and energy partitioning [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 745-762.
[31] LI Ming, MAO Xian-biao, LU Ai-hong, TAO Jing, ZHANG Guang-hui, ZHANG Lian-ying, LI Chong. Effect of sample size on energy dissipation characteristics of red sandstone under high strain rate [J]. International Journal of Mining Science and Technology, 2014, 24(2): 151-156.
[32] XU Xi-li, KANG Zong-xin, JI Ming, GE Wen-xuan, CHEN Jing. Research of microcosmic mechanism of brittle-plastic transition for granite under high temperature [J]. Procedia Earth and Planetary Science, 2009, 1(1): 432-437.
[33] NASSERI M H B, SCHUBNEL A, YOUNG R P. Coupled evolutions of fracture toughness and elastic wave velocities at high crack density in thermally treated westerly granite [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(4): 601-616.
[34] KRAUTHAMMER T, ELFAHAL M M, LIM J, OHNO T, BEPPU M, MARKESET G. Size effect for high-strength concrete cylinders subjected to axial impact [J]. International Journal of Impact Engineering, 2003, 28(9): 1001-1016.
[35] HONG L. Size effect on strength and energy dissipation in fracture of rock under impact loads [D]. Changsha: Central South University, 2008. (in Chinese)
[36] DARLINGTON W J, RANJITH P G, CHOI S K. The effect of sample size on strength and other properties in laboratory testing of rock and rock-like cementitious brittle materials [J]. Rock Mechanics and Rock Engineering, 2011, 44(5): 513-529.
[37] SU Hai-jian, JING Hong-wen, MAO Xiao-biao, ZHAO Hong-hui, YIN Qian, WANG Chen. Size effect of sandstone after high temperature under uniaxial compression [J]. Journal of Central South University, 2015, 22(5): 1901-1908.
[38] WANG Xi-shu, WU Bi-sheng, WANG Qing-yuan. Online SEM investigation of microcrack characteristics of concretes at various temperatures [J]. Cement and Concrete Research, 2005, 35(7): 1385-1390.
[39] XU Xiao-li, GAO Feng, SHEN Xiao-ming, XIE He-ping. Mechanical characteristics and microcosmic mechanisms of granite under temperature loads [J]. Journal of China University of Mining and Technology, 2008, 18(3): 413-417.
[40] DAVID C, MENENDEZ B, DAROT M. Influence of stress-induced and thermal cracking on physical properties and microstructure of La Peyratte granite [J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(4): 433-448.
[41] YAVUZ H, DEMIRDAG S, CARAN S. Thermal effect on the physical properties of carbonate rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(1): 94-103.
舒荣华1,尹土兵1,李夕兵1,殷志强2,唐礼忠1
1. 中南大学 资源与安全工程学院,长沙 410083;
2. 安徽理工大学 深部煤矿采动响应与灾害防控安徽省重点实验室,淮南 232001
摘 要:深部采矿中高温导致岩石产生热损伤。为了了解循环冲击作用下热处理对岩石能量耗散的影响,运用霍普金森实验系统进行热处理后岩石的循环冲击加载实验,分析能量耗散、能量耗散率、冲击次数、单位体积能耗以及破坏模式与温度之间的关系。实验结果表明:第一次冲击的反射能随着温度的升高逐渐增大并且最终超过吸收能,然而,总反射能在200 °C后随着温度的升高逐渐减小;第一次冲击的吸收能与总吸收能随着温度的升高逐渐减小,能量吸收率也相应减小;与吸收能表现出相似的规律,随着温度的升高,第一次冲击的透射能与总透射能逐渐减小,能量透射率也随之减小,相反地,能量反射率却逐渐增大。随着温度的升高,岩石破坏所需的冲击次数逐渐减少;另外,当岩石经受不同热处理后,其破坏模式也有所不同,即:当温度高时,尽管吸收的能量低,岩石试样在经过几次冲击后破碎成粉状。
关键词:能量耗散;花岗岩;循环冲击;压缩;热处理
(Edited by Bing YANG)
Foundation item: Project (2016YFC0600706) supported by the State Key Research Development Program of China; Projects (41630642, 51774325) supported by the National Natural Science Foundation of China; Project (2017JJ3389) supported by the Natural Science Foundation of Hunan Province, China; Projects (2017CX006, 2018zzts212) supported by the Innovation-Driven Program of Central South University, China
Corresponding author: Tu-bing YIN; Tel: +86-18684770361; E-mail: tubing_yin@csu.edu.cn
DOI: 10.1016/S1003-6326(19)64948-4

