J. Cent. South Univ. (2012) 19: 703-708
DOI: 10.1007/s11771-012-1060-z
Development and experimental validation of a one-dimensional
dynamic hygrothermal modeling based on air humidity ratio
GUO Xing-guo(郭兴国)1, CHEN You-ming(陈友明)2, DENG Yong-qiang(邓永强)2
1. School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China;
2. College of Civil Engineering, Hunan University, Changsha 410082, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: A modified one-dimensional transient hygrothermal model for multilayer wall was proposed using air humidity ratio and temperature as the driving potentials. The solution for the governing equations was obtained numerically by implementing the finite-difference scheme. To evaluate the accuracy of the model, a test system was built up to measure relative humidity and temperature within a porous wall and compare with the prediction of the model. The prediction results have good agreement with the experimental results. For the interface close to indoor side, the maximum deviation of temperature between calculated and test data is 1.87 K, and the average deviation is 0.95 K; the maximum deviation of relative humidity is 11.4%, and the average deviation is 5.7%. For the interface close to outdoor side, the maximum deviation of temperature between prediction and measurement is 1.78 K, and the average deviation is 1.1 K; the maximum deviation of relative humidity is 9.9%, and the average deviation is 4.2%.
Key words: transient hygrothermal modeling; air humidity ratio; modified modeling; experimental test; multilayer wall
1 Introduction
In hot and humid climate of south China, the trend toward the construction of more energy efficient buildings in recent years has increased the concern about the presence of moisture in wall cavities. One of the widespread problems with residences is the damage caused as a direct or indirect result of moisture transfer at the building envelope. Because of the large difference between indoor and outdoor temperature and high indoor humidity, condensation in residential buildings during winter is very common. Moisture accumulation within the material of a building envelope can lead to poor thermal performance of the envelope, degradation of organic materials, metal corrosion, and structure deterioration. Therefore, in south China, the investigation of heat and moisture transfer in porous building materials is extremely important not only for the characterization of behavior in connection with durability, waterproofing, and thermal performance, but also avoiding health risk due to the growth of microorganisms.
Combined heat and moisture transfer research started as a separate research topic in the 1930s. The most common and accepted model is the Philip and de VRIES model [1], which uses the temperature and moisture content gradients as the driving potentials. Since moisture content is not a continuous potential, there is discontinuity on the moisture content profile at the interface between two porous media, due to their different hygroscopic behaviors. The problem of discontinuity was solved by using relative humidity or capillary pressure as driving potentials, such as PEDERSEN [2] and K?NZEL [3]. However, the use of capillary suction pressure as a potential is problematic because it is difficult to directly measure and some coefficients are difficult to obtain. Another disseminated and accepted model is LUIKOV model [4]. The conservation equations include mass, momentum, and energy conservation equations. But the solutions are either numerical or complicated involving complex eigenvalues and it also leaves the problem of determining material properties. In the building application, many researchers adopted some assumptions to obtain the linear property of the system equations and make it possible to use an analytical solution, mainly including a constant gas pressure as the atmospheric pressure throughout porous media, and constant material properties [5-6]. The analytical solution is simple to calculate. However, if the material properties of building materials are not constant and vary greatly with environmental parameters, the coupled system is non-linear and only numerical soluble. BUDAIWI et al [7] proposed a dynamic heat and mass transfer model for non-cavity wall. Both heat and moisture transfer were simultaneously considered and their interactions were also modeled. But the model neglected the liquid transfer, which limited itself to low moisture content range and no experimental validation under natural climatic boundary conditions was provided. Recently, a transient heat, air and moisture transfer model is developed based on basic conservation of mass and energy equations [8]. A mathematical model to describe the heat, air and moisture transfer in hollow bricks was developed in Ref. [9].
This work constitutes part of an ongoing research project investigating heat and moisture transfer in building structures of south China, both experimentally and numerically. One of the main objectives of this work is to extend BUDAIWI model to high moisture content by considering the liquid transfer. The other objective is to build up an experimental test system to evaluate the accuracy of the model.
2 Mathematical modeling
2.1 Model development
The model presented in this work is derived from conservation of mass and energy flow in a one-dimensional element volume of porous material. The phase change occurring within material acts as a heat source or sink, which results in the coupled relationship between heat transfer and moisture transfer. The model is mainly based on the assumptions as shown in Ref. [7].
Air humidity ratio, W, is the mass of moisture per unit mass of air in building porous materials, which is the function of the material moisture content, U, and temperature, T:
 (1)
(1)
The partial derivative of W with respect to t is
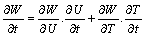 (2)
(2)
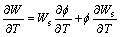 (3)
(3)
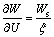 (4)
(4)
where f is relative humidity, Ws is saturation air moisture content, t is time, ξ is slope of moisture equilibrium curve.
Analogy to the heat balance equation, the moisture balance equation can be expressed as
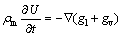 (5)
(5)
where
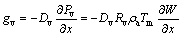 (6)
(6)
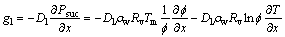 (7)
(7)
Substituting Eq. (3) into Eq. (7), then
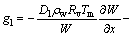
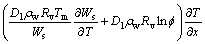 (8)
(8)
where Dv is material vapor diffusion coefficient, Dl is material liquid permeability coefficient, Rv is water vapor characteristic constant, ρa is air density, ρm is material density, and Tm is material temperature.
The second term on the right side of Eq. (8) describes the capillary transport based on a temperature gradient. Under practical conditions, it is small compared with the first term [3]. Therefore, it can be disregarded. Then, Eq. (8) becomes
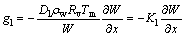 (9)
(9)
Liquid transport rate can also be written as
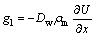 (10)
(10)
Then, we may obtain that
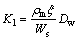 (11)
(11)
where Dw is material liquid diffusivity coefficient which strongly depends on the moisture content and can be written as Dw=aexp(bCm) [10]. Parameter Cm is volumetric moisture capacity which can be written as
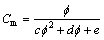
and a, b, c, d and e are constants determined by experiment.
Substituting gl and gv into Eq. (5), then
 (12)
(12)
By substituting Eqs. (3), (4) and (12) into Eq. (2), it becomes
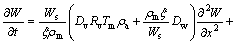
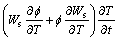 (13)
(13)
According to the result of IEA Annex 24 [11], we may obtain that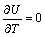 . And hence
. And hence 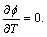
Then, Eq. (13) becomes
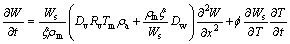 (14)
(14)
The corresponding boundary conditions at both sides of a wall can be written as
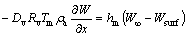 (15)
(15)
The saturated air humidity ratio, Ws, can be expressed as
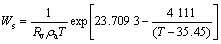 (16)
(16)
And hm is related to surface heat transfer coefficient hc through the Lewis relation. The heat transport process through a porous material slab can be generally described by [12]
 (17)
(17)
The corresponding boundary conditions at interior surface of the wall can be written as
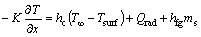 (18)
(18)
where Qrad is direct solar heat gain which can be calculated according to Ref. [13]. The radiation on the interior surfaces is not considered in this model, that is, Qrad=0. ms is the rate of mass transfer at wall surface which can be written as
 (19)
(19)
Therefore, the coupled heat and moisture transfer in a multilayer wall can be described by the governing Eqs. (14) and (17), and the corresponding boundary conditions are given by Eqs. (15) and (18).
2.2 Numerical solution
To ensure the numerical stability, the numerical resolution is based on the finite difference method with the implicit forward differences for time. At each time step, the moisture and heat transport equations are solved consecutively with a continuous update of the matrix coefficients by substituting the temperature and air humidity ratio until the convergence criteria are achieved. Given the hot humid climate conditions of south China, the wall may have high moisture content for a long time, therefore, the convergence criteria for the calculation of temperature and air humidity ratio can be expressed as [3]
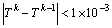 (20)
(20)
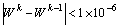 (21)
(21)
In order to evaluate the interstitial condensation, the air humidity ratio at each node is compared with the saturation value corresponding to the nodal temperature at the end of each time interval. If the value of the air humidity ratio is larger than the saturation value computed by Eq. (16), the air humidity ratio is set to the saturation value.
3. Experiment and comparisons
3.1 Experimental setup and test procedure
In order to validate the developed model, an experiment setup is built at Hunan University, China, to test the coupled heat and moisture transfer in a multilayer wall. Cross section of sample wall and sensor locations are shown in Fig. 1. The computational results are compared with the experimental results. The experimental setup and procedure are described as follows.
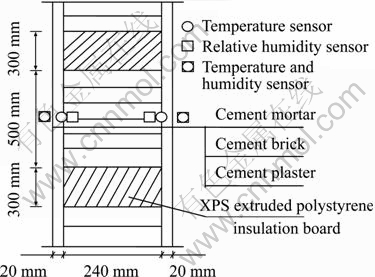
Fig. 1 Cross section of sample wall and sensor locations
The experimental setup is a 2 m?2 m?2 m rotary laboratory room surrounded by open areas. A multilayer wall sample is built at the centre of the south wall of the room. The sample wall has an area of 50 cm?50 cm and three layers with an external layer of 20 mm of cement mortar, a medium layer of 240 mm red brick (one brick thick) and an internal layer of 20 mm cement plaster. The outdoor surface of the tested wall directly exposes to the outdoor environment with variant temperature and air relative humidity, and its indoor surface is exposed to the indoor air. The upper and down of the tested walls were 300 mm XPS extruded polystyrene insulation board to insulation and resistance moisture. The indoor temperature is maintained at (23±2) °C by a room air-conditioner. Prior to the validation test, the tested wall is conditioned for a long period at the constant conditions of indoor temperature of 23 °C and indoor relative humidity of 60% to ensure a homogenous distribution of temperature and air humidity ratio.
Temperature and relative humidity sensors are located at the interfaces of common brick. To ensure that the test data accurately reflect one-dimensional heat and moisture transfer characteristics, temperature and relative humidity sensors are located at geometric center of the test wall as much as possible. Calibrated Pt100 is used to measure temperature of indoor air, outdoor air and the interfaces within the wall where the reading can directly be logged and displayed by a digital logger. HIH-4000 thermoset polymer capacitive sensor is used to measure relative humidity of indoor air, outdoor air and the interfaces within the wall, which has output signal of voltage. The relative humidity reading can be obtained from the relationship between relative humidity and voltage provided for each sensor by its supplier. Total six sensors for temperature and four sensors for relative humidity are installed for the experiment. A solar radiation meter is used to measure the global solar heat gain. A digital logger is used to log the experimental data with a sampling interval of 30 min. The tested wall samples, measurement instruments and experimental room are shown in Fig. 2.

Fig. 2 Tested wall sample (a) and measurement instruments (b)
3.2 Comparisons
The coupled heat and moisture transfer in the sample wall is predicted using the developed model under the experimental weather conditions. The initial and physical parameters used in the computation are determined according to the experimental conditions such as outdoor and indoor air temperature and relative humidity. The temperature and humidity ratio in the construction layers are initially assumed to be uniform. Its temperature is 23 °C and its humidity ratio is that at the relative humidity of 60%. The materials properties used in the computation are given in Table 1, which are obtained from Refs. [10, 14-15]. The heat transfer coefficients at inside and outside surfaces are 8.72 and 23.26 W/(m2·°C), respectively. The direct solar heat gain is obtained from measured global solar heat gain using the decomposing method presented by LAM and LI [16]. The mass transfer coefficients are obtained by LEWIS relation, considering the LEWIS number equal to 1. The time step in this calculation is 1 h. The outdoor and indoor conditions are the measured experimental conditions, as shown in Fig. 3 and Fig. 4. The measured global solar heat gain is shown in Fig. 5.
Table 1 Materials properties used in computation
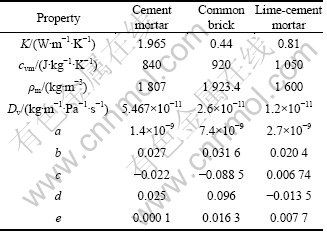

Fig. 3 Indoor and outdoor temperature
For the tested sample wall, its hygrothermal behavior is simulated over a period of seven days. Figures 6 and 7 illustrate the measured and predicted relative humidity at the two interfaces of the sample wall. It is shown that the predicted and measured values have a good agreement. For the interface close to outdoor side, compared with the experimental results, the maximum deviation of model predictions is 9.9% and the average deviation is 4.2%. For the interface close to indoor side, the maximum deviation is 11.4% and the average deviation is 5.7%. This difference might be due to the limitations in measurement precision and inaccuracy material properties. In addition, the precision of numerical method is another reason for this difference, e.g., the relative humidity calculation. The saturated air humidity ratio value calculated by Eq. (16) is lower than the true value. This may cause calculated value of the relative humidity ratio higher than the true value. Therefore, we may observe that the model predictions are slightly larger than the experimental values for most time.

Fig. 4 Indoor and outdoor relative humidity
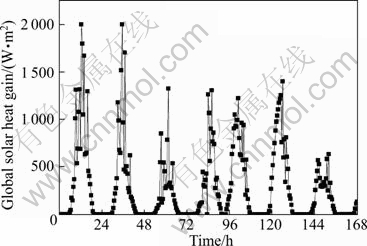
Fig. 5 Global solar heat gain
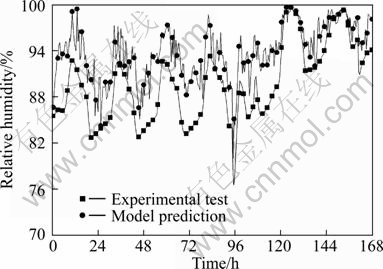
Fig. 6 Variation of relative humidity close to outdoor

Fig. 7 Variation of relative humidity close to indoor
The measured and predicted temperatures at various interfaces are shown in Figs. 8 and 9. The agreement between the predicted and experimental results is quite good. For the interface close to indoor side, the maximum deviation between calculated and test data is 1.87 K, and the average deviation is 0.95 K. For the interface close to outdoor side, the maximum deviation between prediction and measurement is 1.78 K, and the average deviation is 1.1 K. The error between the measured and predicted temperature is mainly caused by the imprecise irradiation measurements. The total irradiation used in the modeling for the south-facing wall is obtained by decomposing the total irradiation measured on horizon. The actual diffusive irradiation and ground reflection on south-facing wall are much stronger than those on horizon. This result in the measured temperature is higher than that predicted by the modeling. Also, the accuracy of the numerical model may cause this discrepancy.
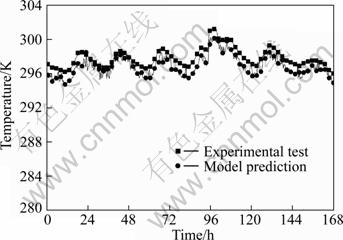
Fig. 8 Variation of temperature close to indoor
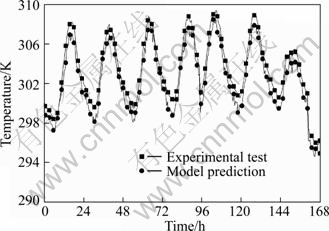
Fig. 9 Variation of temperature close to outdoor
4 Conclusions
1) Regarding air humidity ratio in building with porous material as a function of material moisture content and temperature, a modified BUDAIWI model is developed for evaluating the transient heat and moisture transfer behavior in building multilayer wall, in which liquid transfer and solar radiation are considered.
2) An experimental setup is built up to evaluate the correctness of the model. The air humidity ratio and temperature at the interfaces between two layers in multilayer wall are measured.
3) For the interface close to indoor side, the maximum deviation of temperature between calculated and test data is 1.87 K, and the average deviation is 0.95 K. The maximum deviation of relative humidity is 11.4%, and the average deviation is 5.7%.
4) For the interface close to outdoor side, the maximum deviation of temperature between prediction and measurement is 1.78 K, and the average deviation is 1.1 K. The maximum deviation of relative humidity is 9.9%, and the average deviation is 4.2%.
References
[1] PHILIP J R, DEVRIES D A. Moisture movement in porous materials under temperature gradients [J]. Transactions American Geophysical Union, 1957, 38(2): 222-232.
[2] PEDERSEN C R. Prediction of moisture transfer in building constructions [J]. Building and Environment, 1992, 33: 87-397.
[3] K?NZEL H M. Simultaneous heat and moisture transport in building components: One- and two-dimensional calculation using simple parameters [M]. Stuttgart: IRB Verlag, 1995: 63-69.
[4] LUIKOV A W. Heat and mass transfer in capillary-porous bodies [M]. Oxford, U.K: Pergamon, 1966: 87-92.
[5] CHEN You-ming, CHEN Zai-kang. The simultaneous heat and moisture transfer equations of porous building envelop and their linearization [J]. Journal of Basic Science Engineering, 1997, 5(2): 161-171.
[6] QIN Meng-hao, BELARBI R. Development of an analytical method for simultaneous heat and moisture transfer in building materials utilizing transfer function method [J]. Journal of Material Civil Engineering, 2005, 17(5): 492-497.
[7] BUDAIWI I., EI-DIASTY R, ABDOU A. Modelling of moisture and thermal transient behavior of multi-layer non-cavity walls [J]. Building and Environment, 1999, 34(5): 537-551.
[8] TARIKU F, KUMARAN K, FAZIO P. Transient model for coupled heat, air and moisture transfer through multilayered porous media [J]. International Journal of Heat and Mass Transfer, 2010, 53: 3035-3044.
[9] SANTOS G H D, MENDS N. Heat, air and moisture transfer through hollow porous blocks [J]. International Journal of Heat and Mass Transfer, 2009, 52: 2390-2398.
[10] KUMARAN M K. IEA-Annex 24, Task 3: Material Properties [M]. Canada: IRC/NRC, 1996: 30-103.
[11] HENS H. Heat, air and moisture transfer in insulated envelope parts. International energy agency (IEA), energy conservation in building and community systems, finial report, volume 1, task 1: Modeling [M]. IEA, Acco Leuven, 1996: 2-35.
[12] ANDESSON A C. Verification of calculation methods for moisture transport in porous building materials [M]. Stockholm: Swedish Council for Building Research, 1985: 23-26.
[13] American Society of Heating, Refrigerating, and Air-conditioning Engineers. ASHRAE handbook ? 2005 Fundamentals. [M]. Atlanta, GA Inc, 2005: 198-202.
[14] PEI Qing-qing, CHEN Zai-kang. An experimental study on isothermal moisture absorption and desorption processes of some common-used building materials [J]. Journal of Hunan University: Natural Science, 1999, 26(4): 96-99. (in Chinese)
[15] LI Kui-shan, ZHANG Xu, GAO Jun. Experimental investigation of hygrothermal parameters of building materials under isothermal conditions [J]. Journal of Building Physics, 2009, 32(4): 355-370.
[16] LAM J C, LI D H W. Correlation between global solar radiation and its direct and diffusion components [J]. Building and Environment, 1996, 31(6): 527-535.
(Edited by YANG Bing)
Foundation item: Project(51078127) supported by the National Natural Science Foundation of China; Project(JJ201109091631) supported by the Foundation for Young Scientists of Jiangxi Education Department, China
Received date: 2011-07-26; Accepted date: 2011-11-14
Corresponding author: CHEN You-ming, Professor, PhD; Tel: +86-731-88823515; E-mail: ymchen@hnu.edu.cn