基于TSVD-UKF的视觉/惯性融合位姿确定
宋申民,魏喜庆
(哈尔滨工业大学 控制理论与制导技术中心,黑龙江 哈尔滨,150001)
摘要:针对四自由度空间对接仿真平台定位和定姿问题,提出一种截断奇异值UKF(TSVD-UKF)算法用于视觉/惯性信息融合。由于EKF存在求解Jacobian矩阵困难以及线性化导致滤波不稳定等问题,提出利用具有更高精度和鲁棒性的UKF融合位姿确定算法。为了避免高维状态时UKF采样点集计算量过大,提出一种采用截断奇异值分解的采样点选取方法。实验验证结果表明:TSVD-UKF算法保证了导航精度的同时有效地降低了计算量。
关键词:交会对接仿真平台;视觉系统;惯性系统;截断奇异值UKF;信息融合
中图分类号:V448.2 文献标志码:A 文章编号:1672-7207(2011)S1-0458-06
Position and attitude determination with vision and inertial system
integration based on TSVD-UKF algorithm
SONG Shen-min, WEI Xi-qing
(Center of Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China )
Abstract: A truncated singular value decomposition UKF (TSVD-UKF) algorithm was presented to fuse measurements from vision system and IMU system for position and attitude determination of 4-DOF spacecraft docking simulator. To avoid the difficulty of calculating Jacobian and the divergence for the problem caused by linearization of EKF, UKF algorithm was employed which is more accurate and robust for position and attitude determination. Truncated singular value decomposition was adopted to generate smaller size of sigma points for UKF to reduce computational cost caused by large dimension of state. Experimental results validate accuracy and efficiency of the TSVD-UKF fusion algorithm.
Key words: air-bearing simulator of rendezvous and docking; vision system; inertia system; TSVD-UKF; information fusion
交会对接过程中要求2个航天器不能发生碰撞,这是至关重要的安全要求。因此对航天器的导航和控制精度提出了苛刻的要求,需要大量理论研究和物理仿真。利用气浮技术进行全物理仿真是发展较早并且被广泛采用的一种行之有效的手段[1]。“四自由度对接仿真平台”采用了单轴气浮轴承的形式,开发的对接与分离地面演示系统,用于仿真验证最后逼近阶段的制导与控制规律、反作用飞轮和气动系统进行卫星姿态控制以及位姿测量系统的有效性和可靠性。追踪星是通过其上安装的CCD相机对目标星上所安装的光学目标测量来实现位姿的确定,更新频率大约10 Hz。但由于视觉系统的CCD相机仅有40°左右的有限视野,因此一旦追踪星转动使目标超出视野,就会造成视觉位姿确定失败。IMU可以测量载体六自由度的线加速度和角速度的信息,且更新速率可以达到100 Hz,但是由于漂移存在,造成误差随时间累积越来越大。通过视觉系统与IMU结合的方法,可以使2种测量装置优势互补,在滤波的预测阶段使用IMU测量数据,量测更新使用视觉系统的数据,既提高了整个系统的更新频率和测量范围又改善了系统的测量精度。利用陀螺仪以及星敏感器等装置的扩展卡尔曼滤波(EKF)姿态确定算法在20世纪80年代初成为研究热点[2-3],并逐渐发展为一种成熟方法,成功应用于多种飞行器的导航上[4]。由于EKF通过对非线性系统一阶线性化求取均值和方差,存在近似误差大和求取Jacobian矩阵困难的问题。相比于EKF逼近一个非线性函数,Unscented卡尔曼滤波(UKF)方法[5-7]通过选取采样点集逼近高斯分布,显然具有更高的精度。但是采样点集的个数大约是系统状态维数的2倍,计算量随着系统维数而上升,当系统维数过大时并不实用。为了利用视觉摄像机获得的位姿信号及俯仰和偏航陀螺仪和加速度计输出信息来有效地确定仿真平台的位置和姿态,本文作者提出了一种通过截断奇异值分解来选取采样点集的方法的TSVD-UKF算法,并将其用于视觉和惯导融合位姿确定算法中。
1 运动学模型
1.1 姿态运动模型
修正的罗德里格参数[8]用无冗余的三维向量表示姿态,相比欧拉角具有的优势是在360°时才会出现奇异值。修正的罗德里格参数表示的姿态旋转矩阵:

其中: ,修正的罗德里格参数的合成运算具有如下形式:
,修正的罗德里格参数的合成运算具有如下形式:

如果将上式中的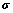 定义为原始修正罗德里格参数,
定义为原始修正罗德里格参数, 为增量修正罗德里格参数,则四元数
为增量修正罗德里格参数,则四元数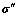 的含义是在
的含义是在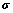 的基础上增加了
的基础上增加了 角度,其相应的姿态矩阵的形式:
角度,其相应的姿态矩阵的形式:

修正的罗德里格参数表示的姿态运动学方程:
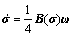
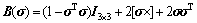
1.2 融合IMU的系统状态方程
IMU通过加速度计和陀螺仪实现对载体线加速度和角速度的实时测量,具有较高的采样频率,因此能够跟踪飞机和卫星等高速运动载体的动态特性。另外,IMU不依赖于外界的辅助,既不发射也不接收信号,具有完全自主的特性。然而IMU的测量值中包含测量噪声和漂移量,并且漂移随时间累积,不能单独长时间工作。IMU可以测量六自由度的载体信息,3个自由度加速度和3个自由度角速度的系统模型为:

其中: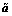 是加速度计测量值沿体轴的输出;a是真实的加速度;ba是加速度计漂移;
是加速度计测量值沿体轴的输出;a是真实的加速度;ba是加速度计漂移;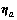 是加速度计测量白噪声;
是加速度计测量白噪声;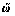 是陀螺仪绕体轴旋转的角速度;
是陀螺仪绕体轴旋转的角速度; 是真实的角速度;
是真实的角速度; 是陀螺仪漂移;
是陀螺仪漂移;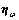 是陀螺仪测量白噪声。
是陀螺仪测量白噪声。
应用EKF滤波方法需要精确已知系统的状态方程,从而预测系统的状态。然而,由于实际载体运动较为复杂,很难准确建立系统的运动学模型。在本系统中由于存在高精度IMU,能够以较高采样频率提供载体精确的线加速度和角速度信息,因此本文建立包含IMU线加速度和角速度测量值的状态方程:
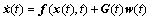
其中:状态向量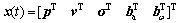 是15维的列向量,p和v分别表示位置和速度。式具体写为:
是15维的列向量,p和v分别表示位置和速度。式具体写为:

其中:AB/N表示从导航系到体系的坐标转换矩阵;因此,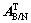 表示从体系到导航系的坐标转换矩阵;va和
表示从体系到导航系的坐标转换矩阵;va和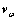 分别为加速度计和陀螺仪的一阶马尔科夫过程白噪声。
分别为加速度计和陀螺仪的一阶马尔科夫过程白噪声。
视觉系统可以测量载体相对于目标星的六自由度的相对位置和姿态信息:
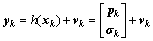
其中:vk表示零均值的量测白噪声。由于本文中实际实验平台的目标星是一个固定目标,因此本系统将导航系定义在目标星上,所以可以进行视觉和IMU两者的测量信息融合。
2 基于EKF的视觉/惯性融合算法
由系统的状态方程(8),可得其Jacobian矩阵:

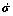 对
对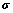 的偏导数:
的偏导数:
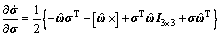
状态方程的噪声向量w也是一个15维列向量:

系统相应的噪声驱动矩阵:

3 基于TSVD-UKF的视觉/惯性融合算法
3.1 UKF的视觉/惯性融合算法
EKF方法自提出以来在非线性估计问题得到了广泛的应用,但是EKF方法推导Jacobian矩阵比较困难且有时难以实现。另外,EKF方法对非线性系统进行一阶近似,对变换后的高斯随机变量(Gaussian Random Variable,GRV)后验均值和方差引入较大误差,使得估计为次优估计,甚至可能造成滤波器发散。为克服上述问题,Julier等提出了UKF算法用于非线性系统估计。UKF算法是由一些采样点的集合,通过非线性变换(UT变换)的点来逼近GRV的均值和方差。经过证明,这种逼近对任意非线性函数泰勒展开精确达到二阶,而EKF精确只能达到一阶[9]。
视觉与IMU位姿确定系统具有很强的非线性,且状态初值估计误差较大,使用UKF可以提供更好的估计精度。其UKF的融合算法与普通UKF类似[10],具有如下形式:
对于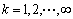 :
:
首先计算(2n+1)个采样点集(Sigma点集):

时间更新:

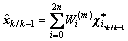


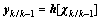
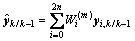
量测更新:


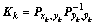
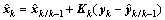
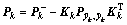
其中: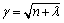 ;λ是调整尺度参数;n是状态的维数,Rv是过程噪声方差阵;Rn是量测噪声方差阵。相应权值Wi可取为:
;λ是调整尺度参数;n是状态的维数,Rv是过程噪声方差阵;Rn是量测噪声方差阵。相应权值Wi可取为:
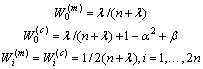
3.2 TSVD-UKF算法
需要注意的是,UKF中采样点的个数约为系统状态维数的2倍,因此当系统维数较大时计算量也随之增大。为了解决这个问题,提出了采用截断奇异值分解[11]选取采样点,在保证估计精度的前提下,采取舍弃一些次要采样点的方法来减少计算量。为选取采样点首先对后验协方差矩阵Pk进行奇异值分解:

其中: 是由Pk的特征值构成的对角阵,并按照降序进行排列,即当i>j时
是由Pk的特征值构成的对角阵,并按照降序进行排列,即当i>j时 ,
, 是由相应的特征向量组成的矩阵。通过选取前lk个特征值和特征向量的乘积
是由相应的特征向量组成的矩阵。通过选取前lk个特征值和特征向量的乘积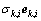 ,来构成2lk+1个新的采样点集:
,来构成2lk+1个新的采样点集:
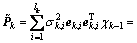

通过截断的奇异值分解,后验协方差矩阵Pk近似为:
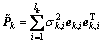
从而保证了协方差矩阵的正定性。
lk决定了改进UKF的性能,取值过小会造成Pk中的重要信息丢失;当lk取值过大时, 相对于主要特征值可以忽略不计,增加lk对于精度没有明显提升却造成不必要的计算量增加。因此需要折中选取lk来同时保证UKF的精度和效率。
相对于主要特征值可以忽略不计,增加lk对于精度没有明显提升却造成不必要的计算量增加。因此需要折中选取lk来同时保证UKF的精度和效率。
本文提出了一种在每个滤波周期中自适应调整lk的方法,取lk为整数且满足:

其中:hk是第k个滤波周期的阈值。为了避免lk过大或者过小,通过调整hk来保证lk位于[ll lu]中。在滤波开始时如果hk恰好满足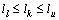 ,则在下一个滤波周期保持hk不变。如果通过hk确定的lk小于下限值,重置hk为
,则在下一个滤波周期保持hk不变。如果通过hk确定的lk小于下限值,重置hk为 ;反之,如果hk过大导致
;反之,如果hk过大导致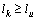 ,则重置hk为
,则重置hk为 。重复上述操作,直到lk进入指定的范围。在下一个滤波周期令
。重复上述操作,直到lk进入指定的范围。在下一个滤波周期令 ,然后重复以上过程使
,然后重复以上过程使 在上下限区间之内。
在上下限区间之内。
通过以上步骤,就实现了自适应折中选取lk值来动态调整选取采样点集的大小。从而改进的UKF算法在保证估计精度的同时,减少了所需的计算量。
4 实验结果
这部分通过四自由度对接仿真平台实验来验证本文所提出的基于改进的UKF确定位姿算法的有效性。实验采用的IMU的更新频率为100 Hz,加速度计测量噪声标准差和漂移标准差分别为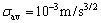 和
和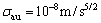 ,陀螺仪测量噪声标准差和漂移噪声标准差分别为
,陀螺仪测量噪声标准差和漂移噪声标准差分别为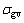 =10-3 (°)/s1/2和
=10-3 (°)/s1/2和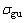 = 10-8 (°)/s3/2。而视觉采样频率为10 Hz,采用的CCD相机由于CCD固有的A/D转换精度和光线变化以及杂散光对成像质量影响等原因带来的噪声影响,位置和角度的测量分别具有σpos=2 cm和σatt=0.5°标准差的噪声影响。滤波器开始工作时,初始位置估计值为20 cm,初始角度估计为1°,初始速度、加速度计和陀螺漂移的估计值均设为0。
= 10-8 (°)/s3/2。而视觉采样频率为10 Hz,采用的CCD相机由于CCD固有的A/D转换精度和光线变化以及杂散光对成像质量影响等原因带来的噪声影响,位置和角度的测量分别具有σpos=2 cm和σatt=0.5°标准差的噪声影响。滤波器开始工作时,初始位置估计值为20 cm,初始角度估计为1°,初始速度、加速度计和陀螺漂移的估计值均设为0。
EKF,UKF和TSVD-UKF 3种滤波算法在四自由度对接仿真平台上进行了对比实验。图1所示为位置估计信号误差曲线。可见:利用视觉测量的位置信号与IMU加速度进行信息融合后,EKF滤波精度略有提高;而2种UKF算法位置估计误差小于0.5 cm,精度较单独使用视觉系统明显提高。图2所示为角度的误差曲线。可见,3种滤波器的估计精度都很高,角度误差都小于0.05°,其中EKF估计误差略低于其他2种滤波器的估计误差。图3和图4所示分别是加速度计和陀螺仪的漂移估计误差。也可以看出:2种UKF收敛速度较快,且稳态误差小于EKF。可见:无论是EKF,UKF还是TSVD-UKF,位姿和漂移的估计都快速收敛,这是由于视觉测量同时含有位置和角度数据,能够用于滤波校正。由于系统维数15维,其UKF算法采样点个达到31,而TSVD-UKF在运行中lk平均值小于8,采样点个数大幅下降,因此节约了大量的计算量。而从实验结果可以看出,提出的TSVD-UKF与UKF估计精度相当,滤波器收敛速度略低于UKF。
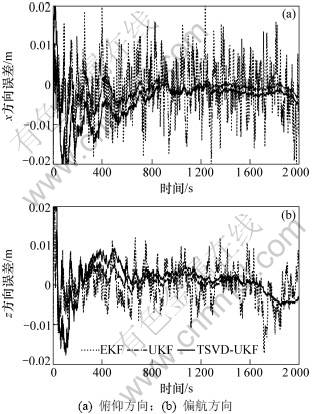
图1 位置估计误差
Fig.1 Estimation errors of position
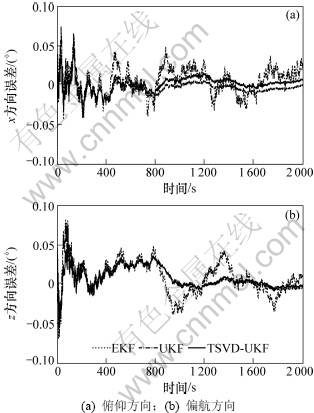
图2 角度估计误差
Fig.2 Estimation errors of attitude

图3 加速度计漂移估计误差
Fig.3 Estimation errors of accelerometers bias

图4 陀螺仪漂移估计误差
Fig.4 Estimation errors of gyros bias
5 总结
针对四自由度对接仿真系统运动复杂的特性,充分利用了IMU加速度和角速度更新速度快的特性,建立了基于IMU输出的系统运动学模型。为克服了视觉系统采样频率低和IMU测量值漂移随时间累积的问题,采用了EKF对视觉和IMU进行数据融合。由于EKF应用在此类非线性问题存在Jacobian矩阵求解困难以及线性化容易造成滤波发散的不足,提出了利用UKF融合视觉测量和IMU数据进行位姿确定算法来提高位姿计算精度。为解决UKF随系统状态维数计算量过大的问题,提出一种利用自适应截断奇异值分解来选取采样点集的TSVD-UKF算法,既保证了新算法具有与普通UKF相似的精度同时在解决高维系统滤波问题时具有计算量小、易于实现的优点。
参考文献:
[1] Schwartz J, Peck M, Hall C. Historical review of air-bearing spacecraft simulators[J]. Journal of Guidance Control and Dynamics, 2003, 26(4): 513-522.
[2] Lefferts E J, Markley F L, Shuster M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(5): 417-429.
[3] Murrell J. Precision attitude determination for multimission spacecraft[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Palo, CA, 1978: 70-87.
[4] Andrews S F and Bilanow S. Recent flight results of the TRMM Kalman filter[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Monterey, CA, 2002: 1-10.
[5] Julier S J, Uhlmann J K, Durrant-Whyte H F. New approach for filtering nonlinear systems[C]//Proceedings of the American Control Conference. Seattle, WA, 1995: 1628-1632.
[6] Julier S J and Uhlmann J K. A new extension of the kalman filter to nonlinear systems[C]//Proceedings of the SPIE, Volume 3068, Signal Processing, Sensor Fusion, and Target Recognition VI. Orlando, Florida, 1997: 182-193.
[7] van Der Merwe R, Wan E A. The square-root unscented Kalman filter for state and parameter estimation[C]//Proceedings of 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Salt Lake, 2001: 3461-3464.
[8] Crassidis J L, Markley F L. Attitude estimation using modified Rodrigues parameters[C]//Proceedings of the American Astronautical Society F. Landis Markley Astronautics Symposium, Greenbelt, MD, 1996: 71-86.
[9] Wan E A, van der Merwe R. The unscented Kalman Filter for nonlinear estimation[M]. Alberta: Lake Louise, 2000: 229-234.
[10] Crassidis J L. Sigma-point Kalman filtering for integrated GPS and inertial navigation[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference. San Francisco, CA, 2005: 1981-2004.
[11] Hansen P C, Sekii T, Shibahashi H. The modified truncated SVD method for regularization in general form[J]. SIAM Journal on Scientific and Statistical Computing, 1992, 13(5): 1142-1150.
(编辑 赵俊)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家高技术研究发展计划(“863”计划)项目(2010AA7045003)
通信作者:魏喜庆(1982-),男,黑龙江鹤岗人,博士研究生,从事编队飞行等研究;电话:15124504182;E-mail: weixiqing@gmail.com