Trans. Nonferrous Met. Soc. China 22(2012) s673-s677
Grain size dependence of flow stress in ECAPed Ti with constant texture
Chang-Young HYUN1, Ho-Kyung KIM2
1. Department of Materials Science and Engineering, Seoul National University of Science and Technology, 172 Kongneung-dong, Nowon-ku, Seoul 139-743, Korea;
2. Department of Automotive Engineering, Seoul National University of Science and Technology, 172 Kongneung-dong, Nowon-ku, Seoul 139-743, Korea
Received 21 May 2012; accepted 22 September 2012
Abstract: The effect of grain size on the flow stress in an ECAPed Ti with a constant texture was investigated, assuming that 2, 4, 5 and 6 passes microstructures have a similar texture. The average size of recrystallized grains decreased to 0.5 μm, 0.4 μm, and 0.3 μm with respect to the ECAP pass number of 2, 4, and 6, respectively. The ultimate tensile strength (UTS) and yield strength (YS) increase with an increase in the number of pressing. The UTS and YS of the 6 passes ECAPed sample were found to be 740.2 MPa and 580.3 MPa, respectively. An equation for the flow stress of an ECAPed Ti with a constant texture as a function of the strain and grain size was derived for the ECAPed metal. The following equation was finally obtained: σ(ε)=103.9+1825ε-9.6ε1/2·d-1/2+8.3d-1/2.
Key words: Ti; mechanical properties; grain size; flow stress; equal channel angular pressing
1 Introduction
Equal channel angular pressing (ECAP) is an effective method that produces a relatively large volume of bulk material with ultra-fine grains [1-4]. The ECAP process has been proven very effective in enhancing the strength of aluminum [5,6], steel [7,8], nickel [9], titanium [10] and copper [11,12]. Texture modification has also been reported to occur in aluminum alloys during the ECAP process [2]. However, the effect that texture has on the strength of an alloy is not significant compared to the effect of the grain refinement on strength, as the standard Hall-Petch relationship (a positive slope in the plot of yield stress vs. grain size d-1/2) is valid even after ECAP [2] as aluminum with a FCC structure has abundant slip systems. In contrast, the effect of texture on strength may prevail over the effect of grain refinement on the strength in metals or alloys with a HCP structure, as these alloys poses limited number of slip systems. In this work, the effect of the grain size on the flow stress in an ECAPed Ti with a constant texture was investigated. An equation for the flow stress of this alloy with a constant texture as a function of the strain and grain size was derived from experimental results. In addition, the contribution of texture after extrusion to the flow stress is quantified.
2 Experimental
A commercially pure titanium (grade 2) was cut to the rods with diameter of 14.5 mm and length of 90 mm and then annealed at 1073 K for 1 h in Ar atmosphere, and then quenched into room-temperature water. Its chemical composition was Ti-0.06Fe-0.01N-0.01O- 0.01H (mass fraction, %). The average grain size was 105 μm after the heat treatment. ECAP was conducted using a die with an internal angle Φ of 110° and an outer curvature angle Ψ of 25°. The present ECAP die was designed to give an approximate strain e of about 0.76 on each pressing.
Repetitive pressings of the same sample were performed to 6 passes. During ECAP, all pressings were conducted at 683 K, using the procedure designated as route Bc, in which each sample was rotated 90° around its longitudinal axis between the passages. Tensile properties in longitudinal directions of the ECAPed and unECAPed Ti rods were measured using the miniature tensile specimens with geometry of 3 mm gauge length, 1 mm gage width, 1 mm thickness, and 2 mm shoulder radius. The tensile samples were extracted from the center portion of the ECAPed and unECAPed rods in longitudinal direction using electro-discharge machining, as shown in Fig. 1. A displacement rate of 1 mm/min was used for tensile testing, corresponding to an initial strain rate of 3.3×10-3 s-1. The CCD camera as an extensometer was adopted during tensile test.

Fig. 1 Tensile sample extracted from ECAPed rod
3 Results and discussion
After 2 passes of ECAP, the observed slip band width was thinner than that of the first pass, and the band interfaces were distinguished more clearly (Fig. 2(a)). Meanwhile, the straight-shaped bands varied partially to the crooked shape in the severely strained region. Moreover, the discriminable images with average size of about 0.5 μm were also observed in the intermittent places of the broken slip bands, indicating the most severely strained region. These images represented the clusters of low angle grain boundaries as mentioned above. When 6 passes were finished, the recrystallized grains were observed as similar as that of the rod after 4 passes (Fig. 2(b)). However, the size distribution of the grains was more uniform than that of the fourth pass. The accumulated deformation energy by the additional ECAP process might change the sub-micron grains into the finer ones. However, significant grain size reduction was not observed and the average size of the recrystallized grains was approximately 0.3 μm. In summary, the average size of recrystallized grains decreased to 0.5, 0.4 and 0.3 μm with respect to the ECAP pass number of 2, 4, and 6, respectively.

Fig. 2 TEM micrographs of pure Ti observed after ECAP
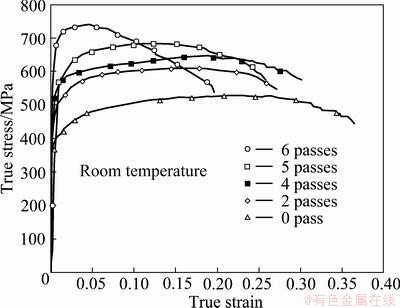
Fig. 3 Stress against true strain curves of unECAPed and ECAPed Ti
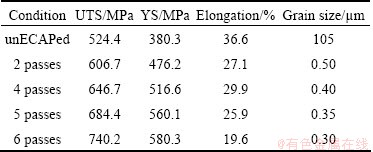
The true stress—strain curves of the unECAPed, 2, 4, 5, and 6 pass ECAPed Ti samples are shown in Fig. 3. Their data for yield stress (YS), ultimate tensile strength (UTS), elongation to failure and grain size are summarized in Table 1. The UTS and YS increase with an increase in the number of pressings. The ultimate tensile strength (UTS) and yield strength (YS) of the 6 passes ECAPed sample were found to be 740.2 MPa and 580.3 MPa, respectively. In contrast, the UTS and YS of the unECAPed sample were 524.4 MPa and 380.3 MPa, respectively. As similar to the tensile behavior of UFG materials reported previously [1], the ECAPed sample showed a little strain hardening. After 6 passes ECAP, the ultimate tensile strength was increased by 41%. This is most likely due to considerable grain refinement through severe deformation by ECAP. This fact suggests that the UFG structure of pure Ti is very advantageous for improving titanium’s strength without alloying, so that it would be suitable for use in medical devices. The tensile elongation was, however, largely decreased by 46% from unECAPed to 6 passes. This is related to the decrease of strain hardening capability after ECAP, which commonly occurs in other alloys after ECAP [1].
Table 1 Average grain size and room temperature mechanical properties of unECAPed and ECAPed Ti
In Fig. 4, a 0.2% yield stress is plotted against d-1/2 for the unECAPed and ECAPed Ti, showing the unECAPed has different slope from the ECAPed Ti. The change of the slope in YS observed in the results can be attributed to different texture during repeated ECAP processing of the Ti. A standard Hall-Petch relationship (positive slope) was observed in the 2 to 6 passes ECAPed samples, suggesting that the texture remains unchanged after the 2 passes ECAP process. Thus, it is worthwhile to quantify the effect of the grain size on the flow stress in the ECAPed Ti by excluding the effect of texture, assuming that the 2, 4, 5, and 6 passes microstructures have the same texture.
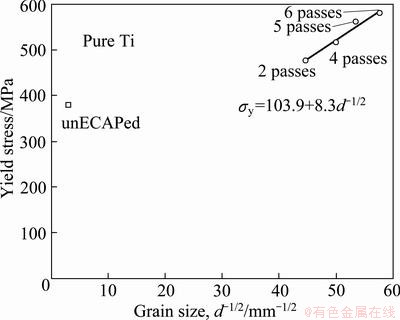
Fig. 4 0.2% yield stress against d-1/2 for unECAPed and ECAPed Ti
The Hall-Petch relationship correlates the grain size of a material to its yield stress. According the to Hall-Petch relationship, the yield stress σy of a material can be expressed as
σy=σoy+kyd-1/2 (1)
where σoy is the friction stress, ky is the stress intensity for plastic yielding across polycrystalline grain boundaries, and d is the grain size in mm. ARMSTRONG et al [13] modified the Hall–Petch relationship and proposed that the flow stress of a material is related to the grain size according to the equation
σ(ε)=σo(ε)+k(ε)·d-1/2 (2)
where σ(ε) is the flow stress at a particular strain, σo(ε) is a component of the flow stress that is independent of the grain size, and k(ε) is a constant at a particular strain representing the intensity of the strengthening of the grain size. PHILLIPS and ARMSTRONG [14] proposed the following equation for the flow stress of a material.
σ(ε)=σoy+Aε+Bε1/2·d-1/2+ky·d-1/2 (3)
The values of σoy and ky were determined to be 103.9 MPa and 8.3 N/mm3/2, respectively, from Fig. 4. The grain size dependence of ky in the present samples (=8.3 MPa·mm1/2) is much lower than that for pure Ti (=21.2 MPa·mm1/2) [15]. At present it is not clear why there is difference. This may be due to a difference in the impurity content in Ti.
A plot of the flow stresses of the 2, 4, 5, and 6 passes samples against the grain size (d-1/2) for strains ranging from 1% to 4% is shown in Fig. 5. The dependence of the flow stress on the grain size for all of the investigated strains suggests that the modified Hall-Petch relationship (Eq. (2)) is valid for the 2, 4, 5, and 6 passes ECAPed Ti. The values of σo(ε) and k(ε) for strains ranging from 1% to 4% are determined and summarized in Table 2. From Table 2, it can be seen that the value of the lattice friction stress σo(ε) for the Ti increases as the strain increases due to the stain hardening within the grain volumes. It is also apparent from Table 2 that k(ε) decreases as the strain in the range of 1%-4% strain increases.
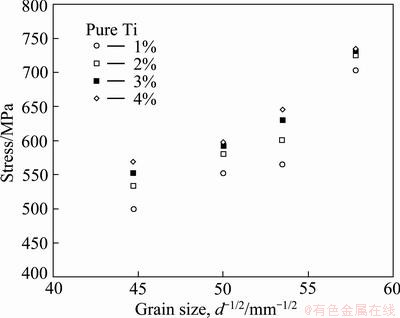
Fig. 5 Flow stress against d-1/2 of 2, 4, 5 and 6 passes ECAPed Ti for strains ranging from 1% to 4%
Table 2 Hall-Petch constants σo(ε) and k(ε) for 2, 4, 5 and 6 passes ECAPed Ti
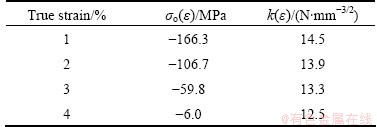
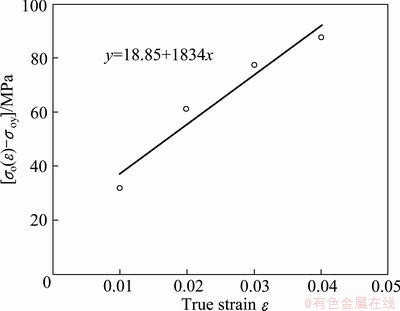
Fig. 6 Variation of [σo(ε)-σoy] with true strain for 2, 4, 5 and 6 passes ECAPed Ti
Figure 6 shows the variation of [σo(ε)-σoy] with the true strain ε for the ECAPed Ti. It is shown from Fig. 6 that [σo(ε)-σoy] increases linearly with the true strain. The following relationship was obtained from Fig. 6:
σ(ε)=σoy+A·ε=103.9+1834ε (4)
The variation of [k(ε)-ky] with ε1/2 is shown in Fig. 7. The value of [k(ε)-ky] increases linearly with ε1/2. The following relationship was derived from Fig. 7:
k(ε)=ky+B·ε1/2=8.3-19.6ε1/2 (5)
Substituting Eq. (4) and (5) into Eq. (2) gives
σ(ε)=σoy+Aε+Bε1/2·d-1/2+ky·d-1/2 (6)
Substituting the numerical values for σoy, ky, A, and B, the following equation is finally obtained:
σ(ε)=103.9+1834ε-19.6ε1/2·d-1/2+8.3d-1/2 (7)
It is necessary to verify the above equation for the 2, 4, 5, and 6 passes ECAPed Ti. Figure 8(a) shows the experimental and predicted flow stress values plotted against the strain for the 2 passes ECAPed Ti. The experimental flow stress values are in good agreement with those from the predicted values according to Eq. (7). A comparison between the prediction of Eq. (7), which considers only the effect of the grain size on the flow stress, and the experimental results, which includes the effects of texture and grain size was made in an effort to isolate the effect of texture on the flow stress. This is plotted in Fig. 8(b). From Fig. 8(b), it can be seen that the contribution of texture in the unECAPed sample was determined to be 251 MPa from the value of 449 MPa of the experimental result and that of 198 MPa predicted by Eq. (7), assuming the grain size is 105 μm with a similar texture to the 2, 4, 5 and 6 passes ECAPed samples. The value of 251 MPa may be the corresponding contribution of texture resulting from the extrusion process. This demonstrates how important the effect of texture modification is on the strength of Ti.
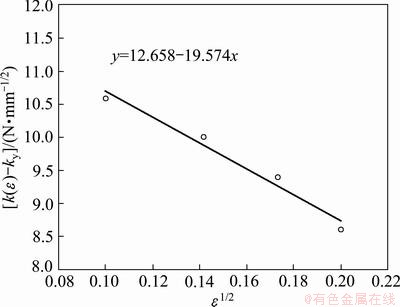
Fig. 7 Variation of k(ε)-ky with ε1/2 for 2, 4, 5 and 6 passes ECAPed Ti
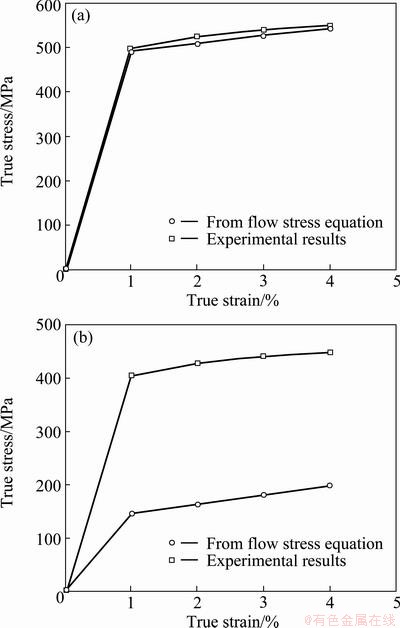
Fig. 8 Experimental and predicted flow stress values plotted against strain for 2 passes ECAPed (a) and unECAPed Ti (b)
4 Conclusions
The effect of grain size on the flow stress in an ECAPed Ti with a constant texture was investigated, assuming that 2, 4, 5 and 6 passes microstructures have a similar texture. The ultimate tensile strength (UTS) and yield strength (YS) increase with an increase in the number of pressings. The UTS and YS of the 6 passes ECAPed sample were found to be 740.2 MPa and 580.3 MPa, respectively. In contrast, the UTS and YS of the unECAPed sample were 524.4 MPa and 380.3 MPa, respectively. The Hall-Petch constants of the ECAPed Ti with a constant texture are related to the true strain in such a way that σo(ε) is proportional to ε and k(ε) having a negative slop with ε1/2. An equation of the flow stress, σ(ε)=103.9+1834ε-19.6ε1/2·d-1/2+8.3d-1/2, is derived for 2, 4, 5 and 6 passes ECAPed Ti with a constant texture.
References
[1] FURUKAWA M, IWAHASHI Y, HORITA Z, NEMOTO M, TSENEV N, VALIEV R Z, LANGDON T G. Structural evolution and the Hall-Petch relationship in an Al-Mg-Li-Zr alloy with ultra-fine grain size [J]. Acta Materialia, 1997, 45: 4751-4757.
[2] IWAHASHI Y, FURUKAWA M, HORITA Z, NEMOTO M, LANGDON T G. Microstructural characteristics of ultrafine-grained aluminum produced using equal-channel angular pressing [J]. Metallurgical and Materials Transaction A, 1998, 29: 2245-2252.
[3] HOSSEINI E, KAZEMINEZHAD M. The effect of ECAP die shape on nano-structure of materials [J]. Computational Materials Science, 2009, 44: 962-967.
[4] HOSEINIA M, MERATIAN M, TOROGHINEJAD M, SZPUNAR J. Texture contribution in grain refinement effectiveness of different routes during ECAP [J]. Materials Science and Engineering A, 2008, 497: 87-92.
[5] WANG J, DUAN Q, HUANG C, WU S, ZHANG Z. Tensile and compressive deformation behaviors of commercially pure Al processed by equal-channel angular pressing with different dies [J]. Materials Science and Engineering A, 2008, 496: 409-416.
[6] GUTIERREZ-URRUTIA I, MUNOZ-MORRIS M, MORRIS D. Contribution of microstructural parameters to strengthening in an ultrafine-grained Al–7%Si alloy processed by severe deformation [J]. Acta Materialia, 2007, 55: 1319-1330.
[7] PARK K T, KIM Y S, LEE J G, SHIN D H. Thermal stability and mechanical properties of ultrafine grained low carbon steel [J]. Materials Science and Engineering A, 2000, 293: 165-172.
[8] SHIN D, PARK P, Ultrafine grained steels processed by equal channel angular pressing [J]. Materials Science and Engineering A, 2005, 410-411: 299-302.
[9] KRASILNIKOV N, LOJKOWSKI W, PAKIELA Z, VALIEV R. Tensile strength and ductility of ultra-fine-grained nickel processed by severe plastic deformation [J]. Materials Science and Engineering A, 2005, 397: 330-337.
[10] KIM W, HYUN C, KIM H. Fatigue strength of ultrafine-grained pure Ti after severe plastic deformation [J]. Scripta Materialia, 2006, 54: 1745-1750.
[11] VINOGRADOV V, PATLAN V, SUZUKI Y, KITAGAWA K, KOPYLOV V. Structure and properties of ultra-fine grain Cu-Cr-Zr alloy produced by equal-channel angular pressing [J]. Acta Materialia, 2002, 50: 1639-1651.
[12] IWAHASHI Y, WANG J, HORITA Z, NEMOTO M, LANGDON T G. Principle of equal-channel angular pressing for the processing of ultra-fine materials [J]. Scripta Materialia, 1996, 35: 143-146.
[13] AMSTRONG R, CODD I, DOUTHWAITE R M, PETCH N J. The plastic deformation of polycrystalline aggregates [J] Philosophical Magazine, 1962, 7: 45-58.
[14] PHILLIPS W L, ARMSTRONG R W. The strain dependence of the flow stress—grain size relation for 70-30 brass [J]. Metallurgical Transaction A, 1972, 3: 2571-2577.
[15] SALEM A A, KALIDINDI S R, DOHERTY R D. Strain hardening regimes and microstructure evolution during large strain compression of high purity titanium [J]. Scripta Materialia, 2002, 46: 419-423.
(Edited by YANG You-ping)
Corresponding author: Ho-Kyung KIM; Tel: +82-2-9706348; E-mail: kimhk@snut.ac.kr
DOI: 10.1016/S1003-6326(12)61784-1