Trans. Nonferrous Met. Soc. China 23(2013) 3722-3728
Effect of liquid diffusion coefficients on microstructure evolution during solidification of Al356.1 alloy
Wei-hua SUN1,2, Li-jun ZHANG1,2, Ming WEI1,2, Yong DU1,2, Bai-yun HUANG1
1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;
2. Sino-German Cooperation Group “Microstructure in Al alloys”, Central South University, Changsha 410083, China
Received 20 July 2013; accepted 25 October 2013
Abstract: The effect of liquid diffusion coefficients on the microstructure evolution during solidification of primary (Al) phase in Al356.1 alloy was investigated by means of the phase-field simulation using two sets of diffusion coefficients in liquid phase, while fixing other thermophysical and numerical parameters. The first set is only with impurity coefficients of liquid phase in Arrhenius formula representing only the temperature dependence. While the second set is with the well-established atomic mobility database representing both temperature and concentration dependence. For the second set of liquid diffusion coefficients, the effect of non-diagonal diffusion coefficients on the microstructure evolution in Al356.1 alloy during solidification was also analyzed. The differences were observed in the morphology, tip velocity and composition profile ahead of the tip of the dendrite due to the three cases of liquid diffusivities. The simulation results indicate that accurate databases of mobilities in the liquid phase are highly needed for the quantitative simulation of microstructural evolution during solidification.
Key words: Al356.1 alloy; solidification; microstructure evolution; diffusion coefficient; phase-field simulation
1 Introduction
Quantitative description of microstructure evolution during solidification is the prerequisite for the novel materials design. Over the past decades, important advances have been made in this field, especially as the mature of a variety of powerful computational simulation techniques. The phase-field simulation, one of such powerful simulation techniques, has become a very effective tool for simulation of microstructure evolution of materials over the past two decades [1-5]. The key for quantitative phase-field simulation is the input of reasonable thermophysical parameters, for instance, the temperature- and concentration-dependent chemical driving force and diffusivities, which can be naturally retrieved from the thermodynamic and atomic mobility databases established via the CALPHAD (calculation of phase diagram) method [6-9]. Nowadays, most of the phase-field simulations coupling with the CALPHAD thermodynamic and atomic mobility databases have been devoted to binary or ternary alloys [10]. However, such reports are very scarce for multicomponent alloys, which instead are actual materials in real world [11]. As the number of solute component increases, the interaction between different solutes becomes extremely complicated, resulting in the complex nature in description of microstructure evolution in multicomponent alloys. Taking the solidification in multicomponent alloys for example, the diffusion flux of one component depends not only on its own composition gradient, but also on the composition gradients of other components. In order to accurately describe the diffusion process in multicomponent alloy during solidification, the reasonable composition- and temperature-dependent full diffusivity matrices in the target alloy are needed.
Up to now, thermodynamic databases for most commercial multicomponent alloys have been constructed, such as steel, Ni-based superalloys, Al-based alloys, Mg-based alloys [12]. As for atomic mobility databases, they are also available for some multicomponent alloys [12], but mainly limited to solid solution phases, like FCC, BCC, etc. While for the liquid phase, which is the most important phase during solidification, its atomic mobility database is usually missing except for Al-based alloys [13]. The major obstacle associated with the establishment of atomic mobility database in liquid phase is lack of the reliable liquid diffusivity data due to the experimental difficulties caused by convection in melts. Therefore, either a constant diffusivity (i.e, 1×10-9 m2/s) [14] or diffusivity in Arrhenius equation representing only the temperature dependence [15] is commonly used in various diffusion simulations. These simplifications may lead to great uncertainties in the solidification simulations because the diffusivities in liquid are usually dependent on both temperature and composition.
Consequently, before the quantitative phase-field simulation of the solidified microstructure, it is necessary to investigate the effect of different liquid diffusion coefficients on the microstructure evolution in multicomponent alloys as the major aim in the present work. There exist several previous investigations on the effect of liquid diffusivities. They focus on either binary alloys [14] or ternary alloys during isothermal solidification [16]. In the present work, a commercial multicomponent alloy, Al356.1 (Al-0.46Fe-0.3Mg- 0.32Mn-6.97Si; mass fraction, %), is chosen as the target alloy. Very recently, the thermodynamic database, as well as the atomic mobility database for both liquid and solid solution phases, in the Al-Cu-Fe-Mg- Mn-Ni-Si-Zn system, has been established in our research group [13,17]. In order to achieve the major aim in the present work, two-dimensional (2-D) phase-field simulations of the evolution of primary (Al) phase in Al356.1 alloy during solidification with a cooling rate of 2 K/s are to be performed by means of MICRESS (microstructure evolution simulation software) [18] using two sets of diffusion coefficients. The first set is only with impurity coefficients of liquid phase in Arrhenius form from DU et al [15], named as “Case 1”. While the second set is the well-established atomic mobility database for liquid phase [19]. In order to further study the effect of non-diagonal diffusion coefficients on microstructure evolution, the second set of diffusivities is divided into two cases: one is only with diagonal terms (named as “Case 2”) and the other is with both diagonal and non-diagonal terms (named as “Case 3”).
2 Phase-field model
We start from a general free energy, F, consisting of the interfacial energy density, fintf, and the chemical energy density, fchem, which is expressed as follows [4,20]:
 (1)
(1)
 (2)
(2)
 (3)
(3)
where N is the local number of phases; φα is the phase field of an α phase/grain, which should always fulfill the sum constraint:
 (4)
(4)
σαβ is the interfacial energy between the phases/grains α and β; ηαβ is the interfacial thickness, which is assumed to be equal for all the interfaces; h(φα) is a monotonic coupling function;  is the bulk free energy density of the individual phase;
is the bulk free energy density of the individual phase;  is the diffusion potential of component i introduced as a Lagrange multiplier to conserve the mass balance between the phases:
is the diffusion potential of component i introduced as a Lagrange multiplier to conserve the mass balance between the phases:
 (5)
(5)
The evolution equations for the phase field and the concentration can be derived from the variation principle with respect to the above free energy function [20]:

 (6)
(6)
 (7)
(7)
where μαβ is the interfacial mobility;  is the driving force
is the driving force
 (8)
(8)
from thermodynamic database via the TQ interface [12], which is incorporated in MICRESS [18] based on the so-called multi-phase-field (MPF) method [4]; Dα is the diffusion coefficient in phase α and can be either measured from the experiments or directly obtained from the CALPHAD atomic mobility database.
In order to simulate the dendrite structure of primary (Al) phase using the phase-field method, the anisotropy of the interfacial energy and the interface mobility should be taken into account. The interfacial energy between (Al) phase in cubic structure and liquid phase is expressed as follows [4]:
σ*(θ)=σ0[1-ε*cos(4θ)] (9)
where σ*(θ) is the effective interfacial energy; σ0 is the average interfacial energy; ε* is the effective anisotropy coefficient; θ is the angle between the normal direction of the interface and the direction of the x axis, and is expressed as
θ=arctan(φy/φx) (10)
where φy is the derivative of phase field φ with respect to y, while φx is the derivative of phase field φ with respect to x. When ε*=0, one has σ*(θ)=σ0, which means isotropy. When ε*=1, the anisotropy is the maximum. However, when θ=nπ/2 (n is the integer), σ*(θ)=0, which is impossible in real situation. Thus, the range of ε* is 0≤ε*<1. Actually, analogous expressions for anisotropy of interface mobility can be derived.
3 Simulation, results and discussion
3.1 Simulation setup
A 2-D domain with 400×400 grids (grid spacing: 0.5 μm) is employed for simulation in the present work. The interface width is set to be 2.5 μm. Initially, one (Al) grain with zero radius is set in the center of the domain, and the initial liquid composition is set to be exactly the composition of the target Al356.1 alloy, i.e., Al-0.46Fe- 0.3Mg-0.32Mn-6.97Si (mass fraction, %). The initial temperature is 887 K, which is just below the melting point of Al356.1 alloy. The cooling rate is 2 K/s.
The physical parameters are carefully chosen from the reasonable experiments or via some semi-empirical equations to reproduce the basically experimental characterization [21]. The interfacial energy and its anisotropy are set to be 169 mJ/m2 [22] and 0.2535 [23], respectively. The interface mobility is calibrated to be 3×10-2 cm4/(J·s) to guarantee the diffusion-controlled process according to Ref. [4]. The anisotropy of interface mobility is determined to be 0.3.
The thermodynamic descriptions of liquid and (Al) phases employed in the present phase-field simulation are directly taken from the Al database established in our research group [17]. The diffusivities in solid (Al) phase are also taken from the atomic mobility database from our research group [13]. As for the liquid diffusivities, two sets of data are utilized in the present work, as stated in Section 1. The first set is only with the impurity diffusivities of Fe, Mg, Mn and Si in liquid phase from DU et al [15], which are expressed in Arrhenius type:
D=D0exp[-Q/(RT)] (11)
where D0 is the frequency factor and Q is the activation energy. Their detail values are listed in Table 1. The phase-field simulation with this set of diffusivities is referred as “Case 1”.
Table 1 Impurity diffusivities of elements in liquid Al used for “Case 1” [15]

The second set is with the atomic mobility database recently established in our research group [19]. From atomic mobility, the diffusion coefficients depending on temperature and concentration can be calculated by
 (12)
(12)
where Mk is the atomic mobility; δki is the Kronecker delta (δki=1 if k=i, otherwise δki=0); μk is the chemical potential of component k. Based on Eq. (12), it is known that the diffusion coefficient matrix consists of two parts. One is the diagonal term, while the other is the cross term.
In order to analyze the effect of liquid diffusion coefficients on microstructure evolution, three cases of diffusivities are thus considered in the present simulation. The first case is Arrehenius-type impurity diffusion coefficient of liquid phase [15] (“Case 1”). The second is only considering the diagonal terms based on the atomic mobility database [16] (“Case 2”). The third is considering both the diagonal and cross terms (“Case 3”).
3.2 Results and discussion
Figure 1 compares the phase-field simulated morphologies of primary (Al) grain of three cases. As can be seen, the dendrite of “Case 1” is obviously thinner and sharper, compared with the other two cases. While the morphologies of dendrites in “Case 2” and “Case 3” are very similar. The solidified volume fractions of dendrites in three cases are compared in Fig. 2. As shown in the figure, the solidified volume fractions of dendrites in three cases increase smoothly over the simulation range. The solidified volume fraction of dendrite in “Case 2” is always slightly higher than that in “Case 3”, but both are much higher than that in “Case 1”. The tip velocities of the dendrites in the three cases are compared in Fig. 3. It can be seen in the figure that the general trend for the three cases is similar, that is, the tip velocity increases first, reaches a maximum at a certain time, and decreases after that. Furthermore, the tip velocities in both “Case 2” and “Case 3” are higher than that in “Case 1” over the “increase” range, while the case is the opposite in the “decrease” range.

Fig. 1 Comparison among phase-field simulated morphologies of primary (Al) grain during solidification in three cases at cooling rate of 2 K/s

Fig. 2 Comparison of solidified volume fractions of primary (Al) phase in three cases

Fig. 3 Comparison of tip velocities of (Al) dendrites in three cases
Figure 4 presents the comparison of the phase-field simulated concentration fields of Fe, Mg, Mn and Si at t= 4.05 s in the three cases. From the figure, the influence of different liquid diffusivities on concentration fields of different components can be clearly seen. The detail composition profiles of Fe, Mg, Mn and Si in (Al) dendrite and liquid phase ahead of the tip at t=4.05 s are compared in Fig. 5. An enlarged region for the liquid compositions ahead of the tip in three cases is also superimposed for each component. As can be seen in Fig. 5, the maximum liquid compositions of all the solutes in “Case 2” and “Case 3” are higher than those in “Case 1”. The reason is due to the fact that the curvature undercooling in “Case 1” is much higher than that in “Case 2” or “Case 3” because of its sharper tip in the dendrite. Moreover, the composition gradients for Fe, Mg and Mn are similar in the three cases, but for Si in “Case 1” it is much steeper than in “Case 2” or “Case 3”. The major reason lies in the fact that the contents of Fe, Mg and Mn are very small, and the related diagonal diffusivities from atomic mobility database are almost equal to the impurity diffusivities in “Case 1”, while the content of Si is much larger in the target alloy, and the diagonal diffusivities related to Si from the atomic mobility database are 2-3 times larger than the corresponding impurity diffusion coefficients. Moreover, the composition profiles for all the components in “Case 3” are generally steeper than those in “Case 2”, which is due to the contribution of the non-diagonal diffusion coefficients on the composition evolution. The main contribution is from the non-diagonal diffusivities related to Si because of its relatively larger value (in the magnitude of 10-5 cm2/s) and concentration gradient.
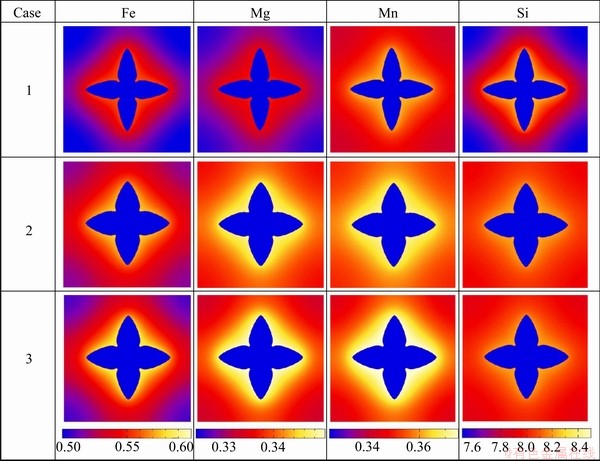
Fig. 4 Comparison of phase-field simulated concentration fields for different components in three cases at t=4.05 s

Fig. 5 Comparison of different concentration profiles in (Al) and liquid phases ahead of dendrite tip in three cases at t=4.05 s
In summary, the present phase-field simulation of solidification of primary phase in Al356.1 alloys indicates that different liquid diffusion coefficients can largely affect the morphology, the volume of the solidified phase, the tip velocity of the dendrites as well as the concentration fields of liquid phase ahead of the dendrites. It is indicated that some simple assumptions of liquid diffusion coefficients in numerical simulation may lead to unreasonable results. Consequently, accurate atomic mobility database for liquid phase is highly needed for the quantitative simulation of solidification process in multicomponent alloys.
4 Conclusions
1) By fixing other thermophysical and numerical parameters, three cases of liquid diffusion coefficients were employed to study the effect of liquid diffusion coefficients on the microstructure evolution during solidification of primary (Al) phase in Al356.1 alloy by means of the phase-field simulation using two sets of diffusion coefficients in liquid phase.
2) The simulation results indicate that different liquid diffusion coefficients can largely influence the morphology, the volume of the solidified phase, the tip velocity of the dendrites as well as the concentration fields of liquid phase ahead of the dendrites.
3) An accurate liquid atomic mobility database is highly needed for a quantitative simulation of solidification process in multicomponent alloys.
References
[1] CHEN L Q. Phase-field models for microstructure evolution [J]. Annual Review of Materials Research, 2002,32:113-140.
[2] BOETTINGER W J, WARREN J A,BECKERMANNC, KARMA A. Phase-field simulationofsolidification [J].Annual Review of Materials Research,2002,32: 163-194.
[3] MOELANS N, BLANPAIN B, WOLLANTS P. An introduction to phase-field modeling of microstructureevolution [J]. CALPHAD, 2008, 32:268-294.
[4] STEINBACH I. Phase field models in materials science [J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17:073001-073031.
[5] STEINBACH I. Phase field model for microstructure evolution at the mesoscopic scale [J]. Annual Review of Materials Research, 2013, 43: 89-107.
[6] STEINBACH I, BOETTINGER B, EIKEN J, WARNKEN N, FRIES S G. CALPHAD and phase-field modeling: A successful liaison [J]. Journal ofPhase Equilibrium Diffusion, 2007,28:101-106.
[7] FRIES S G, BOETTINGER B, EIKEN J, STEINBACH I. Upgrading CALPHAD to microstructure simulation: The phase-field method [J]. International Journal of Materials Research, 2009,100:128-134.
[8] ZHANG L J, STEINBACH I, DU Y. Phase-field simulation of diffusion couples in the Ni-Al system [J]. International Journal of Materials Research, 2011, 102: 371-380.
[9] ZIVKOVIC D, TALIJAN N, KOSTOV A, BALANOVIC L J. Calculation of thermodynamic properties in liquid phase for ternary Al-Ni-Zn alloys [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 3059-3065.
[10] ZHANG S Z, ZHANG R J, QU X H, FANG W, LIU M Z. Phase-field simulation for non-isothermal solidification of multicomponent alloys coupled with thermodynamic database [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 2361-2367.
[11] RAVINDRA B, SENTHIL KUMAR T, BALASUBRAMANIAN V. Fatigue life prediction of gas metal arc welded cruciform joints AA7075 aluminum alloy failing from root region [J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 1210-1217.
[12]  ,CHENQ.DatabasesreleasedbyThermo-CalcSoftwareCompanyAB[EB/OL]. [2013-10-25]. http://www.thermocalc. com/ products-services/databases.
,CHENQ.DatabasesreleasedbyThermo-CalcSoftwareCompanyAB[EB/OL]. [2013-10-25]. http://www.thermocalc. com/ products-services/databases.
[13] DU Y, ZHANG L J, CUI S L, ZHAODD, LIU D D, ZHANG W B, SUN WH JIE W Q. Atomic mobilities and diffusivities in Alalloys [J]. Science China: Technological Sciences, 2012, 55: 306-328.
[14] ZHANG L J, DU Y, STEINBACH I, CHEN Q, HUANG B Y. Diffusivities of an Al-Fe-Ni melt and their effects on the microstructure during solidification [J]. ActaMaterialia, 2010, 58: 3664-3675.
[15] DU Y, CHANG Y A, HUANG B Y, GONG W P, JIN Z P, XU H H, YUAN Z H, LIU Y, HE Y H, XIE F Y. Diffusion coefficients of some solutes in FCC and liquid Al: Critical evaluation and correlation [J]. Materials Science and Engineering A, 2003, 363: 140-151.
[16] ZHANG R J, JING T, JIE W Q, LIU B C. Phase-field simulation of solidification in multicomponent alloys coupled with thermodynamic and diffusion mobility databases [J]. ActaMaterialia, 2006, 54: 2235-2239.
[17] DUY,LIU S H, ZHANG L J, XU H H, ZHAO D D, WANG A J, ZHOU L C. An overview on phase equilibria and thermodynamic modeling in multicomponent Al alloys: Focusing on the Al-Cu-Fe- Mg-Mn-Ni-Si-Zn system [J]. CALPHAD, 2011, 35: 427-445.
[18] STEINBACHI,APELM.MICRESStheMICRostructureEvolutionSimulation Software [EB/OL]. [2013-10-25]. http://web.access. rwth-aachen.de/ MICRESS.
[19] WANG S Q, LIU D D, DU Y, ZHANG L J, CHEN Q, ENGSTROEM A. Development of an atomic mobility database for liquid phase in multicomponent Alalloys: Focusing on binary systems [J]. International Journal of Materials Research, 2013, 104: 721-735.
[20] EIKEN J, BOETTGER B, STEINBACH I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application [J]. Physical Review E, 2006, 73: 066122-066131.
[21] DU Y, CHANG Y A, LIU S H, HUANG B Y, XIE F Y, YANG Y, CHEN S L. Thermodynamic description of the Al-Fe-Mg-Mn-Si system and investigation of microstructure and microsegregation during directional solidification of an Al-Fe-Mg-Mn-Si alloy [J]. Zeitschrift fuer Metallkunde, 2005, 96: 1351-1362.
[22] GUENDUEZ M, HUNT J D. The measurement of solid-liquid surface energies in the Al-Cu, Al-Si and Pb-Sn systems [J]. Acta Metallurgica, 1985, 33(9): 1651-1672.
[23] NAPOLITANO R E. Experimental measurement of anisotropy in crystal melt interfacial energy [J]. Interface Science, 2002, 10: 217-232.
液相扩散系数对Al356.1合金凝固过程显微组织演变的影响
孙伟华1,2,张利军1,2,魏 明1,2,杜 勇1,2,黄伯云1
1. 中南大学 粉末冶金国家重点实验室,长沙 410083;
2. 中南大学 中德铝合金微结构联合实验室,长沙 410083
摘 要:采用相场方法研究了液相扩散系数对Al356.1合金凝固过程初晶(Al)相显微组织演变的影响。在相场模拟中,采用了两套液相扩散系数,而其他热物理参数和数值参数则保持一致。第一套液相扩散系数只考虑随温度变化的Arrhenius类型的杂质扩散系数,而第二套则为随温度和成分变化的精准的液相原子移动性数据库。对于第二套液相扩散系数,还分析了扩散系数矩阵中的非对角项对Al356.1 合金凝固过程中显微组织演变的影响。通过相场模拟发现:在3种液相扩散系数情况下,初晶(Al)相的形貌、枝晶尖端的速率和枝晶前端的成分曲线均有不同。研究结果表明:精确的液相原子移动性参数对定量模拟凝固过程显微组织演变是非常重要的。
关键词:Al356.1合金;凝固;显微组织演变;扩散系数;相场模拟
(Edited by Hua YANG)
Foundation item: Projects (51021063, 51301208) supported by the National Natural Science Foundation of China; Project (GZ755) supported by Sino-German Center for Promotion of Science; Project (2011CB610401) supported by the National Basic Research Program of China; Project supported by Shenghua Scholar Program of Central South University, China
Corresponding author: Li-jun ZHANG; Tel: +86-731-88877963; Fax: +86-731-88710855; E-mail: xueyun168@gmail.com; lijun.zhang@csu.edu.cn
DOI: 10.1016/S1003-6326(13)62922-2