两相区各相激活能对Zr-2.5Nb-0.5Cu合金本构方程的影响
来源期刊:中国有色金属学报(英文版)2017年第1期
论文作者:K. K. SAXENA S. K. JHA V. PANCHOLI G. P. CHAUDHARI D. SRIVASTAVA G. K. DEY N. SAIBABA
文章页码:172 - 183
关键词:Zr-2.5Nb-0.5Cu合金;热变形;激活能;本构方程;两相材料
Key words:Zr-2.5Nb-0.5Cu alloy; hot deformation; activation energy; constitutive equation; two-phase material
摘 要:通过计算Zr-2.5Nb-0.5Cu合金两相区各相激活能,研究该合金在热变形过程中的主要存在相。在温度为700~925 °C、应变速率为10-2~10-3 s-1的条件下对Zr-2.5Nb-0.5Cu合金进行热机械压缩实验。单相流动应力推广用于两相区各相流动应力的计算,然后利用所得两相区流动应力数据来计算各相的激活能。对计算所得激活能数据进行比较可知,α相为两相区的主要相(形变控制相)。根据形变温度范围或各相存在形式,采用正弦双曲线型本构方程建立了合金的本构方程。统计学分析结果表明,从相关系数(R)和平均相对误差(AARE)考虑,采用为某特定相建立的本构方程所得计算结果与实验结果相符。
Abstract: Dominant phase during hot deformation in the two-phase region of Zr-2.5Nb-0.5Cu (ZNC) alloy was studied using activation energy calculation of individual phases. Thermo-mechanical compression tests were performed on a two-phase ZNC alloy in the temperature range of 700-925 °C and strain rate range of 10-2-10 s-1. Flow stress data of the single phase were extrapolated in the two-phase range to calculate flow stress data of individual phases. Activation energies of individual phases were then calculated using calculated flow stress data in the two-phase range. Comparison of activation energies revealed that α phase is the dominant phase (deformation controlling phase) in the two-phase range. Constitutive equations were also developed on the basis of the deformation temperature range (or according to phases present) using a sine-hyperbolic type constitutive equation. The statistical analysis revealed that the constitutive equation developed for a particular phase showed good agreement with the experimental results in terms of correlation coefficient (R) and average absolute relative error (AARE).
Trans. Nonferrous Met. Soc. China 27(2017) 172-183
K. K. SAXENA1,4, S. K. JHA2, V. PANCHOLI1, G. P. CHAUDHARI1, D. SRIVASTAVA3, G. K. DEY3, N. SAIBABA2
1. Department of Metallurgical and Materials Engineering, Indian Institute of Technology, Roorkee-247667, Uttarakhand, India;
2. Nuclear Fuel Complex Limited, Hyderabad-501301, India;
3. Materials Science Division, Bhabha Atomic Research Center, Mumbai-40085, India;
4. Department of Mechanical Engineering, Insitute of Engineering and Technology, GLA Uinversity, Mathura-281406, Uttar Pradesh, India
Received 16 January 2016; accepted 6 May 2016
Abstract: Dominant phase during hot deformation in the two-phase region of Zr-2.5Nb-0.5Cu (ZNC) alloy was studied using activation energy calculation of individual phases. Thermo-mechanical compression tests were performed on a two-phase ZNC alloy in the temperature range of 700-925 °C and strain rate range of 10-2-10 s-1. Flow stress data of the single phase were extrapolated in the two-phase range to calculate flow stress data of individual phases. Activation energies of individual phases were then calculated using calculated flow stress data in the two-phase range. Comparison of activation energies revealed that α phase is the dominant phase (deformation controlling phase) in the two-phase range. Constitutive equations were also developed on the basis of the deformation temperature range (or according to phases present) using a sine-hyperbolic type constitutive equation. The statistical analysis revealed that the constitutive equation developed for a particular phase showed good agreement with the experimental results in terms of correlation coefficient (R) and average absolute relative error (AARE).
Key words: Zr-2.5Nb-0.5Cu alloy; hot deformation; activation energy; constitutive equation; two-phase material
1 Introduction
Constitutive equation describes the relationship between stress, strain rate and deformation temperature. It helps to calculate expected load and power required for forming processes and also suggest material flow behavior [1]. Thus, it is necessary to develop an accurate constitutive equation for a given material. The constitutive equations are classified into three different categories: physical-based constitutive model, phenomenological constitutive model and artificial neural network (ANN). Physical-based models are based on physical aspects of material behaviors, i.e., theory of thermodynamics, kinetics of slip and thermally activated dislocation movement. These models are applicable over a wide range of loading conditions. Few physical-based models are Bodner-Partom (BP) model [2], Rusinek- Klepaczko (RK) model [3], Zerilli and Armstrong (ZA) model [4,5] and its modification (m-ZA) [6], Preston- Tonks-Wallace (PTW) model [7], Voyiadjis-Almasri (VA) model [8] and cellular automaton (CA) model [9,10]. In phenomenological models, a description of flow stress is based on empirical observations using some mathematical functions. These models are suitable where an exact physical mechanism is not clear. However, these are applicable over a limited range of strain rate and temperature. Few phenomenological models are: Voce- Kocks (VK) model [11], Johnson-Cook (JC) model [12], and its modification (m-JC) [6], Khan-Zhang-Takacs (KZT) model [13], Farrokh-Khan (FK) model [14], Molinari-Ravichandran (MR) model [15], Arrhenius type model with or without strain compensation [16-18], and its modified model [19]. Lastly, ANN provides an alternative approach to predict flow behavior during hot deformation, and it is best suitable to those problems for which material behavior is not clear at all. But, the successful application of ANN model is strongly based on error free data and characteristic variables. Out of all the approaches, phenomenological models are widely used models because they offer a trade-off between knowing exact material behavior and “black box” approach of ANN. SELLARS and TEGART [20] and JONAS et al [21] have proposed a phenomenological approach, in which flow stress is related to the strain rate by sine-hyperbolic law in Arrhenius type equation. Extensive work on constitutive analysis of hot deformation for different metals and alloys was reported by LIN and CHEN [22], CINGARA and McQUEEN [23][35], PHANIRAJ et al [24,25], KASSAM et al [26], MIRZADEH et al [18,27,28], and SAMANTARAY et al [29]. The flow stress of a material depends upon both strain rate and temperature which can be combined in a single parameter known as Zener-Hollomon parameter (Z) [30]. However, the influence of temperature and strain rate on the flow behavior of two-phase (HCP/BCC) alloys such as Zr-2.5Nb-0.5Cu (ZNC) is not well understood.
Irrespective of the model used, the development of a constitutive equation for a two-phase material becomes even more complicated due to uncertainty in determining the dominant phase in the two-phase range. Accurate determination of activation energy, stress exponent and pre-exponential factor is important to develop an accurate constitutive equation. Thus, it is essential to understand activation energies of individual phases in the two-phase range. In literature, different approaches were used to calculate the activation energy for deformation of two-phase materials. KIM et al [31] considered activation energy on the basis of the strain rate range for deformation of the two-phase Ti-6Al-4V alloy. KOTKUNDE et al [19,32], YUAN et al [33] and ZHANG et al [34] compared constitutive models for various Ti alloys irrespective of the phases present. CHEN et al [35] developed constitutive models of Ti-6Al-4V alloy in the temperature range 20-900 °C (below β transus temperature), without considering the effect of phases present. WEI et al [36] reported a single activation energy of a dual-phase Mg-Li alloy for the entire range of deformation temperatures. QIN et al [37] calculated common activation energy for TC11/Ti- 22Al-25Nb dual-phase alloy, without considering the effect of alloy as well as the phases present in the alloy. BALASUNDAR et al [38] calculated single activation energy of near-α titanium alloy IMI834 having duplex microstructure, whereas WANJARA et al [39] calculated two activation energies of the same alloy; one for the two-phase (i.e., (α+β) phase) and the other for the single phase β. SESHACHARYULU et al [40], PORNTADAWIT et al [41] for Ti-6Al-4V alloy, and SARKAR and CHAKRAVARTTY [42] for Zr-1Nb alloy considered the activation energies of two-phase and single phase separately and found that the activation energy of the two-phase (α+β) is higher than that of the single phase β. In summation, we can say that there are two approaches used by researchers: 1) a single activation energy for the entire range of deformation temperature covering both single and the two-phase region or; 2) two activation energies according to the phases present, i.e., one for two-phase (α+β) and the other for single phase α or β. From the above literature review, it is clear that the calculation of activation energy and other parameters of a constitutive equation for two-phase materials requires systematic approach.
In the present work, different sets of flow stress data were considered to develop constitutive equations: one set belongs to experimental data, and the other set of flow stress was calculated from the experimental values in a two-phase range. Using each set of flow stress data, independent constitutive equations were developed for: 1) in deformation temperature range from 700 to 815 °C, related to (α+β) phase, 2) in deformation temperature from 815 to 925 °C related to β phase, 3) entire range of deformation temperature, i.e., from 700 to 925 °C related to (α+β) and β phase (or complete data set irrespective of phases present) and, 4) from the calculated flow stress values of individual phases (i.e., individual α or β phase) in (α+β) phase range. To evaluate developed constitutive equations, statistical analysis was applied to experimental and predicted peak flow stress values.
2 Experimental
The material used for this study is Zr-2.5Nb-0.5Cu (ZNC) alloy. It was initially in the form of extruded billet that was β-quenched. From billet, cylindrical specimens of 15 mm in height and 10 mm in diameter were machined in such a manner that the compression axis of the specimens was along the extrusion direction. For the compression test specimen, concentric grooves of about 0.5 mm in depth were provided on the end surfaces and a nickel-based lubricant along with a graphite sheet was used between the specimen and the crosshead of anvil to reduce friction during compression. A thermocouple was attached at the center of the specimen to measure the specimen temperature as well as adiabatic temperature rise during compression at high strain rates (i.e., 1 s-1 and above). The isothermal compression tests were carried out on a Gleeble-3800 (Thermo-mechanical simulator) in a temperature range of 700-925 °C and strain rate of 10-2-10 s-1, to investigate the hot deformation behavior of the material. The samples were initially heated to desired temperatures at a rate of 5 °C/s, and then soaked for 300 s. All specimens were deformed up to a true strain of 0.69 and then quenched. During a hot compression test, the flow stress data were recorded automatically as a function of strain for each deformation temperature and strain rate from the computer interface of Gleeble-3800
(Thermo-mechanical simulator) in a temperature range of 700-925 °C and strain rate of 10-2-10 s-1, to investigate the hot deformation behavior of the material. The samples were initially heated to desired temperatures at a rate of 5 °C/s, and then soaked for 300 s. All specimens were deformed up to a true strain of 0.69 and then quenched. During a hot compression test, the flow stress data were recorded automatically as a function of strain for each deformation temperature and strain rate from the computer interface of Gleeble-3800 .
.
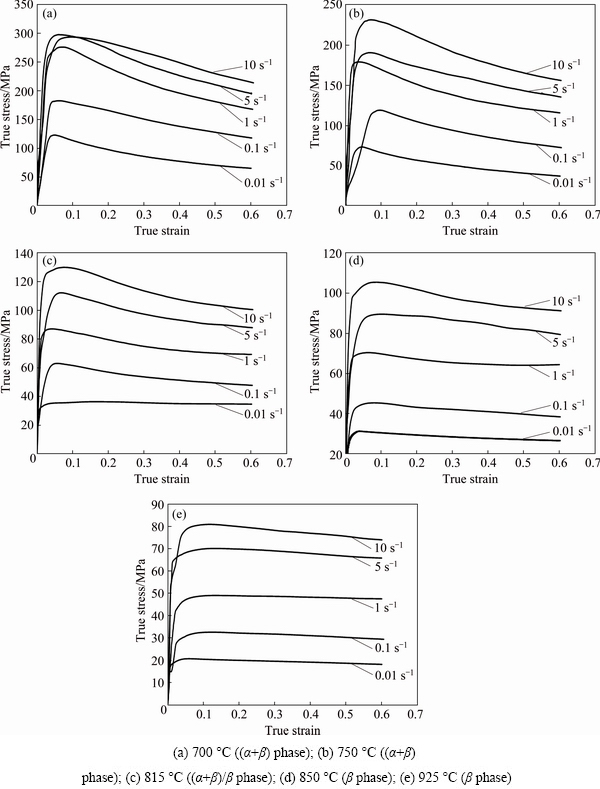
Fig. 1 True stress-true strain curves of ZNC alloys at different deformation temperatures
3 Results
3.1 Stress-strain relationship
Figure 1 shows the true stress-true strain curves of ZNC alloys obtained after correction for an adiabatic temperature rise at high strain rates (i.e., 1 s-1 and above), deformation temperatures of 700-925 °C and strain rates of 10-2-10 s-1. According to lever rule, the proportion of α/β phase should vary with the deformation temperature. Hence, flow behavior should reveal the dominance of a particular phase on the deformation mechanism at different temperatures. Figures 1(a) and (b) show that the degree of flow softening decreases with an increase in deformation temperature (decrease in α-phase proportion) for all strain rates used. It appears that flow softening is due to DRX in α phase [43] and its effect on flow behavior decreases with an increase in the temperature (or increase in proportion of β phase), more or less similar to Zr-2.5Nb alloy [44]. In the temperature range of 850-925 °C (β-phase), the flow stress curves show a steady state behavior for all strain rates used except under conditions of 850 °C (5 and 10 s-1) and 925 °C (10 s-1).
3.2 Establishment of constitutive equations
The development of the constitutive equation allows extrapolation of flow stress data beyond the test window. An Arrhenius type equation was proposed to relate flow stress with strain rate and temperature.
Usually, all materials exhibit an increase in flow stress with an increase in strain rate and decrease in temperature. The flow stress behavior depends on the generation rate of defects and their removal by thermally activated processes. ZENER and HOLLOMON [30] proposed a single parameter (Z) to express flow stress as a function of strain rate and temperature. Zener- Hollomon parameter (Z) can be defined in terms of temperature (T) and strain rate 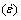 , as shown in Eq. (1) [29].
, as shown in Eq. (1) [29].
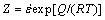 (1)
(1)
In Arrhenius equation, the strain rate is a common parameter related to the deformation temperature and activation energy. Thus, the strain rate is generally expressed by one of the three different types of equations: the power law (Eq. (2)), the exponential law (Eq. (3)) and sine-hyperbolic law (Eq. (4)). The applicability of each equation depends upon the stress value. It is reported that the power law equation “breaks down” at high stress values, therefore, it is valid for low stress values, i.e., ασ<0.8 (Eq. (2)). On the other hand, the exponential law equation is valid at high stress values, i.e., ασ>1.2 (Eq. (3)) [45]. However, a sine-hyperbolic law equation (Eq. (4)) is valid for a wider range of flow stress and more commonly in use [20,46].
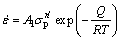 (2)
(2)
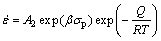 (3)
(3)
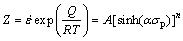 (4)
(4)
where A, A1, A2, n and n′ are material constants, Q is the activation energy for hot deformation (kJ/mol), R is the universal gas constant (8.314 J/(mol·K) and T is the thermodynamic temperature (K). One additional adjustable constant is α, known as stress multiplier. It brings ασ into the correct range to make 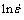 versus ln[sinh(ασp)] curves linear and parallel.
versus ln[sinh(ασp)] curves linear and parallel.
Under a particular deformation condition of strain rate and temperature, flow stress is a function of strain. Therefore, for the development of a constitutive equation, either peak stress (strain can vary) or stress value at a constant strain is considered. Stress values other than peak stress may vary due to softening or hardening mechanisms and may not be obtained accurately [47]. Thus, it is better to use peak stress values to determine a constitutive equation [23,48]. Also, peak stress is uniquely related to Zener-Hollomon parameter (Z), in the entire range of deformation conditions [49]. Additionally, peak stress is more important for industrial processes [50]. In this study, peak flow stress was considered to develop sine-hyperbolic law equation.
3.3 Identification of material parameters
The sine-hyperbolic law constitutive equation requires the determination of few material constants, i.e., A, n, α and Q. These material constants can be obtained as follows.
3.3.1 Determination of α value
The value of α can be calculated by α(≈β/n′) [45], where n′ and β can be calculated from Eqs. (2) and (3). Taking natural logarithm on both sides of Eqs. (2) and (3) yields Eqs. (5) and (6), respectively.
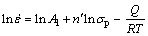 (5)
(5)
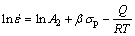 (6)
(6)
The partial differentiations of Eqs. (5) and (6) with respect to peak flow stress (σp) at constant temperature yield
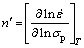 (7)
(7)
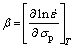 (8)
(8)
where constants β and n′ can be calculated using linear regression of the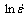 vs σp plot and the plot of
vs σp plot and the plot of 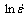 vs ln σp, respectively, at each temperature as shown in Figs. 2(a) and (b). The final values of parameters n′ and β are their average values calculated from the slopes obtained at each temperature. For present ZNC alloy, the values of parameters n′, β and α are summarized in Table 1.
vs ln σp, respectively, at each temperature as shown in Figs. 2(a) and (b). The final values of parameters n′ and β are their average values calculated from the slopes obtained at each temperature. For present ZNC alloy, the values of parameters n′, β and α are summarized in Table 1.
3.3.2 Determination of n
The value of n can be calculated using Eq. (4). Simplification of Eq. (4) using natural logarithm on both sides yields Eq. (9). Partial differentiation of Eq. (9) with respect to peak flow stress at constant temperature results in Eq. (10):
 (9)
(9)
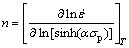 (10)
(10)
The relationship between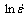 and ln[sinh(ασp)] is plotted in Fig. 3(a) at constant temperature. Thereafter, the final n value is an average slope value of all temperatures and summarized in Table 1.
and ln[sinh(ασp)] is plotted in Fig. 3(a) at constant temperature. Thereafter, the final n value is an average slope value of all temperatures and summarized in Table 1.
3.3.3 Determination of activation energy (Q)
For high temperature deformation, activation energy (Q) can be obtained by rearranging Eq. (9) as follows:
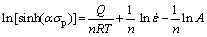 (11)
(11)
The partial differentiation of Eq. (11) at constant strain rate with respect to the reciprocal of deformation temperature (1/T) yields Eq. (12):
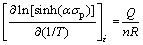 (12)
(12)
Table 1 Calculated material constants of ZNC alloy for various phases
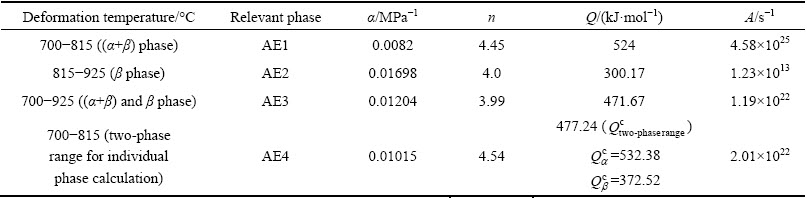
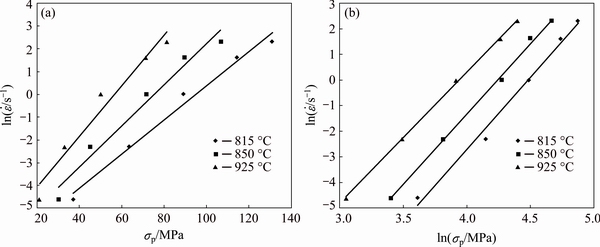
Fig. 2 Plots to obtain values of β (a) and n′ (b)
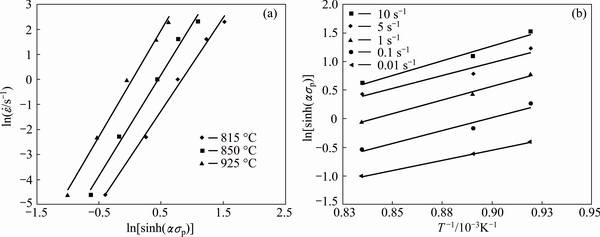
Fig. 3 Plots to calculate values of n (a) and S (b)
Therefore, the activation energy can be defined as follows:
Q=RnS (13)
where  .
.
S is determined by linear regression of ln[sinh(ασp)] vs (1000/T) plots at constant strain rates, as shown in Fig. 3(b). Afterwards, the final value of S is an average of slope values obtained at different strain rates. By using the average values of n and S in Eq. (13), final activation energy can be calculated.
3.3.3.1 Activation energies in different temperature domains
The phase diagram of the studied ZNC alloy is more or less similar to that of Zr-2.5Nb alloy. Due to the addition of Cu into Zr-2.5Nb, its hexagonal closed packed (HCP) α-Zr phase is stable up to 630 °C (±10 °C) and body centered cubic (BCC) phase β-Zr is stable at high temperatures above 825 °C (±10 °C). In the intermediate temperature range it has a two-phase range, i.e., (α+β) phase [51]. It is expected that the activation energy of hot deformation may show two entirely different values, depending upon the dominant phase in the two-phase region. Therefore, in the present work, activation energy calculations were done according to the deformation temperature range (or domain). Thus, three different activation energies were calculated: AE1 for a deformation temperature from 700 to 815 °C related to (α+β) phase, AE2 for deformation temperature from 815 to 925 °C related to β phase, and AE3 is in the entire range of deformation temperature, i.e., from 700 to 925 °C related to (α+β) and β phases. Thus, the calculated activation energies using peak flow stress for different temperature ranges are as follows: AE1 is 524 kJ/mol, AE2 is 300.17 kJ/mol, and AE3 is 471.67 kJ/mol.
3.3.3.2 Activation energy of individual phases in two- phase range
Unlike single phase material, activation energy of a two-phase material cannot be related directly to the operating deformation mechanism [52]. However, if the contribution of individual phases can be separated, one can estimate deformation parameters of the phases present. To determine the contribution of individual phases during hot deformation in the two-phase range, it is necessary to calculate activation energies of individual phases. To obtain the flow stress of individual α phase (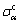 ) and β phase (
) and β phase ( ), flow stress values from single phase β (
), flow stress values from single phase β (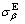 ) were extrapolated in the two-phase range. Assuming equi-strain rate condition, i.e., stress is distributed among their constituent phases according to their phase fraction, as expressed in Eq. (14), flow stress values of α phase were calculated:
) were extrapolated in the two-phase range. Assuming equi-strain rate condition, i.e., stress is distributed among their constituent phases according to their phase fraction, as expressed in Eq. (14), flow stress values of α phase were calculated:
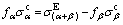 (14)
(14)
where 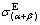 is an experimental flow stress in the two-phase range; fα, fβ and
is an experimental flow stress in the two-phase range; fα, fβ and  are fractions and calculated flow stresses of individual α and β phases in the two-phase range, respectively. After getting the stress values of individual α and β phases,
are fractions and calculated flow stresses of individual α and β phases in the two-phase range, respectively. After getting the stress values of individual α and β phases, 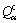 and
and 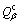 were calculated using the same procedure as described in earlier sections. After calculating activation energies of individual phases, the activation energy of the composite microstructure containing both the phases was calculated using analysis proposed by BRIOTTET et al [52] as described in Eq. (15)
were calculated using the same procedure as described in earlier sections. After calculating activation energies of individual phases, the activation energy of the composite microstructure containing both the phases was calculated using analysis proposed by BRIOTTET et al [52] as described in Eq. (15)
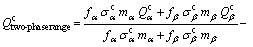
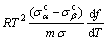 (15)
(15)
where m and σ are the average values of strain rate sensitivity and flow stress of individual phases, respectively. The first term on the right hand side of Eq. (15) represents the weighted average of 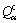 and
and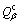 , which is normalized by factor fσm of each phase. The second term on the right hand side is a product of two terms: one includes the difference between the flow stresses of individual phases at a particular temperature, and the other is the first derivative of the fraction of any individual phase with respect to temperature. The calculated activation energies of
, which is normalized by factor fσm of each phase. The second term on the right hand side is a product of two terms: one includes the difference between the flow stresses of individual phases at a particular temperature, and the other is the first derivative of the fraction of any individual phase with respect to temperature. The calculated activation energies of 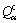 and
and 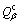 are 532.38 and 372.52 kJ/mol, respectively, whereas activation energy
are 532.38 and 372.52 kJ/mol, respectively, whereas activation energy 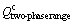 for a two-phase range is 477.24 kJ/mol.
for a two-phase range is 477.24 kJ/mol.
3.3.4 Determination of constant A
The linear regression of the 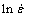 vs ln[sinh(ασp)] plots from Eq. (10) at each temperature can provide the intercept value to calculate constant A, as shown in Fig. 3(a). Furthermore, A can be calculated by following equations:
vs ln[sinh(ασp)] plots from Eq. (10) at each temperature can provide the intercept value to calculate constant A, as shown in Fig. 3(a). Furthermore, A can be calculated by following equations:
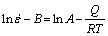 (16)
(16)
where B is the interception of Eq. (10).
Simplifying Eq. (16) yields Eq. (17)
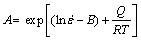 (17)
(17)
Since the value of Q is already obtained. ln A was determined using the intercept of the linear regression of the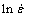 vs ln[sinh(ασp)] plot at each temperature. Afterwards, the average value of ln A for all ranges of deformation temperature was obtained.
vs ln[sinh(ασp)] plot at each temperature. Afterwards, the average value of ln A for all ranges of deformation temperature was obtained.
3.4 Microstructural observation
Figure 4 shows the microstructure of as-received material. The microstructure reveals equiaxed grains having an average grain size of 200 μm. Since the material is β-quenched, microstructure shows fine plates of α-surrounded by prior β grain boundaries. Figure 5 shows the microstructure of a sample deformed at temperature of 750 °C and strain rate of 1×10-2 s-1, whereas Fig. 6 shows the microstructure of a sample deformed at temperature of 815 °C and strain rate of 1×10-1 s-1. These two deformation temperatures fall in the two-phase region. However, the temperature of 815 °C is very close to β transus temperature. Both the microstructures show recrystallized, globular α phase and transformed β phase (indicated by arrows).

Fig. 4 Microstructure of as-received (β-quenched) Zr-2.5Nb-0.5Cu alloy

Fig. 5 Microstructure of sample deformed at temperature of 750 °C and strain rate of 1×10-2s-1 (Compression direction is vertical)

Fig. 6 Microstructure of sample deformed at temperature of 815 °C and strain rate of 1×10-1s-1(Compression direction is vertical)
4 Discussion
4.1 Apparent activation energy and deformed microstructure
The apparent activation energy of hot deformation depends upon the rate controlling process, i.e., the slowest process. It is determined using peak stress as a function of temperature at a constant strain rate with the assumption that the microstructure remains unchanged. By comparing the apparent activation energy values with the true activation energy values of different diffusion processes, the dominant deformation mechanism can be predicted. Usually, the two activation energies are quite different since apparent activation energy depends upon alloying element, ease of dislocation glide or climb and grain size. The apparent activation energy calculated from hot deformation data is usually much higher than the true activation energy calculated from atomic diffusion mechanisms [45]. DYMENT and LIBANATI [53] reported that the true activation energies are approximately half of that predicted by semi-empirical relations based on physical properties. For example, the apparent activation energy value calculated in this work is in the range of 300-524 kJ/mol, whereas true activation energy values are 112.97 kJ/mol for self-diffusion of pure Zr, 92.89 kJ/mol for the diffusion of Zr in Zr-Nb alloys, while the activation energy for diffusion of Nb in Zr is 131.80 kJ/mol. Activation energy (AE4) calculated for individual phase in the two-phase range suggests that the diffusion in α phase is slower than that in β phase. Therefore, α phase should dominate hot deformation in the two-phase range. Additionally, the activation energy (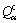 ) of individual α phase, i.e., 532.38 kJ/mol is also very close to the activation energy (AE1) of the two-phase range, i.e., 524 kJ/mol determined from experimental data.
) of individual α phase, i.e., 532.38 kJ/mol is also very close to the activation energy (AE1) of the two-phase range, i.e., 524 kJ/mol determined from experimental data.
The values of stress exponent calculated in Section 3.3.2 and shown in Table 1 for different modes of calculation, indicate that the values of stress exponents lie in the range from 3.99 to 4.5. The value of the stress exponent below or equal to 5 suggests that the deformation mechanism during the hot deformation of ZNC alloy is controlled by glide and climb of dislocation (climb controlled) [42,54]. For climb-controlled deformation mechanism, the activation energy should be close to the activation energy of lattice diffusion [55-61]. However, the values of activation energy determined from experimental data in the present work are much higher than that of lattice diffusion. Therefore, we used experimentally determined activation energy values to develop constitutive equations instead of the activation energy value of lattice diffusion.
According to BRIOTTET et al [52], an alloy can be categorized as T-type (titanium) if it shows greater flow stresses for a lower temperature phase than higher temperature phase over the entire two-phase range and the calculated activation energy Q(two-phase range) should be greater than the weighted averages of 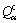 and
and 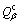 . For the present alloy,
. For the present alloy, 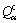 and
and 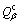 were obtained as 532.38 and 372.518 kJ/mol, respectively and the weighted average of
were obtained as 532.38 and 372.518 kJ/mol, respectively and the weighted average of 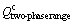 is 398.95 kJ/mol, which is less than the calculated
is 398.95 kJ/mol, which is less than the calculated 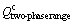 (477.239 kJ/mol) in the two-phase range. This confirms that the hot deformation behavior of Zr-Nb alloy is similar to that of Ti alloys.
(477.239 kJ/mol) in the two-phase range. This confirms that the hot deformation behavior of Zr-Nb alloy is similar to that of Ti alloys.
4.2 Verification of predicted peak stress
In order to validate the calculated material parameters, calculated peak flow stresses were compared with the experimental peak flow stresses. Applying a sine-hyperbolic law equation (Eq. (4)), a general expression to predict peak flow stress of a material can be obtained by using Eq. (18):
 (18)
(18)
As described earlier, constitutive analysis of hot deformation of Zr-2.5Nb-0.5Cu alloy was performed in four modes: AE1, AE2, AE3 and AE4. Thus, four different constitutive equations were developed to predict peak flow stress as follows:
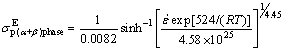 (19)
(19)
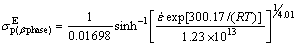 (20)
(20)
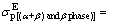
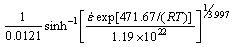 (21)
(21)
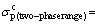
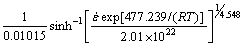 (22)
(22)
The predictability of a constitutive equation was also assessed employing standard statistical parameter such as correlation coefficient (R) and average absolute relative error (AARE).
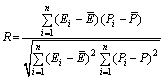 (23)
(23)
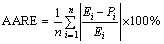 (24)
(24)
where P is the predicted value obtained using the constitutive equation and E is experimental value obtained from compression test, whereas 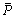 and
and 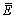 are the mean values of P and E, respectively. The total number of data employed during the investigation is represented by n.
are the mean values of P and E, respectively. The total number of data employed during the investigation is represented by n.
The correlation coefficient (R) is a commonly used statistical tool and provides information about the goodness of fit of a model with experimental values. The value of R lies in the range of 0 to 1. R near 1 represents that the regression line fits well with experimental values. However, this is not always true because of the bias in the data [33,62]. On the other hand, AARE provides a measure of term by term relative error and therefore is considered an unbiased statistical tool [33,63-65]. Thus, in this work, the verification of a constitutive equation was performed using AARE. Thus, the minimum value of AARE will indicate that a particular constitutive equation is able to capture the operating metallurgical processes. The values of R and AARE obtained for different constitutive equations are listed in Table 2 and shown in Fig. 7. AARE values are found to be very high for AE3 and comparable values for AE1, AE2 and AE4. Interestingly, R values for all equations are very close to each other.
Table 2 Values of R and AARE obtained for different constitutive equations
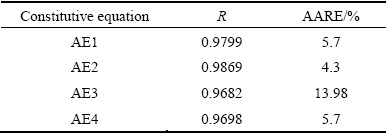
Constitutive equations developed for a (α+β) phase (AE1) and for a single β phase (AE2) show good agreement with experimental values. On the other hand, a constitutive equation developed for the entire range of deformation temperature 700-925 °C (AE3) predicts significant variation in peak flow stress values at higher strain rates and temperatures. This is due to clubbing of hot deformation data obtained from different phases.
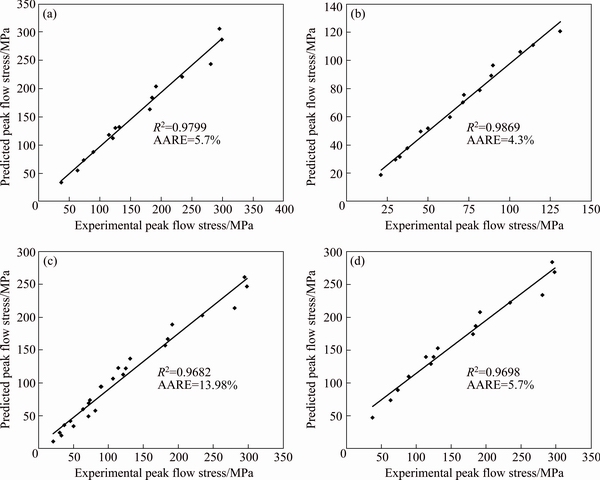
Fig. 7 Plots showing regression coefficient and AARE for AE1 (a), AE2 (b), AE3 (c) and AE4 (d)
Therefore, it is interesting to note that the constitutive equation for (α+β) phase (AE1) is able to predict peak stress though, the proportions of α and β phases must be significantly different at different deformation temperatures. A constitutive equation developed using calculated stress values for α and β phases by applying the rule of mixture (AE4) clarifies that the variation in proportion of the two-phase does not affect predictability of the equation developed. This brings out the fact that in a two-phase range deformation is dominated by only one of the phases.
5 Conclusions
1) Flow stress-strain curve revealed softening in the two-phase range, i.e., (α+β), whereas in the single β phase, it remains almost constant. Moreover, it is sensitive to deformation conditions (i.e., deformation temperatures and strain rates).
2) The activation energy of the two-phase range was found to be close to activation energy of the individual α phase, which clarifies that the dominant phase in the two-phase range of ZNC alloy is α phase. The microstructural observation also reveals that the dominated phase during hot deformation in the two phase range is α phase.
3) The constitutive equation (AE4) developed using calculated flow stress values for α 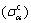 and β phases
and β phases 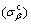 in two-phase range (α+β) phase, clarifies that the variation in the proportion of the two-phase does not affect the predictability of the developed equation. It also brings out that in two-phase range, deformation is dominated by only one of the phases, i.e., α phase for ZNC alloy.
in two-phase range (α+β) phase, clarifies that the variation in the proportion of the two-phase does not affect the predictability of the developed equation. It also brings out that in two-phase range, deformation is dominated by only one of the phases, i.e., α phase for ZNC alloy.
4) Constitutive equations developed for two-phase (α+β) range (AE1) and for a single phase β (AE2) show good agreement with experimental values, whereas the constitutive equation developed for the entire range of deformation temperature 700-925 °C (AE3) predicts significant variation in the values of peak flow stress at higher strain rates and higher temperatures. This is due to clubbing of hot deformation data obtained from different phases.
Acknowledgment
The authors acknowledge the financial support (Grant No. 2011/36/15) from Board of Research in Nuclear Science (BRNS), India.
References
[1] LIN Y C, XIA Y C, CHEN X M, CHEN M S. Constitutive descriptions for hot compressed 2124-T851 aluminum alloy over a wide range of temperature and strain rate [J]. Computational Materials Science, 2010, 50: 227-233.
[2] BODNER S R, PARTOM Y. Constitutive equations for elastic-viscoplastic strain-hardening materials [J]. Journal of Applied Mechanics, 1975, 42: 385-389.
[3] RUSINEK A, KLEPACZKO J R. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress [J]. International Journal of Plasticity, 2001, 17: 87-115.
[4] ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61: 1816-1825.
[5] MIRZAIE T, MIRZADEH H, CABRERA J M. A simple Zerilli–Armstrong constitutive equation for modeling and prediction of hot deformation flow stress of steels [J]. Mechanics of Materials, 2016, 94: 38-45.
[6] ZHANG H, WEN W, CUI H, XU Y. A modified Zerilli–Armstrong model for alloy IC10 over a wide range of temperatures and strain rates [J]. Materials Science and Engineering A, 2009, 527: 328-333.
[7] PRESTON D L, TONKS D L, WALLACE D C. Model of plastic deformation for extreme loading conditions [J]. Journal of Applied Physics, 2003, 93: 211-220.
[8] VOYIADJIS G Z, ALMASRI A H. A physically based constitutive model for fcc metals with applications to dynamic hardness [J]. Mechanics of Materials, 2008, 40: 549-563.
[9] JIN Zhao-yang, LIU Juan, CUI Zhen-shan, WEI Dong-lai. Identification of nucleation parameter for cellular automaton model of dynamic recrystallization [J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 458-464.
[10] GOETZ R L, SEETHARAMAN V. Modeling dynamic recrystallization using cellular automata [J]. Scripta Materialia, 1998, 38: 405-413.
[11] KOCKS U F. Laws for work-hardening and low-temperature creep [J]. Journal of Engineering Materials and Technology, 1976, 98: 76-85.
[12] JOHNSON G R, COOK W H. Constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Proceedings of the Seventh International Symposium on Ballistic. Hague, Netherlands, 1983: 541-547.
[13] KHAN A S, ZHANG H, TAKACS L. Mechanical response and modeling of fully compacted nanocrystalline iron and copper [J]. International Journal of Plasticity, 2000, 16: 1459-1476.
[14] FARROKH B, KHAN A S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling [J]. International Journal of Plasticity, 2009, 25: 715-732.
[15] MOLINARI A, RAVICHANDRAN G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length [J]. Mechanics of Materials, 2005, 37: 737-752.
[16] MARCHATTIWAR A, SARKAR A, CHAKRAVARTTY J K, KASHYAP B P. Dynamic recrystallization during hot deformation of 304 austenitic stainless steel [J]. Journal of Materials Engineering and Performance, 2013, 22: 2168-2175.
[17] LI J, XIA X. Modeling high temperature deformation behavior of large-scaled Mg-Al-Zn magnesium alloy fabricated by semi-continuous casting [J]. Journal of Materials Engineering and Performance, 2015, 24: 3539-3548.
[18] MIRZADEH H. A simplified approach for developing constitutive equations for modeling and prediction of hot deformation flow stress [J]. Metallurgical and Materials Transaction A, 2015, 46: 4027-4037.
[19] KOTKUNDE N, KRISHNAMURTHY H N, PURANIK P, GUPTA A K, SINGH S K. Microstructure study and constitutive modeling of Ti-6Al-4V alloy at elevated temperatures [J]. Materials & Design, 2014, 54: 96-103.
[20] SELLARS C M, TEGART W J. On the mechanism of hot deformation [J]. Acta Metallurgica, 1966, 14: 1136-1138.
[21] JONAS J J, SELLARS C M, TEGART W J M. Strength and structure under hot-working conditions [J]. Metallurgical Reviews, 1969, 14: 1-24.
[22] LIN Y C, CHEN X M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials & Design, 2011, 32: 1733-1759.
[23] CINGARA A, McQUEEN H J. New formula for calculating flow curves from high temperature constitutive data for 300 austenitic steels [J]. Journal of Materials Processing Technology, 1992, 36: 31-42.
[24] PHANIRAJ C, NANDAGOPAL M, MANNAN S L, RODRIGUEZ P. The relationship between transient and steady state creep in AISI 304 stainless steel [J]. Acta Metallurgica et Materialia, 1991, 39: 1651-1656.
[25] SAMANTARAY D, PHANIRAJ C, MANDAL S, BHADURI A K. Strain dependent rate equation to predict elevated temperature flow behavior of modified 9Cr-1Mo (P91) steel [J]. Materials Science and Engineering A, 2011, 528: 1071-1077.
[26] KASSAM Z H A, WANG Z, HO E T C. Constitutive equations for a modified Zr-2.5wt.%Nb pressure tube material [J]. Materials Science and Engineering A, 1992, 158: 185-194.
[27] MIRZADEH H. Constitutive description of 7075 aluminum alloy during hot deformation by apparent and physically-based approaches [J]. Journal of Materials Engineering and Performance, 2015, 24: 1095-1099.
[28] MIRZADEH H, CABRERA J M, NAJAFIZADEH A. Constitutive relationships for hot deformation of austenite [J]. Acta Materialia, 2011, 59: 6441-6448.
[29] SAMANTARAY D, MANDAL S, BHADURI A K, SIVAPRASAD P V. An overview on constitutive modelling to predict elevated temperature flow behaviour of fast reactor structural materials [J]. Trans Indian Inst Met, 2010, 63: 823-831.
[30] ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel [J]. Journal of Applied Physics, 1944, 15: 22-32.
[31] KIM J H, SEMIATIN S L, LEE C S. Constitutive analysis of the high-temperature deformation of Ti-6Al-4V with a transformed microstructure [J]. Acta Materialia, 2003, 51: 5613-5626.
[32] KOTKUNDE N, DEOLE A D, GUPTA A K, SINGH S K. Comparative study of constitutive modeling for Ti-6Al-4V alloy at low strain rates and elevated temperatures [J]. Materials & Design, 2014, 55: 999-1005.
[33] YUAN Z, LI F, QIAO H, XIAO M, CAI J, LI J. A modified constitutive equation for elevated temperature flow behavior of Ti-6Al-4V alloy based on double multiple nonlinear regression [J]. Materials Science and Engineering A, 2013, 578: 260-270.
[34] ZHANG C, LI Xiao-qiang, LI Dong-sheng, JIN Chao-hai, XIAO Jun-jie. Modelization and comparison of Norton-Hoff and Arrhenius constitutive laws to predict hot tensile behavior of Ti-6Al-4V alloy [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 457-464.
[35] CHEN G, REN C, QIN X, LI J. Temperature dependent work hardening in Ti-6Al-4V alloy over large temperature and strain rate ranges: Experiments and constitutive modeling [J]. Materials & Design, 2015, 83: 598-610.
[36] WEI G B, PENG X D, HU F P, HADADZADEH A, YANG Y, XIE W D, WELLS M A. Deformation behavior and constitutive model for dual-phase Mg-Li alloy at elevated temperatures [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 508-518.
[37] QIN Chun, YAO Ze-kun, NING Yong-quan, SHI Zhi-feng, GUO Hong-zhen. Hot deformation behavior of TC11/Ti-22Al-25Nb dual-alloy in isothermal compression [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 2195-2205.
[38] BALASUNDAR I, RAGHU T, KASHYAP B P. Modeling the hot working behavior of near-α titanium alloy IMI 834 [J]. Progress in Natural Science: Materials International, 2013, 23: 598-607.
[39] WANJARA P, JAHAZI M, MONAJATI H, YUE S, IMMARIGEON J P. Hot working behavior of near-α alloy IMI834 [J]. Materials Science and Engineering A, 2005, 396: 50-60.
[40] SESHACHARYULU T, MEDEIROS S C, FRAZIER W G, PRASAD Y V R K. Hot working of commercial Ti-6Al-4V with an equiaxed α–β microstructure: Materials modeling considerations [J]. Materials Science and Engineering A, 2000, 284: 184-194.
[41] PORNTADAWIT J, UTHAISANGSUK V, CHOUNGTHONG P. Modeling of flow behavior of Ti-6Al-4V alloy at elevated temperatures [J]. Materials Science and Engineering A, 2014, 599: 212-222.
[42] SARKAR A, CHAKRAVARTTY J K. Hot deformation behavior of Zr-1Nb alloy: Characterization by processing map [J]. Journal of Nuclear Materials, 2013, 440: 136-142.
[43] CHAKRAVARTTY J K, DEY G K, BANERJEE S, PRASAD Y V R K. Dynamic recrystallisation during hot working of Zr-2.5Nb: characterisation using processing maps [J]. Materials Science and Technology, 1996, 12: 705-716.
[44] SAXENA K K, SONKAR S, PANCHOLI V, CHAUDHARI G P, SRIVASTAVA D, DEY G K, JHA S K, SAIBABA N. Hot deformation behavior of Zr-2.5Nb alloy: A comparative study using different materials models [J]. Journal of Alloys and Compounds, 2016, 662: 94-101.
[45] RYAN N D, MCQUEEN H J. Mean pass flow stresses and interpass softening in multistage processing of carbon-, HLSA-, tool- and γ-stainless steels [J]. Journal of Mechanical Working Technology, 1986, 12: 323-349.
[46] ZHANG W F, SHA W, YAN W, WANG W, SHAN Y Y, YANG K. Constitutive modeling, microstructure evolution, and processing map for a nitride-strengthened heat-resistant steel [J]. Journal of Materials Engineering and Performance, 2014, 23: 3042-3050.
[47] BANERJEE S, ROBI P S, SRINIVASAN A, PRAVEEN KUMAR L. High temperature deformation behavior of Al-Cu-Mg alloys micro-alloyed with Sn [J]. Materials Science and Engineering A, 2010, 527: 2498-2503.
[48] McQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322: 43-63.
[49] HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena [M]. 2nd ed. Oxford: Pergamon, 2004.
[50] MIRZADEH H, NAJAFIZADEH A, MOAZENY M. Flow curve analysis of 17-4PH stainless steel under hot compression test [J]. Metallurgical and Materials Transactions A, 2009, 40: 2950-2958.
[51] COX B, KNTSKY V G, LEMAIGNAN C, POLICY V, RITCHIE I G, RUHMANN H, SHISHOV V N. Waterside corrosion of zirconium alloys in nuclear power plants [R]. Vienna, Austria: International Atomic Energy Agency (IAEA), 1998.
[52] BRIOTTET L, JONAS J J, MONTHEILLET F. A mechanical interpretation of the activation energy of high temperature deformation in two phase materials [J]. Acta Materialia, 1996, 44: 1665-1672.
[53] DYMENT F, LIBANATI C M. Self-diffusion of Ti, Zr, and Hf in their hcp phases, and diffusion of Nb95 in hcp Zr [J]. Journal of Materials Science, 1968, 3: 349-359.
[54] RAJPUT S K, DIKOVITS M, CHAUDHARI G P, POLETTI C, WARCHOMICKA F, PANCHOLI V, NATH S K. Physical simulation of hot deformation and microstructural evolution of AISI 1016 steel using processing maps [J]. Materials Science and Engineering A, 2013, 587: 291-300.
[55] LANGDON T G. An analysis of flow mechanisms in high temperature creep and superplasticity [J]. Materials Transactions, 2005, 46: 1951-1956.
[56] MUKHERJEE A K. An examination of the constitutive equation for elevated temperature plasticity [J]. Materials Science and Engineering A, 2002, 322: 1-22.
[57] MIRZADEH H. Constitutive analysis of Mg-Al-Zn magnesium alloys during hot deformation [J]. Mechanics of Materials, 2014, 77: 80-85.
[58] MIRZADEH H. Constitutive behaviors of magnesium and Mg-Zn-Zr alloy during hot deformation [J]. Materials Chemistry and Physics, 2015, 152: 123-126.
[59] SAADATKIA S, MIRZADEH H, CABRERA J M. Hot deformation behavior, dynamic recrystallization, and physically-based constitutive modeling of plain carbon steels [J]. Materials Science and Engineering A, 2015, 636: 196-202.
[60] MIRZADEH H. Quantification of the strengthening effect of reinforcements during hot deformation of aluminum-based composites [J]. Materials & Design, 2015, 65: 80-82.
[61] MIRZADEH H. Simple physically-based constitutive equations for hot deformation of 2024 and 7075 aluminum alloys [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 1614-1618.
[62] ZHANG P, HU C, ZHU Q, DING C G, QIN H Y. Hot compression deformation and constitutive modeling of GH4698 alloy [J]. Materials & Design, 2015, 65: 1153-1160.
[63] CAI J, WANG K, MIAO C, LI W, WANG W, YANG J. Constitutive analysis to predict high-temperature flow behavior of BFe10-1-2 cupronickel alloy in consideration of strain [J]. Materials & Design, 2015, 65: 272-279.
[64] ZHAO J, DING H, ZHAO W, HUANG M, WEI D, JIANG Z. Modelling of the hot deformation behaviour of a titanium alloy using constitutive equations and artificial neural network [J]. Computational Materials Science, 2014, 92: 47-56.
[65] ROKNI M R, ZAREI-HANZAKI A, WIDENER C A, CHANGIZIAN P. The strain-compensated constitutive equation for high temperature flow behavior of an Al-Zn-Mg-Cu alloy [J]. Journal of Materials Engineering and Performance, 2014, 23: 4002-4009.
K. K. SAXENA1,4, S. K. JHA2, V. PANCHOLI1, G. P. CHAUDHARI1, D. SRIVASTAVA3, G. K. DEY3, N. SAIBABA2
1. Department of Metallurgical and Materials Engineering, Indian Institute of Technology, Roorkee-247667, Uttarakhand, India;
2. Nuclear Fuel Complex Limited, Hyderabad-501301, India;
3. Materials Science Division, Bhabha Atomic Research Center, Mumbai-40085, India;
4. Department of Mechanical Engineering, Insitute of Engineering and Technology, GLA Uinversity, Mathura-281406, Uttar Pradesh, India
摘 要:通过计算Zr-2.5Nb-0.5Cu合金两相区各相激活能,研究该合金在热变形过程中的主要存在相。在温度为700~925 °C、应变速率为10-2~10-3 s-1的条件下对Zr-2.5Nb-0.5Cu合金进行热机械压缩实验。单相流动应力推广用于两相区各相流动应力的计算,然后利用所得两相区流动应力数据来计算各相的激活能。对计算所得激活能数据进行比较可知,α相为两相区的主要相(形变控制相)。根据形变温度范围或各相存在形式,采用正弦双曲线型本构方程建立了合金的本构方程。统计学分析结果表明,从相关系数(R)和平均相对误差(AARE)考虑,采用为某特定相建立的本构方程所得计算结果与实验结果相符。
关键词:Zr-2.5Nb-0.5Cu合金;热变形;激活能;本构方程;两相材料
(Edited by Wei-ping CHEN)
Corresponding author: K. K. SAXENA; E-mail: saxena0081@gmail.com
DOI: 10.1016/S1003-6326(17)60020-7

