J. Cent. South Univ. (2018) 25: 1418-1436

DOI: https://doi.org/10.1007/s11771-018-3837-1

Novel consistency control strategy for jet dispensing

SHEN Ping(沈平), LI Han-xiong(李涵雄)

State Key Laboratory of High Performance Complex Manufacturing (Central South University),Changsha 410083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: A new consistency control method for jet dispensing is proposed. First, the working parameters, namely, viscosity, supply pressure and supply time, are experimentally investigated. Then, the glue viscosity is approximated by a polynomial model using the least square method. Based on this model and temperature control implemented using the Dahlin principle, the viscosity of the glue can be maintained at a constant value. Then, the viscosity model of the glue is applied to deriving the droplet mass as the nominal model of the temperature controller. The robustness of the temperature controller is analyzed by applying the small gain theory. The glue supply pressure controller is designed using the consistency control strategy, and the robustness is analyzed. Finally, simulations and experiments are conducted using a jet dispensing control system. The results show that the proposed control strategy can significantly improve the droplet consistency.

Key words: jet dispensing; consistency control; internal model control; disturbance rejection; jetting valve

Cite this article as: SHEN Ping, LI Han-xiong. Novel consistency control strategy for jet dispensing [J]. Journal of Central South University, 2018, 25(6): 1418–1436. DOI: https://doi.org/10.1007/s11771-018-3837-1.

1 Introduction

In the electronic manufacturing industry, fluid dispensing has been widely used in various packaging processes, such as advanced integrated circuit encapsulation and surface mount technology [1]. It is one of the key technologies in advanced electronic manufacture [2, 3]. To meet increasing industry requirements, such as high viscosity, tiny droplet, and high frequency, jet dispenser has been widely considered as the next generation of dispensing technology [4]. However, the droplet consistency cannot always be guaranteed in some applications such as LED packaging. One of the key reasons is that the viscosity of glue increases with time such that droplets become smaller, and may finally fail to spray. The droplet volume is affected by different factors, such as temperature and glue supply pressure. A challenge in the dispensing process is the inability to achieve online feedback [5] because the droplet is very small and the working frequency is quite high. Presently, an appropriate sensor that can obtain the precise volume of the glue drop is lacking. Therefore, it is difficult to design an analytical feedback control system.

Presently, existing studies on consistency control are few. Several methods have been designed for contact dispensing. A model-based control for contact dispensing achieved satisfactory droplet consistency [2]. An analytical model that can be adjusted based on the real output of the plant was implemented for a real plant to achieve online feedback. Another model-based control was proposed in Refs. [6, 7] in which methods were developed based on the internal model principle, and software feedback was used to complete the feedback loop. These methods are suitable for contact dispensing, but they may not achieve satisfactory consistency control efficiency for new jet dispensing technology. A strategy was proposed to integrate design and control to improve dispensing consistency [8]. A model-based open-loop control for dielectrophoretic liquid dispensing was reported to have achieved satisfactory droplet volume [9]. Liquid modeling methods and pressure feedback have also been applied in dispensing control [10]. Jet dispensing is a new technology for high-speed and micro-droplet [11]. The above studies achieved jetting consistency; however, they could not solve the jetting consistency problem directly.

Many studies have been conducted based on this technology to improve equipment performance. The breakup behavior of silicone in jet dispensing was studied [12, 13], which is important for jetting valve design. A dynamic model was developed to describe the glue fluid process in the valve [14]. SHAN et al [15] proposed a laminar flow model for the jet dispensing process. WANG et al [16] conducted experimental studies of the jet dispensing process to determine the qualitative features of this process. It is helpful for the following theory studies. The high performance of the valve is very important for droplet consistency, which can reduce random disturbance. A new piezostack actuator was applied to jetting valve to increase the jetting frequency [16–18]. The dynamics of the jet dispenser driven by piezostack was analyzed [19] to demonstrate the use of the analytical method to control a piezostack actuator. An unsteady laminar flow model of the dispensing process was proposed [20] and a clear description of laminar flow in the flow channel was presented. The coupling relationships among viscosity, stroke length, and pulse width have been investigated through experiments [21]. Based on these studies, the mechanism of glue dispensing technology was clarified.

The batch consistency of droplets is mainly affected by the viscosity of glue, which can be considered as a type of disturbance to the control system. A disturbance compensation strategy was implemented [22] to actively compensate for the effects of the varying viscosity of glue. Over the years, several disturbance rejection controls have been proposed [23–28] and many problems have been solved in the industry. Although most of these control methods are based on feedback control, the jetting process can hardly obtain a direct feedback signal. As a result, these disturbance rejection control methods may not be directly applied to the jetting process.

A novel disturbance rejection control for droplet consistency is proposed in this work. First, the coupling relationships are analyzed and a rejection control strategy without online feedback is proposed, which includes a temperature control loop and an internal model-based control for droplet consistency. Then, a nominal model of the jetting process is implemented, which includes a viscosity model and a jetting model. Then, the controller is designed based on the nominal model. Finally, simulation and experimental results are presented to verify the efficiency of the proposed control strategy.

2 Problem formula

The jetting valve is shown in Figure 1. The compressor supplies air pressure at 1–2 MPa against the spring force to lift the needle. At the same time, the glue supply pressure actuates the glue into the cavity. Then, the glue is heated in the cavity, and finally, the air pressure is reduced. The spring drives the needle down to jet the glue out of the nozzle. In this process, the viscosity of the glue increases with time, thereby decreasing the size of the glue droplets.

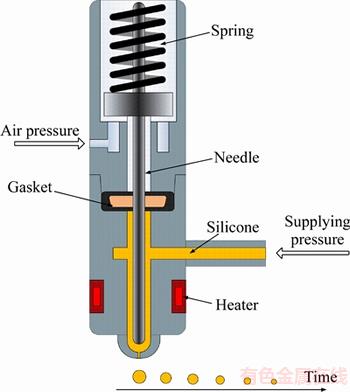
Figure 1 Basic structure of jetting valve

The complex relationship of the coupling parameters is shown in Figure 2. Many parameters can affect the droplet weight, such as the temperature, supply pressure, supply time, and design parameters. Usually, the supply time, temperature, and supply pressure can be controlled by the controller to adjust the droplet mass. However, the droplet weight is very sensitive to the supply time; even an error of 1 ms will result in a large change in the droplet weight. Therefore, the temperature and supply pressure were set as the control signals, while the supply time was set as a constant value.

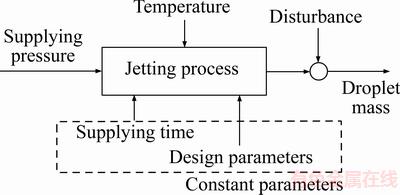
Figure 2 Coupling relationship of the parameters

Most of the conventional control methods are based on online feedback signal. However, online feedback is difficult to achieve in the jetting process because the fluid droplet is very small (<150 nL) and the working frequency is very high. As a result, most conventional control methods cannot be directly applied to this process.

3 Influence of working parameters

To develop an efficiency control system and improve the consistency of the jetting process, the influence of some important working parameters should be investigated. The principles of the working parameters are the basis for modeling and control. In this study, some key parameters were experimentally investigated. Several sensitive parameters were determined and applied to implementing modeling and control.

A high-speed camera was used to record the process of jetting as shown in Figure 3. The jetting process shows jetting out, drawing, and springback subprocesses. First, the fluid is pushed out of the valve, and reaches the bottom. Then, the glue forms silk and eventually breaks. Finally, some glue sticks to the valve and initiates springback. The glue reaching the bottom forms a droplet with a round outline. If the structure does not change, the volume of the droplet is determined by the temperature of the valve, glue supply pressure, glue supply time, initial tension of the spring, and so on.

Figure 3 Jetting process

3.1 Influence of temperature (viscosity)

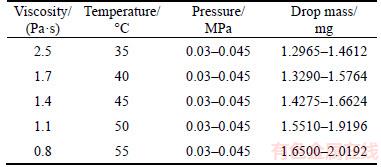
The temperature determines the viscosity of the glue, which affects the volume of the jetting droplet. In this experiment, silicone OE6650 was used to investigate this feature. The testing valve used was AXXON-V6000 and the initial tension was set as 120 N. The route of the needle was 1 mm and the diameter of the nozzle was 0.5 mm. The testing temperature was increased from 35 °C to 55 °C in steps of 5 °C. Every 50 drops are used for testing the volume by the high precise libra.

The experiments were conducted and were separated into four groups with different glue supply pressure in the range of 0.03–0.45 MPa. The experimental results are presented in Table 1.

Table 1 Main parameter settings for temperature experiment

In general, the viscosity of glue decreases as the temperature increases. If the viscosity is too high, the resistance of the needle increases, which can result in difficulties in the movement of the needle and possibly disrupt the movement. Furthermore, if the viscosity is too low, the glue can be easily pressed out and adhere around the nozzle, which ensures that the jetting drops will leave the nozzle.

As shown in Figure 4, under normal working condition, if the temperature is high, the glue is easier to be pressed out of the nozzle to form a larger glue drop. In this experiment, the nozzle cannot jet a normal glue drop under 35 °C. The drop volume increases as the temperature increases. In the temperature range of 35–55 °C, the viscosity decreases from 2.5 Pa·s to 0.8 Pa·s, and the mass increases by 27%. A temperature change of 1 °C can result in 3% change in the volume. The relation between the drop mass and temperature is nonlinear. However, the relationship is linear in some short temperature ranges. Another conclusion from this experiment is that the drop mass becomes more sensitive to the glue supply pressure as the temperature increases, as shown in Figure 5.

Figure 4 Glue drops at different temperatures

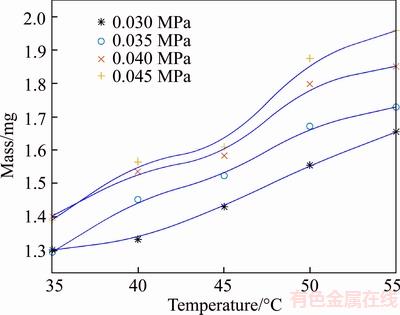
Figure 5 Influence of drop mass at different temperature

3.2 Influence of glue supply pressure

The glue supply pressure is another key parameter of the jetting process. The supply pressure has two effects: it presses the glue to the valve in the supply time and it maintains pressure in the valve, which supplies power for the jetting process. If the supply pressure is too low, the force on the glue may be too low, which makes jetting difficult. In the worst condition, glue supply can be cut off, which creates cavities in the valve and disrupts the jetting process. However, if the supply pressure is too high, it can cause the glue to be pressed out quickly and adhere to the nozzle. It can also disrupt the jetting process.

The influence of the supply pressure was investigated as presented in this section. Silicone OE6650 was used for the experiments. Other parameters were maintained the same as in the previous experiments described earlier. As shown in Figure 6, the supply pressure increases from 0.03 to 0.09 MPa. Every 50 drops are tested by the libra for studying. Five groups of experiments were conducted by setting the supply pressure to 0.03, 0.042, 0.06, 0.072 and 0.09 MPa. The parameter settings are presented in Table 2.

Table 2 Main parameter settings for supply pressure study

In general, the higher the supply pressure, the higher the power for glue jetting and the larger the glue drops. However, if the supply pressure is too high, it will result in increased resistance to the needle movement, and press the glue out of the nozzle within the glue supply time. This will eventually disrupt the jetting process. Furthermore, if the supply pressure is too low, it can result in insufficient glue supply, which can also disrupt the jetting process.

In this experiment, the system cannot operate normally when the supply pressure is lower than 0.02 MPa. Under this condition, some glue drops cannot be jetted out. If the supply pressure is higher than 0.09 MPa, the consistency of the drops will obviously decrease. If the supply pressure continues to increase, the glue will adhere to the nozzle and the jetting process cannot continue.

The experimental results are shown in Figure 7 for the pressure range of 0.03–0.09 MPa. The drop mass increases as the supply pressure increases. The drop mass is very sensitive to the supply pressure. A change of 0.01 MPa in the supply pressure can result in 20% change in the drop mass. As a result, the supply pressure is very important for consistency control. The coupling relation is clearly illustrated in Figure 7. The curve can be uplifted for higher temperatures.

Figure 6 Influence of glue supply pressure

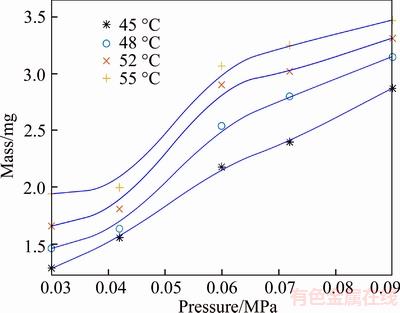
Figure 7 Influence of glue supply pressure

Finally, the consistency control process needs to keep the system in a satisfied condition (0.03–0.09 MPa for this system). The temperature and other coupled parameters should also be considered simultaneously.

3.3 Influence of glue supply time

The glue supply time is also an important parameter that affects the glue drop mass. The glue supply time is the time for glue supply in the valve. To study this parameter, 6 groups of experiments were designed, similar to experiments presented in previous sections. Different time volumes were set as 5, 10, 20, 40, 50 and 60 ms. The main parameter settings are listed in Table 3.

The experimental results are shown in Figure 8. When the supply time is shorter than 5 ms, the valve cannot jet the glue out every time. When the period is longer than 40 ms, the glue will adhere to the nozzle, and the process will be disrupted. When the system operates at a supply time range of 5–40 ms, the glue drops increase with the supply time.

Table 3 Main parameter settings for supply time experiment

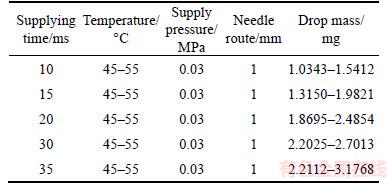
Figure 8 Influence of glue supply time

As shown in this experimental result, the supply time is very sensitive to the drop mass. When the supply time is in the range of 10–30 ms, the drop mass increases with time. The curve shows some saturation features.

However, this result is different from results obtained in previous experiments. The temperature and supply pressure have sufficient resolution ratios to control. The controller is easy to change for 0.2 °C or 0.01 MPa. However, it is difficult for an industry computer to control a valve for 1 ms; therefore, it is also difficult to control the drop mass using the supply time.

However, results from this experiment show that a suitable supply time range can be obtained. This parameter can be fixed in the consistency control process.

4 Proposed consistency control

The failure of direct feedback makes the control process very difficult. In this work, a composite control strategy is proposed as shown in Figure 9, which includes two parts, namely, temperature control and glue supply pressure control.

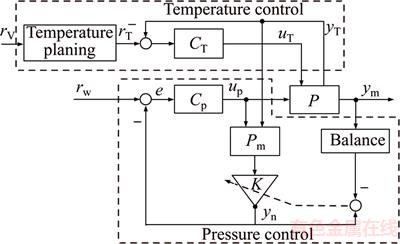
Figure 9 Consistency control strategy

Temperature control is feedback control with temperature planning. Temperature planning can provide a temperature reference volume which can maintain stable viscosity of the glue. In the figure, C_T is the temperature controller, P is the jetting process, r_V is the viscosity reference signal, r_T is the temperature reference signal, u_T is the temperature control signal, and y_T is the temperature output. C_T is used to change the glue temperature to compensate for changes in the glue viscosity so that the viscosity of the glue can be maintained at a stable level.

Pressure control is based on the internal model principle. In Figure 9, C_p is the controller, P_m is the nominal model of P, F is a low-pass filter, K is a tuning parameter, r_w is the drop mass reference signal, e is the error signal, u_p is the supply pressure control signal, and the output y_p is the mass of the droplet. The droplets are weighed every several minutes using high-precision balance. The average weight of the droplets can be obtained and compared with the output of P_m; the result is used to adjust K to make the output of P_m close to the output of P. The output of the nominal model is adjusted through intermittent measurement using the high-precision balance to adopt the real output. Then, the control system can operate under software feedback.

The following section presents details of the temperature control and glue supply pressure control.

4.1 Temperature control

4.1.1 Temperature planning

The viscosity η is affected by the time t and the temperature T with different laws depending on the type of glue. The viscosity increases with time. Furthermore, the temperature T increases as the viscosity decreases, but the solidification time decreases. However, the relationship is very complex and nonlinear. A polynomial model can be applied to describe the relationship of t, T and η. Results of the experiments indicate that a 4th-order polynomial is suitable for the viscosity model.

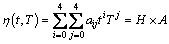                (1)

where

   (2)

In Eq. (1), t is the time, T is the temperature, η is the viscosity, and A is the scale factor.Equation (1) is a linear form for A and A can be identified using the least square method [27]. In this study, the epikote Ausbond 150 T was used as an example. The viscosity data were obtained from the rheometer experiment. The glue was prepared at 25 °C and the variation of the viscosity of the glue with time is shown in Figure 10.

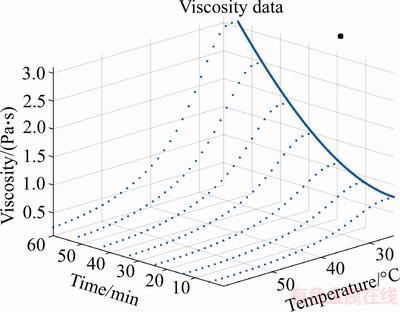
Figure 10 Viscosity data from rheometer experiment

The epikote was modeled in this work using the least square method. The outputs of the models are shown in Figure 11. As seen, the viscosity increases obviously with reducing temperature and increasing time.

The model outputs can approximate the real viscosities. Some contour lines can be drawn as shown in Figure 12. Every contour line represents a stable viscosity of the glue. If temperature control can be implemented to restrict the temperature along one contour line, the viscosity can be maintained.

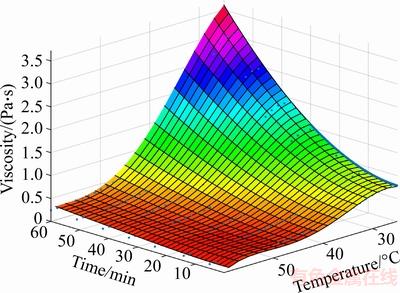
Figure 11 Viscosity model

Figure 12 Viscosity contour lines

4.1.2 Temperature control

The temperature process is usually regarded as a first order plus dead time (FOPDT) process.

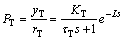                      (3)

where K_T is the stable gain, τ_T is the time constant, and L is the delay time.

The Smith predictor [30] and Dahlin control [31] are efficient control methods for the time-delay process. The Smith predictor has a more complex structure than the Dahlin method. The Dahlin control was selected for temperature control because consistency control is already more complex than the conventional feedback control. The control structure is shown in Figure 13.

The desired system response is designed as given in Eq.(4).

Figure 13 Temperature control structure

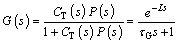               (4)

Using Eq. (4), C_T(s) can be obtained as:

                  (5)

C_T(s) is actually the control law applied with the structure in Figure 14.

As shown in Figure 14, the controller may not be stable for the differential item in the feedback loop. The controller can be improved by adding an inertial item to stabilize it, as shown in Figure 15. Select τ_△<<τ_P to reduce the effects of the inertial item.

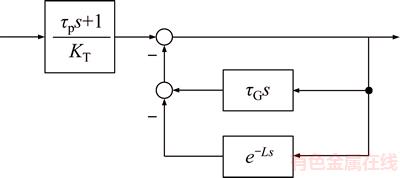
Figure 14 Basic Dahlin control for jetting temperature

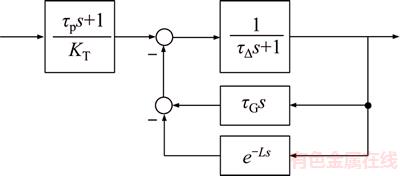
Figure 15 Improved Dahlin control for jetting temperature

Therefore, the controller for the jetting temperature becomes

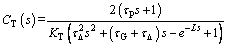        (6)

4.1.3 Robust analysis for temperature control

The robust analysis for temperature control is based on the small gain theory [32]. Suppose an uncertainty exists 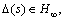and P(s)(1+△)= P_m(s)e^–Ls. Then, the control system is equivalent to Figure 16.

In Figure 16, the transfer function from v_△ to u△ can be described as:

                    (7)

By substituting the parameters into Eq. (7), we obtain:

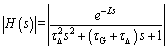                (8)

Let s=jω, Eq. (8) becomes:

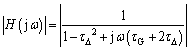             (9)

Equation (9) can be simplified as:

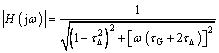        (10)

Based on the small gain theory, the robustness condition can be described as:

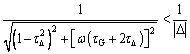            (11)

Based on the stability condition, the modeling error can be measured; the system will be stable if τ_G and τ_Δ can satisfy Eq. (11).

A larger value of

indicates higher robustness; τ_G is the response speed of the system. A suitable value of τ_G and τ_Δ should be set to ensure appropriate balance between robustness and response speed.

Figure 16 Robust analysis for temperature control

4.2 Glue supply pressure controller design

4.2.1 Droplet volume model

The nominal model is very important for consistency control and it is derived in this section. The nominal model is divided into two parts as shown in Figure 17. The viscosity model was derived in Section 2.1. The droplet mass is derived in this section. Droplets are caused by the pressure of the needle and needle movement. Details of these two parts are presented as follows.

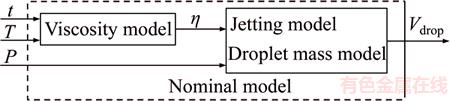
Figure 17 Nominal model structure

1) Droplet volume by needle pressure

Fluid in the jetting valve can be modeled as shown in Figure 18. Under the pressure of the needle, fluid flows in two directions: downward flow and backward flow. The fluid flowing downward will flow out of the valve and form a droplet. The fluid flowing backward will flow along the supply path. The parameters for the jetting model are listed in Table 4.

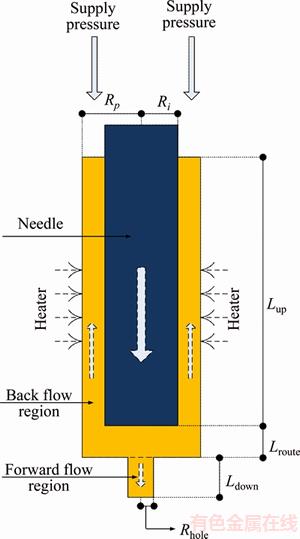
Figure 18 Fluid division

The purpose of the jetting model is to develop the relationship among the supply pressure, viscosity, and the drop mass. If the drop mass model is analyzed directly, the error may be significant since the characteristics of the glue is too complex to be expressed using mathematical equations. However, the volume occupied by the needle moving V_drain can be calculated accurately.

Table 4 Parameters for nominal model

This portion of the fluid is divided into two parts. One part is the fluid flowing back to the back flow region against the supply pressure, while the other part is flowing to the forward flow region and is jetted out of the valve.

The process for one droplet is very short (less than 2 ms), and measurement equipment cannot operate accurately in such a short time. Thus, the process for one drop is considered as a constant process. The droplet volume can be approximated as follows:

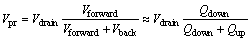    (12)

Flow quantity of back flow region:

The annular pipe flow is approximated to a parallel plate flow process for a simpler analytical result since the gap between the needle and the lining is far less than the needle radius. In this case, laminar flow between parallel plates is symmetrical. The flow velocity and the quantity of flow are symmetrical by the center parting plane. Therefore, only half of the region is modeled.

Based on the above approximation, the shear stress on the center plane is 0. Then,

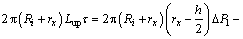
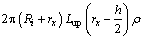                (13)

Based on Eq. (13), the shear stress can be expressed as:

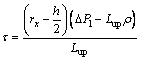                   (14)

Consider the general power-law flow:

                             (15)

The shear stress distribution of the annular back flow region can be obtained by applying Eq. (15), as shown in Figure 19.

Figure 19 Shear stress and velocity in gap

The shearing rate can be expressed as:

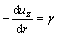                              (16)

Quantity of flow for region τ>τ_y

Based on Eqs. (15) and (16), we obtain:

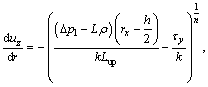
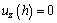(17)

Then, the flow velocity can be expressed as:

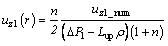               (18)

with

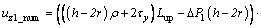
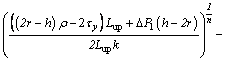
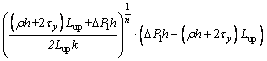(19)

The flow quantity of the back flow region can be expressed as:

                          (20)

Based on Eq. (20), the factor for τ=τ_y is obtained as:

                    (21)

where ah is a plane where τ=τ_y.

The solution of Eq. (20) is the flow quantity of the back flow region for τ>τ_y.

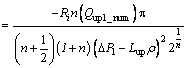          (22)

with

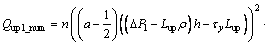
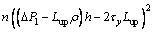              (23)

Quantity of flow for region τ<τ_y, when τ<τ_y, the shear rate γ=0. Then, the liquid flow can be regarded as a rigid body movement. Equation (24) can be obtained through a similar process.

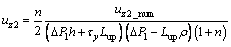      (24)

with

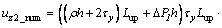
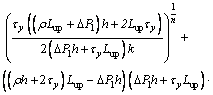
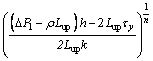              (25)

The flow quantity can be obtained as:

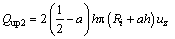
(26)

with

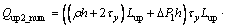
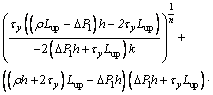
               (27)

Using Eqs. (24) and (26), the quantity of the back flow region can be obtained as:

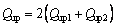                      (28)

In reality, Eq. (28) is too complex to design the controller. In the real jetting process, high quantity of glue can be regarded as power-law fluid. For power-law fluid, τ_y=0, and the quantity of the back flow is simplified as:

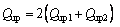
(29)

Under certain conditions, the glue can be regarded as Newtonian fluid with n=1; the quantity of the back flow can be obtained as:

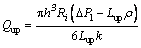                   (30)

Flow quantity of jetting region:

Based on the equilibrium of the micro pipe, we obtain:

                        (31)

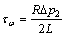                             (32)

The shear stress can be expressed as:

                              (33)

The shear rate is given as:

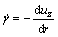                              (34)

Using the relationship between the shear rate and the shear stress 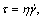 the flow velocity can be deduced as:

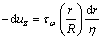                        (35)

For the general power-law fluid, we have:

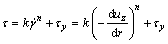               (36)

The radius for τ=τ_y is given as:

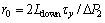                        (37)

Then, the solution of Eq. (35) is the velocity of this region.

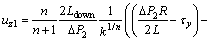
                     (38)

Similarly, the velocity for τ<τ_y can be expressed as:

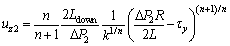       (39)

Based on Eqs. (38) and (39), the quantity of the jetting region can be derived as:

(40)

with

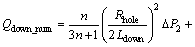
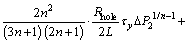
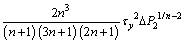          (41)

For the power-law, τ_y=0, Q_down can be simplified as:

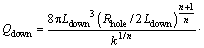
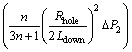                 (42)

When the fluid is Newtonian fluid, n=1, Q_down can be simplified again as:

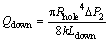                       (43)

Then the droplet volume due to the needle pressure can be deduced from Eq. (7).

2) Flow quantity by the movement of needle:

In the jetting process, needle movement results in some flow quantity for adhesion between the needle and glue. Similarly, it is approximated as flow between parallel plates. Under the effect of shear stress, the flow velocity is shown in Figure 20.

The velocity distribution [33] is given as:

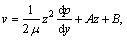
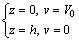          (44)

where V₀ is the velocity of the needle, and v is the velocity of the glue. From Eq. (44), we obtain:

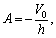
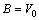                         (45)

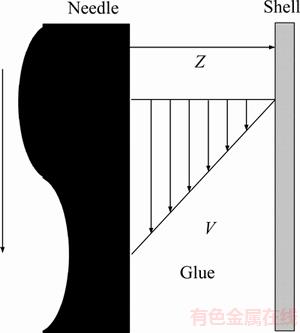
Figure 20 Velocity due to movement of needle

Then, the velocity can be deduced as:

                            (46)

where z is the distance to the needle surface, and h is the distance between the needle and shell. Therefore, we obtain:

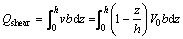             (47)

where b is the perimeter of the needle. That is,

                           (48)

Thus, the droplet volume due to shear stress can be described as:

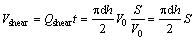            (49)

The total droplet volume can be obtained as:

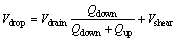              (50)

Most of the glue in the jetting process can be described as power-law fluid, so that τ_y=0. Thus,

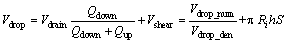(51)

with

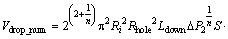
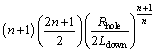              (52)

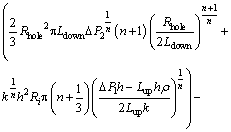
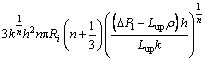       (53)

Some glue in the jetting process can be described as Newtonian fluid, so that n=1. Thus,

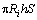                             (54)

Finally, the mass of the droplet can be estimated as:

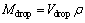                          (55)

4.2.2 Glue supply pressure control

In the controller design, the droplet volume model based on Newtonian fluid is used to improve the applicability of the controller.

To design a suitable controller, the equivalent model shown in Figure 21 can be used. An additional item G₁ is combined with the jet dispensing process G_N. The two models form a linear model, which is easier to apply in the design of the controller.

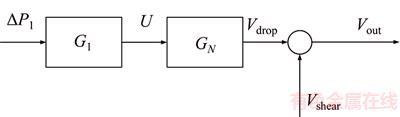
Figure 21 Equivalent model for controller design

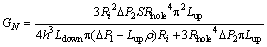  (56)

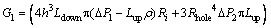 (57)

Based on Eq. (57), the differential pressure between the needle bottom pressure and supply pressure ΔP₁ can be derived as:

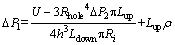              (58)

Then, the glue supply pressure is obtained as:

      (59)

In the jetting process, the supply pressure is adjusted by the pressure regulating valve. The model of the valve is given in Eq. (60), where K_v is the stable gain and T_v is the time constant.

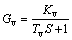                            (60)

Suppose the entire system is an ideal model, that is:

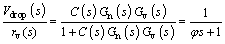       (61)

Based on Eq. (61), the controller C(s) can be described as:

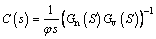                (62)

where φ is a parameter that ensures a trade-off between robustness and response. Based on Eqs. (61) and (62), the controller can be described as:

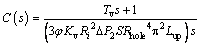           (63)

It is clear that the controller is a PI-type controller. The scale factor is given as:

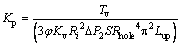             (64)

The integrating factor is:

             (65)

From the parameters in Eqs. (63)–(65), the controller is a nonlinear time-varying type controller, as shown in Figure 22.

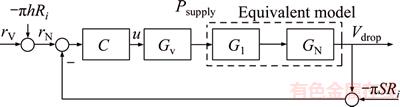
Figure 22 Control structure of jetting process

4.2.3 Robustness analysis for pressure control

Similar to the temperature control based on the small gain theory [32], it is assumed that an uncertainty exists 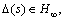and P(s)(1+Δ)= P_m(s)e^–LS. Then, the control system is equivalent to the system shown in Figure 23.

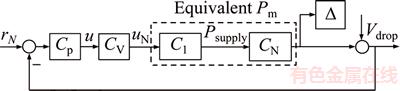
Figure 23 Control structure of jetting process

In the system shown in Figure 23, the transfer function from v_Δ to u_Δ is:

              (66)

By substituting all the parameters into Eq. (66), we obtain:

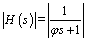                          (67)

Let s=jω, then Eq. (67) becomes:

                     (68)

The robustness stability condition can be obtained using the small gain theory as:

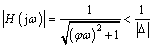                 (69)

Set a suitable volume of φ to satisfy Eq. (69) and ensure the stability of the entire system. A larger value of φ indicates higher robustness and lower response speed. Therefore, a tradeoff is necessary.

5 Simulation and experiment

5.1 Consistency control simulation

Three simulations were carried out as presented in this section. The first and second simulations are temperature control and supply pressure control without model mismatch, while model mismatch is considered in the third simulation. White noise disturbance exists in all the three simulations.

The conditions are set as follows: environment temperature was set as 25 °C, the nozzle of the jetting valve was heated under the controller, and the glue supply pressure controller was set as 0.03 MPa.

If the nominal model can accurately match the jetting process, the output of the plant will be the same as that of the nominal model. The control response is shown in Figures 24 and 25. As the viscosity of the glue increases, the droplet volume decreases by approximately 16% if there is no control.

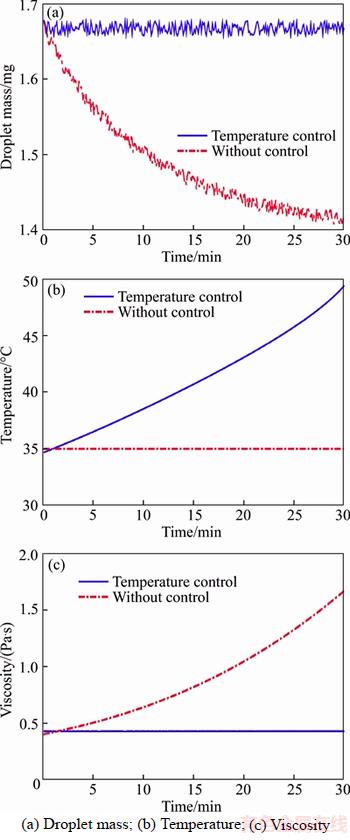
Figure 24 Consistency control under ideal condition (temperature control):

In the temperature control simulation, the viscosity is maintained at 0.8 Pa·s. After 30 min, the temperature of the nozzle increases from approximately 35 to 49 °C. The drop mass can be controlled at approximately 1.67 mg as shown in Figure 24.

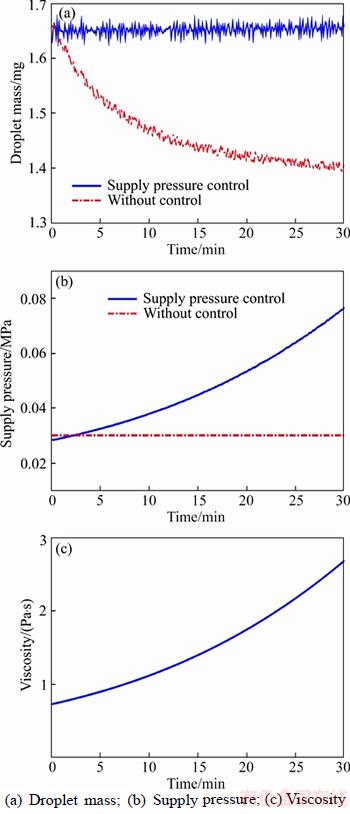
Figure 25 Consistency control under ideal condition (supply pressure control):

The second simulation investigates the performance of the supply pressure control as shown in Figure 25. The temperature was maintained at 35 °C. It indicates that after 30 min, the viscosity increases significantly. The epikote viscosity increases from 0.8 to 2.7 Pa·s. With the controller in Eq. (61), the supply pressure increases from 0.03 to 0.076 MPa. The controller can also maintain the droplet mass at approximately g.

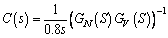               (70)

In the third simulation, the jetting process is assumed to have model mismatch and random output disturbance. For instance, the radius of the needle is smaller than that of the nominal model. The back flow of the plant will be larger than that of the nominal model. As a result, the output of the plant will be smaller than that of the nominal model, which can result in a control error. The adjusting parameter K is tuned every 5 min. However, the error can be compensated by applying the proposed control strategy as shown in Figure 26. Because the nominal model does not perfectly match the plant, the output of the plant cannot track the reference signal. However, after the parameter K is adjusted once, the output of the plant can be maintained at approximately 1.67 mg.

Figure 26 Consistency control with model error:

5.2 Consistency control experiment

The experimental setup is shown in Figure 27. The hardware control system is based on an industrial computer with Googoltech control card. The structure of the system is shown in Figure 28, all the actuators and sensors are connected to the computer indirectly.

Silicone and epikote are common glues in microelectronics packaging industry. The two glue types have very different features. For instance, silicone is more stable. After mixing A and glue B, the viscosity only changes minimally after 1.5 h. However, the features of epikote are quite different from those of silicone. After adding a curing agent, the viscosity of epikote changes significantly after 1.5 h.

Figure 27 Jet dispensing system and control system

If a controller is not used, the jetting mass will be significantly affected. Based on the above description, epikote was selected for testing the proposed control method.

5.2.1 Consistency control without controller

In this experiment, the control system uses constant temperature and glue supply pressure. The temperature was set to 35 °C, and was measured every 5 min. The experimental results are presented in Table 5 and Figure 29.

As presented in Table 5, the mass of the 50 drops decreased from 0.0818 to 0.0498 g or a decrease of 37.75%. This is significantly different from the reference consistency and cannot satisfy the requirement of the microelectronics packaging industry. The proposed method was applied to enhancing jetting consistency as presented below.

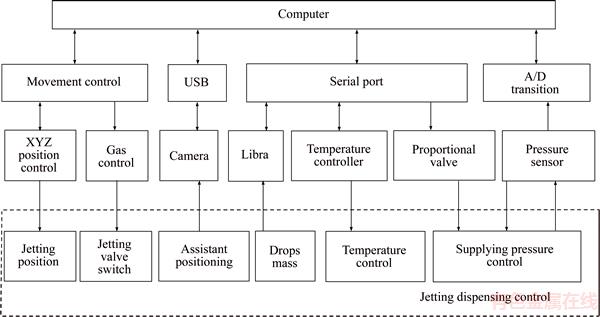
Figure 28 Structure of control system

Table 5 Experimental result without consistency control

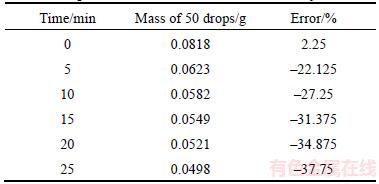
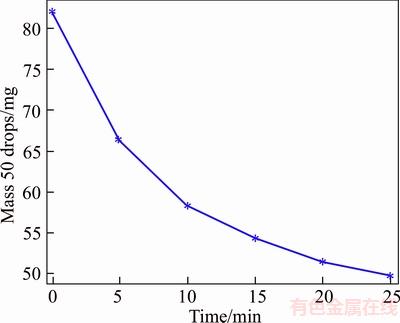
Figure 29 Experimental result without consistency control

5.2.2 Consistency control with temperature regulation

Based on the previous control algorithm, the temperature for maintaining the viscosity can be obtained. Using this volume, the viscosity can be maintained at a constant volume by the temperature controller and the heater around the valve.

Under this condition, the controller performance is shown in Figure 30.

With the temperature control system, the viscosity of silicone is maintained at approximately 1.1 Pa·s. The temperature of the valve increases from 36 to approximately 50 °C. The glue supply pressure was set as 0.03 MPa. The drops mass (50 drops) can be adjusted to within 0.78–0.85 g. The consistency is 4.5% and the largest error compared to the reference signal is 6.3%, as listed in Table 6.

Figure 30 Performance of temperature control:

It is obvious that temperature control can increase the consistency of jet dispensing, as shown in Figure 31. For epikote, the consistency is significantly lower than 10% without control, but it can be improved to 10% using temperature control. This indicates a satisfactory result.

Considering the control process, the temperature increases to 50 °C. This represents a high volume for this system, which may lead to fast solidification of the glue. Furthermore, the modeling error of the glue is very sensitive to the experimental result. To solve these two problems, the combined use of temperature and pressure is necessary to maintain consistency.

Table 6 Parameter settings for temperature control

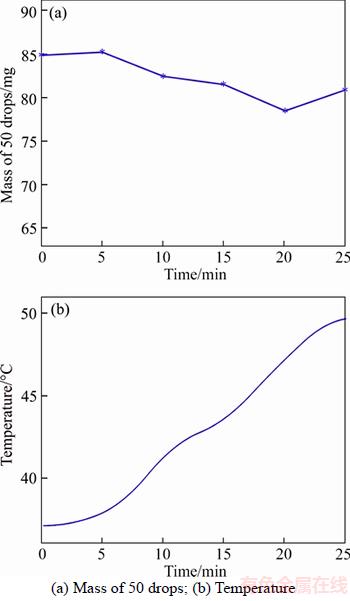
Figure 31 Consistency control by temperature regulation:

5.2.3 Consistency control with temperature and pressure regulation

In the consistency control experiment, epikote with high viscosity was sprayed out of the valve. The viscosity reference was set as 0.8 Pa·s, and the desired temperature can be obtained as shown in Figure 32. The temperature controller is designed as:

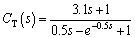                    (71)

Figure 32 Consistency control experiment:

Then the control strategy is compiled using Qt platform. The control parameters were selected as the same as in the simulations, as listed in Table 7. The temperature was controlled along the 0.8 Pa·s contour line. The glue supply pressure was adjusted under software feedback. The nominal model was adjusted every 5 min. Thus, the supply pressure may include inflexions every 5 min.

Table 7 Parameter settings for multiple control

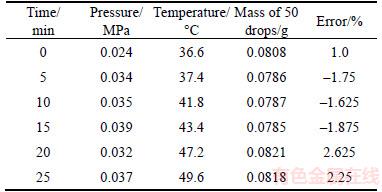
Finally, the experimental results are shown in Figure 32. The mass of 50 drops is maintained as approximately 0.083 g. The consistency is 2.4%, which is significantly better than the performance without consistency control (>15%).

6 Conclusions

The batch consistency control of jet dispensing is disturbed mainly by the viscosity of the glue. Based on the strategy of disturbance rejection control, the batch consistency can be compensated by adjusting the temperature and supply pressure. However, most feedback control cannot be applied directly because online feedback cannot be achieved. A novel consistency control for batch consistency is proposed in this work based on internal model control. The efficiency of the proposed method is verified through simulations and experiments.

References

[1] NGUON B, JOUANEH M. Design and characterization of a precision fluid dispensing valve [J]. The International Journal of Advanced Manufacturing Technology, 2004, 24(3, 4): 251–260.

[2] LI Han-xiong, LI H X, LIU J, CHEN C P, DENG H. A simple model-based approach for fluid dispensing analysis and control [J]. Mechatronics, IEEE/ASME Transactions, 2007, 12(4): 491–503.

[3] KOIDE A, SASAKI Y, YOSHIMURA Y, MIYAKE R, TERAYAMA T. Micromachined dispenser with high flow rate and high resolution in micro electro mechanical systems [C]// The Thirteenth Annual International Conference. 2000: 424–428.

[4] JIA H, HUA Z, LI M, ZHANG J. A jetting system for chip on glass package [C]// International Conference on Electronic Packaging Technology & High Density Packaging. 2009: 954–960.

[5] CHEN X B, ZHANG W J, SCHOENAU G, SURGENOR B. Off-line control of time-pressure dispensing processes for electronics packaging [J]. Electronics Packaging Manufacturing, IEEE Transactions, 2003, 26(4): 286–293.

[6] CHEN X B, SCHOENAU G, ZHANG W J. Modeling and control of dispensing processes for surface mount technology [J]. Mechatronics, IEEE/ASME Transactions, 2005, 10(3): 326–334.

[7] CHEN Cong-ping, LI Han-xiong, DING Han. Modeling and control of time-pressure dispensing for semiconductor manufacturing [J]. International Journal of Automation and Computing, 2007, 4(4): 422–427.

[8] LI Han-xiong, TSO S K, DENG Hua. A conceptual approach to integrate design and control for the epoxy dispensing process [J]. The International Journal of Advanced Manufacturing Technology, 2001, 17(9): 677–682.

[9] WANG K L, JONES T B, RAISANEN A. Dynamic control of DEP actuation and droplet dispensing [J]. Journal of Micromechanics and Microengineering, 2007, 17(1): 76–80.

[10] CHEN D X. Modeling and off-line control of fluid dispensing for electronics packaging [D]. University of Saskatchewan, 2002.

[11] HORATIO Q, BABIARZ A, FANG L. Jetting technology: A way of the future in dispensing [C]// Proceedings of the 4th International Symposium on Electronic Materials and Packaging. 2003: 7–14.

[12] CHEN Yun, WANG Fu-liang, LI Han-xiong. Experimental and modeling study of breakup behavior in silicone jet dispensing for light-emitting diode packaging [J]. IEEE Transactions on Components Packaging & Manufacturing Technology, 2015, 5(7): 1019–1026.

[13] CHEN Y, GAO J , CHEN X, YANG Z, HE Y. Comparison of the break-up behaviors of newton and shear thinning non-newton fluid in jet dispensing for LED packaging [C]// International Conference on Electronic Packaging Technology. 2015: 1029–1032.

[14] DENG Gui-ling, ZHONG Jue. Fluid dynamics models for non-Newtonian fluid transferring mechanism in contact dispensing dot process [J]. Journal of Central South University, 2006, 37(1): 84–90.

[15] SHAN X Y, CHEN Y, PENG X A, LI H X. Modeling of laminar fluid flow in jet dispensing process [C]// International Conference on Electronic Packaging Technology. 2014: 276–279.

[16] WANG L, DU J, LUO Z, DU X, LI Y. Design and experiment of a jetting dispenser driven by piezostack actuator [J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2013, 3(1): 147–156.

[17] LU S Z, LIU Y, YAO Y, SUN L, ZHONG M. Bond-graph model of a piezostack driven jetting dispenser [J]. Simulation Modelling Practice & Theory, 2014, 49: 193–202.

[18] JEON J C, QUOC H N, SEUNG B C. The design and modeling of jetting dispenser actuated by dual piezostack actuator [J]. Applied Mechanics & Materials, 2013, 433–435: 72–75.

[19] NGUYEN Q H, HAN Y M, CHOI S B, HONG S M. Dynamic characteristics of a new jetting dispenser driven by piezostack actuator [J]. IEEE Transactions on Electronics Packaging Manufacturing, 2008, 31(3): 248–259.

[20] NGUYEN Q H, CHOI S B. Modeling of unsteady laminar flow based on steady solution in jetting dispensing process [J]. IEEE Transactions on Electronics Packaging Manufacturing, 2008, 31(2): 134–142.

[21] SHU X Y, ZHANG H H, LIU H Y, XIE D, XIAO J F. Experimental study on high viscosity fluid micro-droplet jetting system [J]. Science in China Series E: Technological Sciences, 2010, 53(1): 182–187.

[22] LI H X, van den BOSCH P P J. A robust disturbance-based control and its application [J]. International Journal of Control, 1993, 58(3): 537–554.

[23] CHEN Wen-hua. Disturbance observer based control for nonlinear systems [J]. IEEE/ASME Transactions on Mechatronics, 2005, 9(4): 706–710.

[24] CHEN Yi-de. Modified smith predictor scheme for periodic disturbance reduction in linear delay systems [J]. Journal of Process Control, 2007, 17(10): 799–804.

[25] SHEN Ping, LI Han-xiong. A multiple periodic disturbance rejection control for process with long dead-time [J]. Journal of Process Control, 2014, 24(9): 1394–1401.

[26] SHEN Ping, LI Han-xiong. The consistency control of mold level in casting process [J]. Control Engineering Practice, 2017, 62: 70–78.

[27] JIN Qi-bing, LIU Li-ye. Design of active disturbance rejection internal model control strategy for SISO system with time delay process [J]. Journal of Central South University, 2015, 22(5): 1725–1736.

[28] FAN S X, FAN D P, HONG H J, ZHANG Z Y. Robust tracking control for micro machine tools with load uncertainties [J]. Journal of Central South University, 2012, 19(1): 117–127.

[29] LJUNG L. System identification, in signal analysis and prediction [M]. Springer, 1998.

[30] LAUGHLIN D, RIVERA D, MANFREDMORARI. Smith predictor design for robust performance [J]. International Journal of Control, 1987, 46(2): 477–504.

[31] DAHLIN E B. Designing and tuning digital controllers [J]. Instruments & Control Systems, 1968, 42: 77–83.

[32] GU Da-wei, PETKOV H R, KONSTANTINOV M M. robust control design with MATLAB [M]. Springer, 2005.

[33] BLEVINS R D. Applied fluid dynamics handbook [M]. New York: Van Nostrand Reinhold Co., 1984.

(Edited by FANG Jing-hua)

中文导读

一种新型喷射式点胶一致性控制方法

摘要：提出一种新的喷射式点胶一致性控制方法。首先，通过实验研究胶液黏度、供胶压力、补胶时间等工作参数的影响规律，并基于最小二乘法建立了胶液黏度的多项式模型。然后基于黏度模型与温度特性，采用Dahlin算法设计了温度控制器，可在一定时间范围内将胶液的黏度维持在恒定的水平。基于胶液的黏度模型，建立了胶滴质量的温度控制系统的名义模型，基于小增益原理分析了温度控制系统的稳定性。而后进一步设计了供胶压力控制器，结合温度控制实现了出胶量的一致性控制。最后通过仿真与实验说明了本控制方法的有效性。

关键词：喷射式点胶；一致性控制；内模控制；扰动抑制；喷射阀

Foundation item: Project(2011CB013104) supported by the National Basic Research Program of China

Received date: 2016-12-29; Accepted date: 2017-04-05

Corresponding author: SHEN Ping, PhD; Tel: +86-13787786033; E-mail: ppguitar1983@sina.com; ORCID: 0000-0002-2794-5464