Trans. Nonferrous Met. Soc. China 22(2012) s859-s863
Thermal deformation of aluminum alloy casting materials for tire mold by numerical analysis
Hee-Sung YOON1, Je-Se CHOI1, Yool-Kwon OH2
1. Department of Advanced Parts and Materials Engineering, Chosun University, Gwangju 501-759, Korea;
2. Department of Mechatronics Engineering, Chosun University, Gwangju 501-759, Korea
Received 21 May 2012; accepted 5 November 2012
Abstract: Thermal deformation of aluminum alloy casting materials for manufacturing the tire mold was numerically investigated. The AC7A and AC4C casting material was selected as casting material and the metal casting device was used in order to manufacture the mold product of automobile tire in the actual industrial field. The temperature distribution and the cooling time of casting materials were numerically calculated by finite element analysis (FEA). Also, the thermal deformation such as displacement and stress distribution was calculated from the temperature results. The thermal deformation was closely related to the temperature difference between the surface and inside of the casting. The numerical analysis results reveal that the thermal deformation of AC7A casting material is higher than that of AC4C casting material. Also, the thermal deformation results at the central part are larger than that on the side of casting because of the shrinkage caused by the cooling speed difference.
Key words: thermal deformation; finite element analysis; AC7A casting material; AC4C casting material
1 Introduction
The precision and endurance of tire mold used in manufacturing process of automobile tire is very important factor to decide the quality of tire. Tread pattern of tire is formed by tire mold and is the important technology of tire as a control system, such as tire braking force, driving performance, noise and vibration. Also, it has directly influenced the inclination of a car body or abrasion of the tire and a tire’s life [1]. So, many industries and researchers associated with tire mold production have studied the production of the mold of good quality and reduction of the manufacturing period. The temperature distribution of the casting and the growth rate of the solidification interface play a very important role in determining fine structure, mechanical and physical properties of the casting material during cooling process of the casting. In order to predict and control the temperature distribution and the growth rate of the solidification interface, it is necessary to accurately understand the heat transfer characteristic at the casting mold interface. In the casting process, it is very important for evaluating the metal structure and quality of the products to know the temperature change by time [2]. So, many researches for this have been reported in the literatures [3-7]. SHEPEL and PADLUCCI [8] investigated filling and solidification of permanent mold casting by numerical simulation. VIJAYARAM et al [9] and HONG et al [10] investigated the numerical simulation of casting solidification in permanent metallic mold. KANG and ZABARAS [11] investigated on control of the freezing interface motion in two-dimensional solidification processes using the adjoint method. RICHMOND and TIEN [12] investigated thermal stress and air gap formation during the early stages of solidification in a rectangular mold. The metal casting method used for manufacturing the mold for automobile tire in the actual industrial was applied because of the precision, the cost reduction and manufacturing time reduction of mold product. So, thermal deformation of aluminum alloy casting materials was numerically investigated for manufacturing the tire mold. Also, in order to verify the results calculated by the numerical analysis, the experiment was carried out using the metal casting device actually used for manufacturing the tire mold.
2 Numerical analysis
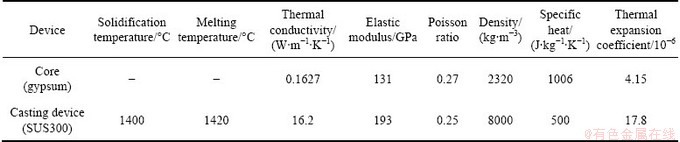
In this study, the metal casting device used of manufacturing the mold for automobile tire was analyzed with analysis model, and the Al-Si-Mg system alloy, AC7A and AC4C, are selected as a casting material. The physical properties of ACTA and AC4C aluminum alloy are listed in Table 1 [13,14]. Physical properties of core and metal casting device are listed in Table 2.
The numerical analysis was performed to predict temperature and thermal deformation such as displacement and stress inside AC7A and AC4C casting materials by finite element analysis (FEA). For the numerical analysis, the commercial program “COMSOL Multiphysics” which can carry out the heat transfer analysis and thermal-structural analysis was used.
Figures 1 and 2 show the 3-dimensional analysis model and temperature measurement locations inside the casting. The analysis model consisted of upper and lower parts of metal casting device, core and casting. The analysis model for heat transfer by conduction is the heat equation:
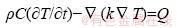(1)
where T is temperature; ρ is density; C is heat capacity; k is thermal conductivity and Q is heat source or heat sink. The boundary condition is given by the metal casting device; the contact surface between the core and casting material was assumed to be in conduction; and the inside of the parts other than the contact surface were assumed to be in convection and heat flux.
n(k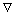
T)=h(Tinf-T)+Cconst(T4amb-T4) (2)
where h is the heat transfer coefficient associated with the free convection; Tinf is the ambient bulk temperature; Tamb is the temperature of the surrounding radiation environment, which might differ from Tinf; Cconst is the product of the surface emissitivity ε and the Stefan- Boltzman constant σ=5.669×10-8 W/(m2·K4):
Cconst=εσ (3)
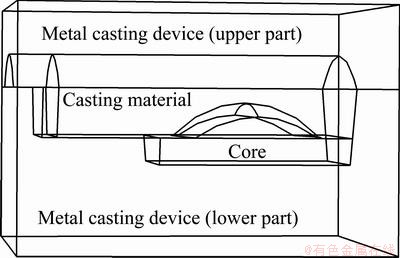
Fig. 1 Schematic diagram of 3-dimensional analysis model
Fig. 2 Schematic diagram of temperature measurement locations inside casting
The initial temperature condition of each part was pre-determined as 300 °C for the metal casting device, 80 °C for the core, 650 °C for AC7A casting material and 620 °C for AC4C casting material, respectively. The numerical analysis was carried out by calculating the temperature inside the casting material for 15 min for AC7A casting material and 25 min for AC4C casting material from initial state based on the finding from the previous researches to improve production time and manufacturing processes, respectively. Here, the initial state means the state in which the casting material was completely injected into the metal casting device. Thermal deformation such as displacement and stress inside the casting material was calculated from temperature results.
Table 1 Physical properties of AC7A and AC4C aluminum alloy
Table 2 Physical properties of core and metal casting device
In order to verify the results calculated by the numerical analysis, the experiment was carried out using the metal casting device actually used for manufacturing the tire mold. The experiment was carried out 3 times under the same condition to get accurate temperature measurement results. The experimental set-up consisted of the casting, the core, the metal casting device, data acquisition unit, K-type thermocouple and PC. The core that determined the tread pattern of tire was installed inside the metal casting device. In order to measure the temperature distribution inside the casting during cooling process, 9 thermocouples were installed on the pre-determined positions above the core surface as shown in Fig. 2. Each thermocouple was sealed with the stainless steel tube for the purpose of device protection and insulation. All thermocouples were connected to the data acquisition unit, and the measured temperature data was automatically recorded on the PC.
In order to minimize the casting deformation by rapid temperature difference during the injection of casting material, the metal casting device and core were preheated at 300 °C and 80 °C, respectively. The AC7A and AC4C ingots were heated in the smelting furnace at 680 °C and 650 °C, and then injected into the metal casting device when the melting process was completely finished.
3 Results and discussion
Figures 3 and 4 show the temperature distribution inside the AC7A and AC4C casting materials calculated by numerical analysis during 15 min and 25 min. The middle part (i.e., locations 4, 5 and 6) temperature inside the casting is higher than that at contact parts of the casting and the metal casting device. The rapid heat transfer occurs on contact parts of the casting and the metal casting device because the metal casting device is in contact with the casting surface. The solidification patterns of two casting materials are similar to that shown in Figs. 3 and 4.
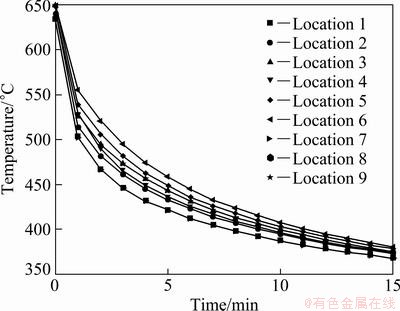
Fig. 3 Temperature distribution inside casting by numerical analysis (AC7A casting material)
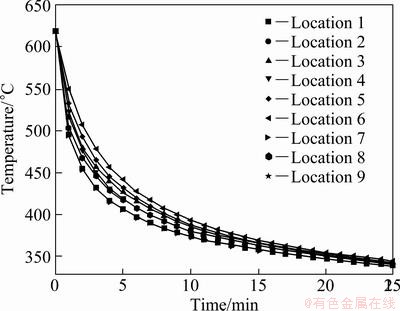
Fig. 4 Temperature distribution inside casting by numerical analysis (AC4C casting material)
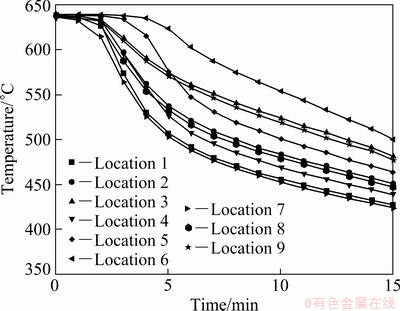
Fig. 5 Temperature distribution inside casting by experiment (AC7A casting material)
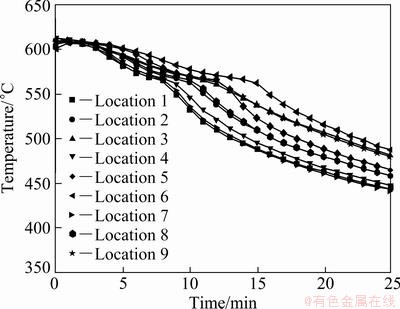
Fig. 6 Temperature distribution inside casting by experiment (AC4C casting material)
Figures 5 and 6 show the experimental results of temperature distribution under the same condition with numerical analysis. Like results of temperature distribution calculated by numerical analysis, the temperature at middle part appears to be higher than that at both sides. The cooling pattern is almost uniformly maintained during the initial solidification process, unlike the results of temperature distribution calculated by numerical analysis method. The temperature distribution of the AC7A and AC4C casting materials are almost uniformly maintained from initial state to about 5 and 12 min due to the phase change process, respectively. Although, there are some temperature differences between experimental and numerical results, the solidification patterns except for phase change process and solidification time are almost similar results, when the experimental results are compared with numerical results.
Figure 7 shows thermal curve interpretation of pure Al alloy and Al-5% Mg alloy. This thermal curve is to measure the temperature change by the cooling time when the liquid material of melting state is completely solidified. The pure aluminum exists as liquid state by point A when the pure aluminum is heated at about 700 °C. After temperature of melted aluminum uniformly decreased to 660 °C, it becomes solidification by point B. At this point, it maintains regular temperature because the cooling is delayed by latent heat of melting. This is explained uniformly solidification pattern during the initial cooling process as shown in Figs. 5 and 6.
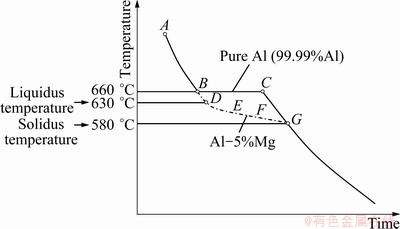
Fig. 7 Thermal curve interpretation of pure Al and Al-5%Mg alloy
Thermal deformation such as displacement and stress was calculated from temperature results. Figures 8 and 9 show the numerical results of displacement distribution in the casting using AC7A and AC4C casting material, respectively. Displacement at the middle part in the casting is larger than that at contact parts of the casting and the metal casting device because the rapid heat transfer occurs on contact parts of the casting and the metal casting device.
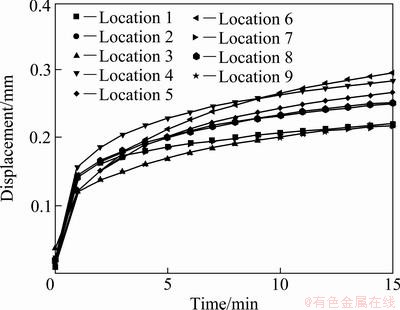
Fig. 8 Displacement distribution inside casting by numerical analysis (AC7A casting material)
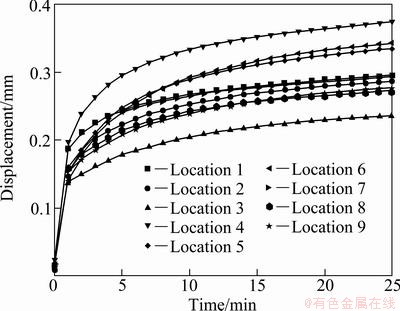
Fig. 9 Displacement distribution inside casting by numerical analysis (AC4C casting material)
According to the displacement results of two casting materials, displacement of AC7A casting material approximately 0.6 mm lowers than that of AC4C casting material one. Displacement of AC7A casting material is reduced by approximately 17%, which is more than AC4C casting material.
Figures 10 and 11 show the numerical result of stress distribution in the casting using AC7A and AC4C casting material, respectively. The solidification time of the middle part in the casting is slower than that of contact parts of the casting and the metal casting device by the flow characteristic of the casting material. Because of the shrinkage caused by the solidification time difference in the casting, the stress distribution is larger at the middle part in the casting. The stress distribution is larger on the location 5 than that on other points by slowly solidification time because it is located to central part of the casting. The stress of AC7A casting material is approximately 0.17 GPa lowers than that of AC4C casting material. From these results, thermal deformation is generated by the temperature difference between the surface and inside of the casting and is closely related to the temperature difference during solidification of the casting.
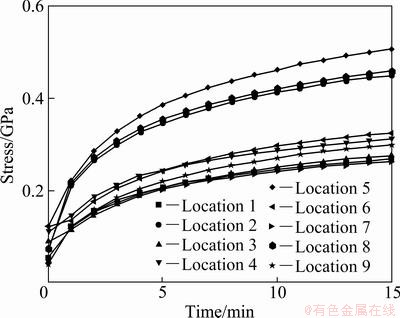
Fig. 10 Stress distribution inside casting by numerical analysis (AC7A casting material)
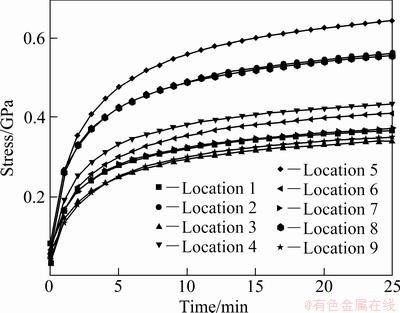
Fig. 11 Stress distribution inside casting by numerical analysis (AC4C casting material)
4 Conclusions
1) The numerical results of temperature distribution predicted the rapid heat transfer from initial state to 3 min. More than all, the temperature of middle part inside the casting is higher than that at contact parts of the casting and the metal casting device.
2) The temperature distributions of two casting materials are almost uniformly maintained about 5 and 12 min due to the phase change process, respectively. The solidification patterns except for phase change process have almost similar results when the temperature distribution of experimental result is compared with that of numerical result.
3) According to thermal deformation results of two casting materials, displacement and stress of AC7A casting material are approximately 0.6 mm and 0.17 GPa lowers than those of AC4C casting material, respectively.
4) Thermal deformation is generated by the temperature difference between the surface and inside of the casting and is closely related to the temperature difference during solidification process.
References
[1] KIM G W, JUNG H S, CHO J R, YANG Y S. Finite element analysis in residual aligning torque and frictional energy of a tire with detailed tread blocks [J]. Transactions of KSAE,2004, 12(4): 173-180.
[2] OH Y K, YOON H S, YANG H D. A study on thermal deformation of AC4C aluminum alloy casting material for tire mold in metal casting method [J]. International Journal of Modern Physics B,2010, 24(15-16): 2243-2248.
[3] RAFIQUE M M A, LQBAL J. Modeling and simulation of heat transfer phenomena during investment casting [J]. International Journal of Heat and Mass Transfer, 2009, 52(7-8): 2132-2139.
[4] THOMAS B G, NAJJAR F M. Finite element modelling of turbulent fluid flow and heat transfer in continuous casting [J]. Applied Mathematical Modeling, 1991, 15(5): 226-243.
[5] MIRBAGHERI S M H, DADASHZADEH M, SERAJZADEH S, TAHERI A K, DAVAMI P. Simulation of melt flow in coated mould cavity in the casting process [J]. Journal of Materials Processing Technology, 2003, 142(2): 493-507.
[6] MIRBAGHERI S M H, DADASHZADEH M, SERAJZADEH S, TAHERI A K, DAVAMI P. Modeling the effect of mould wall roughness on the melt flow simulation in casting process [J]. Applied Mathematical Modelling, 2004, 28(11): 933-956.
[7] LIU X J, BHAVNANI S H, OVERFELT R A. Simulation of EPS foam decomposition in the lost foam casting process [J]. Journal of Materials Processing Technology, 2007, 182(1-3): 333-342.
[8] SHEPEL S V, PAOLUCCI M. Numerical simulation of filling and solidification of permanent mold castings [J]. Applied Thermal Engineering,2002, 22: 229-248.
[9] VIJAYARAM T R, SULAIMAN S, HAMOUDA A M S, AHMAD M H M. Numerical simulation of casting solidification in permanent metallic molds [J]. Journal of Materials Processing Technology, 2006, 178: 29-33.
[10] HONG C P, UMEDA T, KIMURA Y. Boundary elements [M]. Berlin: Spring-Verlag, 1983: 153.
[11] KANG S, ZABARAS N. Control of the freezing interface motion in two-dimensional solidification processes using the adjoint method [J]. International Journal for Numerical Methods in Engineering, 1995, 38(1): 63-80.
[12] RICHMOND O, TIEN R H. Thermal stress and air-gap formation during the early stages of solidification in a rectangular mold [J]. Journal of Mechanics, 1971, 49: 481-486.
[13] ASM International Handbook Committee. Metals handbook, Vol. 1: Properties and selection: Irons, steels, and high-performance alloys [M]. Ohio: ASM International, 1990.
[14] PECKNER D, BERNSTEIN I M. Handbook of stainless steels [M]. New York: McGraw-Hill Book Company, 1977.
(Edited by ZHAO Jun)
Foundation item: Project supported by Research Funds from Chosun University (2009), Korea
Corresponding author: Yool-Kwon OH; Tel: +82-62-2307010; E-mail: ygoh@chosun.ac.kr
DOI: 10.1016/S1003-6326(12)61816-0
