
J. Cent. South Univ. (2020) 27: 2754-2762
DOI: https://doi.org/10.1007/s11771-020-4496-6
Thermodynamic optimization for a quantum thermoacoustic refrigeration micro-cycle
E Qing(鄂青)1, 2, WU Feng(吴锋)1, 2, CHEN Lin-gen(陈林根)2, QIU Yi-nan(邱一男)3
1. School of Optical Information and Energy Engineering, Wuhan Institute of Technology,Wuhan 430205, China;
2. Institute of Thermal Science and Power Engineering, Wuhan Institute of Technology,Wuhan 430205, China;
3. State Key Laboratory of Technologies in Space Cryogenic Propellants, Beijing 100028, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: A model of quantum thermoacoustic refrigeration micro-cycle (QTARMC) is established in which heat leakage is considered. A single particle contained in a one-dimensional harmonic potential well is studied, and the system consists of countless replicas. Each particle is confined in its own potential well, whose occupation probabilities can be expressed by the thermal equilibrium Gibbs distributions. Based on the Schrodinger equation, the expressions of coefficient of performance (COP) and cooling rate for the refrigerator are obtained. Effects of heat leakage on the optimal performance are discussed. The optimal performance region of the refrigeration cycle is obtained by the using of Ω objective function. The results obtained can enrich the thermoacoustic theory and expand the application of quantum thermodynamics.
Key words: thermoacoustic refrigeration; quantum mechanics; thermal phonon; performance optimization; finite time thermodynamics
Cite this article as: E Qing, WU Feng, CHEN Lin-gen, QIU Yi-nan. Thermodynamic optimization for a quantum thermoacoustic refrigeration micro-cycle [J]. Journal of Central South University, 2020, 27(9): 2754-2762. DOI: https://doi.org/10.1007/s11771-020-4496-6.
1 Introduction
The so-called thermoacoustic effect is a conversion phenomenon between heat energy and sound energy. It is a time averaged energy effect resulting from the heat interaction between the first medium (compressible fluid) and the second medium (solid wall). Broadly speaking, it is the interaction and coupling between the oscillation process and diffusion process. In a narrow sense, it is the direct conversion of heat energy and ordered sound energy [1]. Thermoacoustic engine (including heat engine and refrigerator) is a type of machine in which the energy conversion is realized by thermoacoustic effect [1-4]. In recent years, because of its unique advantages, without the moving parts, the thermoacoustic engine has attracted attentions of many scholars in many fields in the world. Great progress has been made in both theory [5] and application researches [6-9].
The study of finite time thermodynamics is extended from classical to the quantum thermodynamic system [10], and the quantum mechanics method is applied to the performance analyses and optimization of thermodynamic cycles. In 1992, GEVA et al [11, 12] firstly studied the performance of quantum Carnot heat engine. Since then, a large number of studies have been carried out to study the performance of quantum engines [13-19] with ideal quantum gas as working medium. In the accurate analysis of the quantum thermodynamic cycle, the heat transfer loss, the internal loss of the working fluid system [20] and the irreversible loss of the bypass heat leakage [21] were considered. Many meaningful concepts and conclusions were obtained.
In the study of thermoacoustic heat engine miniaturization [22-25], it was found that classical thermodynamic theory has some disadvantages. For example, the classical thermodynamics is difficult to analyze and calculate the interaction between heat and sound. Therefore, some authors attempted to use quantum theory to study the thermoacoustic cycle. WU et al [19] studied the influence of quantum degeneracy on the performance of a thermoacoustic micro-cycle. In this paper, based on the above researches, a model of irreversible quantum thermoacoustic refrigeration micro-cycle (QTARMC) working in a 1D harmonic trap will be established. Considering the heat leakage between two ends, the performance parameters and the Ω objective function for coordinating these parameters of the cycle will be obtained. The results of this paper have certain universality and tolerance, and have some theoretical significance to study the quantum thermoacoustic refrigerator.
2 Thermoacoustic refrigeration micro- cycle
SWIFT [1] put forward the concept of thermoacoustic refrigeration micro-cycle (TARMC) as early as 1988. The schematic diagram of TARMC is shown in Figure 1.
As shown in Figure 1, a small gas parcel inside the regenerator is used as a sample to investigate the four processes of a TARMC. Each TARMC consists of two isobaric and two adiabatic processes.
The basic unit of thermoacoustic oscillation is the thermoacoustic mesoscale parcel. It is the basis of the classical thermoacoustic micro thermodynamics cycle. These parcels are composed of a large number of molecules or atoms with statistical significance (such as nitrogen molecules, helium molecules, etc. in the working fluid). The basis for the QTARMC, which is studied in this work, is still the thermoacoustic parcel, which is composed of many identical microscopic particles (such as nitrogen molecules, helium molecules, etc.). These microscopic particles have the characteristics of simple harmonic oscillation under the action of sound field. In quantum acoustics, quantized sound waves are called acoustic quanta or phonons. Therefore, one calls these microscopic particles thermal phonons. Thermal phonons belong to the Bose system, so the evolution of each thermal phonon should obey the Schrodinger equation of quantum mechanics.
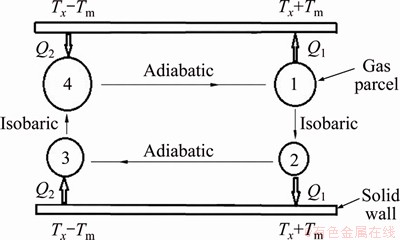
Figure 1 Schematic diagram of TARMC
In the thermoacoustic effect, with the help of harmonic sound wave, thermoacoustic refrigeration is achieved, i.e., heat is pumped from the cold end to the hot end. In quantum mechanics, the action of the microscopic particles is controlled by the potential function. Correspondingly, in the quantum thermoacoustic refrigeration cycle, the effect of sound waves on the thermal phonon can be represented by a harmonic oscillator potential well with a width of L. In the evolution process of thermal phonon, the width of the harmonic trap L changes continuously, the minimum value is L2, and the maximum value is L4. For a single thermal phonon, one can use the parameter force instead of the parameter pressure in the classical cycle. Thus QTARMC is obtained, and the schematic diagram of it is shown in Figure 2.
As shown in Figure 2, the processes 2-3 and 4-1 are quantum adiabatic. Here, the quantum adiabatic process is defined: the trap width L is variable, the energy eigenvalues of each level are changed, but the occupation probability at each energy level is not changed. That is, there is no energy level transition in such a process,but the work exchange between the system and the surroundings results in a change in the thermodynamic energy of the system.
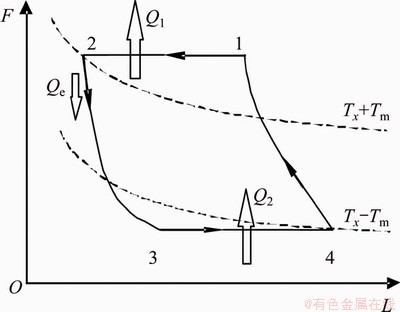
Figure 2 F-L diagram of a QTARMC
The processes 1-2 and 3-4 (see Figure 2) in the QTARMC are two constant force processes. Due to the characteristics of thermoacoustic oscillation, the wall temperatures of thermoacoustic regenerator, in two constant force processes, are Tx+Tm and Tx-Tm, respectively, where Tx is the local mean temperature, subscript x represents the local coordinates of phonon, 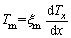 is the temperature amplitude value, ξm is the amplitude of vibration displacement, and
is the temperature amplitude value, ξm is the amplitude of vibration displacement, and  is the longitudinal temperature gradient of the solid wall of the regenerator. According to the second law of thermodynamics, the temperature of the system should be not less than Tx+Tm in the exothermic process 1-2, and the temperature of the system should be not more than Tx-Tm in the endothermic process 3-4. From the point of view of quantum mechanics, constant force process can be defined: the trap width L is variable, the occupation probability at each energy level is changed too, but the force is unchanged. That is, there is energy level transition in such process, and the heat and work exchange between the system and the surroundings results in a change in the thermodynamic energy of the system.
is the longitudinal temperature gradient of the solid wall of the regenerator. According to the second law of thermodynamics, the temperature of the system should be not less than Tx+Tm in the exothermic process 1-2, and the temperature of the system should be not more than Tx-Tm in the endothermic process 3-4. From the point of view of quantum mechanics, constant force process can be defined: the trap width L is variable, the occupation probability at each energy level is changed too, but the force is unchanged. That is, there is energy level transition in such process, and the heat and work exchange between the system and the surroundings results in a change in the thermodynamic energy of the system.
In an actual thermoacoustic regenerator, there is a certain bypass heat leakage in the solid medium which connects the high and low temperature ends, just like Qe in Figure 2. Sometimes, the amount of heat leakage in this part is so large that one can’t ignore it directly during system cycle calculation.
For convenience, one considers only the two- level system, i.e., only two energy levels per phonon. It is assumed that the occupation probability of thermal phonon in the excited state is governed by the Gibbs distribution.
3 Quantum thermodynamics of system
In a thermoacoustic refrigerator, gas parcels move back and forth under acoustic excitation. In the quantum mechanical model, the harmonic potential field of the particle (thermal phonon) system is:
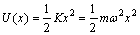 (1)
(1)
where K,x and m are the elasticity, the displacement and the mass of the particle (thermal phonon), respectively; 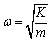 is the natural angular frequency of the harmonic oscillator. Based on quantum mechanics rules, the energy operator of the system is the Hamiltonian, and it can be written as [26]:
is the natural angular frequency of the harmonic oscillator. Based on quantum mechanics rules, the energy operator of the system is the Hamiltonian, and it can be written as [26]:
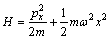 (2)
(2)
where px is momentum operator. The energy eigenvalues En of the system can be obtained by solving the Schrodinger equation.
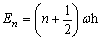 (n= 0, 1, 2, …, ∞) (3)
(n= 0, 1, 2, …, ∞) (3)
where 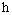 is reduced Planck’s constant and n is oscillation quantum number. The relationship between the characteristic length L and angular frequency ω of a harmonic potential trap is
is reduced Planck’s constant and n is oscillation quantum number. The relationship between the characteristic length L and angular frequency ω of a harmonic potential trap is
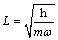 (4)
(4)
Substituting Eq. (4) into Eq. (3) yields:
 (n= 0, 1, 2, …, ∞) (5)
(n= 0, 1, 2, …, ∞) (5)
Obviously, the system is in each energy eigenstate at a certain probability. So, the energy of the system can be written as:
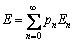 (6)
(6)
where pn (n=0, 1, 2, …, ∞) is the occupation probability in the n-th eigenstate, and they should satisfy the normalized condition:
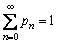 (7)
(7)
For a two-level system (n=0, 1), the energy of the system in the thermodynamic stage i can be obtained from Eqs. (5)-(7):
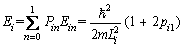 (i= 1, 2, 3, 4) (8)
(i= 1, 2, 3, 4) (8)
where i corresponds to the 4 stages in Figure 2; pi1 is the occupation probability in the excited state (n=1) when the thermal phonon is at stage of i. For quantum adiabatic processes 2-3 and 4-1, the energy eigenvalue of each level is changed but the occupation probability under each energy level is not changed [27]. Therefore,
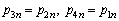 (n=0, 1) (9)
(n=0, 1) (9)
The energy of thermal phonon in stages of 1, 2, 3 and 4 can be obtained from Eqs. (8) and (9):
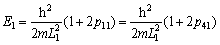 (10)
(10)
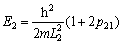 (11)
(11)
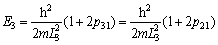 (12)
(12)
 (13)
(13)
Because the work exchange between the system and the surroundings results in a change in the energy of the system in quantum adiabatic processes, the generalized force is:
 (14)
(14)
where W is the work. So, for a two-level system (n=0, 1), the forces on thermal phonon at stages of 1, 2, 3 and 4 are:
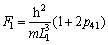 (15)
(15)
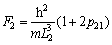 (16)
(16)
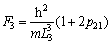 (17)
(17)
 (18)
(18)
For the constant force processes 1-2 and 3-4, F1=F2 and F3=F4. So,
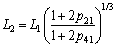 (19)
(19)
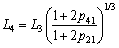 (20)
(20)
The working fluid of QTARMC is composed of many identical particles (thermal phonons) which satisfy all the above evolution laws. Suppose that the occupation probability of the thermal phonons in the excited state satisfies the Gibbs distribution, then [28]:
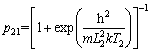 (21)
(21)
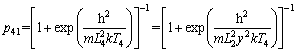 (22)
(22)
where k is the Boltzmann constant and width ratio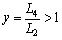 .
.
For the convenience of calculation, the temperatures of stage 2 and stage 4 (see Figure 2) are selected as the following:
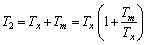 (23a)
(23a)
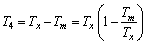 (23b)
(23b)
According to the First Law of thermodynamics, the heat exchanges between the system and the solid wall in constant force processes 1-2 and 3-4 are:
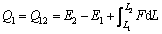 (24a)
(24a)
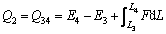 (24b)
(24b)
So,
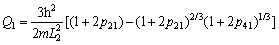 (25)
(25)
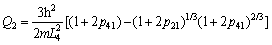 (26)
(26)
Along the solid wall of the regenerator, there exists a longitudinal heat leakage. The thermal leakage rate is selected as following [29]:
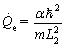 (27)
(27)
where constant α is thermal leakage coefficient. Then, the heat leakage per cycle is:
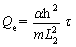 (28)
(28)
where τ is the cycle time. Assuming that the width of the trap L changes at the mean speed of 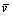 [30-32], the cycle period of 1-2-3-4-1 is:
[30-32], the cycle period of 1-2-3-4-1 is:
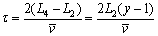 (29)
(29)
Thus, the effective heat transfer at the hot end and the cold end can be expressed respectively as:
 (30a)
(30a)
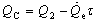 (30b)
(30b)
That is,

 (31)
(31)
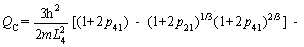
 (32)
(32)
4 Performance parameters and Ω objective function
The coefficient of performance (COP) of refrigerating cycle is
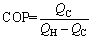 (33)
(33)
Substituting Eqs.(31) and (32) into Eq. (33) yields:
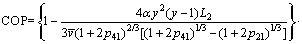
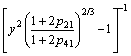 (34)
(34)
Let 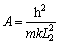 and
and 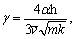 Eq. (34) can be rewritten as:
Eq. (34) can be rewritten as:
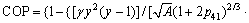
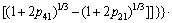
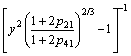 (35)
(35)
The cooling rate of the cycle is:
 (36)
(36)
Dimensionless processing of R can be defined as the dimensionless cooling rate:
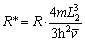 (37)
(37)
Substituting Eqs. (26), (27), (29) and (36) into Eq. (37) yields:
 (38)
(38)
Generally speaking, when the cooling rate is the largest, COP is not the largest, and vice versa. In the optimization of heat engines, CALVO- HERNANDEZ et al [33] provided a function Ω to consider the comprehensive effect of power output and thermal efficiency. In the same idea, to study the coordination optimization performance of QTARMC, a function Ω is chosen as the objective function of optimization. It is defined as:
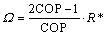 (39)
(39)
The cooperation optimization between cooling rate and COP is taken into account by the Ω function. It avoids the calculation of entropy included in the expression of conventional ecological optimization function.
It is known from Eqs. (35), (38) and (39) that if the Gibbs distribution is taken into account for a given temperature range, R*, COP and the Ω function are all the functions of the potential trap width L2 (i.e., A), the width ratio y, and the thermal leakage coefficient α (i.e., γ).
5 Numerical examples and discussions
5.1 Influences of A and width ratio y on dimensionless cooling rate R* and COP
As shown in Eqs. (21), (22), (38) and (35), R* and COP of the cycle are both functions of A and y for given Tx, γ and Tm/Tx. Once the temperatures of two ends and the working mediums are known, the values of Tx, γ and Tm/Tx can be determined. Then, the maximizations of R* and COP can be carried out numerically. A three-dimensional diagram (A, y, R*) with Tx=280 K, γ=0.2 and Tm/Tx=0.1 is shown in Figure 3. A three-dimensional diagram (A, y, COP) with Tx=280 K, γ=0.2 and Tm/Tx=0.1 is shown in Figure 4. As shown in these two figures, there exist the maximum values for R* and COP though these two maximum values appear in different coordinates.
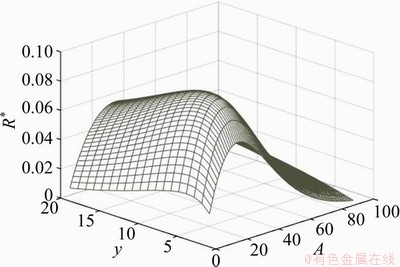
Figure 3 Dimensionless cooling rate R* as a function of A and y (Tx=280 K, γ=0.2 and Tm/Tx=0.1)
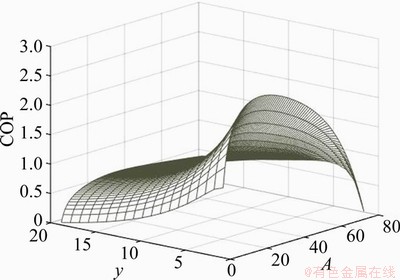
Figure 4 Coefficient of performance COP as a function of A and y (Tx=280 K, γ=0.2 and Tm/Tx=0.1)
5.2 Influences of A and width ratio y on Ω objective function
It can be seen from Eqs. (35), (38) and (39) that the Ω objective function is also a function of A and y for given Tx, γ and Tm/Tx. A three-dimensional diagram (A, y, Ω) with Tx=280 K, γ=0.2 and Tm/Tx=0.1 is shown in Figure 5. The figure shows that there is only one best combination of A and y which leads to the maximum Ω objective function for given parameters. For each given A (i.e. L2), a maximum Ω objective function and a corresponding y are always there.
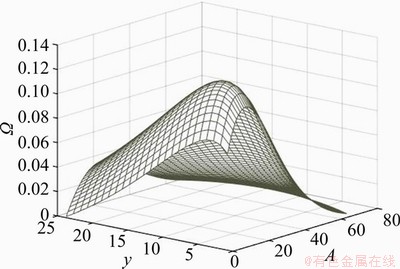
Figure 5 Ω objective function as a function of A and y (Tx=280 K, γ=0.2 and Tm/Tx=0.1)
5.3 Influences of A on Ω versus COP and R* versus COP
According to the previous analyses, the characteristics of Ω objective function versus COP are investigated. Equations (35), (38) and (39) give a fundamental relation between Ω(A, y) and COP(A, y) for discussing the optimal performance of the QTARMC. The Ω versus COP characteristic is dependent on y for given A and other parameters as the same as those used in Figure 3. The optimal characteristic curves of Ω objective function versus COP(Ω-COP) are shown in Figure 6. By the same method, the optimal characteristic curves of R*-COP are shown in Figure 6 too.
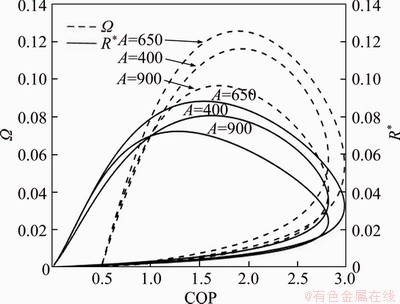
Figure 6 Effects of A on Ω versus COP and effects of A on R* versus COP (Tx=280 K, γ=0.2 and Tm/Tx=0.1)
Obviously, there are a maximum R*max and a corresponding COPR, and a maximum COPmax and a corresponding R*0. According to R*-COP curves, the optimization region of QTARMC should be:
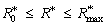 and
and 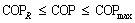 (40)
(40)
In the same way, there are a maximum Ωmax and a corresponding COPΩ, and a maximum COPmax and a corresponding Ω0. According to Ω-COP curves, the optimization region of QTARMC is as follows:
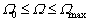 and
and 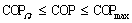 (41)
(41)
From Figure 6, one can see clearly that the region defined by Eq. (41) is inside of the region defined by Eq. (40). And COPΩ is larger than COPR. So, the region defined by Eq. (41) is the real optimization region of QTARMC, and the function Ω is suitable for being used as the objective function of optimization for QTARMC.
5.4 Influences of thermal leakage γ on Ω, COP and R*
Considering the heat leakage between the hot end and the cold end, the cycle performance parameters and the Ω objective function representing the coordination optimization performance of the cycle are obtained. The effects of thermal leakage γ on Ω, COP and R* are shown in Figure 7. Obviously, the less the thermal leakage is, the faster the R* is, the higher the COP is. That is, the decrease of the thermal leakage can improve the performance of QTARMC.
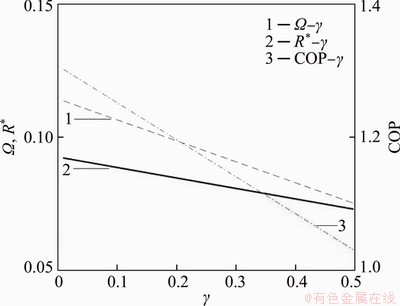
Figure 7 Effects of thermal leakage γ on Ω, COP and R* (Tx=280 K, y=1.4, A=650 and Tm/Tx=0.1)
6 Conclusions
In this paper, an irreversible quantum thermoacoustic refrigerator with heat leakage is investigated. The model of QTARMC consists of two constant force branches and two quantum adiabatic branches. Considering heat leakage, the expressions of some performance parameters are derived. The effects of heat leakage on the COP and R* are analyzed. The optimal performance region is obtained through optimization analyses. The results provide a new method for studying the thermoacoustics and broaden the applied range of the quantum thermodynamics.
The findings show that the reduction of heat leakage is beneficial to the improvement of cycling performance. The analyses of this paper provide a theoretical basis for the performance evaluation and improvement of quantum thermoacoustic refrigerators.
One extension of this paper would be to study the optimal performance of a reverse thermoacoustic engine with the similar method discussed herein. Another meaningful ideal which may be taken into account is to analyze a multilevel system, and investigate the optimal criteria of the system. Both the ideals mentioned above deserve continuing research in the optimization analyses of irreversible quantum thermoacoustic engines.
Contributors
The overarching research goals were developed by E Qing, WU Feng, CHEN Lin-gen. WU Feng provided the idea of the research. E Qing completed the analysis, validation, and wrote the draft of manuscript. CHEN Lin-gen and Qiu Yi-nan reviewed and edited the draft of manuscript.
Conflict of interest
E Qing, WU Feng, CHEN Lin-gen, QIU Yi-nan declare that they have no conflict of interest.
References
[1] SWIFT G W. Thermoacoustic engine [J]. J Acoust Soc Am, 1988, 84(4): 1145-1180. DOI: 10.1121/1.396617.
[2] WU F, LI Q, GUO F Z, SHU A Q. Advance in thermoacoustic theory [J]. J Wuhan Inst Tech, 2012, 34(1): 1-6. DOI: 10.3969/j.issn.1674. (in Chinese)
[3] HARIHARAN N M, SIVASHANMUGAM P, KASTHURIRENGAN S. Studies on performance of thermoacoustic prime mover [J]. Experimental Heat Transfer, 2015, 28: 267-281. DOI: 0.1080/08916152.2013.871605.
[4] WU F, SHU A Q, GUO F Z, WAN T. Thermoacoustic oscillation basing on parameter exciting [J]. Energy, 2014, 68: 370-376. DOI: 10.1016/j.energy.2014.02.072.
[5] GUO F Z, LI Q. Heat dynamics [M]. Wuhan: Huazhong University of Science & Technology Press, 2007. (in Chinese)
[6] TIJANI M E H, ZEEGERS J C H, de WAELE A T A M. Design of thermoacoustic refrigerators [J]. Cryogenics, 2002, 42(1): 49-57. DOI: 10.1016/s0011-2275(01)00179-5.
[7] SWIFT G W. Thermoacoustics: A unifying perspective for some engines and refrigerators [J]. J Acoust Soc Am, 2003, 113(5): 2379-2381.
[8] GARRETT S L, ADEFF J A, HOFLER T J. A thermoacoustic refrigerator for space applications [J]. Trans AIAA J Thermophys & Heat Transfer, 2012, 85(7): 595-599. DOI: 10.1121/1.401096.
[9] DAI W, LUO E C, HU J Y, LING H. A heat-driven thermoacoustic cooler capable of reaching liquid nitrogen temperature [J]. Appl Phys Lett, 2005, 86(22): 779-785. DOI: 10.1063/1.1941472.
[10] KOSLOFF R. Quantum thermodynamics: A dynamical viewpoit [J]. Entropy, 2013, 15(6): 2100-2128. DOI: 10.3390/e15062100.
[11] GEVA E, KOSLOFF R. A quantum-mechanical heat engine operating in finite time: A model consisting of spin-1/2 systems as working fluid [J]. J Chem Phys, 1992, 96(4): 3054-3067. DOI: 10.1063/1.461951.
[12] GEVA E, KOSLOFF R. On the classical limit of quantum thermodynamics in finite time [J]. J Chem Phys, 1992, 97(6): 4398-4412. DOI: 10.1063/1.463909.
[13] WU F, CHEN L G, SUN F R, WU C. Finite-time exergoeconomic performance bound for a quantum Stirling engine [J]. Int J Eng Sci, 2000, 38(2): 239-247. DOI: 10.1016/s0020-7225(99)00025-7.
[14] WU F, CHEN L G, SUN F R, ZHU Y H. Performance and optimization criteria for forward and reverse quantum Stirling cycles [J]. Energy Convers Mgmt, 1998, 39(8): 733-739. DOI:10.1016/s0140-6701(98)96841-2.
[15] WANG J H, HE J Z, MAO Z Y. Performance of a quantum heat engine cycle working with harmonic oscillator systems [J]. Sci in China, Series G, Phys, Mech & Astron, 2007, 50(2): 163-176. DOI:10.1007/s11433-007-0006-1.
[16] WU F, YANG Z Z, CHEN L G, LIU X W. Work output and efficiency of a reversible quantum Otto cycle [J]. Thermal Sci,2010,14(4): 879-886. DOI: 10.2298/tsci1004879w.
[17] CHEN L G, LIU X W, GE Y L, WU F, SUN F R. Ecological optimization of irreversible harmonic oscillator Carnot refrigerator [J]. J Energy Instit,2016,86(2): 85-96. DOI: 10.1179/1743967112z.00000000049.
[18] LIU S N, OU C J. Maximum power output of quantum heat engine with energy bath [J]. Entropy, 2016, 18(6): 205. DOI: 10.3390/e18060205.
[19] WU F, CHEN L G, LI Q, WU C. Thermodynamic performance on a thermoacoustic micro-cycle under the condition of weak gas degeneracy [J]. Appl Energy, 2009, 86(7, 8): 1119-1123. DOI: 10.1016/j.apenergy.2008.07.001.
[20] FELDMANN T, KOSLOFF R. Performance of discrete heat engines and heat pumps in finite time [J]. Phys Rev E, 2000, 61(5): 4774-4790. DOI: 10.1103/physreve.61.4774.
[21] LIU X W, CHEN L G, WU F, SUN F R. Ecological optimization of an irreversible quantum Carnot heat engine with spin-1/2 systems [J]. Phys Scr, 2010, 81(2): 025003. DOI: 10.1088/0031-8949/81/02/025003.
[22] HOFLER T J. Development of a miniature thermoacoustic refrigerator [J]. J Acous Soc Am, 2000, 108(5): 2554-2560. DOI: 10.1121/1.4743480.
[23] SYMKO O G, ABDEL-RAHMAN E, KWON Y S, EMMI M, BEHUNIN R. Design and development of high-frequency thermoacoustic engines for thermal management in microelectronics [J]. Microelectron J, 2004, 35(2): 185-191. DOI: 10.1016/j.mejo.2003.09.017.
[24] LUO D L, WU F, GUO F Z, ZHANG C P. Optimization design of the hot end heat exchanger in subminiature heat-driven thermoacoustic acoustic engine [J]. Cryo & Supercon, 2006, 34(4): 258-262. DOI: CNKI:SUN:DWYC. 0.2006-04-006. (in Chinese)
[25] DENYS P. Performance measurement of a mini thermoacoustic refrigerator and associated drivers [D]. Naval Postgraduate School, 2002.
[26] MESSIAH A. Quantum mechanics [M]. New York: Dover Publications, 1999.
[27] KIEU T D. The second law, Maxwell’s demon, and work derivable from quantum heat engines [J]. Phys Rev Lett, 2004, 93(14): 140403. DOI: 10.1103/physrevlett.93.140403.
[28] HE X, HE J Z. Thermal entangled four-level quantum Otto heat engine [J]. Sci in China, Series G: Phy, Mech & Astron, 2012, 55(10): 1751-1756. DOI: 10.1007/s11433- 012-4835-1.
[29] YIN Y, CHEN L G, WU F. Optimal power and efficiency of quantum Stirling heat engines [J]. Eur Phys J Plus, 2017, 132(1): 45. DOI: 10.1140/epjp/i2017-11325-0.
[30] von SPAKOVSKY M R, GEMMER J. Some trends in quantum thermodynamics [J]. Entropy, 2014, 16(6): 3434-3470. DOI: 10.3390/e16063434.
[31] E Qing, WU Feng, YIN Yong, LIU Xiao-wei. Optimal power and efficiency of quantum thermoacoustic micro-cycle working in 1D harmonic trap [J]. Journal of Low Temperature Physics, 2017, 189(1, 2): 84-97. DOI: 10.1007/s10909-017-1791-1.
[32] E Qing, WU Feng. Performance analysis for quantum thermoacoustic refrigeration micro-cycle working in generalized 1D potential [J]. Journal of Central South University (Science and Technology), 2019, 50(3): 726-733. DOI: 10.11817/j.issn.1672-7207.2019.03.028. (in Chinese)
[33] CALVO-HERNANDEZ A, MEDINA A, ROCO J M M. Time, entropy generation, and optimization in low- dissipation heat devices [J]. New Journal of Physics, 2015, 17: 075011. DOI: 10.1088/1367-2630/18/1/019501.
(Edited by YANG Hua)
中文导读
量子热声制冷微循环的热力学优化
摘要:本文建立了一个考虑热漏影响的量子热声制冷微循环模型。研究主要围绕一维谐振势阱中的单个粒子展开,而系统是由无数个这样的粒子组成的。每个粒子都被限制在一定的势阱中,其出现几率可用热平衡吉布斯分布来描述。本文基于薛定谔方程推出了制冷机性能系数和制冷速率的表达式;讨论了热泄漏对循环优化性能的影响;利用Ω目标函数得出了制冷循环的最优性能区域。所得结果不仅丰富了热声理论,而且拓展了量子热力学的应用。
关键词:热声制冷;量子力学;热声子;性能优化;有限时间热力学
Foundation item: Project(51176143) supported by the National Natural Science Foundation of China; Project(K201919) supported by the Scientific Research Foundation of Wuhan Institute of Technology, China
Received date: 2020-01-14; Accepted date: 2020-06-22
Corresponding author: WU Feng, PhD, Professor; Tel: +86-27-87194673; E-mail: wufeng@wit.edu.cn; ORCID: https://orcid.org/ 0000-0001-6697-4287; E Qing, PhD, Associate Professor; E-mail: eqinghust@163.com; ORCID: https://orcid. org/0000-0002-4195-3524