


Trans. Nonferrous Met. Soc. China 22(2012) 2444-2450
Scale effect mechanism on micro rod upsetting deformation analyzed by crystal plasticity model
CHENG Li-dong1, WANG Zhen-long1, 2
1. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China;
2. Key Laboratory of Micro-systems and Micro-structures Manufacturing of Ministry of Education,
Harbin Institute of Technology, Harbin 150001, China
Received 9 July 2012; accepted 10 August 2012
Abstract: To analyze the effect of single grain deformation behaviors on microforming process, a crystal plasticity model was developed considering grains at free surface layer as single grains. Based on the rate-dependent crystal plasticity theory, the analysis of the scale effect mechanism on upsetting deformation of micro rods was performed with respect to specimen dimension, original grain orientation and its distribution. The results show that flow stress decreases significantly with the scaling down of the specimen. The distribution of the grain orientation has an evident effect on flow stress of the micro specimen, and the effect becomes smaller with the progress of plastic deformation. For the anisotropy of single grains, inhomogeneous deformation occurs at the surface layer, which leads to the increase of surface roughness, especially for small specimens. The effect of grain anisotropy on the surface topography can be decreased by the transition grains. The simulation results are validated by upsetting deformation experiments. This indicates that the developed model is suitable for the analysis of microforming processes with characteristics, such as scale dependency, scatter of flow stress and inhomogeneous deformation.
Key words: microforming; scale effect; crystal plasticity; crystal orientation
1 Introduction
With the rapid development of micro- electro-mechanical systems (MEMS) and micro-system technologies (MST), more and more microparts used in these systems are required in greater quantities [1]. Forming technology seems to be more suitable for meeting the demands of serial production due to its high production output [2]. Microforming is a metal forming process, which is understood to be the production of parts or structures with at least two dimensions in the submillimeter range. For the existence of the size-scale effect, the knowledge of microforming processes is mainly based on in-house experience and trial and error procedures, which prevents the transfer of existing know-how of standard forming processing with conventional dimensions. With geometrically similar tensile and hydraulic bulging tests, the flow stress of thin sheet was found to decrease with the decrease of specimen dimensions [3]. The influence of the material microstructure on the mechanical properties of metal foils was discussed with thicknesses ranging from 25 to 500 μm [4]. In bulk metal forming, the scale effect on the micro-scale plastic deformation was investigated via micro-cylindrical compression test [5,6]. Based on the theory of metal physics, a mesoscopic model was developed considering different grain structures to analyze the scatter of the process factors [7]. By generating grain structure, the influence of grain size and its position was taken into account in the mesoscopic model [8]. It was found that the ratio of grain size to feature dimension had an obvious effect on the size-scale effect. The experiments showed a decrease of the yield strength with a decreasing number of grains over the thickness up to one grain over the thickness. For the grain with size larger than the thickness of specimen, the yield strength tends to increase with increasing the grain size [9]. A new constitutive model considering parameter T/D (thickness/average grain size) was proposed, and the size effect of the flow stress was analyzed in details [10].
In this work, the scale dependent characteristics of micro metal polycrystalline rod deformation were studied by developing an analysis model based on the crystal plasticity theory. For lower constriction, the grains at the free surface layer of a micro rod were treated as single grains, and their deformation behavior was analyzed by using a crystal constitutive model based on the rate-dependent crystal plasticity theory. With the same grain size, the scale effect of micro rod dimension on flow stress was investigated, and the scatter of flow stress was analyzed by changing the distribution of original grain orientation. The effects of the original grain orientation and its distribution on the inhomogeneous deformation were studied systemically. The simulation results were proved by the upsetting deformation experiments with micro copper rods.
2 Procedure of FE simulation applying crystal plasticity theory
2.1 Analysis model for micro rod upsetting deformation
When the dimensions of a specimen are scaled down to the submillimeter range, there are only several grains in the radial direction as shown in Fig. 1. Every single grain in the micro specimen plays an important role during the plastic deformation. From the physical mechanism of the metal plastic deformation, the grain boundaries are work-hardened for the increase of dislocation density which is resulted from the accumulation of dislocations. With the miniaturization of the specimen, the situation is changed for the free surface effect. The dislocation segments near the free boundaries tend to move towards the free boundary and annihilate [11]. It is found that hardening zones originate not from the grain boundary regions but rather concentrate at grain boundary triple junctions [12]. Therefore, the grain boundary strengthening effect dwindles at the free surface layer and further leads to the flow stress decrease of the whole specimen. The deformation behavior of grains at the free surface layer is near to that of single grains, and the characteristics of a single grain, such as elastic anisotropy, grain orientation and its distribution, should be considered in microforming. To analyze the mechanism of the scale effect during the miniaturization, the grains at free surface layer are treated as single grains and analyzed with crystal plasticity theory. The grain boundary sliding and hardening are precluded, and the grain boundaries are modeled as being perfectly bonded. Considering that the internal grains are restricted by neighboring grains, the plastic deformation tends to be uniform like that in traditional macroforming which can be analyzed with continuum mechanics. A classical FE method is chosen to analyze the deformation of internal grains of micro rod specimen, as shown in Fig. 2.
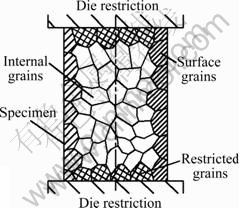
Fig. 1 Microstructure of polycrystalline micro rod
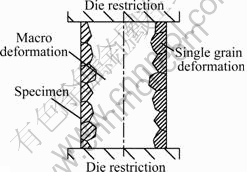
Fig. 2 Analysis model of micro rod
2.2 Crystal constitutive formulation
To analyze the deformation behavior of single grains at the surface layer, a crystal plasticity model is developed based on the rate-dependent single crystal plasticity theory by considering the crystallographic slip and rotation of the crystal lattice during the deformation. The crystal kinematics follows those described by ASARO [13], and the rate-dependent formulation follows that developed by PEIRCE et al [14] and BECHER [15]. The model is implemented as the user subroutine in the commercial finite element code Abaqus used in studies to simulate the deformation of grains.
The rate of Kirchhoff stress is given by
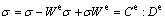 (1)
(1)
where C e is a fourth order tensor of the elastic moduli and σ is the Kirchhoff stress.
Considering the crystal plasticity, Eq. (1) can be rewritten as
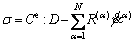 (2)
(2)
 (3)
(3)
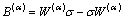 (4)
(4)
Based on the Schmid law, slipping rate 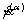 of the αth slip system in a rate-dependent crystalline solid is determined by the corresponding resolved shear stress
of the αth slip system in a rate-dependent crystalline solid is determined by the corresponding resolved shear stress 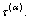
2.3 Foundation of finite element analysis
Based on the analysis above, the partition of micro rod specimen is shown in Fig. 3. Since the grain size is very large compared with the specimen dimension and the amount of grains in micro specimen is very small, it is difficult to obtain a synthetic material microstructure and grain the orientation distribution near a real specimen for the stochastic distribution of grain shape, grain location and grain orientation. In this work, the aim of the investigation is to study the effect of specimen size, grain orientation and its distribution on the plastic deformation behavior of micro rods. So, the grain shape is simplified to a quadrangle, as shown in Fig. 3. Three kinds of typical grain orientations and several kinds of distributions are considered in the analysis. Pure copper is selected as the material, and the parameters of single grain used in crystal constitutive model are listed in Table 1 [14]. The deformation behavior of the polycrystalline part shown in Fig. 4 is obtained with macro rod upsetting deformation at room temperature using Instron 5569 test machine. The dimension of specimen used in upsetting is d 2.8 mm × 4.2 mm, and the grain size is 0.065 mm.
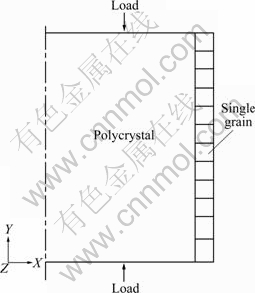
Fig. 3 Partition of micro rod specimen
3 Results and discussion
3.1 Scale dependency of flow stress
The simulation material is selected as FCC pure copper. To compare with the experiment results, the dimensions of micro rod specimens are d 0.81 mm ×1.62 mm and d 1.16 mm × 1.62 mm, respectively. The grain size L of 0.065 mm is assumed, which is the same as that of the micro rod specimen obtained by a heat treatment process. In the simulation, three kinds of original grain orientations (DGO) are assumed. The first kind of original grain orientation (DGO I) is defined as follows: the surface layer grains are assumed to orientate alternatively along two “extremal” orientations, i.e. [001] and [011]. The curves of flow stress vs logarithm strain obtained by simulation and experiment in upsetting deformation are shown in Fig. 5. The comparison of results shows that the simulation results are in good agreement with the experiment data, which indicates that the developed model based on crystal plasticity theory is effective in the analysis of the microforming process.
Table 1 Parameters of Peirce hardening model [14]

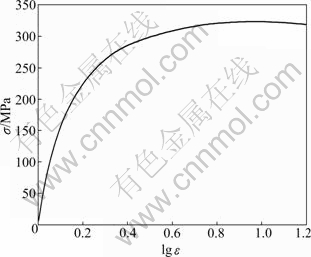
Fig. 4 Stress—logarithm strain (σ—lg ε) curve of pure polycrystalline copper
With the same grain size, the scale effect of the specimen dimension on the flow stress is shown in Fig. 6. An obvious decrease of flow stress is observed when the dimension of specimen is scaled down. This phenomenon indicates that the scale effect of flow stress occurs obviously. It can be analyzed with Eq. (5) from the viewpoint of the metal polycrystalline deformation. The flow stress of the micro specimen is a collective response of single grains. For the lower restriction of grain boundaries, the grains at the free surface layer can be plastically deformed more easily than those in the bulk specimen, which can be proved by the distribution of Mises stress under the reduction in specimen height (RH) of 0.2 mm as shown in Fig. 7. When the grain size is kept constant, the fraction of grains at the free surface layer becomes larger during the scaling down of the specimen, which leads to the decrease of flow stress.
 (5)
(5)
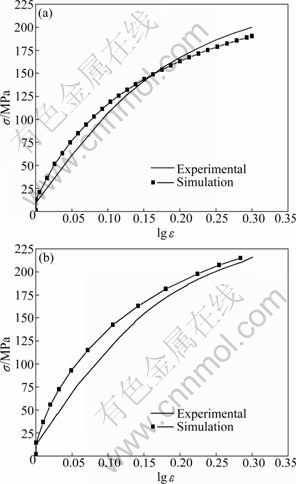
Fig. 5 Flow stress—logarithm strain (σ—lg ε) curves of simulation and test with pure copper: (a) d0.81 mm × 1.62 mm, L=65 μm; (b) d1.16 mm × 1.62 mm, L=65 μm
When the distribution of original grain orientation is changed, the situation is not the same. The second original orientation (DGO II) is assumed as follows: two neighboring grains are regarded as a group with the same grain orientation, and the groups originally orientate along [001] or [011] alternately. The ratio of two grain orientations is also kept at 1.0 (DGO II). The difference of flow stress obtained by DGO I and DGO II is calculated at every logarithm strain, as shown in Fig. 8. The results show that the flow stress of the specimen is changed by the distribution of original grain orientation, which leads to the scatter of the specimen flow stress. The difference of flow stress is 5.3 MPa between distribution I and distribution II at the yield point, which is about 40% of the yield stress. The flow stress of distribution I is larger than that of distribution II. The reason is that two neighboring grains have the same grain orientation in distribution II, which can be considered that the grain size becomes larger, and the flow stress is smaller according to the Hall-Petch relationship. With the progress of the plastic deformation, the grain orientation turns and becomes easier to deform. As a result, the difference of flow stress obtained from two distributions becomes smaller.
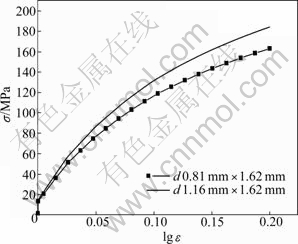
Fig. 6 Flow stress—logarithm strain (σ—lg ε) curves of specimen with different dimensions
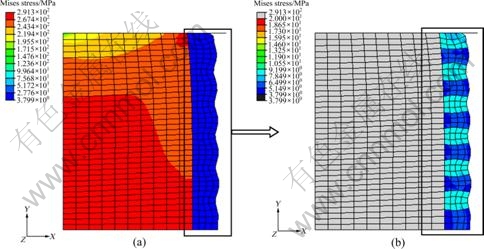
Fig. 7 Distribution of Mises stress in d0.81 mm × 1.62 mm specimen (DGO I, RH 0.2 mm): (a) Throughout specimen; (b) Within surface layer
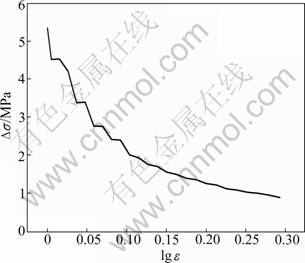
Fig. 8 Curve of stress difference vs logarithm (?σ—lg ε) strain
3.2 Effect of original grain orientation on surface topography
Since the material flows through the crystal lattice via dislocation motion, inhomogeneous deformation occurs in the free surface grains for different grain orientations. The distribution of logarithm strain is shown in Fig. 9 with micro rod specimen of d 0.81 mm × 1.62 mm (DGO I). An inhomogeneous deformation is simulated, and the effect of original grain orientation is so large that it has a clear effect on the surface topography. The free surface of the micro rod specimen presents a wave shape, which may lead to the increase of surface roughness. This phenomenon can be proved by the experiment result shown in Fig. 10. The wave shape is observed clearly for the inhomogeneous deformation between neighboring grains.

Fig. 9 Distribution of logarithm strain (d 0.81 mm × 1.62 mm, DGO I, RH 0.2 mm)

Fig. 10 Effect of grain orientation on surface topography (d 0.81 mm ×1.62 mm)
With the same distribution of the grain orientation, the simulation is carried out with the specimen of d 1.16 mm × 1.62 mm, as shown in Fig. 11. An inhomogeneous deformation also appears clearly. However, the effect of inhomogeneous deformation on the surface topography becomes weaker. The height of every wave is measured from two specimen simulations shown in Fig. 12. With the decrease of specimen dimension, the height of wave becomes larger, which means that the effect of grain orientation increases with the decrease of specimen dimension.

Fig. 11 Distribution of logarithm strain (d1.16 mm × 1.62 mm, DGO I, RH 0.2 mm)
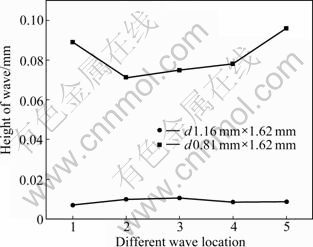
Fig. 12 Height of wave obtained from two specimens with different diameters
From the analysis of simulation results shown above, the inhomogeneous deformation is induced by different grain orientations. To investigate the effect in details, a new distribution of grain orientation is considered as follows. With the distribution DGO II, the simulation result is shown in Fig. 13. Compared with the result obtained with DGO I, the effect of the grain anisotropy becomes smaller because two neighboring grains have the same grain orientation.

Fig. 13 Distribution of logarithm strain (d 0.81 mm × 1.62 mm, DGO II, RH 0.2 mm)
In a real metal material, the orientation of every grain is different for the stochastic distribution. To investigate the effect of the grain orientation, the other grain orientation [111] is considered in the simulation model to study the effect of grain anisotropy in details. Three kinds of original grain orientations [001], [011] and [111] are assumed and arranged alternately, and the grain number of every grain orientation is the same (DGO III). The simulated logarithm strain is shown in Fig. 14. The anisotropy of grains leads to an obviously inhomogeneous deformation. It can be observed that grains with “soft orientation” are deformed easily, and the deformation of the grains with “hard orientation” becomes difficult. Between the “soft orientation” [011] and “hard orientation” [111] grains, there are transition grains [001], which can reduce the effect of grain anisotropy. This result clearly reveals the deformation character of microforming in theory analysis. When there are lots of grains in bulk materials, e.g., in macroforming, the effect of grain anisotropy can be decreased by the transition grains, and the homogeneous deformation can be obtained easily. However, there may be only several grains in micro specimen, and inhomogeneous deformation appears stochastically for the lack of transition grains. The microforming process shows the characteristics of poor reproducibility. So, it is difficult to completely simulate the microforming processes theoretically.
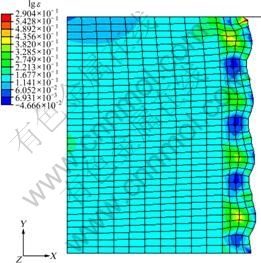
Fig. 14 Distribution of logarithm strain (d 0.81 mm × 1.62 mm, DGO III, RH 0.2 mm)
4 Conclusions
1) With the same grain size, an obvious decrease of flow stress is observed when the specimen is scaled down because the grains at free surface layer can be deformed easily.
2) The flow stress of specimen is changed by the change of grain orientation distribution, which leads to the scatter of flow stress. And its difference of different grain orientation distributions becomes smaller with the progress of plastic deformation for the grain orientation turning. The distribution of grain orientation has an obvious effect on the surface topography for the inhomogeneous deformation.
3) As for the existence of “hard orientation” grain, the inhomogeneous deformation becomes clearer. When two neighboring grains have the same grain orientation or a “hard orientation” grain is neighbored by a “soft orientation” grain, the effect of the grain anisotropy becomes weaker. The developed model based on crystal plasticity theory is effective in the analysis of the microforming processes.
References
[1] JESWIET J, GEIGER M, ENGEL U, KLEINER M, SCHIKORRA M, DUFLOU J, NEUGEBAUER R, BARIANI P, BRUSCHI S. Metal forming progress since 2000 [J]. CIRP J of Manu Sci Tech, 2008(1): 2-17.
[2] GEIGER M, KLEINER M, ECKSTEIN R, TIESLER N, ENGEL U. Microforming [J]. Ann of CIRP, 2001, 50: 445-462.
[3] MICHEL J F, PICART P. Size effects on constitutive behaviour for brass in sheet metal forming [J]. J Mater Process Tech, 2003, 141: 439-446.
[4] DIEHL A, ENGEL U, GEIGER M. Influence of microstructure on the mechanical properties and the forming behaviour of very thin metal foils [J]. Int J Adv Manuf Tech, 2010, 47: 53-61.
[5] SHEN Yu, YU Hu-ping, RUAN Xue-yu. Discussion and prediction on decreasing flow stress scale effect [J]. Transactions of Nonferrous Metals Society of China, 2006, 16: 132-136.
[6] CHAN W L, FU M W, LU J. The size effect on micro deformation behvavior in micro-scale plastic deformation [J]. Material Design, 2011, 32: 198-206.
[7] GEISSDORFER S, ENGEL U, GEIGER M. FE-simulation of microforming processes applying a mesoscopic model [J]. Int J Mach Tool Manu, 2006, 46: 1222-1226.
[8] GEISSDORFER S, ENGEL U, GEIGER M. Mesoscopic model-advanced simulation of microforming processes [J]. Production Engineering, 2007, 1(1): 79-84.
[9] GAU J T, PRINCIPE C, WANG J. An experimental study on size effects on flow stress and formability of aluminum and brass for microforming [J]. J Mater Process Tech, 2007, 184: 42-46.
[10] MAHABUNPHACHAI S, KOC M. Investigation of size effects on material behavior of thin sheet metals using hydraulic bulge testing at micro/meso-scales [J]. Int J Mach Tool Manu, 2008, 48: 1014-1029.
[11] YASIN H, ZBIB H M, KHALEEL M A. Size and boundary effects in discrete dislocation dynamics: Coupling with continuum finite element [J]. Mat Sci Eng A, 2001, 309-310: 294-299.
[12] HENNING M, VEHOFF H. Local mechanical behavior and slip band formation within grains of thin sheets [J]. Acta Mater, 2005, 53: 1285-1292.
[13] ASARO R J. Micromechanics of crystals and polycrystals [J]. Adv Appl Mech, 1983, 23: 1-115.
[14] PEIRCE D, ASARO R J, NEEDLEMAN A. Material rated dependence and localized deformation in crystalline solids [J]. Acta Metallurgica, 1983, 31: 1951-1976.
[15] BECKER R. Effects of strain localization on surface roughening during sheet forming [J]. Acta Mater, 1998, 46: 1385-1401.
晶体塑性模型分析微圆柱墩粗变形尺寸效应机理
程利冬1, 王振龙1, 2
1. 哈尔滨工业大学 机电工程学院, 哈尔滨 150001;
2. 哈尔滨工业大学 微系统与微结构制造教育部重点实验室, 哈尔滨 150001
摘 要:为了分析单个晶粒变形行为对微成形的影响,将自由表面的晶粒看作单晶体构建晶体塑性模型。基于率相关晶体塑性理论,考虑试样尺寸、初始晶体取向及其分布,分析微圆柱体墩粗变形中尺寸效应机理。结果表明,流动应力随着试样尺寸的减小而明显减小,晶体取向的分布对试样流动应力具有显著影响,并随着塑性变形的进行而减小。由于单晶体的各向异性,在试样表层发生了明显的非均匀变形,这将导致表面粗糙度的增加,小尺寸试样则更加明显。过渡晶粒的存在使得晶粒各向异性对表面形貌的影响减小。模拟结果得到了实验验证,这表明所建立的模型适合于以尺寸依赖性、流动应力分散性和非均匀变形为特点的微成形工艺分析。
关键词:微成形;尺寸效应;晶体塑性;晶体取向
(Edited by CHEN Wei-ping)
Foundation item: Project (50835002) supported by the National Natural Science Foundation of China; Project (QC08C55) supported by the Natural Science Foundation of Heilongjiang Province, China; Project (200802131031) supported by the PhD. Programs Foundation of Ministry of Education of China for Young Scholars
Corresponding author: CHENG Li-dong; Tel: +86-451-86417711-803, +86-18646649882; E-mail: ldchenghit@hit.edu.cn
DOI: 10.1016/S1003-6326(11)61483-0