J. Cent. South Univ. (2016) 23: 2110-2117
DOI: 10.1007/s11771-016-3267-x
Bending behaviour of lightweight aggregate concrete-filled steel tube spatial truss beam
FU Zhong-qiu(傅中秋)1, JI Bo-hai(吉伯海)1, ZHU Wei(朱伟)1, GE Han-bing(葛汉彬)1, 2
1. College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China;
2. Department of Civil Engineering, Meijo University, Nagoya, 468-8502, Japan
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: A lightweight aggregate concrete-filled steel tube (LACFST) spatial truss beam was tested under bending load. The performance was studied by the analysis of the beam deflection and strains in its chords and webs. According to the test results, several assumptions were made to deduce the bearing capacity calculation method based on the force balance of the whole section. An optimal dimension relationship for the truss beam chords was proposed and verified by finite element analysis. Results show that the LACFST spatial truss beam failed after excessive deflection. The strain distribution agreed with Bernoulli-Euler theoretical prediction. The truss beam flexural bearing capacity calculation results matched test evidence with only a 3% difference between the two. Finite element analyses with different chord dimensions show that the ultimate bearing capacity increases as the chord dimensions increase when the chords have a diameter smaller than optimal one; otherwise, it remains almost unchanged as the chord dimensions increase.
Key words: lightweight aggregate concrete-filled steel tube; spatial truss beam; bending behaviour; bearing capacity
1 Introduction
Similar to other types of composite structure, a concrete-filled steel tube (CFST) can take full advantage of the mechanical properties of both steel and concrete. It has a high bearing capacity, as well as being more economical compared with concrete alone [1-2]. Therefore, they are widely used in engineering projects [3-4]. Compared with a filling of normal concrete, filling with lightweight aggregate concrete (LAC) can save weight. Previous research has shown that lightweight aggregate concrete-filled steel tubes (LACFST) also have excellent mechanical performance, similar to that of a CFST [5-6]. CFSTs have already been used, not only for columns [7-8], but also for beams [9-10]: several types of composite beams, combining CFST with concrete decking have been studied [11-12]. For traditional space steel pipe truss beams, stability and local buckling thereof are the key problems influencing structural bearing capacity [13]. Concrete infill in the steel pipes of a truss beam is an effective way to improve stability and overcome local buckling problems, especially at positions with inevitable concentrations of force such as at nodes, bearings. If an LACFST is used, the span and capacity of spatial truss beams can increase.
The application of CFST truss beams, however, is not widespread. Nevertheless, there are five CFST space truss bridges which have been built in China: the Zidong Bridge in Guangdong, Xiangjiaba Bridge in Hubei, Wanzhou Bridge in Chongqing, Wan’ang Bridge in Chongqing, and the Ganhaizi Bridge in Sichuan. Of these bridges Zidong Bridge and Wan’ang Bridge are cable-stayed, while the others are beam bridges. During the construction of these bridges, static load tests and experimental studies were undertaken on their truss beams[14]: these tests on real bridges remained within the elastic stage which cannot reflect the non-linear behaviour and ultimate bearing capacity of the structure. In this work, an LACFST spatial truss beam was tested under bending load and the bending behaviour was studied.
2 Experimental investigation
2.1 Specimen
The specimen was designed with reference to the construction requirements of “The Chinese Code for the Design of Steel Structures (GB 50017—2003)”. The dimensions of the test specimen are shown in Fig. 1 and Table 1. The letters a to m in Fig. 1 represent the node number in the truss beam model. The straight welded steel tube was used in this test. The angle between the chord member and web member was θ = 42° in the side elevation. The angle between web members was ψ = 67° in the cross-sectional view. The minimum distance between web member surface was 42 mm at the same node.
Initially, all of the members were fabricated independently. Before welding, all members were fixed into position with their sections reversed. The axes of all members were aligned to ensure intersection at the centres of each node. Then, the upper chord,upper flat, and web members were welded together. At the same time, the bottom chord and bottom flat members were welded together. Then, the webs were filled with LAC. To ensure compaction during the pour, a vibrator was used outside of the web during concreting: seven days later, the webs were welded to the bottom chord. A circular plate (8 mm thick) was welded to one end of the chord member. After all the welding work, the specimen was set-up with the chords upright. LAC was poured into the chord members, layer-by-layer, and vibrated to ensure its density reached specification. Several node welding specimens were tested before the truss beam specimen verified weld quality.
2.2 Material properties
A group of three standard specimens were tested to determine the tensile strength of the steel. The specimens were cut from the steel tube and tested in accordance with Chinese Standard “Metallic materials at ambient temperature: tensile test method” (GB/T228—2002). The mechanical properties of the steel pipe are listed in Table 1. In accordance with relevant Chinese Standards; compression tests were carried out on a number of standard cubes (150 mm×150 mm×150 mm) and prisms (150 mm×150 mm×300 mm) to determine the 28-d compressive strength (fck) and elastic modulus (Ec) of the unconfined concrete. The concrete mix constituents and material properties are listed in Table 2.
2.3 Test instruments and procedure
Testing was carried out in the structural engineering laboratory of Hohai University. The load was provided by mechanical jack and applied to the specimen as shown in Fig. 1. It was applied on a steel beam which was simply supported on two other steel beams which were placed in the requisite loading positions. The load was measured by pressure sensor, and the strain was measured by strain gauges: four longitudinal, and two circumferential, strain gauges were disposed around each section. The longitudinal strain gauges (S1 to S4) were distributed uniformly around the steel pipe circumference. The circumferential strain gauges (S1′ to S3′) shared the same positions as S1 to S3. Several displacement meters (d1 (d1′) to d3 (d3′)) were distributed uniformly along the length to measure the deformation of the beam. Figure 1 shows the positions of the load and measurement points. All the instruments were attached to a data-processing system controlled by a personal computer.
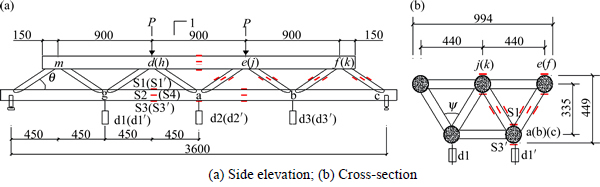
Fig. 1 Schematic diagram of specimen (Unit: mm):
Table 1 Mechanical properties of steel

Table 2 Mix proportion and mechanical properties of concrete

Staged loading was adopted during this test. From the node welding specimen tests, the ultimate load value was control by deformation. So, before 90% of the predicted ultimate load, the specimens were loaded at rate of one tenth of the predicted ultimate load at each step. Each load increment was held for two minutes to enable the development of all likely deformation thereat. Then, the specimens were loaded at rate of 5% of the predicted ultimate load per step. When approaching the predicted ultimate capacity, the load was added continuously, and slowly, until the deformation became apparent.
3 Experimental results
3.1 Failure mechanism
Figure 2 shows the load-deflection curve for the span at mid-section of the specimen. Initially, it is elastic (line OA). The curve is quasi-linear and the change of the gradient is not obvious. As the load increased, the specimen enters its elasto-plastic phase (line AC). The deflection increases rapidly: beyond point C, the deflection increases quickly while the bearing capacity undergoes practically no further increase. The curve has no falling branch at deflections of more than L/50. It can be seen that this trussed beam has good flexural bearing capacity and is ductile.
In this test, the specimen failed through excessive deflection. It had not reached its limiting bearing capacity. Although effective connections at nodes werethe controlling factor affecting its bearing capacity, the connections did not fail in this specimen. However, the welding slag falling off the nodes also indicated that the nodal connections were a key factor controlling the bearing capacity. None of the bar member bars underwent buckling: there was no slip between the steel tube and the concrete of any chord member. The bottom and upper chord members of the truss beam deformed consistently, indicating good ductility.
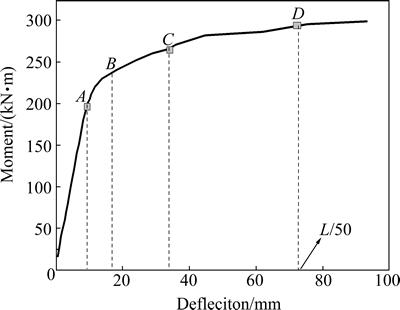
Fig. 2 Moment-deflection curve at mid-span
3.2 Deformation
Figure 4 shows the distribution of deflection along the span. The deflection increases symmetrically as the load increases: the deflection plots are of half-sine wave form.
Figure 5 shows the longitudinal strain distribution along the height at mid-span cross-section. From the material properties, the yield strain for this steel is about 1.8×10-3. For clarity, two figures are used to show the strain distribution in the elastic stage and thereafter. It is noticed that the strain distribution agrees with Bernoulli- Euler theory at various loading stages. Initially, the upper chords are under compression while the bottom chords are in tension. The tensile stress is present only in the steel of the two bottom chords while compression is present in the concrete and steel of all three upper chords. So, the neutral axis location moves up as the load increased. After the elastic stage, the neutral axis lies in the section of the upper chord, and the stress in the upper chord sections changes from compression to tension in their lower parts.
3.3 Strain in bars
Figure 6 shows the moment-average longitudinal strain curves for the web member. As shown, the strain in the web is relatively small compared to the yield strain which is 1.8×10-3. This indicates that the force in the web members is also relatively small. It also shows that the webs nearer the bearing are subjected to a larger axial force which is caused by the larger shear force.
Figure 7 shows the longitudinal load-strain curves for the chords. For the bottom chord (ga), the strain in the top side (S1) increases the quickest and that in the bottom side (S3) increases the least. All strains exceed the yield strain. The whole section of the bottom chord is in tension. For the upper chord (hj), the whole section is in compression at the beginning of the loading process. The strain in the top side (S1) increases quickest while the bottom one does so the least. Under increasing load, the top side of the upper chord section begins to yield and the bottom side strain changes from compressive to tensile.

Fig. 3 Failure of specimen:
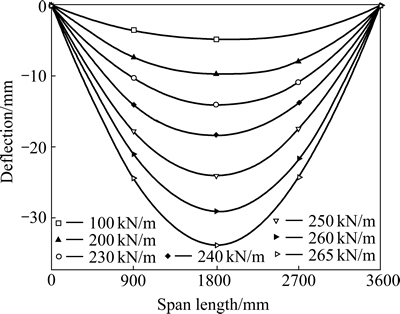
Fig. 4 Deflection distribution along span
3.4 Values from test results
The bottom side strain curve at the mid-span section of the bottom chord (position a in Fig. 1) is shown in Fig. 8. In this test, the specimen failed because of excessive deflection without a decrease in strain. So, the strain was used to decide the bearing capacity limit.
In this work, the moment was taken as the ultimate moment Mu when the strain was 0.01. The moment corresponding to a strain of 0.003 was taken as the yield moment My. From the strain data, the ultimate moment Mu was 267 kN/m and the yield moment My was 234 kN·m. Compared to the deflection curve (see Fig. 2), the values above were verified.
The flexural stiffness serviceability-level was taken as 0.6Mu [15]. As shown, the specimen was elastic at M=0.6Mu. So, the flexural stiffness value at the serviceability limit state was taken as B=35.67×103 kN/m2 in this test.
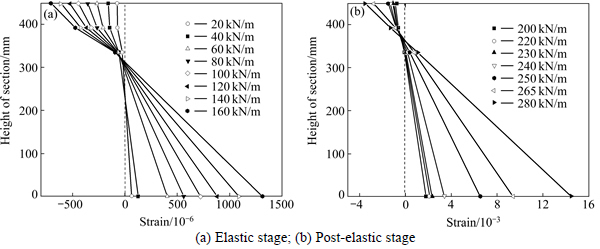
Fig. 5 Longitudinal strain distributions at mid-span:
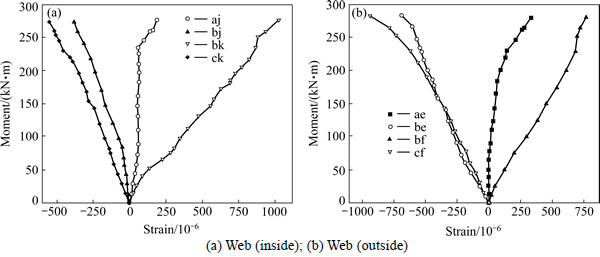
Fig. 6 Longitudinal strain in web members:
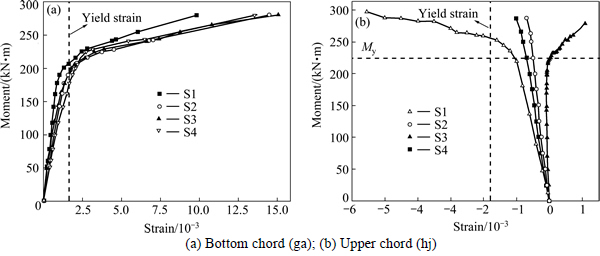
Fig. 7 Load-strain curves for chords:
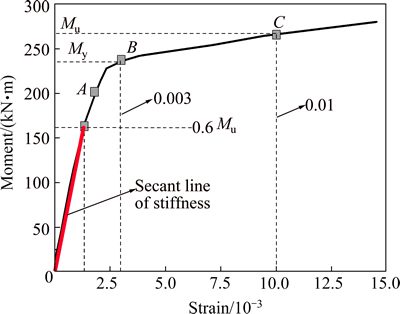
Fig. 8 Strain at mid-span section of bottom chords
4 Design calculation and suggestions
4.1 Bearing capacity
To calculate the bearing capacity, several assumptions were made based on the test results. Firstly, the strain distribution at a given cross-section agreed with Bernoulli-Euler theory. Secondly, the bearing capacity was controlled by the mid-span cross-section. Thirdly, only axial force was considered and any moment was ignored in the webs.
The position of the neutral axis should be confirmed by calculation. For the spatial truss beam tested here, the neutral axis occupies one of three positions, as shown in Fig. 9. Neutral axis 1 lies just under the upper chords; positions 2 and 3 are, respectively, above and below neutral axis 1. If the neutral axis is at position 1, there are three types of force in the section: T1 is the compressive force on the upper chords (steel and concrete together); T2 is the tensile force on the bottom chords without considering the contribution of the concrete; and T3 is the tensile force on the upper chords (Eqs. (1) to (3)):
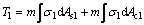 (1)
(1)
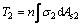 (2)
(2)
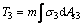 (3)
(3)
where σ1 is the compressive stress in the upper chords; σ2 and σ3 are the tensile stresses in the bottom and upper chords, respectively; As1 is the area of steel in compression in the upper chords; As2 and As3 are the areas of steel in tension in the lower and upper chords respectively, Ac1 is the area of concrete in compression in the upper chords, and m and n are the numbers of upper and lower chords.
The bearing moment can be found as
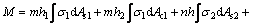
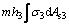 (4)
(4)
where h1 and h2 are the vertical distance from the neutral axis to the centroid of the upper chord compression steel and area of concrete, respectively; h and h3 are the vertical distances from the neutral axis to the centroid of the lower and upper chord tension steel, respectively.
In this test, the diameter of upper chords D1 and lower chords D2 were the same, and m>n. The neutral axis, therefore, lay in position 2. According to a balance of the forces acting upon the section, T1=T2+T3. Values of h3 were small and the stress on the bottom side of the upper chords was also small. So, T3 values were also deemed negligible. It can be thought that T3=0. From Fig. 7(a), all of the steel in the lower chord reached its yield strength fy. So, T2 can be calculated in Eq. (5) and the compressive area As1 and Ac1 can be found in Eq. (6):
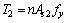 (5)
(5)
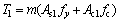 (6)
(6)
where fc is the combined strength of the LACFST (see Eq. (7) as proposed in Ref. [16]):
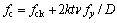 (7)
(7)
where k is a coefficient considering the constraining effect of the steel on the lightweight aggregate concrete. Based on previous research, k=3.4 [17], υ is the Poisson ratio of steel, t is the thickness of the steel, and D its external diameter.
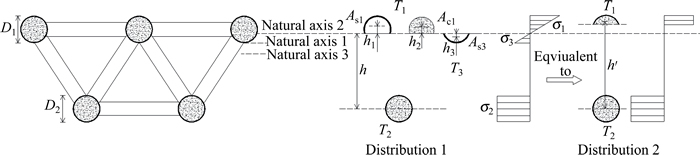
Fig. 9 Simplified diagram for bearing capacity calculation
From As1 and Ac1, the vertical dimension h′ from the compressive area centroid to the tension area centroid can be found. The bearing moment is given as
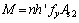 (8)
(8)
Thus, the ultimate bearing capacity can be calculated. The calculated result was 261 kN/m while the test result was 267 kN/m (less than 3% difference).
4.2 Design suggestion
For this test specimen, the neutral axis crossed the upper chord section when it reached ultimate bearing capacity. Part of the upper chord section remained unyielded. The material strength of the upper chords had not been fully mobilised. To make full use of the material strength, the material over the whole section was hoped to have been caused to yield.
If the upper chords has a different diameter from the lower chord, the neutral axis will lie in position 3 (beneath the bottom chord). The whole section of the upper chord will be compressed until it yields. According to the force balance across the section, it should meet the following conditions:
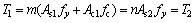 (9)
(9)
where As1 and Ac1 are the area of steel and concrete on one upper chord. The chords are dimensionally related as follows:
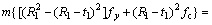
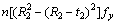 (10)
(10)
where R1 and R2 are the external radii of upper and lower chords, respectively; t1 and t2 are the thicknesses of the upper and lower chord steel tubes, respectively. If the dimensions of the chords match the relationship of Eq. (10), all of the material in the chords can be fully utilised. Under this condition, the dimensions are deemed optimal as proved in the following section by numerical analysis.
5 Numerical analysis
To explore the load-carrying performance of concrete-filled steel tube truss beams, a spatial finite element model was built using the bi-material non-linear finite element method. BEAM188 elements were adopted to build the model shown in Fig. 10. The joints connecting the web, rod, and chord member were set with the same nodes so as to transfer forces effectively. The constraints of the model were in accordance with experiment where translational freedoms in the UX-, UY-, and UZ-direction were constrained at one side (the fixed hinge support) while UY and UZ were constrained at another (the sliding hinge support).
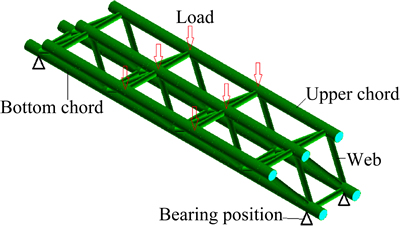
Fig. 10 FEM model
A bilinear kinematic (BKIN) model was adopted to establish the constitutive equation for the steel- pipe material. The concrete strength increases because of restraint from the surrounding steel pipe: this should be taken into consideration in this model. A constitutive model for confined concrete was built according to Eq. (7). Figure 11 shows the comparison of calculated and test results, where the conclusion may be drawn that the model results match that data obtained experimentally.
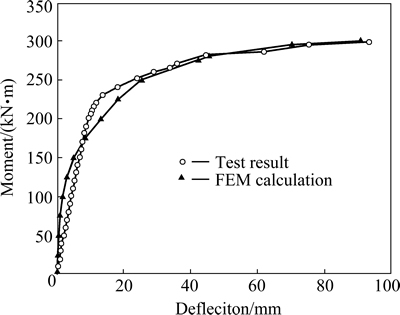
Fig. 11 FEM result
The most reasonable design dimensions of upper and lower chords were analysed and an optimal dimensional relationship between them was proposed (see Eq. (10)). Given this optimal dimension relationship, all of the chords in the concrete-filled steel tube truss girder fails at the same time and the whole system reaches its maximum bearing capacity. To prove the correctness of the optimal dimension relationship, the changes in bearing capacity were analysed. The ultimate bearing capacity for different dimensions of bottom chord was calculated by spatial FEM model with the same dimension of upper chords. Two types of bottom chords with outer diameters of 57 mm and 70 mm were considered. The dimensions of the web and the chord thicknesses were the same as that of the test specimen. The ultimate bearing capacity was found in the same way as used experimentally (see Table 3 and Fig. 12).
Table 3 and Fig. 12 show that the ultimate bearing capacity of the upper chords increases with increasing diameter within certain bounds (i.e. at less than the optimal dimension). However, the bearing capacity thereof remains stable when the optimal dimension is reached.
The change in bearing capacity for different upper chord dimensions can be seen in Fig. 13. The optimal diameter of the upper chord is 24 mm when the diameter of the bottom chord is 57 mm. At its optimal dimensions, the ultimate bearing capacity of this truss girder is 292.8 kN/m. The bearing capacity increases as the upper chord diameter increases when its outside diameter is less than the optimal diameter of 24 mm. The bearing capacity remains practically constant as the diameter of upper chords increases beyond 24 mm. A similar trend in the bearing capacity occurs when the outside diameter of the bottom chords is 70 mm. This proves the accuracy of the proposed optimal dimensions for the truss beam chords.
Table 3 Calculation results of ultimate bearing capacity
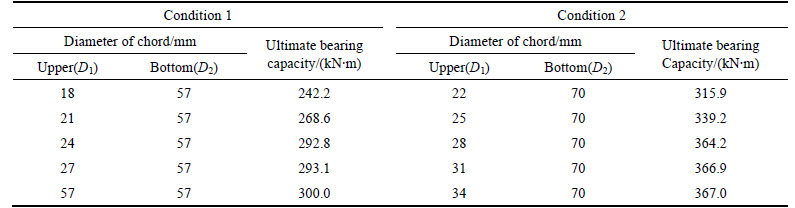
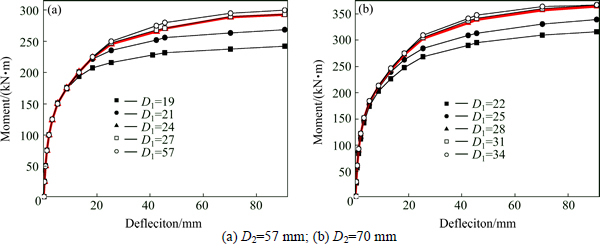
Fig. 12 Bearing capacity calculation results:
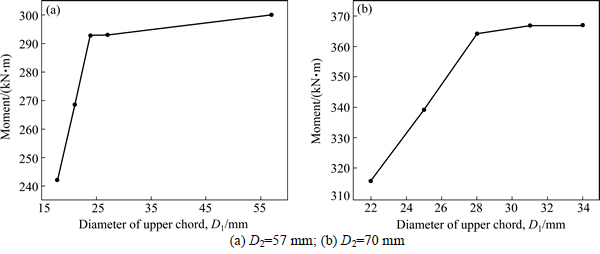
Fig. 13 Ultimate bearing capacity:
6 Conclusions
1) In this test, the lightweight aggregate concrete-filled steel tube spatial truss beam failed through excessive deflection under flexural load. The deflection curves are of half-sine wave form and the strain distribution matched Bernoulli-Euler theory at various loading stages.
2) At the mid-span, the whole section of the bottom chord underwent tensile yield, while the upper chords failed with part of their section undergoing compressive yield. The web members are subjected to little force herein. The structure is ductile and exhibited good overall spatial performance.
3) According to test results, the calculation method of truss beam flexural bearing capacity is deduced based on the assumption of all materials reaching their bearing strengths. The calculated results agree with the experimental data with only 3% difference observed between them.
4) Considering the most reasonable position of the neutral axis and the force balance across the whole section, an optimal dimensional relationship between the truss beam chords is proposed. The FEM calculation of the truss beam bearing capacity with different chord dimensions proves the correctness of this optimal dimension relationship.
References
[1] GULER S, COPUR A, AYDOGAN M A. Comparative study on square and circular high strength concrete-filled steel tube columns [J]. Advanced Steel Construction, 2014, 10(2): 234-247.
[2] XIAO Jian-zhuang, HUANG Yi-jie, SUN Zhi-hui. Seismic behavior of recycled aggregate concrete filled steel and glass fiber reinforced plastic tube columns [J]. Advances in Structural Engineering, 2014, 17(5): 693-707.
[3] YUAN Hui-hui, DANG Ji, TETSUHIKO A. Behavior of partially concrete-filled steel tube bridge piers under bi-directional seismic excitations [J]. Journal of Constructional Steel Research, 2014, 93: 44-54.
[4] ROEDER C W, LEHMAN D E, STEPHENS M. Concrete-filled steel tubes for accelerated bridge construction [J]. Transportation Research Record, 2014, 2406: 49-58.
[5] MOULI M, KHELAFI H. Strength of short composite rectangular hollow section columns filled with lightweight aggregate concrete [J]. Engineering Structures, 2007, 29(8): 1791-1797.
[6] ELZIEN A, JI Bo-hai, FU Zhong-qiu, HU Zheng-qing. Behavior of lightweight aggregate concrete filled steel tube columns under eccentric loading [J]. Steel and Composite Structures, 2011, 11(6): 469-488.
[7] CHEN Zong-ping, XU Jin-jun, XUE Jian-yang, SU Yi-sheng. Performance and calculations of recycled aggregate concrete-filled steel tubular (RACFST) short columns under axial compression [J]. International Journal of Steel Structures, 2014, 14(1): 31-42.
[8] MOHAMMAD Y, BRIAN U, ZHONG Tao, REMENNIKOV A, RICHARD J Y. Impact behaviour of pre-compressed hollow and concrete filled mild and stainless steel columns [J]. Journal of Constructional Steel Research, 2014, 96: 54-68.
[9] NAKAMURA S, MOMIYAMA Y, HOSAKA T, HOMMA K. New Technologies of steel/concrete composite bridges [J]. Journal of Constructional Steel Research, 2002, 58(1): 99-130.
[10] KANG J Y, CHOI E S, CHIN W J. Flexural behavior of concrete-filled steel tube members and its application [J]. International Journal of Steel Structures,2007, 7(4): 319-324.
[11] MOSSAHEBI N, YAKEL A, AZIZINAMINI A. Experimental investigation of a bridge girder made of steel tube filled with concrete [J]. Journal of Constructional Steel Research, 2005, 61(3): 371-386.
[12] YANG You-fu, MA Guo-liang. Experimental behaviour of recycled aggregate concrete filled stainless steel tube stub columns and beams [J]. Thin-Walled Structures, 2013, 66: 62-75.
[13] LIU Su, MICHAEL B F, ZHOU Wen-xing. Alternative load paths in steel through-truss bridges: Case study [J]. Journal of Bridge Engineering, 2013, 18: 920-928.
[14] ZHANG Lian-yan, LI Ze-sheng, CHENG Mao-fang. Concrete filled steel tube space truss composite beam structure [M]. Beijing: China Communications Press, 1999. (in Chinese)
[15] HAN Lin-hai, LIAO Fei-yu, TAO Zhong, HONG Zhe. Performance of concrete filled steel tube reinforced concrete columns subjected to cyclic bending [J]. Journal of Constructional Steel Research,2009, 65(8): 1607-1616.
[16] FU Zhong-qiu, JI Bo-hai, MAENO H, ElZIEN A, CHEN Jia-shu. Flexural behavior of lightweight aggregate concrete filled steel tube [J]. Advanced Steel Construction, 2014, 10(4): 385-403.
[17] FU Zhong-qiu, JI Bo-hai, YU Zheng-peng, YANG Ming. Combined strength of lightweight aggregate concrete-filled steel tube [J]. Materials Research Innovations, 2015, 19(S5): 898-901.
(Edited by DENG Lü-xiang)
Foundation item: Project(51208176) supported by the National Natural Science Foundation of China; Projects (2012M511187, 2013T60493) supported by the China Postdoctoral Science Foundation; Project(2015B17414) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2015-04-20; Accepted date: 2015-09-21
Corresponding author: FU Zhong-qiu, Associate Professor, PhD; Tel: +86-13585184077; E-mail: fumidaut@163.com