A practical nonlinear controller for levitation system with magnetic flux feedback
来源期刊:中南大学学报(英文版)2016年第7期
论文作者:李杰 李金辉
文章页码:1729 - 1739
Key words:maglev; levitation system; backstepping; magnetic flux
Abstract: This work proposes a practical nonlinear controller for the MIMO levitation system. Firstly, the mathematical model of levitation modules is developed and the advantages of the control scheme with magnetic flux feedback are analyzed when compared with the current feedback. Then, a backstepping controller with magnetic flux feedback based on the mathematical model of levitation module is developed. To obtain magnetic flux signals for full-size maglev system, a physical method with induction coils installed to winding of the electromagnet is developed. Furthermore, to avoid its hardware addition, a novel conception of virtual magnetic flux feedback is proposed. To demonstrate the feasibility of the proposed controller, the nonlinear dynamic model of full-size maglev train with quintessential details is developed. Based on the nonlinear model, the numerical comparisons and related experimental validations are carried out. Finally, results illustrating closed-loop performance are provided.
J. Cent. South Univ. (2016) 23: 1729-1739
DOI: 10.1007/s11771-016-3227-5
LI Jin-hui(李金辉)1, 2, LI Jie(李杰)1
1. College of Mechatronics Engineering and Automation, National University of Defense Technology,Changsha 410073, China;
2. The First Engineers Scientific Research Institute of the General Armaments Department, Wuxi 214035, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: This work proposes a practical nonlinear controller for the MIMO levitation system. Firstly, the mathematical model of levitation modules is developed and the advantages of the control scheme with magnetic flux feedback are analyzed when compared with the current feedback. Then, a backstepping controller with magnetic flux feedback based on the mathematical model of levitation module is developed. To obtain magnetic flux signals for full-size maglev system, a physical method with induction coils installed to winding of the electromagnet is developed. Furthermore, to avoid its hardware addition, a novel conception of virtual magnetic flux feedback is proposed. To demonstrate the feasibility of the proposed controller, the nonlinear dynamic model of full-size maglev train with quintessential details is developed. Based on the nonlinear model, the numerical comparisons and related experimental validations are carried out. Finally, results illustrating closed-loop performance are provided.
Key words: maglev; levitation system; backstepping; magnetic flux
1 Introduction
Compared with the conventional rail-way systems, the electromagnetic maglev system (EMS) has advantages of lower noise, less exhaust fumes emission, less maintenance cost, which is a new kind of urban transport that has been widely concerned in recent years [1-3].
The EMS maglev system uses attractive electromagnetic force to neutralize its gravity. The electromagnetic force produced by a constant current is inversely proportional to the square of the levitation gap, which makes the levitation system inherently unstable. Hence, an active controller to stabilize the levitation system is indispensable. Recently, extensive studies are carried out to achieve more satisfactory specifications [4-6].
In maglev engineering, the cascaded-loop control architecture with levitation gap and current feedbacks is widely adopted to control the electromagnetic force [7-8]. However, the electromagnetic force is inversely proportional to the square of the levitation gap, and positively proportional to the square of the current. To a certain extent, the relationships among the electromagnetic force, the levitation gap and current are interactive and complicated. It results in more difficulties for the synthesis and the performance improvement of the levitation system.
As we all known, the electromagnetic force is determined solely by the magnetic flux of the levitation clearances [9]. The relationship among the electromagnetic force, levitation gap and flux may be simple and clearer if the feedback of magnetic flux is adopted by the inner loop. In this way, the synthesis of the levitation system will be easier. To show the advantage of the control scheme, the theoretical analysis will be carried out in this work.
To stabilize the levitation system, the feedback of magnetic flux was reported in Ref. [10]. The experiments are carried on small SISO prototypes and the signal of magnetic flux is obtained by a Hall-effect element. For the full-size maglev system, the magnetic flux is up to 1.2 T.While the measuring range of the commercial Hall-effect sensor is less than 0.5 T. Hence, there are no suitable commercial flux transducers for full-size maglev system.
To tackle this problem, an induction method by coils attached to the windings of the electromagnet is proposed, and the effectiveness is checked by experiments. However, this acquisition method refers to the hardware installation of the coils and AD sampling circuits, which may go against its large-scale engineering applications. To avoid this issue, a novel conception of virtual flux acquisition method is proposed and its validity will be checked by numerical simulations and experiments in this work.
This study is engineering-oriented, and the purpose is to develop a practical backstepping control scheme that is capable of solving the inherent nonlinearity, dynamic coupling.
2 System modeling
The low-speed maglev vehicle CMS04 is partly shown in Figs. 1 and 2. The train consists of five bogies, and each bogie is made up of two levitation modules, which are connected by four anti-roll beams. Furthermore, a levitation module includes four electromagnets, and two adjacent electromagnets are driven by a suit of IGBT circuit and appointed as a fundamental unit.

Fig. 1 View of maglev system
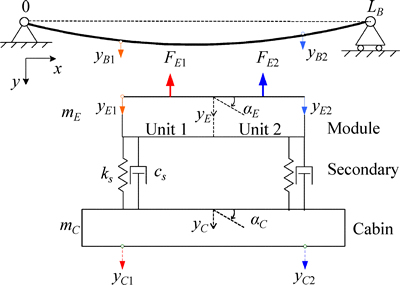
Fig. 2 Minimum model with a module, secondary and cabin
Considering the complexity of maglev system, an overall mathematical model with prominent details may result in a complicated analysis to obtain useful conclusions. Therefore, a suitable-scale model containing quintessential parts should be developed.
For the Old Dominion University maglev test system, a centralized approach at a bogie level is adopted [11]. They believed that the centralized control at a bogie level is more capable of lateral displacements suppression.
In Ref. [12], the dynamic coupling between the two adjacent fundamental units and the misalignment between the actuators and sensors are neglected. Furthermore, the mathematical model and controller at a fundamental unit level are developed. However, the engineering running tests indicate that this control scheme can not tackle influence of the dynamic coupling and misalignment.
Hence, a mathematical model including the coupling and misalignment should be developed. For the CMS04 maglev system, the two levitation modules of a bogie are almost independent due to the flexible connection of anti-roll beams. The centralized control at a bogie level could be degraded to the decentralized control at a module level, as shown in Fig. 2. In this way, the quintessential parts, including the nonlinear behavior of electromagnetic force, the dynamic coupling and misalignment, will be all included and managed.
According to Fig. 2, the levitation gaps measured by the gap sensor are
 (1)
(1)
However, for the levitation system, the averaged electric clearance  between the upper surface of the electromagnets and the lower surface of the guide-way is
between the upper surface of the electromagnets and the lower surface of the guide-way is
 (2)
(2)
Suppose that the turn of a single electromagnet is N, its resistance is R, the pole area is A and the magnetic permeability of vacuum is μ0. Then, for a single electromagnet the relationships between the control voltage ui(t) and current ii(t) are [1]:
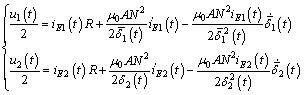 (3)
(3)
The electromagnetic forces acting on the bridge are [2]:
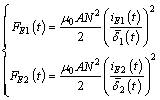 (4)
(4)
In light of Eq. (3), the relationships among the control voltage ui(t), the current iEi(t), the averaged electric clearance 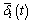 and its derivative
and its derivative 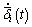 are complicated. Besides, the value of electromagnetic force
are complicated. Besides, the value of electromagnetic force 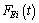 refers to two variables, the fluctuation of current
refers to two variables, the fluctuation of current 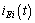 and averaged electric clearance
and averaged electric clearance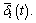 The synthesis of the levitation system based on the two complicated relationships is inconvenient.
The synthesis of the levitation system based on the two complicated relationships is inconvenient.
To simplify the above relationships, the magnetic flux Bi(t) instead of the current iEi(t) is adopted to develop the dynamic equations. In this way, Eq. (3) may be updated as
 (5)
(5)
The electromagnetic forces acting on the bridge may be updated as
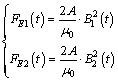 (6)
(6)
Compared with Eqs. (3) and (4), Eqs. (5) and (6) are seen to be much simpler. It may be favorable for the performance improvement of levitation system. The simpler and clearer relationships will be adopted in this work.
When the vehicle is suspended on bridges without moving, the forces acting on the module include the gravity, the pressures from the distortion of the air- springs and the electromagnetic forces. The dynamic equations of the levitation module are given as
 (7)
(7)
where △CE1=yE1- yC1-△CE0, △CE2= yE2-yC2-△CE0.
The forces acting on the cabin of train include its gravity and the counteracting force from the distortion of the air-springs. The dynamic equations of the cabin are given as
 (8)
(8)
3 Design of nonlinear levitation controller
Considering the essence of instability and limited fluctuation range (±3 mm) of levitation gaps, the clash between the electromagnets and the guide-way may occur if the time span of an unsuitable control scheme is longer than 20 ms. The clash may lead to the failure of levitation system, even damages of physical structures, which are unacceptable for the commercial application of maglev system. Hence, a control algorithm with a systematic procedure and the corresponding feedback control laws which guarantee the stability of the related system is expected.
The backstepping is a systematic and recursive design methodology for nonlinear feedback control, which is originally proposed for complex strict-feedback. With the development of backstepping control, this method has been widely applied in SISO affine systems [13-14]. Recently, the combination between the backstepping control and fuzzy control has been reported [15-16].
The idea of backstepping design is to select some appropriate functions of state variables as virtual control variables for lower dimension subsystems of the overall system recursively. When the procedure terminates, the final control scheme guarantees the stability by virtue of the total Lyapunov function, which is formed by summing up the Lyapunov functions associated with each individual design stage [18-20].
In Ref. [21], an adaptive backstepping control scheme was proposed to control the mover position of a magnetic SISO levitation apparatus. They believed that excellent transient performance is held. To some extent, the backstepping control is viewed as one of the innovative nonlinear control methods and preferred in this study to stabilize the MIMO levitation system.
Compared with the movement of the electromagnet, the movement of cabin is much slower and smaller due to the low pass attribute of air springs. Hence, the deformation of air springs is mainly determined by the movement of electromagnet. Besides, the movement of cabin is immeasurable. We have no option but to suppose that the displacement of cabin yCi is static during the design process of controller. When the pulling motor accelerates or decelerates, the normal force impacts the levitation system.
Considering that the disturbance from cabin and pulling motor is low-frequency, its influence could be compensated by integral terms. For convenience, the above disturbance will not be considered temporarily. Then, the mathematical model of system can be written as
 (9)
(9)
where the vector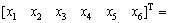
 y1r and y2r are the inertial coordinates of trajectory; △1r and △2r are the desired levitation gaps between the vertical displacements of electromagnet yEi and trajectory yir. Due to the lack of the information when designing the controller, the inertial coordinates of the trajectory and desired gaps are assumed to be constant. Defining
y1r and y2r are the inertial coordinates of trajectory; △1r and △2r are the desired levitation gaps between the vertical displacements of electromagnet yEi and trajectory yir. Due to the lack of the information when designing the controller, the inertial coordinates of the trajectory and desired gaps are assumed to be constant. Defining
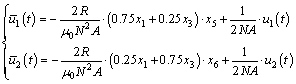 (10)
(10)
To decompose the MIMO system (9) into two SISO subsystems for the design simplification of backstepping controller, four intermediate variables, x7, x8 and v1, v2 are denoted as
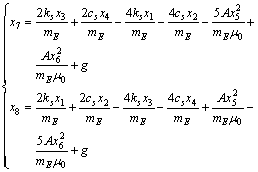 (11)
(11)
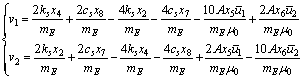 (12)
(12)
After mathematical derivation, the MIMO system (9) is degraded into two parallel SISO subsystems as follows:
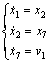 (13)
(13)
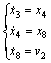 (14)
(14)
Considering the symmetry properties between Eqs. (13) and (14), the control scheme of the subsystem (13) is considered firstly.Consider x2 as the first virtual control and x1 as the variable to be regulated. When the virtual control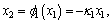 the dynamics of variable x1 is
the dynamics of variable x1 is Then, we construct the following Lyapunov function as
Then, we construct the following Lyapunov function as
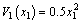 (15)
(15)
Its derivative is
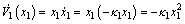 (16)
(16)
Obviously, 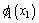 makes the time derivative of the Lyapunov function V1 negative definite on condition that the parameter
makes the time derivative of the Lyapunov function V1 negative definite on condition that the parameter 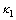 is positive. Hence, the equilibrium point
is positive. Hence, the equilibrium point 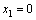 is asymptotically stable. The error between the virtual control variable x2 and
is asymptotically stable. The error between the virtual control variable x2 and 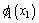 is defined as
is defined as 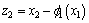 , then Eq. (13) can be arranged as
, then Eq. (13) can be arranged as
 (17)
(17)
Considering x7 as the second virtual control variable and z2 being the variable to be regulated, we construct the second augmented Lyapunov function V2 as
 (18)
(18)
Then, its derivative is
 (19)
(19)
When the second virtual control variable x7=  then the time derivative of the Lyapunov function V2 along the system trajectories is negative definite for given κ1>0 and κ2>0. Therefore, the equilibrium point of system Eq. (17) is asymptotically stable. Furthermore, the error between the virtual controls variables x7 and
then the time derivative of the Lyapunov function V2 along the system trajectories is negative definite for given κ1>0 and κ2>0. Therefore, the equilibrium point of system Eq. (17) is asymptotically stable. Furthermore, the error between the virtual controls variables x7 and  is defined as
is defined as
 (20)
(20)
Then Eq. (13) can be arranged as
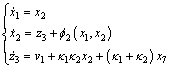 (21)
(21)
Considering v1 as the control variable and z3 being the variable to be regulated. We construct the third augmented Lyapunov function V3 as
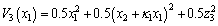 (22)
(22)
Then, its derivative is
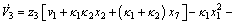
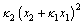 (23)
(23)
When the control variable 
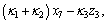 then its time derivative of the Lyapunov function V3 along the system trajectories is negative definite for given κ1>0, κ2>0 and κ3>0. Therefore, the equilibrium point of Eq. (13) is asymptotically stable. In light of Eq. (11), the control variable is
then its time derivative of the Lyapunov function V3 along the system trajectories is negative definite for given κ1>0, κ2>0 and κ3>0. Therefore, the equilibrium point of Eq. (13) is asymptotically stable. In light of Eq. (11), the control variable is
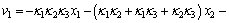
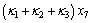 (24)
(24)
Furthermore, combining with Eq. (12), it gives

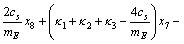
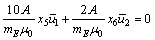 (25)
(25)
Similarly, based on the subsystem Eq. (14), it gives


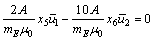 (26)
(26)
Combining Eqs. (25), (26) and (10), the control voltages of the system are
 (27)
(27)
where 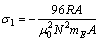 and
and 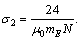 The control voltages u1(t) and u2(t) make the tracking errors decay to zero with the passage of time.
The control voltages u1(t) and u2(t) make the tracking errors decay to zero with the passage of time.
4 Signal acquisition about magnetic flux
In light of Eq. (27), the control voltages u1(t) and u2(t) are related with the feedback of levitation gaps x1 and x3, velocities 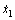 and
and 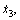 the accelerations
the accelerations and
and 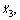 the magnetic flux B1 and B2. For the maglev engineering, the signals of levitation gaps x1 and x3, the accelerations
the magnetic flux B1 and B2. For the maglev engineering, the signals of levitation gaps x1 and x3, the accelerations  and
and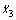 can are detected by the gap sensors and acceleration conductors, the velocities
can are detected by the gap sensors and acceleration conductors, the velocities 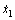 and
and  can be obtained by the integration of the corresponding acceleration. However, the signal of magnetic flux should be estimated properly due to unavailable sensors. Considering the limited measurement range of Hall-effect sensor and complicated working condition, it is unavailable for full- scale maglev system.
can be obtained by the integration of the corresponding acceleration. However, the signal of magnetic flux should be estimated properly due to unavailable sensors. Considering the limited measurement range of Hall-effect sensor and complicated working condition, it is unavailable for full- scale maglev system.
Luckily, according to Faraday’s law, the induction voltage is proportional to the derivative of the magnetic flux through a constant area. Therefore, coils attached to the winding of the electromagnets may be used to obtain the derivation of the magnetic flux. After integration and AD sampling, the signal of magnetic flux will be available for feedback. This technology shown in Fig. 3 is adopted in this work.

Fig. 3 Measurement of magnetic flux by induction coils
However, as for the induction coils, its structural strength, its water and thermal prevention are troublesome for engineering application. Besides, the signal isolation and AD sampling circuit are indispensable.
To avoid aforementioned issues, a novel technique of virtual acquisition method free from coils and AD sampling circuit is developed here. In light of the derivative of the magnetic flux in Eq. (5), it is rewritten as
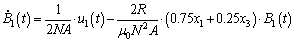 (28)
(28)
According to Eq. (28), the magnetic flux B may be obtained, providing that the variables u1(t), x1(t) and x3(t) are available. As we all known, the control voltage u1(t) is available according to Eq. (27), and the variables x1(t) and x3(t) is measurable. Theoretically, the flux signal B can be obtained by the integration of right teams of Eq. (28).
However, the gap sensor works in high electromagnetic environment. The measured values of levitation gap are polluted seriously. Secondly, the gap sensor is a “point” sensor. The measured levitation gaps are different from the averaged electric clearances.
Besides, when the maglev vehicle slips across the joints of the guide-way, the detection anomaly of the gap sensors may lead to the estimation of the flux unavailable.
In light of the relationship among the current, levitation gap and magnetic flux is as follows:
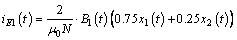 (29)
(29)
Substituting Eq. (29) into Eq. (28), it gives
 (30)
(30)
The current sensor is installed at the inner of the maglev controller box, which is free from magnetic noise pollution. Its signal quality is excellent. Besides, the current signal measured by the current sensor is free from the joints of the guide-way, and avoids the difference between the measured levitation gap and the averaged electric clearances. Hence, it can be used in Eq. (30) to obtain the flux B1(t) by the integration of right teams of Eq. (30).
In a real maglev system, measurements of current iE1(t) are polluted by its inexact direct bias and ultra low frequency disturbance, which will lead to integral saturation. Hence, the following estimator instead of ideal integrator is adopted.
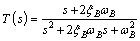 (31)
(31)
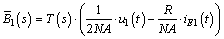 (32)
(32)
where ξB is the damping ratio of the estimator; ωB is the corner frequency and 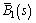 is the estimated value of magnetic flux.
is the estimated value of magnetic flux.
5 Numerical simulations
In this section, numerical simulations have been performed to demonstrate its feasibility. To improve the credibility of results, the nonlinear model with quintessential details is adopted in this section.
5.1 Comparative study with full states feedback controller
To make a comparative study between the proposed MIMO backstepping control with magnetic flux feedback and conventional SISO full states feedback control with current inner loop (also named PIDA controller in maglev engineering), the engineering widely used full states feedback controller is adopted.
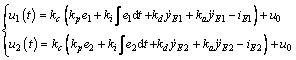 (33)
(33)
where 
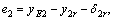 kp, ki, kd and kc are the well-tuned parameters of full states feedback controller by trial and error. The variable u0 is the steady control voltage of coils.
kp, ki, kd and kc are the well-tuned parameters of full states feedback controller by trial and error. The variable u0 is the steady control voltage of coils.
Firstly, the desired levitation gap △1r is set as a (9±2) mm square wave, and the desired levitation gap △2r is set as 9 mm without variation. When the desired levitation gap △1r is varied, the control voltage drives the levitation gap errors to decay to zero with the passage of time. In this process, its transient responses, including the overshoot and coupling vibration of the other levitation unit are the marker of the performance specifications of the levitation system. Generally, the less overshoot of the first fundamental unit and the less vibration of the second fundamental unit are expected.
In light of Fig. 4(a), for the first levitation unit, it can be seen that the overshoots is up to 2.47 mm for the full states feedback control scheme and 0.65 mm for the backstepping control scheme. It indicates that the trackability of the backstepping controller outperforms the full states feedback controller. The inferior performance of full states feedback control system mainly results from the nonlinear component of the voltage equation.
In light of Fig. 4(b), for the second levitation unit, the vibration of the second levitation unit is expected to be tiny. However, due to the interaction between the two levitation units, the fluctuation of levitation gap △E2 is up to 1.08 mm (full states feedback control system), which is much greater than 0.08 mm (module backstepping control system). Besides, according to Figs. 4(c) and (d), the amplitude of the current fluctuation is less when the module backstepping control scheme is adopted. It indicates that decoupling ability of the backstepping control system is better than the traditional full states feedback control system.
5.2 Comparative study between virtual magnetic flux and ideal flux feedback
In previous subsection, the advantages of the backstepping control system with magnetic flux, including the trackability and decoupling ability, are checked. However, the signal acquisition of the magnetic flux is not considered.
The induction method is effective for the signal acquisition of the magnetic flux. However, the installation of the coil, including its structural strength, its water and thermal prevention is troublesome. Besides, the signal isolation of the induction voltage and the circuit of AD sampling are indispensable. To avoid the issues, the effectiveness of the proposed virtual magnetic flux should be checked intensively.
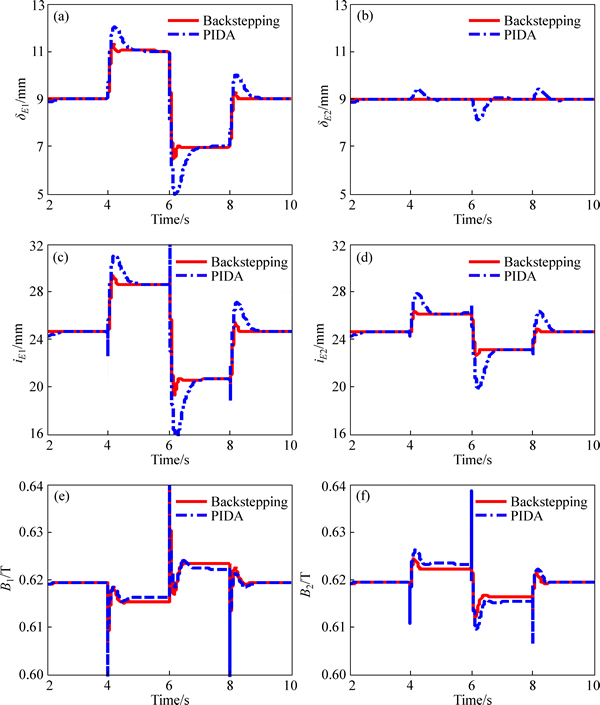
Fig. 4 Performance comparisons between backstepping controller and full states feedback controller
To check the validity of the virtual magnetic flux, the tracking performances of MIMO backstepping control system with ideal magnetic flux and virtual magnetic flux are shown in Fig. 5 individually. It can be seen that a high consistency of the tracking performance is held according to Figs. 5(a)-(d). Furthermore, according to Figs. 5(e)-(f), a high consistency of two kinds of magnetic flux signals is held in high-frequency ranges. However, the difference between the aforementioned twp kinds of magnetic flux signals is obvious in low-frequency ranges. The differences result from the estimator Eq. (32) instead of ideal integrator.
Luckily, the difference in low-frequency ranges is compensated by the integral term of control scheme. Hence, the numerical simulation verifies the effectiveness of the virtual magnetic flux feedback.
6 Experimental validations
To physically demonstrate the validity of the proposed control scheme, two following experiments are carried out on a single levitation bogie apparatus, as shown in Fig. 6.
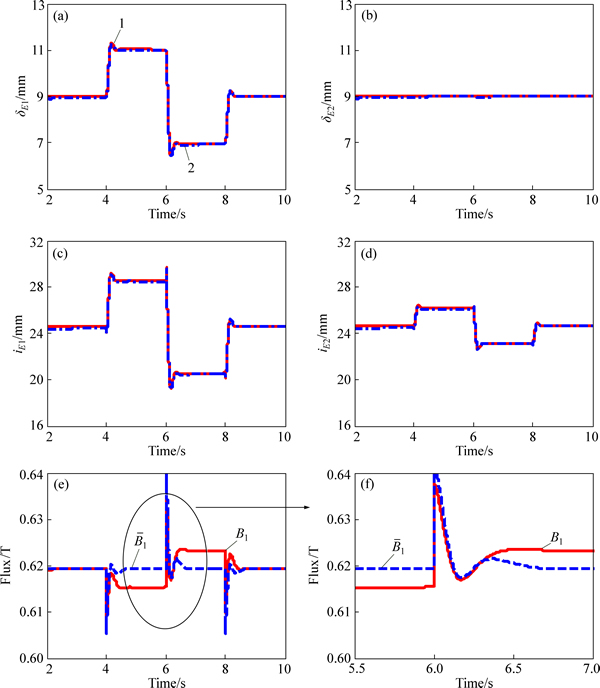
Fig. 5 Performance comparisons when ideal magnetic flux (B1, B2) and virtual magnetic flux  are adopted individually (1-Ideal magnetic flux feedback; 2-Virtual magnetic flux feedback)
are adopted individually (1-Ideal magnetic flux feedback; 2-Virtual magnetic flux feedback)

 Fig. 6 Experimental apparatus of a single levitation bogie
Fig. 6 Experimental apparatus of a single levitation bogie
To check the validity of induction method experimentally, induction coils with ten laps as shown in Fig. 6 are attached to the windings of the electromagnet. According to Faraday’s Law, the induction voltage of coils is proportional to the derivation of the magnetic flux. After integration and AD sampling, the signal of magnetic flux is detected by levitation controller.
The transient response of the MIMO backstepping control system with the feedback of magnetic flux obtained by induction method is shown in Figs. 7(a)-(b). It can be seen that the overshoot of △E1 is about 0.24 mm, and the rising time is about 0.2 s. Hence, the tracking performance of the proposed control scheme is excellent. Besides, the maximum fluctuation of △E2 is 0.26 mm, which indicates its excellent decoupling ability. Besides, according to Figs. 7(c) and (d), its minor amplitude of the current fluctuation is beneficial for the design of the power system.
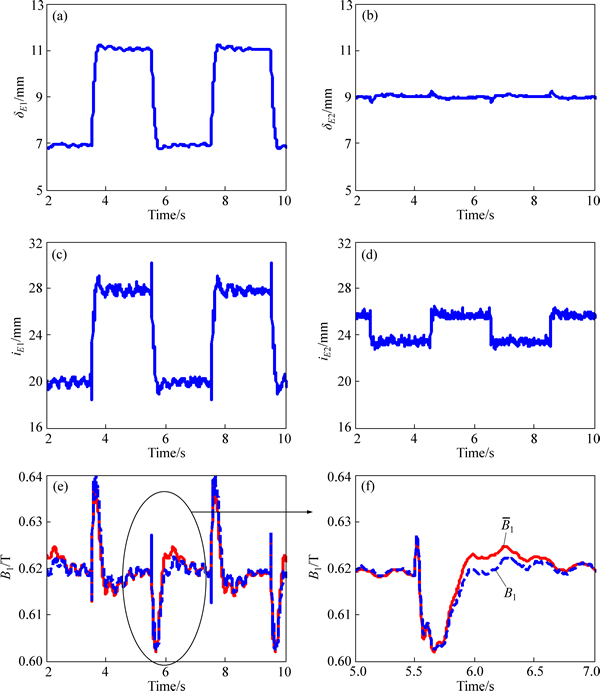
Fig. 7 Performance of module backstepping control system with feedback of physical flux signal B1
In light of Figs. 7(e)-(f), the difference between the physical flux and virtual flux signals is so tiny that it can be neglected, which reveals a considerable successful possibility that the virtual flux signals may replace the physical flux signals in engineering practice. In this way, the levitation system with magnetic flux feedback will be free from the induction coils and AD sampling circuit.
The transient response with virtual magnetic flux feedback is shown in Figs. 8(a)-(b). It can be seen that an identical trackability and decoupling ability have been achieved. Besides, according to Figs. 8(c) and (f), the fluctuation of the current and magnetic flux is satisfied. Hence,the validity of the virtual magnetic flux feedback has been checked by the single bogie apparatus.
7 Conclusions
1) The mathematical model of levitation modules is developed, and the advantages of magnetic flux feedback are analyzed when compared with the traditional cascaded-loop control with current feedback. The conclusion indicates that the dynamic behavior of the levitation system will be simpler when the magnetic flux feedback is adopted.
2) A nonlinear backstepping controller with magnetic flux feedback based on the mathematical model of levitation module is developed, which is capable of tackling the nonlinear and coupling characteristic of the levitation system.
3) The signals of the magnetic flux are discussed.
To satisfy the engineering acquirement, the induction method is developed. To avoid its hardware addition and cost, a novel conception of virtual magnetic flux feedback is proposed.
4) The nonlinear dynamic model of full-size maglev train with quintessential details is developed. Based on the nonlinear model, the numerical comparisons and related experimental validations are carried out and results illustrating closed-loop performance with virtual magnetic flux feedback are provided.
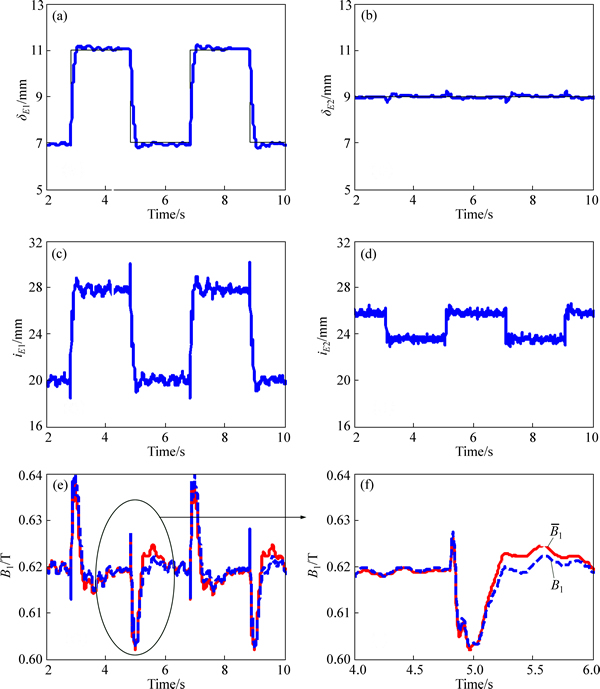
Fig. 8 Performance of module backstepping control system with feedback of virtual magnetic flux signal B1.
References
[1] LI J H, LI J, ZHOU D F, YU P C. Self-excited vibration problems of maglev vehicle-bridge interaction system [J]. Journal of Central South University, 2014, 21: 4184-4192
[2] ZHOU D F, HANSEN C H, LI J. Suppression of maglev vehicle-girder self-excited vibration using a virtual tuned mass damper [J]. J Sound Vib, 2011, 330(5): 883-901.
[3] WAI R J, LEE J D, CHUANG K L. Real-time PID control strategy for maglev transportation system via particle swarm optimization [J]. IEEE Trans Ind Electron, 2011, 58(2): 629-646.
[4] CHEN M Y, LIN T B, HUNG S K, LI C. Design and experiment of a Macro-micro planar maglev positioning system [J]. IEEE Trans Ind Electron, 2012, 59(11): 4128-4139.
[5] ZHANG Y J, CHAI T Y, WANG H. A nonlinear control method based on ANFIS and multiple models for a class of SISO nonlinear systems and its application [J]. IEEE Trans Ind Electron, 2011, 22(11): 1783-1795.
[6] UDDIN M N. An adaptive-filter-based torque-ripple minimization of a fuzzy-logic controller for speed control of IPM motor drives [J]. IEEE Trans Ind Electron, 2011, 47(1): 350-358.
[7] LI J H, LI J, ZHANG G. A practical robust nonlinear controller for maglev levitation system [J]. Journal of Central South University, 2013, 20: 2991-3001.
[8] LI J H, LI J, YU P C, WANG L C. Adaptive backstepping control for levitation system with load uncertainties and external disturbances [J]. Journal of Central South University, 2014, 21: 4478- 4488.
[9] ZHANG W Q, LI J, ZHANG K, CUI P. Stability and bifurcation in magnetic flux feedback maglev control system [J]. Mathematical Problems in Engineering, 2011, 47(1): 350-358.
[10] YI J H, PARK K H, KIM S H, KWAK Y K, ABDELFATAH M, BUSCH I. Robust force control for a magnetically levitated manipulator using flux density measurement [J]. Control Eng Practice, 1996, 4(7): 957-965.
[11] ALBERT T E, OLESZCZUK G, HANASOGE A M. Stable levitation control of magnetically suspended vehicles with structural flexibility [C]// Proceedings of the 2008 American Control Conference. Washington: ACC, 2008: 4035-4040.
[12] TANG Z J, TSUBAKIHARA H, KANAE S, WADA K, SU C Y. A novel robust nonlinear motion controller with disturbance observer [J]. IEEE Trans Contr Syst, 2008, 16(1): 137-147.
[13] BANG J S, SHIM H, PARK S K, SEO J H. Robust tracking and vibration suppression for a two inertia system by combining backstepping approach with disturbance observer [J]. IEEE Trans Ind Electron, 2010, 57(9): 3197-3206.
[14] YAGIZ N, HACIOGLU Y. Backstepping control of a vehicle with active suspensions [J]. Control Engineering Practice, 2008, 16(9): 1457-1467.
[15] TONG S C, HE X L, ZHANG H G. A combined backstepping and small-gain approach to robust adaptive fuzzy output feedback control [J]. IEEE Trans Fuzzy Syst, 2009, 17(5): 1059-1069.
[16] TONG S C, HUO B Y, LI Y M. Adaptive fuzzy output feedback tracking backstepping control of strict-feedback nonlinear systems with unknown dead zones [J]. IEEE Trans Fuzzy Syst, 2012, 20(1): 168-180.
[17] TONG S C, LI Y M. Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures [J]. IEEE Trans Fuzzy Syst, 2014, 22(1): 1-15.
[18] HUA C C, LIU P X, GUAN X P. Backstepping control for nonlinear systems with time delays and applications to chemical reactor systems [J]. IEEE Trans Ind Electron, 2009, 56(9): 3723-3732.
[19] PAN Y P, WANG J. Model predictive control of unknown nonlinear dynamical systems based on recurrent neural networks [J]. IEEE Trans Ind Electron, 2012, 59(8): 3089-3101.
[20] WEN C Y, ZHOU J, LIU Z T, SU H Y. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance [J]. IEEE Trans Ind Electron, 2011, 56(7): 1672-1678.
[21] LIN F J, TENG L T, SHIEH P H. Adaptive backstepping control system for magnetic levitation apparatus using recurrent neural network [J]. IEEE Trans Magn, 2007, 43(5): 2009-2018.
(Edited by YANG Hua)
Foundation item: Projects(11302252, 11202230) supported by the National Natural Science Foundation of China
Received date: 2015-01-22; Accepted date: 2016-01-18
Corresponding author: LI Jie, Professor; Tel: +86-731-84573387-8103; E-mail: jieli@nudt.edu.cn

