
DOI: 10.11817/j.issn.1672-7207.2021.03.031
密缀板耗能格构柱加固既有框架结构的简化分析及工程应用
孟凡涛1, 2,阮兴群2,赵建锋1,张玉明2,柳晓博2,李显杰2
(1. 青岛理工大学 土木工程学院,山东 青岛,266033;
2. 山东华科规划建筑设计有限公司,山东 聊城,252000)
摘要:为了解决既有建筑抗震加固施工过程中使用功能被中断的问题,基于摇摆结构的相关原理,提出一种密缀板耗能格构柱,其密集缀板采用低屈服点钢材的窄翼缘小截面钢梁,而2个柱肢是高屈服点钢材内部灌注高标号补偿收缩混凝土的钢管柱。首先,基于既有钢筋混凝土框架附加弯剪型子结构的方法,建立考虑附加子结构柱底弹性水平约束和弹性转动约束的微分方程,并利用参数取值的变化进行理论研究;然后,为了验证密缀板耗能格构柱对既有钢筋混凝土框架抗震的有利作用,将其应用于既有钢筋混凝土框架分别进行多遇地震和罕遇地震作用下的分析。研究结果表明:多遇地震作用下密缀板耗能格构柱可提供适当的刚度,使得既有钢筋混凝土框架结构的刚度有所提高;罕遇地震作用下,密缀板耗能格构柱能够改善既有钢筋混凝土框架的变形形态和受力状态,使其损伤分布更加均匀,残余变形显著降低。密缀板耗能格构柱在地震作用下屈服耗能,发挥了消能减震作用。
关键词:摇摆结构;分布参数模型;密缀板耗能格构柱;抗震性能;抗震加固
中图分类号:TU352.1+1 文献标志码:A 开放科学(资源服务)标识码(OSID):
文章编号:1672-7207(2021)03-1004-13
Simplified analysis and engineering application of existing frame structure strengthened by energy dissipation lattice column with dense battens
MENG Fantao1, 2, RUAN Xingqun2, ZHAO Jianfeng1, ZHANG Yuming2, LIU Xiaobo2, LI Xianjie2
(1. College of Civil Engineering, Qingdao University of Technology, Qingdao 266033, China;
2. Shandong Huake Planning Architectural Design Co. Ltd., Liaocheng 252000, China)
Abstract: In order to solve the problem that the function of existing buildings can be interrupted during the construction of seismic strengthening, a new type of energy dissipation lattice column with dense battens was proposed based on the related principle of rocking structure. The dense batten adopted narrow flange small section steel beam with low yield point, and the two column legs were steel tube columns with high yield point steel and high grade shrinkage compensating concrete. Firstly, based on the method of reinforced concrete frame with shear-bending substructure, a new method was presented, which took into account the horizontal and rotational elastic constraints at the base of the column. The variation of the parameter value was studied theoretically. Then, in order to verify the beneficial effect of energy dissipation lattice columns with dense battens on the seismic resistance of existing reinforced concrete frames, the analysis of the frequently occurring earthquake and rarely occurring earthquake was carried out, respectively. The results show that the energy dissipation lattice columns with dense battens can provide appropriate stiffness during frequently occurring earthquake, which can improve the stiffness of existing reinforced concrete frame structures. The energy dissipation lattice columns with dense battens can improve deformation and stress state of the existing RC frame, make the damage distribution more uniform, and reduce the residual deformation significantly. The energy-dissipating lattice column with dense battens is subjected to seismic energy dissipation, which plays the role of energy dissipation and shock absorption.
Key words: rocking structure; distributed parameter model; energy dissipation lattice column with dense battens; seismic performance; seismic strengthening
地震作用下控制建筑结构的损伤程度和损伤范围是避免工程结构发生严重破坏的重要措施[1-3]。HOUSNER[4]在1952年加州地震后发现石油裂解塔由于底部基础锚固螺栓的拉伸变形引起结构发生摇摆运动,而没有遭受到严重损坏;1960年智利地震后,因施工质量问题导致基础弱化的高位水槽也出现了摇摆现象[5]。源于上述震害调研现象,HOUSNER[5]提出了“摇摆结构”概念,并建立了经典的摇摆刚体模型。WADA等[6]提出了“损伤可控结构”理念,随后国内外大量学者开始研究摇摆体系对框架结构的损伤控制。
MACRAE等[7]研究了摇摆柱对支撑框架抗震性能的影响,发现摇摆柱的刚度越大,控制层间变形集中度的效果越明显;QU等[8]采用摇摆墙对东京工业大学G3教学楼进行抗震加固,该工程经历了2011年日本9.0级的东日本大地震后,主体结构几乎完好无损;GRIGORIAN等[9]分析表明,摇摆附属构件在一定条件下能够影响结构的极限承载力,并提出了摇摆墙抗弯框架设计的分析方法;吴守君等[10]结合某医院加固工程,指出摇摆墙框架结构能够提高结构体系的耗能能力且减小结构残余变形;冯玉龙等[11]研究底部设置屈曲约束支撑摇摆墙框架结构的抗震性能;蒋庆等[12]研究摇摆铰支桁架-框架结构的抗震性能,发现铰支桁架-框架具有比摇摆墙框架更大的侧向刚度和相近的侧向变形;贾明明等[13]研究了摇摆桁架-钢框架结构,发现采用摇摆桁架-钢框架体系能显著改善和优化钢框架结构的抗震能力;杜永锋等[14]提出了轻型自复位消能摇摆刚架结构,发现轻型消能摇摆架能有效控制结构的变形模式,减小结构的残余变形;LI等[15-17]提出了连续耗能柱,该种耗能柱由可更换的钢制阻尼器连接在2根钢柱上组成,可用于钢筋混凝土框架结构中,也可用于钢框架结构中[18-20],该种耗能柱能够明显提高框架结构的抗震性能。
无论在新建结构中,还是在既有建筑结构抗震加固中,附加摇摆结构成为一种具有广阔应用前景的新型结构形式。既有框架结构附加摇摆式消能减震子结构,克服了框架结构在地震作用下出现层屈服机制的弱点。附加摇摆消能子结构,通过释放附加子结构某些部位的约束,降低地震作用下相应部位的内力反应;摇摆增大了相应部位的位移,为安装消能减震构件提供了必要条件[7]。摇摆式消能减震子结构,在地震作用下消能构件能够产生较大变形进而产生屈服,消耗地震输入的能量,地震过后可将发生屈服破坏的构件更换,快速恢复结构的使用功能。目前附加摇摆子结构的形式主要有附加摇摆墙和附加摇摆桁架。摇摆式消能子结构能够显著提高结构的整体承载能力,层间变形比较均匀,塑性铰的分布比较均匀[10]。附加摇摆消能子结构后,既有框架结构的整体变形能力和延性得到提升,大幅度降低既有框架结构的倒塌概率。
既有钢筋混凝土框架结构附加摇摆墙存在现场施工复杂、施工周期长、摇摆墙地震作用下容易开裂、摇摆墙自重大以及容易放大结构的动力响应等问题。装配式钢结构在这方面则具有明显优势,基于此,本文提出了一种采用密缀板耗能格构柱加固既有钢筋混凝土框架结构的措施。密缀板耗能格构柱是由2个矩形钢管柱肢和在2个柱肢之间沿柱肢高度方向间距比较密集布置的成品H型钢组成。柱肢采用高屈服点钢材的大截面钢管制作而成,其内部灌注高标号补偿收缩混凝土,缀板是采用低屈服点钢材小截面的H型钢制作而成。该种格构柱在地震作用下密缀板首先屈服耗能,吸收地震能量。
当前对摇摆结构的研究中,尚未探讨摇摆结构底部约束变形对摇摆结构受力影响。因此,本文根据结构力学弹性支座的原理,在弯剪型子结构的底部附加弹性约束的形式,推导子结构的位移及内力的表达式,并给出子结构的位移和内力的变化规律;随后,对一个既有钢筋混凝土框架结构通过设置密缀板耗能格构柱进行抗震加固研究,分析密缀板耗能格构柱在既有钢筋混凝土框架抗震加固中所发挥的作用。
1 既有框架-弯剪型附加子结构的分布参数模型
1.1 分布参数模型
既有钢筋混凝土框架结构附加摇摆弯剪型子结构中,弯剪型子结构在每个楼层位置通过设置抗剪连接件与既有钢筋混凝土框架结构相连接。其计算简图如图1所示。既有钢筋混凝土框架结构附加摇摆弯剪型子结构的分布参数模型采用如下假定:
1) 既有钢筋混凝土框架结构采用剪切梁代替,剪切刚度为常数,相当于仅考虑既有钢筋混凝土框架结构的剪切变形[21-22],忽略弯曲变形;
2) 广义弯剪型附加子结构采用既考虑剪切变形又考虑弯曲变形的梁代替,且抗弯刚度和抗剪刚度沿竖向楼层高度均为常数;
3) 2根梁之间紧密接触,轴向力在交界面连续分布。
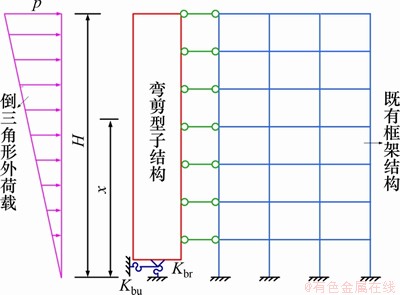
图1 附加摇摆子结构的计算简图
Fig. 1 Calculation diagram of additional rocking substructure
根据材料力学中剪切梁变形的原理,可以得到式(1)。
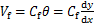 (1)
(1)
式中:Vf为既有钢筋混凝土框架结构的剪力;Cf为既有钢筋混凝土框架结构的抗侧刚度;θ为既有钢筋混凝土框架结构的剪切转角;y为既有钢筋混凝土框架结构与附加摇摆结构的整体侧移;x为既有钢筋混凝土框架结构与附加摇摆结构的计算截面距底部零点的距离。
将式(1)微分得式(2)。
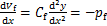 (2)
(2)
式中:pf为附加摇摆结构传递给既有钢筋混凝土框架的反力。附加摇摆结构按弯剪型构件考虑,根据材料力学原理可知,悬臂梁弯曲变形和剪切变形产生的曲率相反,弯曲曲率为
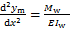 (3)
(3)
式中:ym为附加摇摆构件的弯曲挠度;Mw为附加摇摆构件所承受的弯矩;E为附加摇摆构件的弹性模量;Iw为附加摇摆结构的截面惯性矩。附加摇摆构件的剪切转角如式(4)所示,根据式(4)可以得到剪切曲率,如式(5)所示。
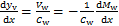 (4)
(4)
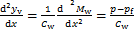 (5)
(5)
式中:Vw为附加摇摆构件所承受的剪力;Cw为附加摇摆构件的抗剪刚度;p为既有钢筋混凝土框架与附加摇摆结构所承受的水平外荷载。考虑附加摇摆结构的剪切变形影响后,则整体结构的侧移为y=ym+yv,对其进行2次微分得到式(6)。
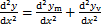 (6)
(6)
将式(3)和(5)代入式(6)可得
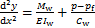 (7)
(7)
对式(7)进行2次微分得式(8)。
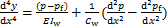 (8)
(8)
本文所考虑的水平外荷载p为倒三角线性分布荷载,将式(2)进行2次微分,代入式(8)可得
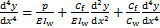 (9)
(9)
化简式(9)可得式(10)。
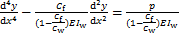 (10)
(10)
令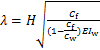 ,
,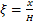 ,得到四阶常系数微分方程:
,得到四阶常系数微分方程:
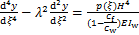 (11)
(11)
式(11)中λ是量纲一的量,为既有钢筋混凝土框架-附加摇摆结构刚度特征值。λ反映既有钢筋混凝土框架和总附加摇摆结构之间刚度比,是影响框架和摇摆结构受力和变形的主要参数。式(11)的通解为:
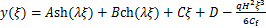 (12)
(12)
1.2 倒三角形荷载下分布参数模型的求解
倒三角形荷载作用下,确定式(12)中任意4个常数的边界条件及平衡方程[23]如下:
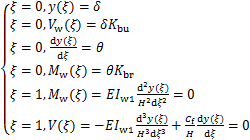 (13)
(13)
式中: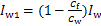 ,利用式(13)中的条件可以得到位移表达式。
,利用式(13)中的条件可以得到位移表达式。
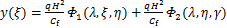 (14)
(14)
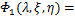
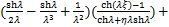
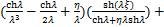
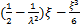 (15)
(15)
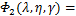
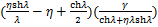 (16)
(16)
式(14)中附加摇摆消能子结构的底部约束转动刚度系数η和底部约束水平刚度系数γ分别由下式确定:
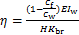 (17)
(17)
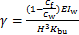 (18)
(18)
η表征附加摇摆结构考虑剪切变形折减的抗弯线刚度与其底部约束转动刚度的比值;γ表征附加摇摆结构考虑剪切变形折减的抗弯线刚度与其底部约束水平刚度的比值。
由式(16)可得:Φ2(λ,η,γ)不是ξ的函数,即Φ2(λ,η,γ)沿结构竖向不变,可理解为附加消能摇摆子结构的底部水平约束刚度产生的结构刚体水平位移。当附加消能摇摆子结构底部铰接时,即Kbu→∞,Kbr→0,则γ→0,η→∞,Φ2(λ,η,γ)→0,结构刚体水平位移消失,式(14)退化为式(19)。
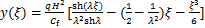 (19)
(19)
当附加消能摇摆子结构底部刚接时,即Kbu→∞,Kbr→∞,则γ→0,η→0,Φ2(λ,η,γ)→0,结构刚体水平位移消失,式(14)退化为式(20)。
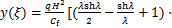
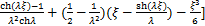 (20)
(20)
根据以上推导的侧移曲线函数,可以得到附加摇摆子结构的弯矩和剪力以及既有钢筋混凝土框架结构的剪力分别如下:
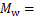
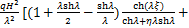
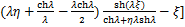 (21)
(21)
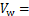
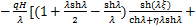
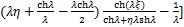 (22)
(22)
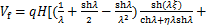
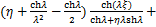
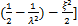 (23)
(23)
1.3 分布参数模型的参数分析
图2所示为λ和η取不同值时结构的位移和内力反应。由图2(a)可知:当λ较小时,结构的侧移接近于直线,且附加摇摆子结构不能改变结构的顶部侧移。由图2(b)可见:随着λ和η增大,附加摇摆子结构的弯矩占比逐渐减小,在λ=3.0和η=3.0时弯矩接近于0,再增大λ和η,弯矩出现负值。根据图2(c)可见:在λ=2.0和η=2.0时,附加摇摆子结构的剪力接近于0,再增大λ和ξ,剪力出现负值。由图2(d)得出:在λ和η均小于1时,随着相对高度ξ增大,剪力呈现逐渐增大的趋势,λ和η均在[1,3]时,剪力随着相对高度ξ增大,出现先增大再减小现象;λ和η均等于4时,剪力随着相对高度ξ增大,出现先增大后减小再增大的现象。
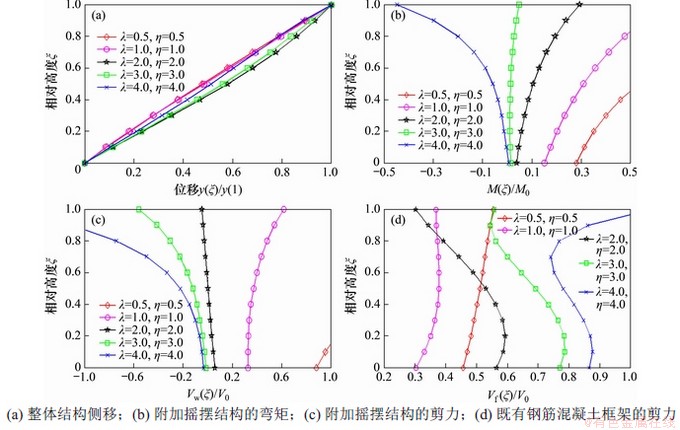
图2 λ和η取不同值时结构的位移和内力反应
Fig. 2 Displacement and internal force responses of structures with different values of λ and η
图3所示为λ固定η取不同值时结构的位移和内力反应。当λ=1.0时,随着η增大,图3(a)中结构的侧移接近于直线,图3(b)中,附加摇摆子结构的弯矩占比逐渐减小。当η取定值时,随着相对高度ξ增大,附加摇摆子结构的弯矩逐渐增大。由图3(c)可见:当λ=1.0时,随着η增大附加摇摆子结构的剪力占比逐渐减小,当η取定值时,随着相对高度ξ增大,附加摇摆子结构的剪力逐渐减小。由图3(d)可见:当λ=1.0时,随着η增大既有钢筋混凝土框架结构的剪力占比逐渐增大;当η取定值时,随着相对高度ξ增大,既有钢筋混凝土框架结构的剪力出现先增大后减小的现象。
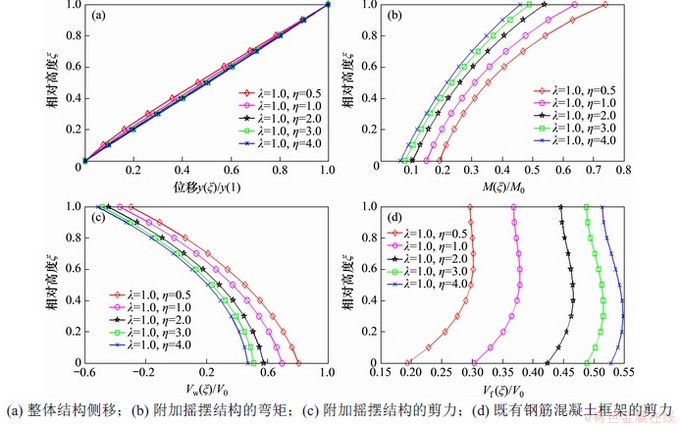
图3 λ固定η取不同值时结构的位移和内力反应
Fig. 3 Displacement and internal force responses of structures with different values of λ and fixed η
2 工程应用
2.1 工程应用背景
山东省某医院门诊病房楼建于20世纪90年代,建筑面积为5 600 m2。工程所在地为Ⅲ类场地,地震分组为第2组,场地特征周期为0.55 s,设计基本地震加速度为0.15g(g为重力加速度)。混凝土强度等级为C30,框架梁、框架柱纵筋及箍筋均为HRB335级钢筋。本工程地上共5层,无地下室,标准层在x向和y向的长度分别为50.4 m和15.3 m,本工程一层平面布置如图4所示。
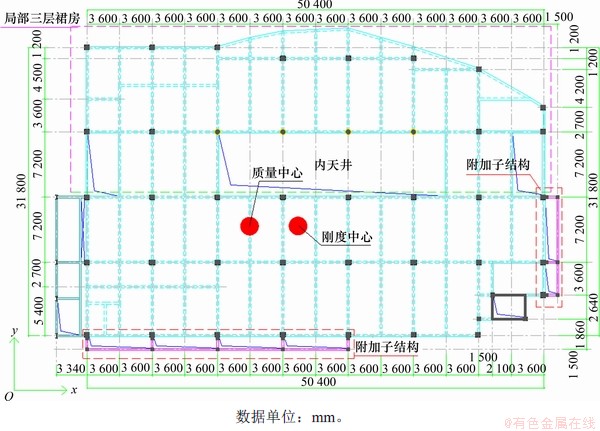
图4 一层结构平面
Fig. 4 First floor structural plan
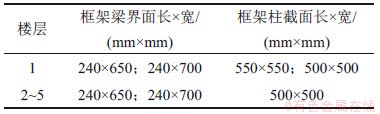
本工程为钢筋混凝土框架结构,经现场复核并核对原设计文件,框架梁、框架柱的截面尺寸如表1所示。经计算,结构的质量中心和刚度中心不重合,扭转效应明显,且底层2个方向的层间位移角均不满足文献[24]要求。
为了改善结构的抗震性能,须进行抗震加固。本工程的门诊病房楼是该医院的主要营业门诊,加固改造中不能停止营业,即内部不能采取大量施工作业,且必须做到对正常营业的最小干扰。鉴于所面临的现实情况,结合本工程所在的场地条件,经慎重考虑,采用室外附加密缀板耗能格构柱的措施,既尽量减少现场作业量,又能最大程度提升本工程的抗震性能,经多次试算,x向设置3榀,y向设置5榀密缀板耗能格构柱,其平面位置如图4所示,单榀密缀板耗能格构柱的立面如图5所示。
表1 既有钢筋混凝土框架结构的构件截面尺寸
Table 1 Section size of existing reinforced concrete frame
2.2 加固方案
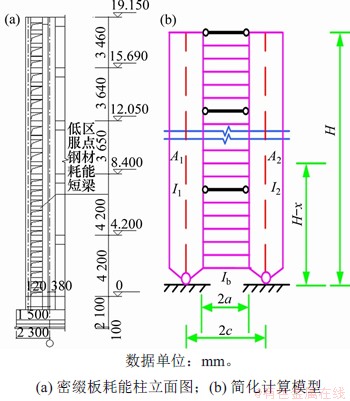
图5 密缀板耗能柱立面及简化计算模型
Fig. 5 Elevation and simplified calculation model of energy dissipation lattice column with dense battens
采用上节所述的密缀板耗能格构柱,可以充分利用原结构基础地梁的外伸部分,无需再额外增加基础底面积,减少现场基础开挖的工作量,加快施工速度。结合既有钢筋混凝土框架结构的楼层刚度,初选密缀板耗能格构柱的截面并经多遇地震作用下的试算,确定密缀板耗能格构柱在x向和y向的施加榀数。根据第1节的公式推导和数值分析,λ越小,既有钢筋混凝土框架结构的刚度越小,密缀板耗能格构柱所发挥的作用越大,最终确定的x向的λ为0.21,y向的λ为0.22。考虑密缀板耗能格构柱的柱脚约束,确定η为152.1,限于篇幅,具体计算过程不再展开论述。根据第1节论述,说明柱肢刚度很大,柱脚可完全按铰接设计。采用YJK进行了多遇地震下的对比分析,增设密缀板耗能格构柱后,2个方向的位移角均能满足文献[24]要求,楼层质量中心与刚度中心已基本重合。设置密缀板耗能格构柱的模型周期与既有钢筋混凝土框架结构的模型周期如表2所示,密缀板耗能格构柱的具体构造:除在楼层处采用与两侧柱肢铰接的截面较大的钢梁外,相邻2个楼层高度范围内的柱肢之间密集的水平缀板(小截面窄翼缘的钢梁)均采用低屈服点钢材Q235B制作而成,柱肢采用Q345B方钢管,内灌补偿收缩C50混凝土。密缀板耗能格构柱的截面尺寸如表3所示。密缀板在地震作用下屈服耗能,震后可拆卸更换,有利于实现震后结构功能的快速恢复。本工程采用附加摇摆密缀板格构柱作为加固方案,既有钢筋混凝土框架结构模型及设置密缀板耗能格构柱加固方案模型如图6所示。楼层处密缀板耗能格构柱之间应加强连接,防止密缀板耗能格构柱的柱肢发生平面外的失稳破坏。
表2 模型计算周期
Table 2 Calculation period of model s
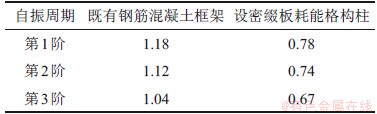
表3 密缀板耗能格构柱截面尺寸
Table 3 Cross-section of energy dissipation lattice column with dense battens
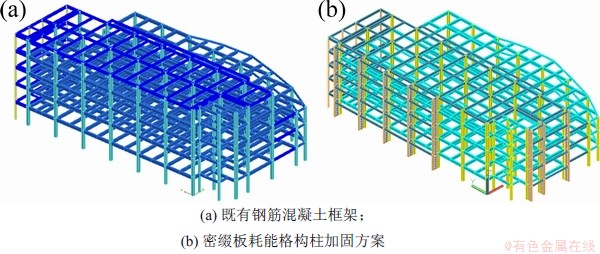
图6 既有钢筋混凝土框架模型和加固方案模型
Fig. 6 Existing reinforced concrete frame model and reinforcement scheme model
基础采用摇摆式柱脚如图7所示,该柱脚在大震下可以转动,释放了格构柱的柱脚约束,有利于密缀板耗能格构柱发挥“摇摆”作用。楼层处密缀板耗能格构柱与既有钢筋混凝土框架在楼层处的连接如图8所示。
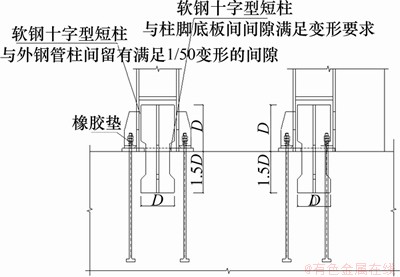
图7 密缀板耗能格构柱的柱脚
Fig. 7 Base of energy dissipation lattice column with dense battens
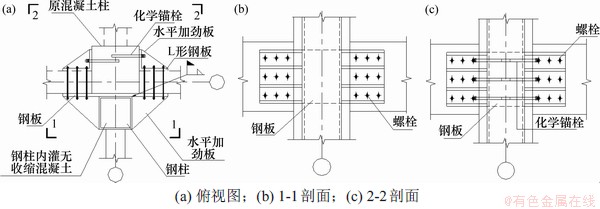
图8 密缀板耗能格构柱与既有钢筋混凝土框架的连接
Fig. 8 Connection of energy dissipation lattice column with dense battens and original frame
3 加固后抗震性能分析
为了检验采用密缀板耗能格构柱加固的既有钢筋混凝土框架结构的抗震性能,本文进行罕遇地震作用下的动力弹塑性时程分析。罕遇地震作用动力弹塑性时程分析所选择的3条波的反应谱如图9所示。设置密缀板耗能格构柱后,既有钢筋混凝土框架结构的屈服路径发生明显变化。在罕遇地震作用下,未采取加固措施时钢筋混凝土框架梁首先出现损伤破坏,而设置密缀板耗能格构柱之后,密缀板首先发生屈服耗能,且在相同地震波作用下,设置密缀板耗能格构柱后,既有钢筋混凝土框架结构的框架柱的损伤有明显降低趋势,这种现象体现了密缀板耗能格构柱的耗能作用。
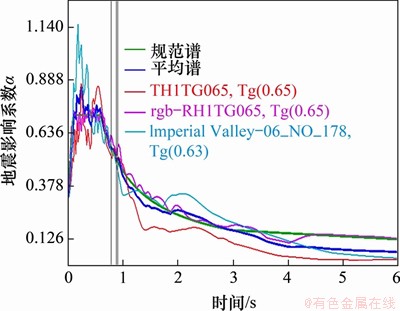
图9 3条地震波谱与规范谱的比较
Fig. 9 Comparison of three seismic spectra with standard spectra
3.1 结构顶点侧移及残余变形对比
罕遇地震作用下,为了检验设置密缀板耗能格构柱加固的效果,对比既有钢筋混凝土框架结构与设置密缀板耗能格构柱后结构顶部相同位置的顶点侧移。图10所示为结构顶点位移时程,由图10可见:既有钢筋混凝土框架结构x向残余变形为33.35 mm,y向残余变形为43.45 mm,通过对比顶点侧移可知,设置密缀板耗能格构柱后,结构的残余变形明显减小,且顶点最大峰值位移也明显减小,主要是因为密缀板通过有效的塑性变形消耗地震输入的能量。
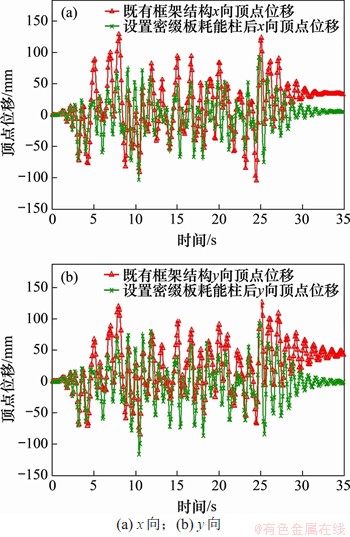
图10 结构顶点位移时程
Fig. 10 Displacement time history of point on building top
3.2 层间位移角
罕遇地震作用下的层间位移角,按照文献[24]规定,框架结构弹塑性层间位移角限值为1/50(0.02) rad。图11所示为5个楼层的层间位移角,由图11可见:设置密缀板耗能格构柱后,结构的层间位移角明显减小,根据文献[24]附录M所给的罕遇地震作用下层间位移角的参考指标示例,罕遇地震下加固后,x向和y向最大弹塑性层间位移角分别为1/123和1/135,均出现在第2层。
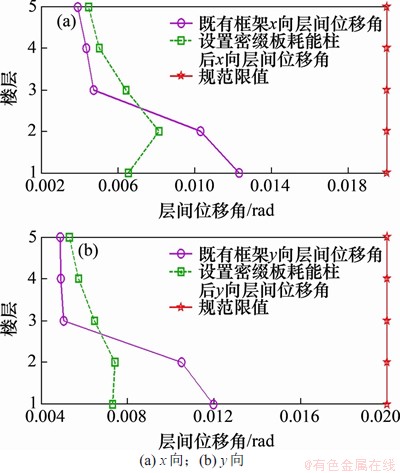
图11 5个楼层的层间位移角
Fig. 11 Inter-story drift of five floors
3.3 层间位移不均匀系数
根据文献[7],采用层间位移不均匀系数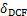 作为衡量结构侧向变形模式和层间损伤集中效应的参数指标,其定义为结构最大层间位移角与顶点位移的比,如式(24)所示。
作为衡量结构侧向变形模式和层间损伤集中效应的参数指标,其定义为结构最大层间位移角与顶点位移的比,如式(24)所示。
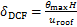 (24)
(24)
式中:θmax为所有楼层的最大层间位移角;uroof为结构顶点位移;H为结构总高度。当结构各层层间位移相同时,δDCF=1,δDCF越接近1,说明结构的层间位移角和损伤比较均匀。δDCF由结构所受水平荷载的分布模式、结构沿竖向的刚度分布和结构的损伤机制决定。采用密缀板耗能格构柱加固后,x向δDCF为1.31,y向δDCF为1.23,而未经加固时框架结构x向δDCF为1.835,y向δDCF为1.830。因此,结构的层间变形集中度得到了明显改善。
3.4 整体结构的抗震性能评估
根据罕遇地震作用下,动力弹塑性时程分析结果,x向和y向的耗能分别如图12所示,2个方向的非线性耗能均约为40%,说明2个方向的结构布置比较合理。2个方向统计得到的每条波作用下的非线性耗能如图13所示。为进一步比较密缀板耗能格构柱的耗能特性,x向和y向不同地震波下的抗侧力构件的耗能比统计如图14所示,由图14可见:所采用的密缀板耗能格构柱在每条波作用下均发挥了耗能作用,x向最小为32.21%,y向最小为28.25%。
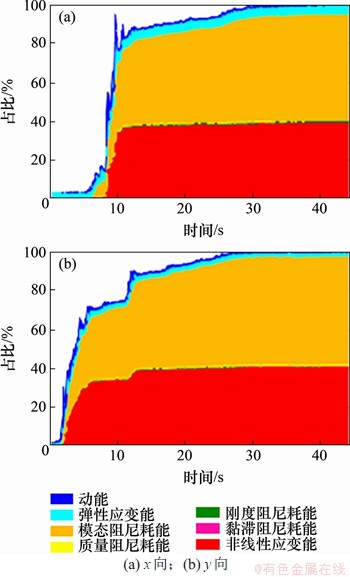
图12 结构的能量统计
Fig. 12 Energy statistics of structure
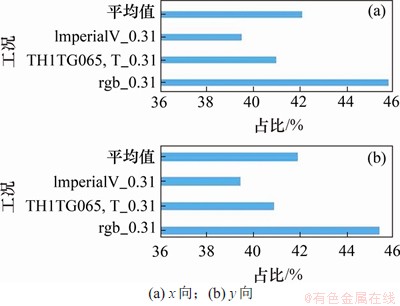
图13 结构非线性耗能占总耗能比值
Fig. 13 Ratio of nonlinear energy to total energy
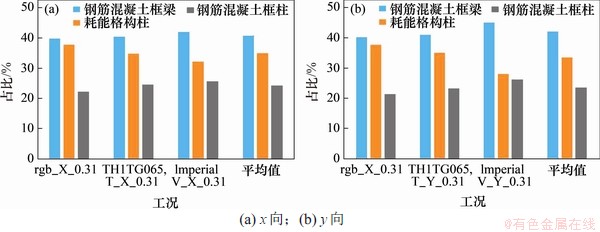
图14 主要构件非线性耗能占总非线性耗能的比值
Fig. 14 Ratio of nonlinear energy consumption of main components to total nonlinear energy consumption
按照文献[24]附录M的要求和文献[25]的相关规定,进行构件的性能复核,结果如图15所示。由图15(a)可见:既有钢筋混凝土框架柱约72%处于轻微破坏状态,个别框架柱出现轻度破坏。由图15(b)可见:约65%的钢筋混凝土框架梁处于轻微损伤状态。由图15(c)可见:统计得到的密缀板耗能格构柱的柱肢个别位置出现中度损坏或轻微损坏,大部分处于无损坏状态。由图15(d)可见:约5%的缀板出现中度损坏,30%的缀板出现轻度损坏,18%的缀板出现了轻微损坏。这充分证明,所预设的密缀板耗能格构柱能够在罕遇地震作用下消耗一部分能量,发挥消能减震的作用。
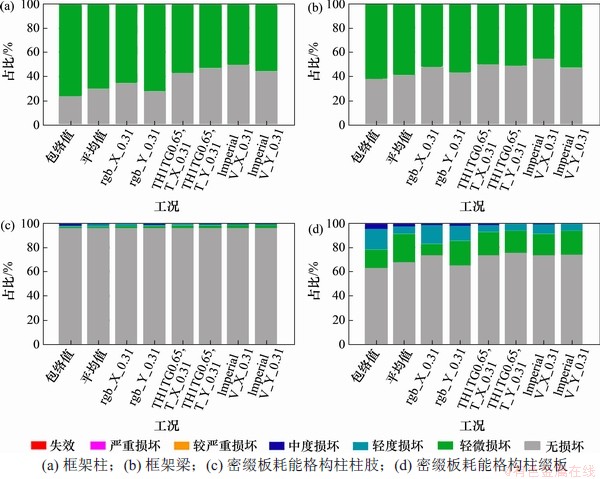
图15 抗侧力构件正截面损伤统计
Fig. 15 Statistics of normal section damage of lateral force resisting members
4 结论
1) 考虑附加子结构柱脚刚度的影响,对既有钢筋混凝土框架结构采用附加弯剪型子结构的方式进行加固,给出分布参数模型在倒三角形荷载下的计算公式。
2) 附加子结构柱脚水平方向的位移仅能引起结构的刚体位移,附加子结构的柱脚转动刚度影响结构的整体侧移和附加子结构与既有钢筋混凝土框架之间的内力分布。
3) 附加子结构的剪切变形影响相对刚度,进而影响附加子结构与既有钢筋混凝土框架之间的外荷载分担比。
4) 密缀板耗能格构柱在多遇地震作用下对既有钢筋混凝土框架结构提供适当的刚度。罕遇地震作用下,密缀板耗能格构柱屈服耗能,发挥消能减震作用,改善既有钢筋混凝土框架结构的变形形态和受力状态,使得既有钢筋混凝土框架的损伤分布更加均匀,残余变形显著降低。
参考文献:
[1] VERDE R V. Explanation for the numerous upper floor collapses during the 1985 Mexico City earthquake[J]. Earthquake Engineering & Structural Dynamics, 1991, 20(3): 223-241.
[2] EQE. The January 17, 1995 Kobe Earthquake-An EQE Summary Report, EQE International, 1995[R].
[3] ZHAO Bin, TAUCER F, ROSSETTO T. Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China[J]. Engineering Structures, 2009, 31(8): 1707-1723.
[4] HOUSNER G W. The Behavior of inverted pendulum structures during earthquakes [J]. Bulletin of the Seismological Society of America, 1963, 53(2): 403-417.
[5] HOUSNER G W. Limit design of structures to resist earthquakes[C]// Proceedings of the 1st World Conference on Earthquake Engineering. Berkeley, California, 1956: 1-12.
[6] WADA A, CONNOR J J, KAWAI H, et al. Damage tolerant structures [C]// Proceedings of Fifth US-Japan Workshop on the Improvement of Building Structural Design and Construction Practices. San Diego, California, USA: Applied Technology Council, 1992: 27-39.
[7] MACRAE G A, KIMURA Y, ROEDER C. Effect of column stiffness on braced frame seismic behavior[J]. Journal of Structural Engineering, 2004, 130(3): 381-391.
[8] QU Zhe, WADA A, MOTOYUI S, et al. Pin-supported walls for enhancing the seismic performance of building structures[J]. Earthquake Engineering & Structural Dynamics, 2012, 41(14): 2075-2091.
[9] GRIGORIAN C E, GRIGORIAN M. Performance control and efficient design of rocking-wall moment frames[J]. Journal of Structural Engineering, 2016, 142(2): 04015139.
[10] 吴守君, 潘鹏, 张鑫. 框架-摇摆墙结构受力特点分析及其在抗震加固中的应用[J]. 工程力学, 2016, 33(6): 54-60.
WU Shoujun, PAN Peng, ZHANG Xin. Characteristics of frame rocking wall structure and its application in aseismic retrofit[J]. Engineering Mechanics, 2016, 33(6): 54-60.
[11] 冯玉龙, 吴京, 孟少平. 连续摇摆墙-屈曲约束支撑框架抗震性能分析[J]. 工程力学, 2016, 33(S1): 90-94.
FENG Yulong, WU Jing, MENG Shaoping. Seismic performance analysis of continuously rocking wall-buckling restrained braced frames[J]. Engineering Mechanics, 2016, 33(S1): 90-94.
[12] 蒋庆, 王瀚钦, 冯玉龙, 等. 铰支桁架-框架结构抗震设计与性能研究[J]. 工程力学, 2019, 36(3): 105-113.
JIANG Qing, WANG Hanqin, FENG Yulong, et al. Seismic design and performance of hinged truss frame structures[J]. Engineering Mechanics, 2019, 36(3): 105-113.
[13] 贾明明, 周洲, 吕大刚, 等. 摇摆桁架-钢框架结构的刚度比需求及地震响应分析[J]. 工程力学, 2018, 35(10): 66-74.
JIA Mingming, ZHOU Zhou, LU Dagang, et al. Demand stiffness ratio and earthquake response analysis of rocking truss-steel frame system[J]. Engineering Mechanics, 2018, 35(10): 66-74.
[14] 杜永峰, 武大洋. 基于刚度需求设计的轻型消能摇摆架减震性态分析[J]. 土木工程学报, 2014, 47(1): 24-35.
DU Yongfeng, WU Dayang. Performance analysis of light energy dissipative rocking frame designed on the basis of stiffness demand[J]. China Civil Engineering Journal, 2014, 47(1): 24-35.
[15] LI Yanwen, LI Guoqiang, JIANG Jian, et al. Mitigating seismic response of RC moment resisting frames using steel energy-dissipative columns[J]. Engineering Structures, 2018, 174: 586-600.
[16] LI Yanwen, LI Guoqiang, JIANG Jian, et al. Experimental study on seismic performance of RC frames with Energy-Dissipative Rocking Column system[J]. Engineering Structures, 2019, 194: 406-419.
[17] LI Yanwen, LI Guoqiang, JIANG Jian, et al. Modeling of behavior of continuous energy-dissipative steel columns under cyclic loads[J]. Journal of Earthquake Engineering, 2019, 23(9): 1560-1583.
[18] LI Yanwen, LI Guoqiang, SUN Feifei. 11.16: Seismic performance evaluation of MRFS with dissipative continuous columns[J]. Proceeding of Eurosteel, 2017, 1(2/3): 2966-2974.
[19] LI Yanwen, LI Guoqiang, SUN Feifei, et al. Experimental study on continuous energy-dissipative steel columns under cyclic loading[J]. Journal of Constructional Steel Research, 2018, 141: 104-117.
[20] LI Yanwen, LI Guoqiang, JIANG Jian, et al. Use of energy-dissipative rocking columns to enhance seismic performance of buckling-restrained braced frames[J]. Journal of Constructional Steel Research, 2019, 159: 548-559.
[21] 孟焕陵, 沈蒲生. 框-剪结构考虑墙肢剪切变形时剪力墙合理数量[J]. 湖南大学学报(自然科学版), 2005, 32(6): 6-10.
MENG Huanling, SHEN Pusheng. Optimal quantity of shear walls in frame-shear wall structures with influence of shear deformation of shearwalls[J]. Journal of Hunan University(Natural Science), 2005, 32(6): 6-10
[22] 孟凡涛, 张玉明, 阮兴群. 考虑剪切变形的半刚性连接钢框架P-Δ效应研究[J]. 应用力学学报, 2013, 30(1): 136-140.
MENG Fantao, ZHANG Yuming, RUAN Xingqun. P-Δ effects analysis of steel frame with semi-rigid connection and shear deformation[J]. Chinese Journal of Applied Mechanics, 2013, 30(1): 136-140.
[23] 傅学怡, 邸博. 基于有限基础刚度的框架-剪力墙结构抗震设计[J]. 土木工程学报, 2014, 47(4): 29-37.
FU Xueyi, DI Bo. Seismic design of frame-shear wall structures with finite foundation stiffness[J]. China Civil Engineering Journal, 2014, 47(4): 29-37.
[24] GB 50011-2010. 建筑抗震设计规范[S].
GB 50011—2010. Code for seismic design of buildings[S].
[25] DBJ/T 15—151—2019. 建筑工程混凝土结构抗震性能设计规程[S].
DBJ/T15—151—2019. Specification for performance-based seismic design of reinforced concrete building structure[S].
(编辑 秦明阳)
收稿日期: 2020 -03 -20; 修回日期: 2020 -05 -21
基金项目(Foundation item):国家自然科学基金资助项目(51778314);山东省住房和城乡建设厅研究开发项目(2020-K3-9,2021-K2-2) (Project (51778314) supported by the Natural Science Foundation of China; Projects(2020-K3-9, 2021-K2-2) supported by Research and Development Program of Housing and Urban-Rural Development Department of Shandong Province)
通信作者:赵建锋,副教授,从事结构抗震研究;E-mail:zhaojf@qut.edu.cn
引用格式: 孟凡涛, 阮兴群, 赵建锋, 等. 密缀板耗能格构柱加固既有框架结构的简化分析及工程应用[J]. 中南大学学报(自然科学版), 2021, 52(3): 1004-1016.
Citation: MENG Fantao, RUAN Xingqun, ZHAO Jianfeng, et al. Simplified analysis and engineering application of existing frame structure strengthened by energy dissipation lattice column with dense battens[J]. Journal of Central South University(Science and Technology), 2021, 52(3): 1004-1016.