Trans. Nonferrous Met. Soc. China 31(2021) 345-357

New constitutive equation utilizing grain size for modeling of hot deformation behavior of AA1070 aluminum

H. R. REZAEI ASHTIANI, A. A. SHAYANPOOR

School of Mechanical Engineering, Arak University of Technology, Arak, 38135-1177, Iran

Received 21 March 2020; accepted 1 December 2020

Abstract: A new phenomenological and empirically-based constitutive model was proposed to modify the term in the original Johnson-Cook constitutive model. The new model can be used to describe and predict the flow stress of AA1070 aluminum with different initial grain sizes in the hot working process. This developed model considers thermal softening, strain-rate hardening, strain hardening, initial grain size, and interactions with each other and can correctly model the behavior of AA1070 at elevated temperature with different strains, strain rates, and initial grain sizes. The hot flow behavior of AA1070 was investigated through compression tests over wide ranges of temperature from 623 to 773 K, strain rate from 0.005 to 0.5 s^-1 and initial grain size from 50 to 450 μm. Results show that the initial grain size has a significant effect on the flow behavior of AA1070. Then, correlation coefficient (R), average absolute relative error (AARE), and relative error were examined for comparative predictability of the model. Results show that flow stresses for different initial grain sizes calculated by the new proposed model perfectly correlate with experimental ones, with a mean relative error of 1.19%, which confirms that the new modified Johnson-Cook relation can give a precise estimation of the hot flow stress of AA1070 aluminum by considering the initial grain size.

Key words: constitutive equation; modified Johnson-Cook model; initial grain size; flow stress; hot deformation; AA1070 aluminum

1 Introduction

Pure aluminum has become increasingly important in different industries such as the transportation infrastructures, packaging of food and beverages, buildings construction, electricity transmission, and production of the durable consumer because of its lightweight, high specific strength, good fracture toughness, and corrosion resistance [1,2].

As one of the necessary processes in the manufacturing engineering, deformation at elevated temperature is an essential step to control the structure at the micro-level and also performance. Process parameters like deformation temperature, strain, and strain rate do influence softening/ hardening evolutions. The behavior of material flow is a manifestation of work hardening, work- softening, dislocation annihilation, polygonization, and dynamic recrystallization (DRX) and it can evaluate the performance of hot deformation process [3]. It is unanimously accepted that the mechanics of the majority of metals is dependent on both temperature and strain rate. When metals and/or alloys undergo hot deformation, they are subjected to a complex combination of strain rate, strain, and temperature histories. So, the hot flow trend of the pure aluminum is considerably complicated at various deformation states and would be reflected by establishing a suitable constitutive model. Moreover, some of the already developed constitutive equations were based on experimental data to correlate the plastic flow stress with temperatures, strain, and strain rate in some conventional hot forming processes [4-8].

To set the optimum process parameters and achieve more favorable mechanical properties, it is worthwhile to know the influence of initial grain size on the flow stress under hot formation. Recently, some studies have focused on initial grain size and how it influences the hot forming of the commercial pure aluminum [9], 7075 aluminum alloy [10], Mg-3Al-1Zn alloy [11], GCr15 steel [12], 304 stainless steel [13], Mg-2Zn alloy [14], 2219 aluminum alloy [15], magnesium alloys [16], and AZ31B [17]. Such investigations showed with lower grain sizes at a constant strain and strain rate in room temperature environment, the flow stress increases. The effect of the grain size on the deformation at ambient temperature is typically demonstrated by Hall-Petch (H-P) equation [18]:

σ_y=σ₀+kd^-1/2                                              (1)

where σ_y is the yield strength, σ₀ is the friction stress for dislocation movement, k is H-P slope and d is the grain size. In this relation, yield stress increases with the inverse square root of the grain size. The critical grain size can be anticipated by this model when there is a transition from dislocation glide flow to twinning-dominated flow. At higher temperatures, the role of grain size in the flow stress can be complex due to the initiation of discontinuous dynamic recrystallization. The effect of grain size on the mechanical response has been concentrated by some studies. For example, MEYERS et al [19] proposed that the grain size possesses a Hall-Petch impact on critical stress for twinning. It was reported that the twinning capability decreases with lower grain sizes due to higher critical stress for the twinning onset. BARNETT et al [20] considered wrought Mg-3Al-1Zn under warm compression and determined the influence of the deformation conditions on the Hall-Petch parameters.

The reliability of simulated results is generally determined by the accuracy of the expressed constitutive equation. Several types of constitutive models including empirical, semi-empirical, phenomenological, physical-based, and artificial neural networks (ANN) have been constructed to predict the variation in flow stress at different deformation temperatures and strain rates [21-24]. Phenomenological models have been developed based on empirical observation using macroscopic mechanical test results, where material parameters can be specified from fitting the experimental data and there are no physical characteristics that are taken into consideration. The Johnson-Cook (J-C) model [25], Khan-Huang-Liang (K-H-L) model [26], and Arrhenius-type constitutive  model [27] are phenomenological models, which are widely applied to predicting the hot deformation of materials. REZAEI ASHTIANI et al [28] investigated the role of grain size in hot working for commercially pure aluminum. CAI et al [29] developed a suitable modified J-C relation for Ti-6Al-4V alloy with compression experiments at temperatures between 1073 and 1323 K and strain rate from 0.001 to 1 s^-1. CHE et al [30] proposed an integrated JC–ZA model, which considers the effect of grain size, strain hardening, strain rate hardening, thermal softening, and the coupled effects of strain, strain rate, and temperature for Ti-6Al-4V by tensile test at a wide range of strain rate (0.1-7500 s^-1), temperature (25-800 °C) and grain size (5-20 μm). In their model, the first term comes from the modified Khan-Huang-Liang (KHL) model, which incorporates the Hall-Petch relation for considering the effect of grain size on yield stress at room temperature. KHAN et al [31] studied the response of nanocrystalline materials to quasi-static and dynamic loading. They achieved the Khan-Huang-Liang (KHL) model which considers the effect of grain size in nanometer. They modified their model in the years of 2000 [31], 2006 [32] and 2009 [33]. Their evaluation gave an excellent correlation with the experimental observations, as compared to the single linear Hall-Petch relation in the entire range of grain sizes at room temperature. ANN model is an artificial intelligence approach that models the flow behavior of the material in terms of input-output complex paradigm but offers no physical insight on the deformation mechanism [34,35]. REZAEI ASHTIANI and SHAHSAVARI [36] compared the ANN, J-C, Arrhenius-type, and strain compensation Arrhenius-type models, and showed that compared with phenomenological approaches, ANN has the highest capability to reveal the hot deformation phenomenon.

Although great progress in the development of material constitutive models has been made, mathematical models (phenomenological, physical, and ANN) are still not advanced enough to consider for the whole complexity of the dynamic response of metals. However, few analytical studies have been found for the relation between flow stress and grain size in the aluminum-based alloys at elevated temperatures. In this work, the effects of initial grain size, strain rate, and deformation temperature on hot deformation behavior of AA1070 aluminum were investigated by isothermal hot compression tests. A new modified Johnson-Cook relation for AA1070 aluminum was developed and introduced to relate flow stress, initial grain size, strain rate, and temperature. This assumption helps to work out the necessary parameters that can be confirmed by only a few data and thus reduce the times of experiments. This can be very useful for improving the performance of this material.

2 Experimental

The chemical composition of AA1070 aluminum employed in this investigation is listed in Table 1. The pure aluminum samples were prepared in a cylindrical shape with a height and diameter of 15 mm and 10 mm, respectively, for compression test according to ASTM: E-209 standard. Electrolytically anodized samples were examined with a polarized light microscope (PLM) to yield a high resolution of grain size. First, specimens were polished or electropolished. Then, they were electrolytically anodized using both Barker’s reagent and HF (4 mL HBF₄ + 0.5 mL HF and 200 mL H₂O) with 20 V electrical voltage for 70 s. Final samples were observed with PLM. This method is mostly applied to detecting recovery and recrystallization onset. Variant initial grain sizes of AA1070 aluminum specimens (50, 150 and 450 μm) were employed (as shown in Fig. 1) [9].

Table 1 Chemical composition of AA1070 (wt.%)

To determine the true strain-stress values of the alloy, uniaxial one-hit hot compression tests were performed using a Gotech-AI7000 servo-controlled machine with an electrical resistance furnace. True stress values were recorded using a high accuracy load cell (Model: SSMDJM-20 kN). A thin mica sheet was put between punch and specimen to lubricate and reduce friction. All specimens achieved a specified temperature with a constant rate of 5 K/min and then soaked for 4 min to ensure homogenous temperature distribution throughout specimens. Uniaxial compression experiments were performed up to the true strain of 0.5 at different temperatures of 623, 723 and 773 K with different strain rates of 0.005, 0.05 and 0.5 s^-1, and different initial grain sizes of 50, 150 and 450 μm. After tests, quenching deformed samples  in cool water was immediately performed to  sustain their microstructure after deformation and prevent undesirable microstructural alterations (recrystallization or grain growth).

Fig. 1 PLM polycrystalline microstructures of AA1070 aluminum with different grain sizes

3 Result and discussion

3.1 Curves of flow stress

The true stress-strain curves of AA1070 aluminum were measured to reflect the high- temperature flow behavior. Figure 2 shows these curves obtained from hot compression tests of AA1070 with three different initial grain sizes under different deformation conditions [9]. It was reported that the flow stress of the aluminum with different microstructures is readily influenced by deformation temperature and strain rate [37,38]. The sensitivities of deformation temperature, strain rate, and grain size on peak flow stress are illustrated in Fig. 3. When the strain rate is high (0.5 s^-1), there is not sufficient time for the dislocation reaction and nucleation of recrystallization and at this strain rate, stress decreases with increasing grain size and temperature, and when the strain rate is low (lower than 0.5 s^-1), stress decreases with decreasing initial grain size and increasing temperature. When the deformation temperature is high, the thermal diffusion activation energy of the material enhances and as a result, the dislocation motion increases. Local atomic diffusion governs this process and it supports dynamic recovery of the dislocation substructures. Since the diffusion phenomenon is the dominant mechanism at high temperatures including hot working [39], in this study, both deformation temperatures and strain rates are considered that account for temperature and time. Consequently, the peak stress increases with increasing strain rate and decreasing temperature [40,41]. It is noteworthy that the flow stress increases with increasing grain size at high temperatures. This effect is readily different in comparison with flow stress at room temperature. This might be attributed to the change from dislocation glide (DG) dominant to grain boundary sliding (GBS) dominant deformation mechanism when the temperature is high and grain size is reduced. As a result, flow stress decreases effectively with a decrease in initial grain size at elevated temperature. Therefore, the material behaves opposite to the DG regime anticipated by the Hall-Petch equation [42]. Results show that in addition to the deformation temperature, the deformation rate is also an important parameter in determining the deformation mechanism, as the deformation mechanism tends to DG with increasing the deformation rate or stain rate. The experimental results show that the flow stresses decrease with increasing the grain size at the elevated temperature and strain rate of 0.5 s^-1. For small values of strain rates (lower than 0.5 s^-1), the flow stresses decrease with decreasing the initial grain size, which can be related to the GBS as a dominant mechanism under this condition, whereas the deformation mechanism changes to DG for high values of strain rates [42]. The decrease of flow stress with decreasing grain size (at lower strain rate) could be connected to the fact that the microstructures with smaller initial grain sizes have higher grain boundary per unit area than those with coarse initial grain sizes. Thus, due to the high density of the grain boundary in the fine grain structure, conditions are provided for the activation of the GBS deformation mechanism and therefore these factors reduce flow stress of material during deformation.

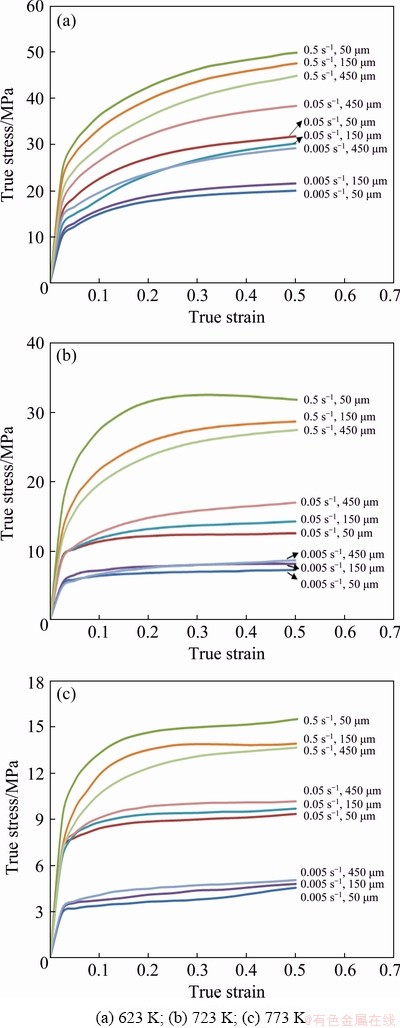
Fig. 2 True strain-stress of AA1070 aluminum at various initial grain sizes, strain rates and temperatures [9]

Fig. 3 Impact of strain rate, process temperature, and primary grain size on maximum flow stress

Analysis of the stress-strain curves under different conditions shows that the flow stress increases at a rapid rate during the initial stage of deformation due to strain hardening phenomenon where dislocation generation, multiplication, and entanglement occur. After this steady increment, the work hardening rate starts to decrease, and flow stress eventually reaches a peak value before it keeps steady or experiences a slight increment until the final forming state. The attainment of steady-state values of flow stress with increasing temperature is a clear indication of thermal softening processes. The steady-state is achieved by dynamic recovery (DRV) [43]. Annihilation and rearrangement of dislocation happen there, which can neutralize strain hardening. Finally, there comes a situation in which dislocation generation speed caused by deformation is completely neutralized by annihilation or rearrangement of dislocation. In other words, the equilibrium between dynamic softening and work hardening occurs.

3.2 Establishment of new constitutive models

3.2.1 Johnson-Cook (J-C) model

The J-C relation was introduced by JOHNSON and COOK [44]. This model is appropriate for describing the stress and strain relations of metallic materials under conditions of large deformation, high strain rate and high temperature. According to the original J-C model, the flow stress is expressed as [41]

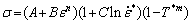            (2)

where (von Mises) stress is shown with σ, the reference yield stress is A, strain hardening coefficient is shown by B and its exponent is illustrated with n. C and m are material constants that represent the coefficient of strain rate hardening and thermal softening exponent, respectively. ε is the plastic strain,  is dimensionless strain rate at a strain rate of  and reference strain rate of , and homologous temperature T^* is can be written as

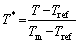                             (3)

where T is the thermodynamic temperature, T_m melting temperature and T_ref reference temperature (T ≥T_ref). The minimum temperature of the tested matrix was selected as reference temperature. The J-C model considers isotropic hardening, strain rate hardening, and thermal softening. But, as three independent phenomena can be isolated from each other [45], the total effect of strain hardening, strain rate hardening, and thermal softening on flow stress can be calculated by multiplying these three terms, i.e. the first, the second, and the third item in Eq. (2). It can be found that the original Johnson-Cook model requires fewer material constants and also few experiments to evaluate these constants.

The original J-C model does not include the initial grain size effect; instead, it assumes that three effective parameters of temperature, strain and strain rate are decoupled. Johnson-Cook model presumes that three parts are thermal softening, strain hardening, and strain rate hardening and they can be thought isolated from each other. The coupled effects of temperatures, strain rates, strain, and grain size on the flow behaviors of the aluminum should be considered. Thus, here, a new modified J-C model is developed to study the hot deformation behavior of AA1070 aluminum. The new modified Johnson-Cook model considers the strain rate and strain hardening part of the original Johnson-Cook model and the coupled effects of the temperature, grain size, and strain rate on the flow behaviors.

3.2.2 New modified Johnson-Cook model

The J-C constitutive model is a type of phenomenological model and is successfully used for a variety of materials in different ranges of temperature and strain rate. The new modified J-C model considering grain size effects can be expressed as

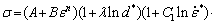
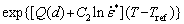         (4)

where A is the flow stress at the reference temperature, strain rate, and initial grain size which is measured to be 15.24 MPa. B, C₁, C₂ and λ are material constants. 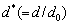 is dimensionless initial grain size, where d and d₀ are initial grain size and reference initial grain size, respectively. Q(d) is a polynomial of the initial grain size. This model assumes four items consisting of strain hardening, initial grain size influence, strain rate hardening, and thermal softening. In this work, the minimum experimental temperature and initial grain size value were used as reference temperature (T_ref) and reference initial grain size (d₀), which in the present case are 623 K and 50 μm, respectively and 0.05 s^-1 is considered as a reference strain rate ().

(1) Specifying material constants n and B

At the deformation temperature of 623 K, the strain rate of 0.05 s^-1, and the initial grain size of 50 μm, Eq. (4) can be rewritten as

σ=(A+Bεⁿ)                              (5)

or

ln(σ-A)=ln B+nln ε                      (6)

By replacing experimental true stress-strain points at the reference state, the curve between ln(σ-A) and ln ε is gained, as depicted in Fig. 4. The value of n and B as 0.4861 and 24.34192 MPa were calculated from the slope and intercept of the fitted line, respectively.

(2) Determination of constant λ

With reference temperature and strain rate of 623 K and 0.05 s^-1, respectively, Eq. (4) can be expressed as

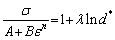                        (7)

The relation between σ/(A+Bεⁿ) and ln d^* at different grain sizes is obtained (Fig. 5). λ value of 0.0529 can be calculated by choosing a series of strains (0.1-0.5) at various grain sizes, from the slope of the fitted line.

Fig. 4 Correlation between ln(σ-A) and ln ε at 623 K with strain rate 0.05 s^-1 and initial grain size of 50 μm

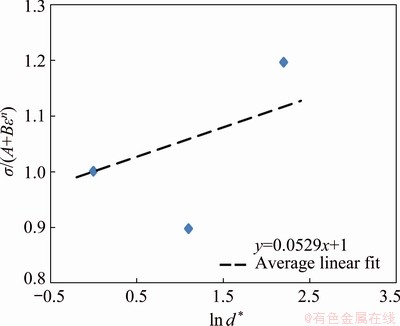
Fig. 5 Correlation between σ/(A+Bεⁿ) and ln d^* at 623 K and strain rate of 0.05 s^-1

(3) Determination of constant C₁

At the reference temperature of 623 K, the flow softening does not occur, and Eq. (4) is presented as

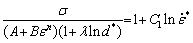             (8)

The relation between σ/[(A+Bεⁿ)(1+λln d^*)] and 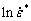 is obtained, as shown in Fig. 6, at various strain rates. The C₁ value can be evaluated by selecting a series of strain (0.1-0.5) and in the different initial grain sizes at various strain rates using the slope of the fitted line, which is obtained to be 0.1517.

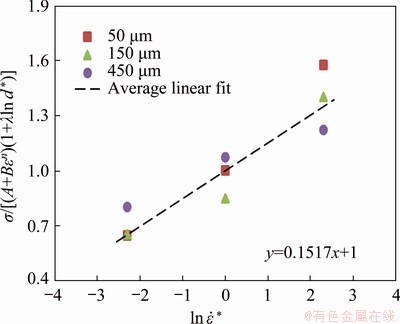
Fig. 6 Relationship between σ/[(A+Bεⁿ)(1+λln d^*)] and 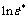at temperature of 623 K

(4) Determination of constant Q(d)

At the reference strain rate of 0.05 s^-1, Eq. (4) is rewritten as

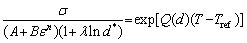     (9)

or

        (10)

The relation between ln{σ/[(A+Bεⁿ)(1+λln d^*)]} and (T-T_ref) at different initial grain sizes and strains can be specified according to Fig. 7. For three variant grain sizes, three slopes are calculated, and then Q(d) is found using the polynomial fit, as illustrated in Fig. 8.

(5) Determination of constant C₂

At the final stage to establish the modified J-C model, a new parameter S is introduced. Then, Eq. (4) can be presented as

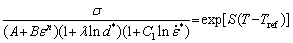   (11)

or

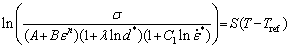  (12)

where 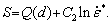 Parameter S is related to the initial grain size and strain rate. The relationship between  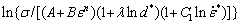  and (T-T_ref) can be used to obtain the value of S. Now, the C₂ value is calculated by the correlation between (S-Q(d)) and 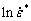, as shown in Fig. 9. Three sets of C₂ are obtained at three grain sizes. To determine the optimum set of C₂ value, an average absolute relative error (AARE) is used. Such an error’s standard unbiased statistical parameter can be presented in Eq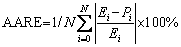. (13):

             (13)

where E_i are the experimental data points and P_i are predicted data taken from the developed constitutive equations. The overall number of data points employed in this study is presented with N. With minimizing the AARE value between experimental and predicted flow stress, the optimization of the model can be performed by the minimization of the difference between experimental and predicted value. The values of AARE for the initial grain sizes of 50, 150, and 450 μm are gained to be 1.41, 1.19, and 1.24, respectively. The minimum AARE value coincides with the initial grain size of 150 μm and the corresponding value of C₂ is 0.0007. Consequently, after determining material constants, the constitutive equation of AA1070 aluminum based on the new modified J-C model can be summarized as

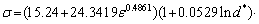
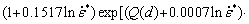
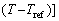
Q(d)=8×10^-5ln²d^*-2×10^-5ln d^*-0.0079       (14)

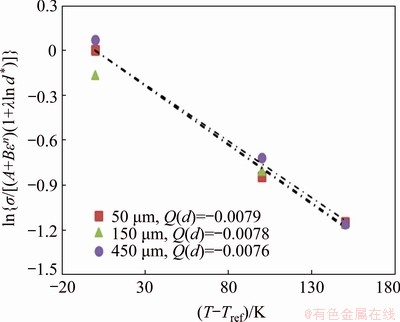
Fig. 7 Relationship between ln{σ/[(A+Bεⁿ)(1+λln d^*)]} and (T-T_ref) at strain rate of 0.05 s^-1

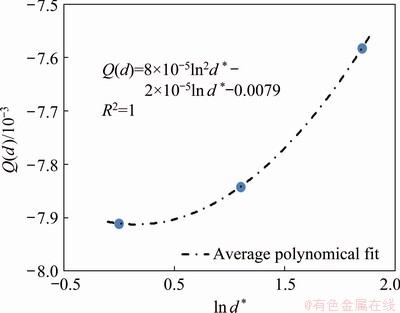
Fig. 8 Variation of Q(d) with initial grain size

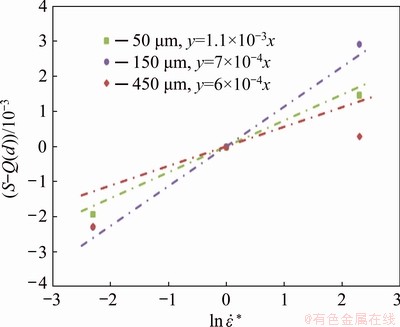
Fig. 9 Correlation of (S-Q(d)) with 

3.3 Correlation of measured and predicted flow stress

The new constitutive model based on modified J-C has been established under different temperature, strain rate, true strain, and initial grain size conditions. Comparison between experimental and calculated flow stress of the developed model is shown in Figs. 10-12, in different processing conditions for initial grain sizes of 50, 150 and 450 μm, respectively. The new constitutive equation utilizing grain size could predict the experimental data of AA1070 aluminum in almost all grain size and deformation conditions. The newly developed modified J-C constitutive equation was verified by comparing the experimental and the predicted flow stress. It can be seen that the predicted flow stress value from the constitutive equation could track the experimental data of AA1070 aluminum under most deformation conditions in different initial grain sizes. Only in some deformation conditions in the initial grain size of 50 μm at 623 K and 723 K and 0.5 s^-1 (as seen in Fig. 10(c)) and also in the initial grain size of 450 μm at 623 K and 0.005 s^-1 and 773 K and 0.5 s^-1 (as seen in Figs. 12(a, c)), an obvious difference between experimental and calculated flow stress data can be observed.

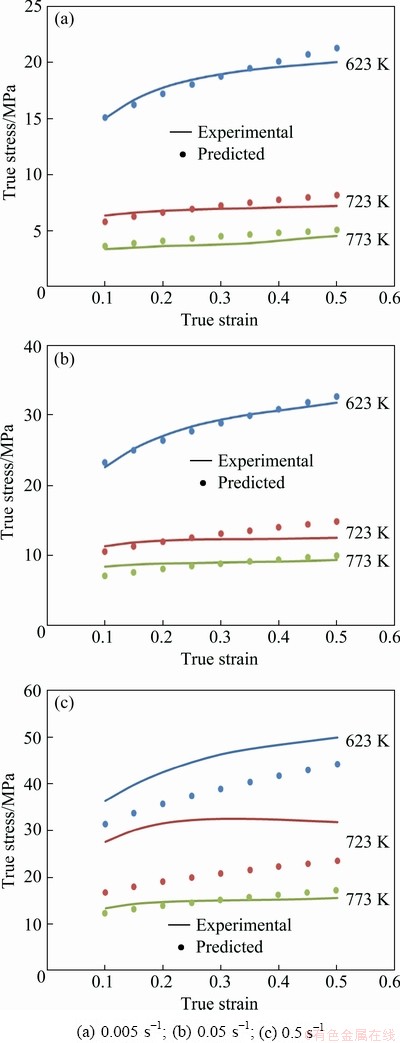
Fig. 10 Comparison between experimental results and predicted data of flow stress using new modified J-C model with initial grain size of 50 μm, at different temperatures and strain rates

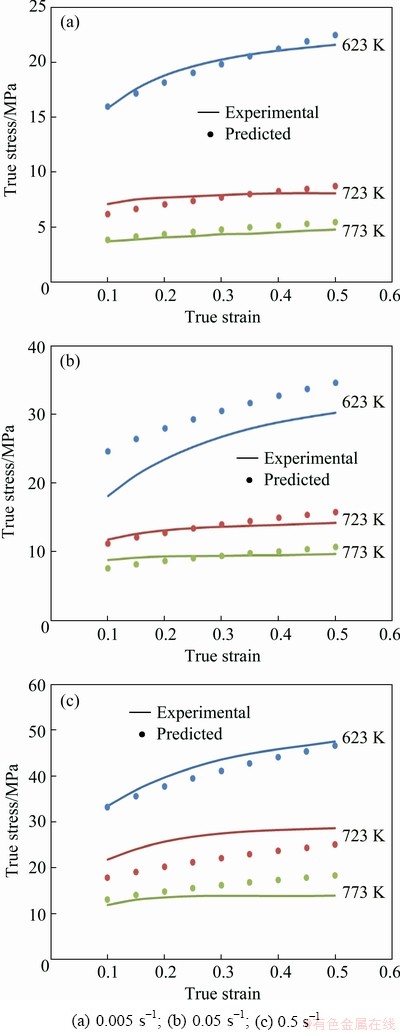
Fig. 11 Comparison between experimental results and predicted data of flow stress using new modified J-C model with initial grain size of 150 μm, at different temperatures and strain rates

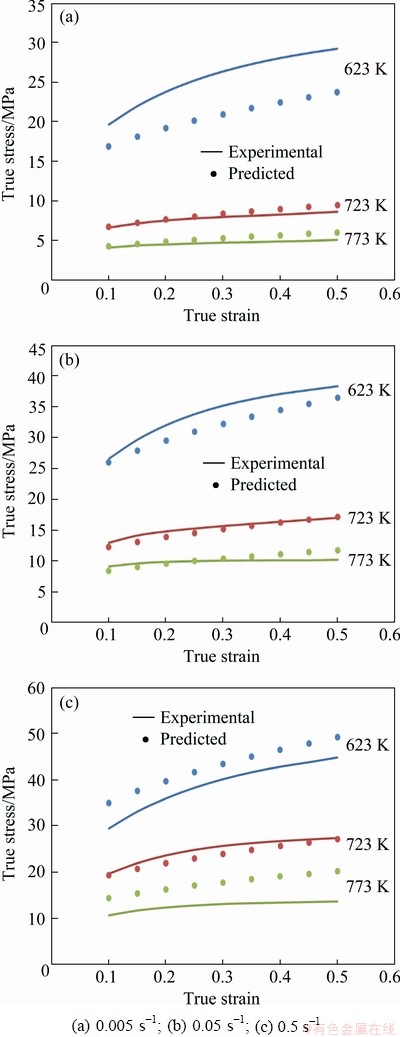
Fig. 12 Comparison between experimental results and predicted data of flow stress using new modified J-C model with initial grain size of 450 μm, at different temperatures and strain rates

The main reason for the difference may be that the response of the flow behavior of metal materials at high temperatures is highly nonlinear. Meanwhile, many factors consisting of initial grain size affecting the flow stress are also nonlinear, which makes the accuracy of the predicted flow stress by the constitutive equations low and the applicable range limited [29,46,47]. LIN and CHEN [47] reported that the predicted flow stress data obtained by the modified J-C constitutive equation were much lower than experimental data at the lower strain. LI et al [48] also reported that some deviation between the experimental and predicted flow stress was observed at the strain rate of 0.01 and 1 s^-1. In the investigation of the flow behavior of 30Cr2Ni4MoV steel at the elevated temperature, the comparisons between the predicted flow stress values by developed constitutive equation and measured ones confirmed that the modified J-C model was valid for predicting the flow stress of 30Cr2Ni4MoV steel and some deviation was observed under some deformation conditions [49].

The predictability of the new modified J-C constitutive equation was quantified in terms of correlation coefficient (R) and average absolute relative error (AARE). The linear relationship between experimental and predicted values is revealed with correlation coefficient (R) and can be expressed as

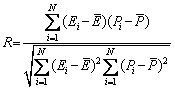               (15)

where 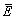and 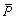are the mean values of experimental and predicted data, respectively. The correlations between experimental flow stress data and predicted data by new modified J-C over a certain range of the strain, strain rate, and temperature with the initial grain sizes of 50, 150, and 450 μm are shown in Fig. 13. It can be seen that the data points in the model lie close to the line. The R values for the new modified J-C model for the initial grain size of 50, 150, and 450 μm are 0.9632, 0.9759, and 0.9692, respectively, and for all conditions, it is 0.9626. Besides, the AARE value obtained for the new modified J-C model for    the initial grain sizes of 50, 150, and 450 μm are 10.71%, 9.88%, and 11.8%, respectively, and for all conditions, it is 10.8%.

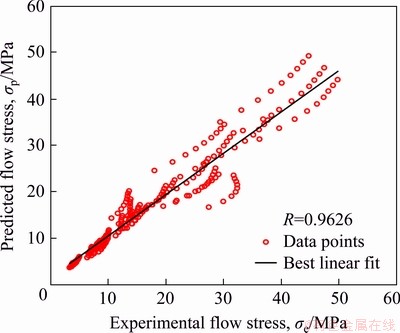
Fig. 13 Relation between experimental data and model-based data of flow stress

The predictability of the developed model is further investigated by calculating relative error:

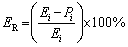                     (16)

The comparison of relative error (RE) between the experimental and model-based flow stress values under all conditions is represented in Fig. 14. The mean relative error for the new modified J-C model is 1.19%.

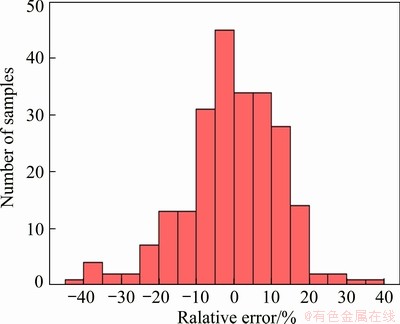
Fig. 14 Relative error of new modified J-C model

4 Conclusions

(1) Variations in initial grain size, strain rate, and deformation temperature affect the flow stress in the hot deformation process of AA1070 aluminum.

(2) The original J-C model takes strain rate, strain, and temperature separately into account and it ignores the influence of the initial grain size of the material. Thus, this is important to modify this equation for considering the effect of grain size on the flow stress behavior. So, inter-relation among stress (σ), strain (ε), strain rate (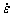), deformation temperature (T), and initial grain size (d) is presented based on a new modified J-C model.

(3) The correlation coefficient values for the new modified J-C model for the initial grain sizes of 50, 150 and 450 μm are 0.9632, 0.9759 and 0.9692, respectively, and for all conditions, it is 0.9626. Besides, The AARE value obtained for the new modified J-C model for the initial grain sizes of 50, 150, and 450 μm are 10.71%, 9.88%, and 11.8%, respectively, and for all conditions, it is 10.8%, with a mean relative error of 1.19%. The modified J-C constitutive equation utilizing initial grain sizes has relatively high accuracy.

References

[1] ROY RK, DAS S. New combination of polishing and etching technique for revealing grain structure of an annealed aluminum (AA1235) alloy [J]. Journal of Materials Science, 2006, 41: 289-292. doi:10.1007/s10853-005-3304-x.

[2] TOTTEN G E, MACKENZIE D S. Handbook of aluminum: Physical metallurgy and processes [M]. Vol. 41. CRC press, 2004. doi:10.5860/choice.41-3468.

[3] LIN Y C, CHEN Ming Song, ZHONG Jue. Prediction of 42CrMo steel flow stress at high temperature and strain rate [J]. Mechanics Research Communications, 2008, 35: 142-150. doi:10.1016/j.mechrescom.2007.10.002.

[4] MANDAL S, RAKESH V, SIVAPRASAD P V, VENUGOPAL S, KASIVISWANATHAN K V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel [J]. Materials Science and Engineering A, 2009, 500: 114-121. doi:10.1016/J. MSEA.2008.09.019.

[5] KHAMEI A A, DEHGHANI K. Modeling the hot- deformation behavior of Ni60wt.%–Ti40wt.% intermetallic alloy [J]. Journal of Alloys and Compounds, 2010, 490: 377-381. doi:10.1016/J.JALLCOM.2009.09.187.

[6] SAMANTARAY D, MANDAL S, BHADURI A K. Constitutive analysis to predict high-temperature flow stress in modified 9Cr-1Mo (P91) steel [J]. Materials & Design, 2010, 31: 981-984. doi:10.1016/J. MATDES.2009.08.012.

[7] ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics- based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61: 1816-1825. doi:10.1063/1.338024.

[8] ZHANG Hong-jian, WEN Wei-dong, CUI Hai-tao, XU Ying. A modified Zerilli-Armstrong model for alloy IC10 over a wide range of temperatures and strain rates [J]. Materials Science and Engineering A, 2009, 527: 328-333. doi: 10.1016/j.msea.2009.08.008.

[9] REZAEI A H R, PARSA M H, BISADI H. Effects of initial grain size on hot deformation behavior of commercial pure aluminum [J]. Materials & Design, 2012, 42: 478-485. doi:10.1016/J.MATDES.2012.06.021.

[10] YANG Yong-biao, ZHANG Zhi-min, LI Xu-bin, WANG Qiang, ZHANG Yan-hui. The effects of grain size on the hot deformation and processing map for 7075 aluminum alloy [J]. Materials & Design, 2013, 51: 592-597. doi:10.1016/J. MATDES.2013.04.034.

[11] BARNETT M R, BEER A G, ATWELL D, OUDIN A. Influence of grain size on hot working stresses and microstructures in Mg-3Al-1Zn [J]. Scripta Materialia, 2004, 51: 19-24. doi:10.1016/J.SCRIPTAMAT.2004.03.023.

[12] YUE Chong-xiang, ZHANG Li-wen, LIAO Shu-lun, GAO Hui-ju. Mathematical models for predicting the austenite grain size in hot working of GCr15 steel [J]. Computational Materials Science, 2009, 45: 462-466. doi:10.1016/J. COMMATSCI.2008.11.003.

[13] BELYAKOV A, TSUZAKI K, MIURA H, SAKAI T. Effect of initial microstructures on grain refinement in a stainless steel by large strain deformation [J]. Acta Materialia, 2003, 51: 847-861. doi:10.1016/S1359-6454(02)00476-7.

[14] MANN G, GRIFFITHS J R, CACERES C H. Hall-Petch parameters in tension and compression in cast Mg-2Zn alloys [J]. Journal of Alloys and Compounds, 2004, 188-191. doi:10.1016/j.jallcom.2003.12.052.

[15] ZHANG Jing, CHEN Bo-quan, ZHANG Bao-xiang. Effect of initial microstructure on the hot compression deformation behavior of a 2219 aluminum alloy [J]. Materials & Design, 2012, 34: 15-21. doi:10.1016/J.MATDES.2011.07.061.

[16] BEER A G, BARNETT M R. Influence of initial microstructure on the hot working flow stress of Mg-3Al-1Zn [J]. Materials Science and Engineering A, 2006, 423: 292-299. doi:10.1016/J.MSEA.2006.02.041.

[17] JAIN A, DUYGULU O, BROWN D W, TOME C N, AGNEW S R. Grain size effects on the tensile properties and deformation mechanisms of a magnesium alloy AZ31B sheet [J]. Materials Science and Engineering A, 2008, 486: 545-555. doi:10.1016/J.MSEA.2007.09.069.

[18] PETCH N J. The cleavage strength of polycrystals [J]. Journal of the Iron and Steel Institute, 1953, 174: 25-28.

[19] MEYERS M A, VOHRINGER O, LUBARDA V A. The onset of twinning in metals: A constitutive description [J]. Acta Materialia, 2001, 49: 4025-4039. doi:10.1016/S1359- 6454(01)00300-7.

[20] BARNETT M R, KESHAVARZ Z, BEER A G, ATWELL D. Influence of grain size on the compressive deformation of wrought Mg-3Al-1Zn [J]. Acta Materialia, 2004, 52: 5093-5103. doi:10.1016/J.ACTAMAT.2004.07.015.

[21] LIN Y C, LUO Shun-cun, JIANG Xing-you, TANG Yi, CHEN Ming-song. Hot deformation behavior of a Sr-modified Al-Si-Mg alloy: Constitutive model and processing maps [J]. Transactions of Nonferrous Metals Society of China, 2018, 28: 592-603. doi:10.1016/S1003- 6326(18)64692-8.

[22] LI Jian-bo, LIU Yong, WANG Yan, LIU Bin, LU Bin, LIANG Xiao-peng. Constitutive equation and processing map for hot compressed as-cast Ti-43Al-4Nb-1.4W-0.6B alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 3383-3391. doi:10.1016/S1003-6326(13) 62878-2.

[23] DAI Qing-song, DENG Yun-lai, TANG Jian-guo, WANG Yu. Deformation characteristics and strain-compensated constitutive equation for AA5083 aluminum alloy under hot compression [J]. Transactions of Nonferrous Metals Society of China, 2019, 29: 2252-2261. doi:10.1016/S1003-6326(19) 65131-9.

[24] GAN Chun-lei, ZHENG Kai-hong, QI Wen-jun, WANG Meng-jun. Constitutive equations for high temperature flow stress prediction of 6063 Al alloy considering compensation of strain [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 3486-3491. doi:10.1016/S1003-6326(14) 63492-0.

[25] GORDON J, COOK W H. A constitutive model and data for metals subjected to large strains high strain rates and high temperatures [C]//International Symposium on Ballistics. 1983: 541-547.

[26] CHENG Yong-qi, ZHANG Hui, CHEN Zhen-hua, XIAN Kui-feng. Flow stress equation of AZ31 magnesium alloy sheet during warm tensile deformation [J]. Journal of Materials Processing Technology, 2008, 208: 29-34. doi: 10.1016/j.jmatprotec.2007.12.095.

[27] SLOOFF F A, ZHOU J, DUSZCZYK J, KATGERMAN L. Constitutive analysis of wrought magnesium alloy Mg-Al4-Zn1 [J]. Scripta Materialia, 2007, 57: 759-762. doi: 10.1016/j.scriptamat.2007.06.023.

[28] REZAEI ASHTIANI H R, PARSA M H, BISADI H. Effects of initial grain size on hot deformation behavior of commercial pure aluminum [J]. Materials & Design, 2012, 42: 478-485. doi:10.1016/j.matdes.2012.06.021.

[29] CAI Jun, WANG Kuai-she, ZHAI Peng, LI Fu-guo, YANG Jie. A modified Johnson-Cook constitutive equation to predict hot deformation behavior of Ti-6Al-4V alloy [J]. Journal of Materials Engineering and Performance, 2015, 24: 32-44. doi:10.1007/s11665-014-1243-x.

[30] CHE Jiang-tao, ZHOU Tian-feng, LIANG Zhi-qiang, WU Jun-jie, WANG Xi-bin. An integrated Johnson–Cook and Zerilli–Armstrong model for material flow behavior of Ti-6Al-4V at high strain rate and elevated temperature [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2018, 40: 1-10. doi:10.1007/s40430-018- 1168-7.

[31] KHAN A S, ZHANG H Y, TAKACS L. Mechanical response and modeling of fully compacted nanocrystalline iron and copper [J]. International Journal of Plasticity, 2000, 16: 1459-1476. doi:10.1016/ S0749-6419(00)00023-1.

[32] KHAN A S, SUH Y S, CHEN X, TAKACS L, ZHANG H Y. Nanocrystalline aluminum and iron: Mechanical behavior at quasi-static and high strain rates and constitutive modeling [J]. International Journal of Plasticity, 2006, 22: 195-209. doi:10.1016/j.ijplas.2004. 07.008.

[33] FARROKH B, KHAN A S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling [J]. International Journal of Plasticity, 2009, 25: 715-732. doi:10.1016/j.ijplas. 2008.08.001.

[34] LI Kuo, PAN Qing-lin, LI Rui-shi, LIU Shu-hui, HUANG Zhi-qi, HE Xin. Constitutive modeling of the hot deformation behavior in 6082 aluminum alloy [J]. Journal of Materials Engineering and Performance, 2019, 28: 981-994. doi:10.1007/s11665-019-3873-5.

[35] SANI S A, EBRAHIMI G R, VAFAEENEZHAD H, KIANI-RASHID A R. Modeling of hot deformation behavior and prediction of flow stress in a magnesium alloy using constitutive equation and artificial neural network (ANN) model [J]. Journal of Magnesium and Alloys, 2018, 6: 134-144. doi:10.1016/j.jma.2018.05.002.

[36] REZAEI ASHTIANI H R, SHAHSAVARI P. A comparative study on the phenomenological and artificial neural network models to predict hot deformation behavior of AlCuMgPb alloy [J]. Journal of Alloys and Compounds, 2016, 687: 263-273. doi:10.1016/j.jallcom.2016.04.300.

[37] WANG Xiang-dong, PAN Qing-lin, XIONG Shang-wu, LIU Li-li, SUN Yuan-wei, WANG Wei-yi. Prediction on hot deformation behavior of spray-formed 7055 aluminum alloy via phenomenological models [J]. Transactions of Nonferrous Metals Society of China, 2018, 28: 1484-1494. doi:10.1016/S1003-6326(18)64789-2.

[38] LI Peng-wei, LI Hui-zhong, HUANG Lan, LIANG Xiao-peng, ZHU Ze-xiao. Characterization of hot deformation behavior of AA2014 forging aluminum alloy using processing map [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1677-1688. doi:10.1016/S1003- 6326(17)60190-0.

[39] HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena [J]. 2nd Ed. Elsevier, 2004. doi:10.1016/B978-008044164-1/50017-7.

[40] HAN Ying, LIU Gui-wu, ZOU De-ning, LIU Rong, QIAO Guan-jun. Deformation behavior and microstructural evolution of as-cast 904L austenitic stainless steel during hot compression [J]. Materials Science and Engineering A, 2013, 565: 342-350. doi:10.1016/J.MSEA.2012.12.043.

[41] SAMANTARAY D, MANDAL S, PHANIRAJ C, BHADURI A K. Flow behavior and microstructural evolution during hot deformation of AISI Type 316 L(N) austenitic stainless steel [J]. Materials Science and Engineering A, 2011, 528: 8565-8572. doi: 10.1016/j.msea.2011.08.012.

[42] VERLINDEN B, DRIVER J, SAMAJDAR I, DOHERTY R D. Thermo-mechanical processing of metallic materials. Vol. 11: Pergamon materials series [M]. Elsevier, 2007. doi:10.1016/S1470-1804(07)80018-6.

[43] SUN Hui-li, ZHANG Yi, VOLINSKY A A, WANG Bing-jie, TIAN Bao-hong, SONG Ke-xing. Effects of Ag addition on hot deformation behavior of Cu-Ni-Si alloys [J]. Advanced Engineering Materials, 2017, 19: 1600607. doi: 10.1002/ adem.201600607.

[44] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21: 31-48. doi:10.1016/0013- 7944(85)90052-9.

[45] LIN Y C, CHEN Xiao-min, LIU Ge. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel [J]. Materials Science and Engineering A, 2010, 527: 6980-6986. doi:10.1016/J.MSEA. 2010.07.061.

[46] CAI Jun, WANG Kuai-she, ZHAI Peng, LI Fu-guo, YANG Jie. A modified Johnson-Cook constitutive equation to predict hot deformation behavior of Ti-6Al-4V alloy [J]. Journal of Materials Engineering and Performance, 2015, 24: 32-44. doi:10.1007/s11665-014-1243-x.

[47] LIN Y C, CHEN Xiao-min. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials & Design, 2011, 32: 1733-1759. doi:10.1016/j.matdes.2010.11.048.

[48] LI Hong-ying, WANG Xiao-feng, WEI Dong-dong, HU Ji-dong, LI Yang-hua. A comparative study on modified Zerilli-Armstrong, Arrhenius-type and artificial neural network models to predict high-temperature deformation behavior in T24 steel [J]. Materials Science and Engineering A, 2012, 536: 216-222. doi:10.1016/j.msea.2011.12.108.

[49] WANG Y P, HAN Chun-jie, WANG Can, LI Shi-ke. A modified Johnson-Cook model for 30Cr2Ni4MoV rotor steel over a wide range of temperature and strain rate [J]. Journal of Materials Science, 2011, 46: 2922-2927. doi:10.1007/ s10853-010-5167-z.

利用晶粒尺寸构建本构方程模拟AA1070铝的热变形行为

H. R. REZAEI ASHTIANI, A. A. SHAYANPOOR

School of Mechanical Engineering, Arak University of Technology, Arak, 38135-1177, Iran

摘  要：对原有Johnson-Cook本构模型中的项进行修正，提出一种新的现象学的、基于经验的本构模型。该模型可用于描述和预测具有不同初始晶粒尺寸的AA1070铝在热加工过程中的流变应力。该模型考虑热软化、应变速率硬化、应变硬化、初始晶粒尺寸及其相互影响，能够正确模拟具有不同应变、应变速率和初始晶粒尺寸AA1070铝的高温行为。通过压缩试验测试的AA1070铝的热流变行为，温度范围为623~773 K，应变速率为0.005~0.5 s^-1，初始晶粒尺寸为50~450 μm。 结果表明，初始晶粒尺寸对AA1070铝的流变行为有显著影响。通过相关系数(R)、平均绝对相对误差(AARE)、相对误差评估模型的可预测性。结果表明，新模型预测的具有不同初始晶粒尺寸材料的流变应力与实验值完全一致，平均相对误差为1.19%，证实新修正的Johnson-Cook关系能准确估计考虑初始晶粒尺寸时AA1070铝的热流变应力。

关键词：本构方程；修正的Johnson-Cook模型；初始晶粒尺寸；流变应力；热变形；AA1070铝

 (Edited by Bing YANG)

Corresponding author: H. R. REZAEI ASHTIANI; Tel: +98-86-33400671; Fax: +98-861-3670020; E-mail: hr_rezaei@arakut.ac.ir,

 hrr.Ashtiani@gmail.com

DOI: 10.1016/S1003-6326(21)65500-0

1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press