J. Cent. South Univ. (2016) 23: 233-239

DOI: 10.1007/s11771-016-3066-4

Effects of friction variability on isolation performance of rolling-spring systems

WEI Biao(魏标)^{1, 2}, WANG Peng(王鹏)¹, YANG Tian-han(杨添涵)¹,

DAI Gong-lian(戴公连)^{1, 2}, JIANG Li-zhong(蒋丽忠)^{1, 2}, WEN Ying(文颖)¹

1. School of Civil Engineering, Central South University, Changsha 410075, China;

2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410004, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: By taking a rolling-spring isolation system as the study object, the effects of the non-uniform distribution of rolling friction coefficient on its isolation performance were analyzed by a compiled computer program. The results show that the errors associated with the structural maximum relative displacement, acceleration and residual displacement due to ignoring the friction variability sequentially grow. This rule is weakened by the spring action, however, the unreasonable spring constant will cause sympathetic vibration. Under the condition of large friction variability, in the calculation of the structural maximum relative displacement and acceleration, the friction variability should be considered. When the structural residual displacement is concerned, the variability of rolling friction coefficient should be fully considered regardless of the friction variability.

Key words: rolling-spring structure; seismic isolation; rolling friction; seismic performance

1 Introduction

Seismic damage has been commonly observed in general structures [1–3]. Many kinds of isolation devices have been considered as an effective method to mitigate the seismic damage and thus are widely used all over the world. As to obtain the better isolation performance, many researchers have paid attention to a new rolling-based isolation method in recent years [4]. In India, JANGID and LONDHE [5] developed a theoretical formulation to obtain seismic responses of a multistory building supported by elliptical rolling rods in 1998, which were quite effective in reducing the seismic response of the system without undergoing large base displacements. In 2000, JANGID [6] investigated the stochastic response, under the earthquake motion, of flexible multistory shear type buildings isolated by rolling rods with a re-centering device, indicating that the rolling rods were quite effective in reducing the stochastic response of the structure against earthquake excitation. In USA, OU et al [7] proposed a roller seismic isolation bearing for use in highway bridges in 2010, which utilized a rolling mechanism to achieve seismic isolation and had zero post-elastic stiffness under horizontal ground motions, and a self-centering capability and unique friction devices for supplemental energy dissipation. After investigating seismic behaviors of the proposed bearing through parametric studies, they suspected that there were something wrong with the calculation method in AASHTO Specifications and suggested further investigations [7–8]. In Portugal, GUERREIRO et al [9] carried out a seismic test and a numerical modeling of a rolling-ball isolation system to protect some light structures in 2007, and the results showed an effective reduction of the acceleration levels induced in the isolated structures. In Japan, KURITA et al [10] developed a new device of reduction for seismic response using friction force, and the peak acceleration amplitude on this system was decreased by about 50%–90% over the input waves. In 2012, NANDA et al [11] in India considered that the base isolation in the form of pure friction (P-F), among all other isolation methods developed so far, was the simplest one, which could be easily applied to low cost brick masonry buildings. Furthermore, the P-F isolation was one of the best alternatives for reducing the earthquake energy transmission to the superstructure during strong earthquakes.

In these studies, the seismic force of structure transferred from the ground motion was controlled to be a small value by setting the rolling friction isolation device, which was usually the dynamic friction force. Although the rolling friction isolation device can avoid the seismic damage caused in structures, the induced displacement may be very large and difficult to control [12]. Therefore, the spring can be added to the rolling friction isolation device to decrease the seismic relative displacement and residual displacement. In 2014, WEI et al [13] investigated the calculation methods of a rolling-spring isolation system, and identified that the optimized isolation performance could be obtained by reasonably combining the spring device and the rolling friction device. They confirmed the perfect isolation efficiency of rolling-based isolation methods; however, they generally assumed the rolling friction coefficient as a fixed value to simplify the calculation process as well as other studies [14–15], i.e., the distribution of the rolling friction coefficient on the whole contact surface was absolutely uniform, which was opposite to the reality. In fact, there are different variabilities of rolling friction coefficient on the contact surfaces according to their current construction levels. Hence, it is desirable to analyze whether the results, including the structural acceleration, relative displacement and residual displacement, based on the original assumption of uniform friction are safe, and what the corresponding errors are.

In this work, by taking a rolling-spring isolation system as the study object, the effects of different non- uniform distributions of rolling friction coefficient on its isolation performance under different earthquake motions were systematically analyzed by a compiled computer program. The calculation errors of the rolling- spring isolation system ignoring friction variability were summarized, which was useful for the potential improvement on the isolation system in the future.

2 Calculation process

2.1 Structural model

In 2014, WEI et al [13] compiled a computer program to investigate the calculation methods of a rolling-spring isolation system. In this work, this computer program was used to analyze the seismic performance of the rolling-spring isolation system, as shown in Fig. 1, and the isolated structure was built as one rigid body since the stiffness of isolation device was much less than that of structure [13]. The structure mass was set to be 300 t in this work, and the spring constants adopted were 200, 400, 600, 800 and 1000 kN·s/m, respectively.

In Fig. 2, as for the average rolling friction coefficient of 0.005 on the contact surface of Fig. 1, there were three cases of rolling friction coefficient distribution:

Case 1 (uniform friction distribution): The rolling friction coefficient, along with different positions of contact surface, didn’t change, which was consistent with the traditional assumptions that the rolling friction coefficient was simplified as a fixed value whether the friction distribution on the contact surface was uniform or not.

Fig. 1 Rolling-spring isolation system

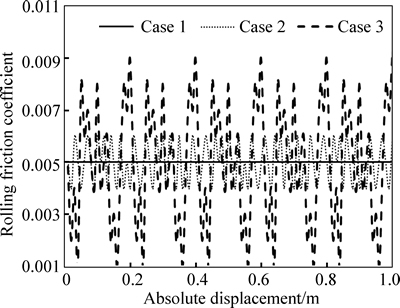
Fig. 2 Three cases of rolling friction coefficient distribution (average value: 0.005)

Case 2 (slightly non-uniform friction distribution): As the position of contact surface changed, the rolling friction coefficient slightly varied around its mean value and the variation range was from –0.001 to 0.001, which corresponded to the perfect construction level.

Case 3 (significantly non-uniform friction distribution): In terms of the rolling friction coefficient on the poorly constructed contact surface, there was a wide range of fluctuation around the average rolling friction coefficient and the variation range was from –0.004 to 0.004.

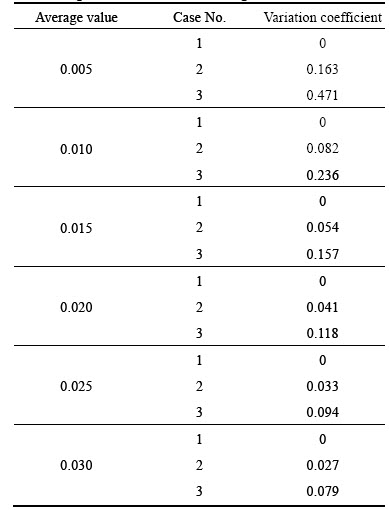
In this work, for the contact surface of the isolated structure in Fig. 1, six average rolling friction coefficients, including 0.005, 0.010, 0.015, 0.020, 0.025 and 0.030, were adopted. And for each average rolling friction coefficient, there were three cases of friction distribution with the same variation range as shown in Fig. 2. Hence, eighteen cases were obtained in Table 1.

Table 1 Eighteen distributions of rolling friction coefficient

2.2 Earthquake input

As for each elastic response spectrum for soil profile I, II, III, and IV in Chinese criteria (JTJ 004—89) [16], one accelerogram was generated by Simqke procedure to be the ground motion input of the computer program. In the latter analysis, each accelerogram’s peak ground accelerations (PGAs) were adjusted to be 0.2g, 0.4g, 0.6g and 0.8g, respectively.

2.3 Calculation cases

In the foregoing descriptions, there were 5 spring constants, 6 average rolling friction coefficients (18 friction distributions), 4 soil profile accelerograms and  4 PGAs. And totally 1440 cases were generated for further calculation.

In terms of each combination corresponding to Cases 2 and 3 of each average rolling friction coefficient, the real spatial distribution of rolling friction coefficient was strictly considered in the calculation process, and the ratios of their results to the counterpart of Case 1 were analyzed to express the effects of the friction variability on the seismic performance. The ratios of their results included the structural maximum acceleration, maximum relative displacement and residual displacement. As for each result, the influence factors included the variability of rolling friction coefficient, damping constant and different ground motions.

3 Structural maximum acceleration

3.1 Effects of friction variability on structural maximum acceleration

Figure 3(a) shows the influence of the variability of rolling friction coefficient on the structural maximum acceleration. As the friction variability increases, the range of the ratios of the calculation result of the non-uniform friction cases to that of the uniform friction cases becomes wider. The maximum ratio even reaches 1.47 when the variability of rolling friction coefficient is 0.471. Under this condition, if the rolling friction coefficient is simplified as a mean value, ignoring its variability, to calculate the seismic response of the isolation system, the structural maximum acceleration is 47% less than the exact one. Hence, it is necessary to fully consider the friction variability when calculating the structural maximum acceleration.

For the isolation system in Fig. 1, the maximum acceleration (A_max) of the structure is [μg+K(d_e–d_s)/m]. As the rolling friction coefficient μ at any position of the contact surface varies around its mean value of μ_av due to the friction variability, the structural acceleration within any time step changes around [μ_avg+K(d_e–d_s)/m]. As aresult, the structural maximum acceleration of [μ_maxg+ K(d_e–d_s)/m] changes around [μ_avg+K(d_e–d_s)/m]. Moreover, the larger the friction variability is, the wider the range of the ratio of [μ_maxg+K(d_e–d_s)/m] to [μ_avg+ K(d_e–d_s)/m] should be, which is validated in Fig. 3(a).

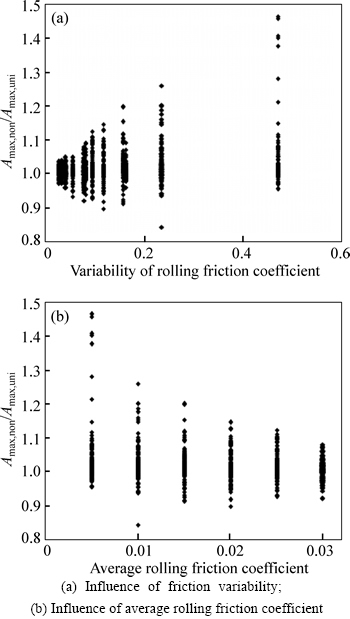
Fig. 3 Effects of rolling friction coefficient on structural maximum acceleration:

According to the current construction level of contact surface, the variable amplitude of the rolling friction coefficient can be controlled within a certain range regardless of its mean value. Hence, as the average rolling friction coefficient increases, the corresponding variability and the ratio of [μ_maxg+K(d_e–d_s)/m] to [μ_avg+ K(d_e–d_s)/m], as shown in Fig. 3(b), both become less.

3.2 Effects of spring constant on structural maximum acceleration

In theory, the rule in Section 3.1 will be weakened by the following phenomena:

(1) If μ increases, v_s will increase rapidly, resulting in the decrease of (v_e–v_s) and (d_e–d_s). Hence, the variable trends of μg is opposite to K(d_e–d_s)/m, which decreases the increment of [μg+K(d_e–d_s)/m].

(2) If μ decreases, the variable trends of μg is also opposite to K(d_e–d_s)/m, which then decreases the reduction of [μg+K(d_e–d_s)/m].

Therefore, in Fig. 4, as the spring constant increases, the range of the ratios of the calculation result of the non-uniform friction cases to that of the uniform friction cases becomes narrower except a few special points. These special points can be explained by WEI et al [13]. As the spring becomes stronger, the isolation structure tends to be the traditional elastic isolation system. And when the rolling friction coefficient μ at any position of the contact surface varies around its mean value of μ_av due to the friction variability, the structure vibration period may be close to some periodic components of earthquake. Therefore, it is reasonable that there are some fluctuations for the acceleration ratios, as shown in Fig. 4.

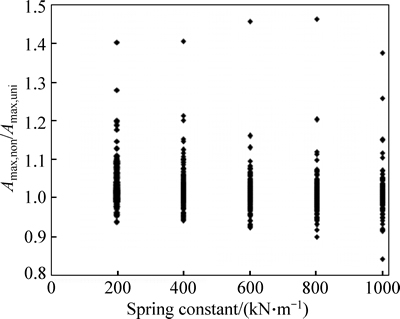
Fig. 4 Effects of spring constant on structural maximum acceleration

3.3 Effects of different ground motions on structural maximum acceleration

Based on the mechanics, the uniform motion in the same direction can strengthen the spring action and weaken the influence of friction variability. This trend is obtained by the following two cases:

(1) As the earthquake soil profile increases, the duration of the ground moving towards the same direction becomes larger.

(2) The increasing of PGA indicates that the moving displacement of the ground during the same time increases.

Under these two conditions, the effects of the friction variability on the structural maximum acceleration decreases. Therefore, in Figs. 5(a) and (b), as the earthquake soil profile number and PGA increase, the overall rules are that the ratios of the structural maximum acceleration of the non-uniform friction cases to that of the uniform friction cases decrease.

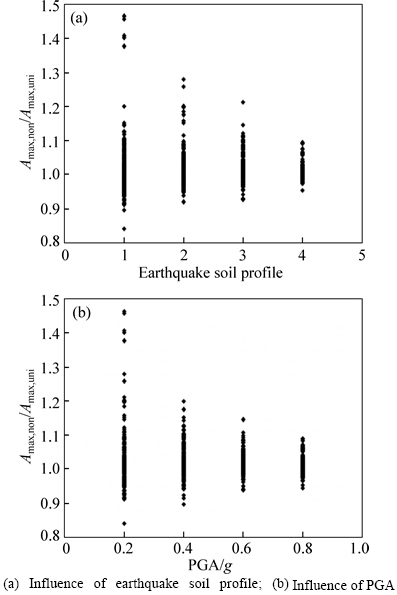
Fig. 5 Effects of ground motions on structural maximum acceleration:

4 Structural maximum relative displacement

4.1 Effects of friction variability on structural maximum relative displacement

Aiming at all cases in Section 2.3, Fig. 6(a) shows that the range of the ratio of the structural maximum relative displacement (D_max) corresponding to the non- uniform friction cases to that of the uniform friction cases becomes wider as the friction variability increases. When the variability of rolling friction coefficient is 0.471, the maximum ratio reaches 1.4, i.e., the structural maximum relative displacement calculated by ignoring friction variability is 40% less than the exact one. Hence, when calculating the structural maximum relative displacement, it is better to consider the friction variability to avoid unsafe results.

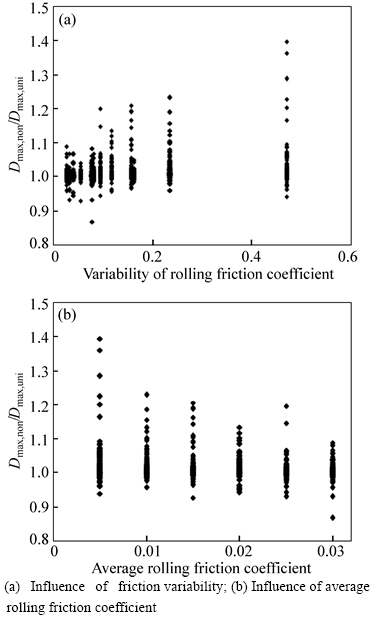
Fig. 6 Effects of rolling friction coefficient on structural maximum relative displacement:

In Fig. 1, when the ground velocity v_e is larger than the structural velocity, the structural acceleration [μg+K(d_e–d_s)/m] makes the structure have the tendency of moving forward, and there are two possibilities:

(1) Under the condition that the moving structure is on the left of its original position: if the rolling friction coefficient μ on the contact surface increases, the structural acceleration [μg+K(d_e–d_s)/m] will increase to decrease the structural relative displacement; otherwise, the structural relative displacement will increase.

(2) If the moving structure is on the right of its original position, the structural relative displacement will change in a direction opposite to Condition (1) along with the increase or decrease of the rolling friction coefficient on the contact surface.

As for the cases of v_e=v_s and v_es, the similar results are obtained. In summary, the variability of rolling friction coefficient can increase or decrease the structural relative displacement under different conditions. And as the friction variability increases, its influence degree will be more significant, resulting in a wider range of the displacement ratio, as shown in Fig. 6(a).

For the general contact surface construction, as the average rolling friction coefficient increases, its friction variability decreases, and thus the corresponding range of the displacement ratios in Fig. 6(b) becomes narrower.

4.2 Effects of spring constant on structural maximum relative displacement

Based on the discussion in Section 3.2, the spring action can weaken the influence of the friction variability on the structural acceleration and thus the structural relative displacement. Hence, in Fig. 7, as the spring constant increases, the range of the ratios of the calculation result of the non-uniform friction cases to that of the uniform friction cases becomes narrower mostly.

A few special points also exist in Fig. 7 since there are some sympathetic vibrations. As the spring becomes stronger, the structure vibration period may be close to some periodic component of earthquake, resulting in the sympathetic vibrations. The phenomenon is obvious when the average rolling friction coefficient is little and the corresponding variability is large.

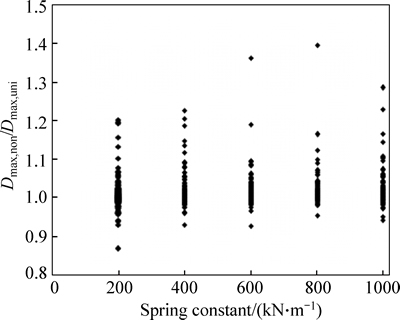
Fig. 7 Effects of spring constant on structural maximum relative displacement

4.3 Effects of different ground motions on structural maximum relative displacement

As the more uniform motion in the same direction, caused by the increasing of the earthquake soil profile number and PGA, can strengthen the spring action and weaken the influence of friction variability, the displacement ratios in Figs. 8(a) and (b) decrease as the earthquake soil profile number and PGA increase.

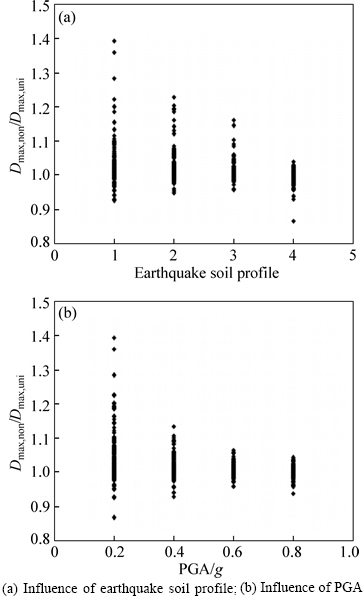
Fig. 8 Effects of ground motions on structural maximum relative displacement:

5 Structural residual displacement

5.1 Effects of friction variability on structural residual displacement

Because the structural residual displacement (D_res) is just a special relative displacement when the structure stops moving, the effects of the friction variability on the structural relative displacement will naturally influence the structural residual displacement. In addition, as the rolling friction prevents the moving of the structure and makes the structure accommodate itself to any place, the structural motion direction, after the ground motion just stops, will also influence the structural residual displacement:

(1) If the structure moves away from the original position, the structural residual displacement will change opposite to the variation trends of the rolling friction coefficient.

(2) Otherwise, the structural residual displacement will change according to the variation trends of the rolling friction coefficient.

The interaction of the above mentioned effects of the friction variability results in the wide range of the ratios of the structural residual displacement corresponding to the non-uniform friction cases to that of the uniform friction cases, as shown in Fig. 9(a). The range is much wider than that of Fig. 6, and has many special points. A special point even reaches 29, which indicates that the calculated structural residual displacement is 2900% less than the exact one if rolling friction coefficient is simplified as a mean value, ignoring its variability, to calculate the seismic response of the isolation system. Hence, it has to fully consider the friction variability when calculating the structural residual displacement. Any simplification of friction distribution will possibly cause significant errors.

As the mean value of rolling friction coefficient increases, its friction variability and the corresponding range of the ratios in Fig. 9(b) are both reduced. However, the maximum ratio, associated with the average rolling friction coefficient of 0.03, still reaches 8.0.

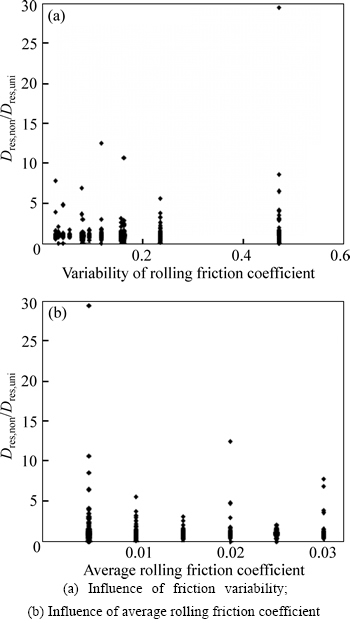
Fig. 9 Effects of rolling friction coefficient on structural residual displacement:

5.2 Effects of spring constant on structural residual displacement

The stronger spring action makes the structure tend to sympathetically vibrate, while the increasing or decreasing of μ will change the vibration period of the isolation system to be close to or away from some periodic components of earthquake and thus change the conditions of the potential sympathetic vibrations. As a result, as the spring constant increases, there is no definite trend for the ratios of the structural residual displacement of the non-uniform friction cases to that of the uniform friction cases. The corresponding figures are not given here due to space limitations.

5.3 Effects of different ground motions on structural residual displacement

As neither the earthquake soil profile nor PGA has the function of restoring the structure to the original position, they don’t have obvious influence on the range of the ratios of the structural residual displacement of the non-uniform friction distribution cases to that of the uniform friction distribution cases, and the corresponding useless figures are not presented here.

6 Conclusions

1) As for the cases of small friction variability, the structural maximum relative displacement and acceleration can be calculated ignoring non-uniform friction distribution; however, in the calculation process of the structural residual displacement, the influence of friction variability has to be fully considered. When the variability of rolling friction coefficient is large, the influence of the non-uniform friction distribution should be fully considered to obtain the exact and safe results for all kinds of the structural seismic responses.

2) The errors associated with the structural maximum relative displacement, acceleration and residual displacement sequentially grow for the same friction variability. This rule is weakened by the spring action; however, the unreasonable spring constant will cause sympathetic vibration. The stronger spring action makes the structure tend to sympathetically vibrate, while the increase or decrease of rolling friction coefficient will change the vibration period of the isolation system to be close to or away from some periodic components of earthquake and thus change the conditions of the potential sympathetic vibrations. The phenomenon is obvious when the spring is strong, the average rolling friction coefficient is little and the corresponding variability is large.

3) Previously, many similar isolation systems are designed ignoring the variability of rolling friction coefficient. Based on this work, however, design results of these systems may be unsafe and need to be re-examined. Furthermore, in the future, it is desirable to carry out more extensive researches on the effects of non-uniform distribution of rolling friction coefficient on other isolation systems with friction action.

References

[1] WEI Biao, XIA Ye, LIU Wei-an. Lateral vibration analysis of continuous bridges utilizing equal displacement rule [J]. Latin American Journal of Solids and Structures, 2014, 11(1): 75–91.

[2] YAN Bin, DAI Gong-lian. Seismic pounding and protection measures of simply-supported beams considering interaction between continuously welded rail and bridge [J]. Structural Engineering International, 2013, 23(1): 61–67.

[3] WEI Biao．Study of the applicability of modal pushover analysis on irregular continuous bridges [J]. Structural Engineering International, 2011, 21(2): 233–237.

[4] WEI Biao, CUI Rui-bo, DAI Gong-lian. Seismic performance of a rolling-damper isolation system [J]. Journal of Vibroengineering, 2013, 15(3): 1504–1512.

[5] JANGID R S, LONDHE Y B. Effectiveness of elliptical rolling rods for base isolation [J]. Journal of Structural Engineering, 1998, 124(4): 469–472.

[6] JANGID R S. Stochastic seismic response of structures isolated by rolling rods [J]. Engineering Structures, 2000, 22(8): 937–946.

[7] OU Y C, SONG J W, LEE G C. A parametric study of seismic behavior of roller seismic isolation bearings for highway bridges [J]. Earthquake Engineering and Structure Dynamics, 2010, 39(5): 541–559.

[8] LEE G C, OU Y C, NIU T C, SONG J W, LIANG Z. Characterization of a roller seismic isolation bearing with supplemental energy dissipation for highway bridges [J]. Journal of Structural Engineering, 2010, 136(5): 502–510.

[9] GUERREIRO L, AZEVEDO J, MUHR A H. Seismic tests and numerical modeling of a rolling-ball isolation system [J]. Journal of Earthquake Engineering, 2007, 11(1): 49–66.

[10] KURITA K, AOKI S, NAKANISHI Y, TOMINAGA K, KANAZAWA M. Fundamental characteristics of reduction system for seismic response using friction force [J]. Journal of Civil Engineering and Architecture, 2011, 5(11): 1042–1047.

[11] NANDA R P, AGARWAL P, SHRIKHANDE M. Base isolation system suitable for masonry buildings [J]. Asian Journal of Civil Engineering (Building and Housing), 2012, 13(2): 195–202.

[12] MONFARED H, SHIRVANI A, NWAUBANI S. An investigation into the seismic base isolation from practical perspective [J]. International Journal of Civil and Structural Engineering, 2012, 3(3): 451–463.

[13] WEI Biao, DAI Gong-lian, WEN Ying, XIA Ye. Seismic performance of an isolation system of rolling friction with spring [J]. Journal of Central South University, 2014, 21(4): 1518–1525.

[14] YAN Bin, DAI Gong-lian, ZHANG Hua-ping. Beam-track interaction of high-speed railway bridge with ballast track [J]. Journal of Central South University, 2012, 19(5): 1447–1453.

[15] WANG Ying-jie, WEI Qing-chao, SHI Jin, LONG Xu-you. Resonance characteristics of two-span continuous beam under moving high speed trains [J]. Latin American Journal of Solids and Structures, 2010, 7(2): 185–199.

[16] Standard of the Ministry of Communications of China. JTJ004—89, Specifications of earthquake resistant design for highway engineering [S]. Beijing: China Communications Press, 1989. (in Chinese)

(Edited by YANG Bing)

Foundation item: Projects(51308549, 51378504, 51478475) supported by the National Natural Science Foundation of China; Project(2015JJ3159) supported by the Natural Science Foundation of Hunan Province, China; Project(2015CX006) supported by the Innovation-driven Plan in Central South University, China

Received date: 2014-05-20; Accepted date: 2015-09-23

Corresponding author: WEI Biao, Associate Professor, PhD; Tel: +86–14789706432; E-mail: weibiaocsu@163.com