Trans. Nonferrous Met. Soc. China 30(2020) 236-248

Adsorption behavior of Sb(III) in single and binary Sb(III)-Fe(II) systems on cationic ion exchange resin: Adsorption equilibrium, kinetic and thermodynamic aspects

F. MOGHIMI¹, A. H. JAFARI², H. YOOZBASHIZADEH³, M. ASKARI³

1. Department of Materials Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran;

2. Department of Materials Science and Engineering, College of Engineering, Shahid Bahonar University of Kerman, Kerman, Iran;

3. Department of Materials Science and Engineering, Sharif University of Technology, Tehran, Iran

Received 13 December 2018; accepted 18 October 2019

Abstract: The present study dealt with the mechanism of competitive adsorption of Sb(III) and Fe(II) ions from a copper-containing aqueous solution on Purolite S957, a commercially available cationic ion-exchange adsorbent. Experiments were conducted using aqueous copper sulfate solutions containing either single or conjoint ions, using both sedentary and batch adsorption techniques to ascertain the sensitivity of the adsorption process to variation in pH, mass of resin, contact time, and temperature as well as establishing the optimal range of variables for maximum ion removal. The data from single ion adsorption tests were fitted by non-linear regression techniques to Henry, Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich isotherm models. Freundlich isotherm for Sb(III) and Freundlich and Henry models for Fe(II) solutions best express the adsorption equilibrium data; while for binary ion electrolytes, the extended Freundlich model fitted the data satisfactorily. The kinetic model adequately describing adsorption was shown to be the pseudo-first-order, underscoring the dominant role of physical adsorption playing in the process. Thermodynamic parameters for the adsorption process reveal differences in the Sb(III) adsorption mechanism from single ion and Sb(III)-Fe(II) containing electrolytes. The adsorption of Sb(III) alone is endothermic, whereas the process becomes exothermic in the Sb(III)-Fe(II) system.

Key words: Sb(III); ion exchange; copper refining; thermodynamics; kinetics; Purolite adsorbent

1 Introduction

Cast plates of anodic copper contain antimony that is released and gets accumulated in the copper refining electrolyte contaminating cathodic  copper [1]. This also hampers production since Sb(III) at concentrations above 50 mg/L will precipitate on the cathode plates, and also forms floating sludge that interferes with the electrolysis process and causes cathode embrittlement [2,3]. Antimony in copper-containing electrolytes used for Cu refining is mainly in Sb(III) form with some small amount as Sb(V) [4] and needs to be collected by a variety of techniques including active carbon, mineral oxides, biological substances and ion- exchange resins [5]. Although nanomaterials have been recently investigated for removal of various ions [6-12], and have shown high kinetic performance due to a significantly higher surface area to volume ratio and thus greater adsorption capacity, their potential for large-scale use is unproven due to problems which apart from the factor of cost-effectiveness include problems of stability of such materials and also the disposal of the final waste products [13,14]. The ion-exchange technique has advantages such as low cost and ease of use; however, its industrial use depends on a high enough adsorption efficiency. Generally, the pH of aqueous solutions may become a major factor in the adsorption of metal ions if it affects the structural properties of adsorbents and anolytes. This has been shown to different degrees for Cu, Pd and Ce sorption, solvent extraction and hydrometallurgical processes where a change in pH values affects ion sorption efficiency [11-16]. Stirring is a much less important parameter which is not considered critical in cation adsorption with the maximum adsorption happening under the medium stirring rates around 150 r/min [17]. The Sb(III) adsorption mechanism involves competition for adsorbent sites in which copper despite its considerable concentration difference over other electrolyte ions does not participate in, rather, the real competition is from Fe(II) which is also present in substantial amounts.

Adsorptive resins for antimony may be chosen from the amino-methyl phosphonic family commonly known as amino-phosphonic having an R—CH₂NHCH₂PO₃H₂ structure where R, could be a phenolic or divinylbenzene (DVB) polystyrene group. Purolite S597 resin used in this research is a general-purpose commercial absorbent of the phosphonate-mono phosphonic family (R—CH₂—H₂PO₃) containing phosphoric and sulfonic acid. The hydrophilic sulfonic acid group together with the hydrophobic monophosphonic acid group forms a dual sorption mechanism, where the former enhances the sorption kinetics, while the latter allows the ion-specific selectivity [18]. Figure 1 shows the chemical structure of sulfonated monophosphonic resin [19]. To the best of the authors’ knowledge, there has been no theoretical investigation of selective ion exchange sorption phenomena of antimony and competitive adsorption of Sb(III) and Fe(II) ions from Sb and Fe ion bearing solutions and their effect on copper refining process.

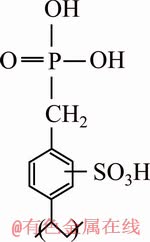
Fig. 1 Chemical structure of sulfonated monophosphonic resin [19]

Since the concomitant presence of metal ions can lead to synergism, antagonism or non-interaction, the understanding of the nature of the interactions between these triple ions is essential. Therefore, studying this system’s thermodynamics, kinetics and isotherm characteristics to find the degree of selectivity and also the adsorption sequence taking into account the interactive effect of one metal ion on the overall rate of sorption of the other is of practical and theoretical importance [20,21].

2 Experimental

Chemical and physical characteristics of Purolite S957 ion exchange resin, a chelating compound consisting of the macroporous polystyrene cross-linked divinyl benzene network with sulfonic and phosphonic acid functional groups are given in Table 1.

Atomic absorption spectroscopy (AAS) analysis results of industrial copper refinery electrolytes for Sb and Fe concentrations are given in Table 2 and were used as the basis for the formulation of antimony sulfate and iron sulfate solutions made using Merck analytical grade compounds as shown in Table 3.

Table 1 Chemical and physical characteristics of Purolite S957 ion exchange resin (Purolite International Ltd.)

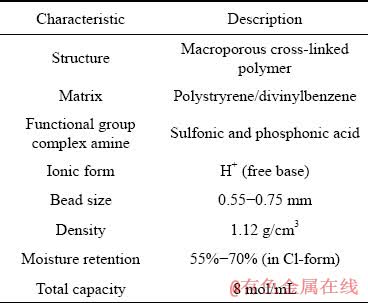
Table 2 AAS analysis results of copper refinery electrolyte (g/L)

To become fully hydrated, the fresh resin was soaked in double-distilled water for 15 min before each experiment and then 200 mL solution containing the antimony sulfate at a specified pH in quantities shown in Table 3 was added. The solution was stirred at 150 r/min during the experiment and then drained through blue band filter paper, to be analyzed for iron and antimony concentrations using Varian double-beam flame atomic absorption spectrophotometer (Varian AA-975, AA-1275). Optimal performance range of each process parameter for attaining the maximum value of removal as desirable optimized point, was determined by repeated experiments (at least three times), which were carried out at different levels of contact time (0.5, 1, 1.5, 2 and 2.5 h), pH (2, 4, 6, 8 and 10), temperature (25, 35, 45, 55 and 65 °C), and mass of resin (0.5, 2, 3.5, 5 and 6.5 g). The amount of Sb(III) adsorbed (q_e) and its removal efficiency (η) was calculated after each experiment using the following equations [22]:

q_e=V(C₀-C_e)/m                          (1)

η=[(C₀-C_e)/C₀]×100%                    (2)

where V is the volume of the solutions (mL), m is the mass of adsorbent (g), C₀ and C_e denote the initial and equilibrium concentrations (mg/L) of Sb(III), respectively.

Table 4 shows the results of experiments run on optimized variables for maximum removal exhibiting good agreement with predicted values with a relative error around 1%, suggesting that the model has high enough adequacy to predict removal percentage for this system.

3 Results and discussion

3.1 Adsorption isotherm models

The mathematical relationship between the  amount of a substance adsorbed on a surface and its concentration in the equilibrium solution at constant temperature is called the adsorption isotherm [23]. There is an important association both from theoretical and practical points of view since the parameters taken from models provide information on the mechanisms and surface properties of the sorbent [24,25]. Equilibrium data obtained from ion adsorption in different systems were analyzed through the most frequently applied isotherm models available, namely, Henry, Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich (D-R) shown in Eqs. (3)-(9), respectively. The adsorption equilibrium at a constant temperature on a homogeneous surface at low concentrations, according to Henry’s law, is a straight line when equilibrium adsorbate amount n₁ is plotted versus concentration C and Henery constant K_H (L/g):

n₁=K_HC                                (3)

where K_H is Henry constant.

Table 3 Characteristics of metallic salts to make synthetic solution samples

Table 4 Results of model verification with optimum combination

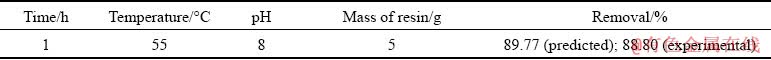
Langmuir and Freundlich isotherms are the most widely accepted surface adsorption models for single-solute systems [26]. The linear form of the Langmuir isotherm is given as follows [27,28]:

C_e/q_e=1/K_L·q_max+C_e/q_max                    (4)

where q_e is the adsorbed sorbent amount (mg/g), C_e is the equilibrium metal ion concentration in solution (mg/L), K_L is the equilibrium adsorption energy constant (L/mg), and q_max is the maximum adsorption capacity (mg/g). A linear plot is obtained when drawing C_e/q_e against C_e over the entire concentration range of investigated ions. For cases where adsorbent surface is heterogeneous [29,30], Freundlich isotherm is applicable when multilayer physisorption occurs. The logarithmic equation of Freundlich isotherm is expressed as [31-33]:

lg q_e=lg K_F+1/nlg C_e                                   (5)

where K_F ((mg/g)·(mg/L)^1/n) and n are the Freundlich constants. Based on Eq. (5) the values  of K_F and 1/n can be determined experimentally by plotting lg q_e vs lg C_e and the shape of the adsorption isotherm can be resolved according to the values of 1/n [4,5]. In this model, it is postulated that the adsorbate can be easily adsorbed when the 1/n value is between 0.1 and 0.5 and is hindered when it is greater than 2.0 [34]. Unlike the Langmuir isotherm which postulates the heat of adsorption to be independent of surface coverage [35], the Temkin model assumes it to be proportional to the number of atoms or molecules forming the absorbed layer. It is formulated as follows:

q_e=B_Tln K_T+B_Tln C_e                           (6)

where B_T=RT/b, R is the mole gas constant (8.314 J/(mol·K)), T is the thermodynamic temperate, b is a parameter related to temperature, J/mol; K_T (L/mg) is the Temkin constant. Plotting q_e vs ln C_e results in a line whose parameters would define the isotherms constants.

The D-R isotherm was also theorized to distinguish physical and chemical adsorptions of Sb(III) on a sorbent surface, using the logarithmic form of the D–R equation written as [36]:

ln q_e=ln q_s+K_adε²                             (7)

where K_ad is the D-R isotherm constant (mol²/kJ²); q_s is the theoretical isotherm saturation capacity, ε is the Polanyi potential, which is calculated as  follows [37]:

ε=RTln(1+1/C_e)                          (8)

The experimental isotherm data of the D-R equation were obtained by the linear regression method from the plot of ln q_e versus ε².

The value of mean adsorption energy, E (kJ/mol), is the free energy change when 1 mol of ion is transferred to the surface of the sorbents from the solution and it is calculated from D–R parameter K_ad as follows [38,39]:

E=-(2K_ad)^-1/2                            (9)

Interacting forces between the adsorbate and sorbent determine the value of mean adsorption energy and thus its chemical or physical nature. The physical adsorption reverses with about 8 kJ/mol energy, which is far less than that required for cutting strong bonds formed in chemical adsorption. Multi-component adsorption systems, due to the interaction and competition between different species for adsorbent sites, are complicated and various mathematical models are developed to define the effect of different ions on the adsorption process. The main models used are listed in Table 5 [40].

Table 5 Extended models used for adsorption isotherms of multi-component systems [40]

In Table 5, q_e,i is the equilibrium amount of adsorbed component i, C_e,i is the equilibrium concentration of component i, C_e,j (j=1, 2, …, N; N is the number of the components) is the equilibrium concentration of each component, K_{L(i, j)} and K_{F(i, j)} are the Langmuir and Freundlich constants for component i and j, respectively, and q_max,i represents the maximum adsorption capacity of component i. The parameters q_max,i, n_i, K_L(i, j) and K_F(i, j) are obtained from the single ion adsorption isotherms. The other parameters (η_i,j, x_i, y_i, z_i, a_i, b_j, m_i,j) can be obtained from the curve fitting method [41] based on the quality of fitting calculated through the value of RMSE (the root of mean square errors):

RMSE=           (10)

where x_obs,i and x_model,i are observed and modeled values, respectively. The adsorption kinetics of ions was studied via fitting the experimental data to different existing models including pseudo- first-order, pseudo-second-order, Elovich, and intraparticle diffusion. The linear equation for the pseudo-first-order model is expressed as

ln(q_e-q_t)=ln q_e-K₁t                       (11)

where q_e and q_t are the adsorption capacities (mg/g) at equilibrium and time t, respectively, K₁ is the rate constant (min^-1). The pseudo-second order is represented as

t/q_t=t/q_e+1/K₂q²_e                         (12)

where K₂ is the rate constant (mg/(g·h)).

The Elovich equation describes the kinetics of chemisorption by a solid from an aqueous medium [42]. The linear form of the Elovich equation is formulated as

q_t=1/βln(αβ)+1/βln t                      (13)

where α is the initial adsorption rate (mg/(g·min)), and β is related to the extent of surface coverage and activation energy for chemisorption (g/mg).

The intraparticle diffusion model involves a diffusion mechanism for the adsorption on porous materials controlled in part by the intraparticle diffusion rate of the adsorbate [43] and is expressed as

q_t=K_pt^1/2+C₁                                                   (14)

where K_p is the intraparticle diffusion rate constant (mg/(g·h^1/2)), C₁ is related to exterior to inner diffusion phenomenon, shown as the intercept of the first stage of adsorption plot and gives an idea about the thickness of the boundary layer, thus, the higher the intercept, the thicker the boundary  layer [43]. If the plot of q_t vs t^1/2 gives a straight line, then adsorption process is controlled by intraparticle diffusion only. The standard enthalpy change is estimated by applying the Van’t Hoff equation and equilibrium constant [37].

3.2 Effect of different variables on adsorption capacity

The effects of contact time, pH, temperature and mass of resin on the adsorption rate of resin are shown in Fig. 2.

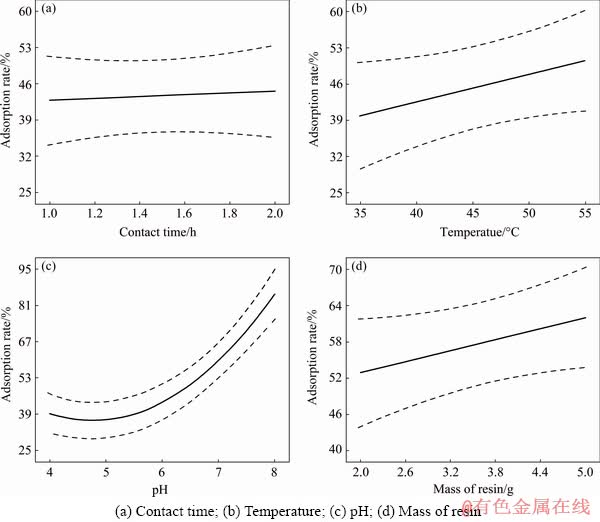
Fig. 2 Effects of various factors on adsorption of 200 mL solution containing Sb at stirring speed of 150 r/min

As it is expected, increasing contact time raises metal uptake to a level above which it stays constant (Fig. 2(a)). In the present set-up, Sb(III) reaches this point within 1 h as a large number of resin’s adsorption sites initially accommodate a high ion mass transfer towards the Purolite surface driving fast adsorption [44]. As these surface sites saturate, a quasi-equilibrium is reached and time becomes less effectual on adsorption rate as it is the inward diffusion rate that controls further adsorption. Figure 2(b) shows an increased rate of Sb(III) adsorption with temperature, indicating its endothermic nature [45]. The pH, as Fig. 2(c) demonstrates, has a pronounced effect on the adsorbing process [46] since at lower pH levels H⁺ will compete with Sb(III), thus the dominant adsorbed ion is H⁺. Purolite S957 is a weakly cationic resin having H⁺ ions in its structure that can perform well within pH range of 5-8 [47]. The mass of resin also affects adsorption to a less degree (Fig. 2(d)) as adding more adsorbent means more active sites available for taking up metal ions.

3.3 Adsorption isotherms for single-component systems

Equilibrium data for single-component electrolytes were analyzed separately by fitting data to Henry, Langmuir, Freundlich, Temkin, and Dubinin- Radushkevich isotherm equations and the results are shown in Figs. 3 and 4. The values of parameters related to each model are summarized in Table 6.

As shown in Table 6, and Figs. 3(a) and 4(a), the R₁² values for Sb(III) and Fe(II) adsorption of Henry model are 0.982 and 0.9922, respectively, indicating relative agreement of the data with this isotherm; however, when results of a plot of C_e/q_e versus C_e for the Langmuir model in Figs. 3(b) and 4(b) and Table 6 are studied although the maximum adsorption capacity for Sb(III) (38.46 mg/g) is roughly equal to that of iron (36.00 mg/g), the K_L constant for Sb(III) (0.073) is more than 27 times that of Fe(II) (0.00284), indicating the clear preference of Purolite for adsorbing Sb(III). The comparison between the coefficient of determination values for various isotherm plots indicates that the Freundlich model with R₁²=0.999 has the highest conformity. Plots of lg q_e versus lg C_e for Freundlich model for Sb(III) and Fe(II) are shown in Figs. 3(c) and 4(c). The values of K_F, 3.2 and 1.06 (mg/g)·(mg/L)^1/n, for Sb(III) and Fe(II), together with n-values of 1.83 and 1.60 for them respectively calculated from the slope and the intercept of the linear plot and listed in Table 6, show that resin has a much higher propensity for Sb(III) adsorption. The plots of q_e versus ln C_e for the Temkin model shown in Figs. 3(d) and 4(d) give

 values as low as 0.8871 for Sb(III) and 0.8892 for Fe(II) adsorption, which indicates low compatibility of the model. Dubinin–Radushkevich (D-R) isotherm is more general than the Langmuir isotherm because it does not assume a homogeneous surface or constant adsorption capacity [4]. The plots of ln q_e versus ε² shown in Figs. 3(e) and 4(e), and the values of q_s and K_ad determined from the intercept and slope of the linear plot of the data for Sb(III) (q_s=42.80 mg/g, K_ad=-2×10^-8 mol²/kJ²) and Fe(II) (q_s=25.04 mg/g, K_ad=-1×10^-7 mol²/kJ²) are given in Table 6. Also the values of E, for adsorption of Sb(III) and Fe(II), are tabulated as 5.00 and 2.27 kJ/mol, respectively, indicating physical adsorption. Therefore, in the process of absorbing Sb(III) on Purolite resin, the Freundlich model can be applied to describing adsorption, while for Fe(II), the Freundlich and Henry models describe the mechanism with the highest agreement.

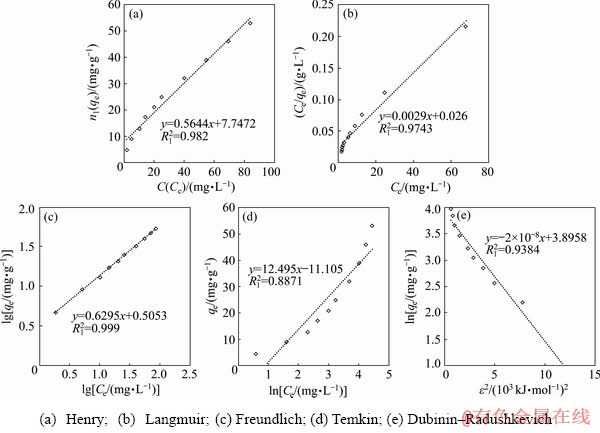
Fig. 3 Adsorption of Sb(III) ions by resin according to various isotherm models

Fig. 4 Adsorption of Fe(II) ions by resin according to various isotherm models

Table 6 Stationary isotherm models for adsorption of Sb and Fe ions on Purolite resin from single-component system (R₁ is fitting coefficient)

3.4 Adsorption isotherms for multi-component systems (Sb(III)-Fe(II))

The constants introduced for these models are calculated after fitting the adsorption data on the Purolite resin and are presented in Table 7. Based on the data, the evaluated parameters (R₁², RMSE) for Sb(III) and Fe(II) indicate that the extended Freundlich model has the highest coefficient of determination and the lowest error when describing the adsorption data on Purolite resin.

3.5 Kinetic models for single- and double-component systems

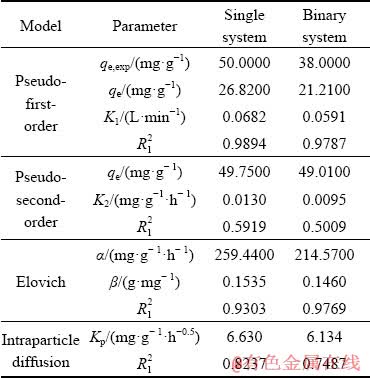
Diffusion of Sb(III) from the bulk of solution into the resin sites involves three main stages, each of which may be considered as a rate-limiting step, therefore, to determine the adsorption rate the mechanism of the reaction must be understood. The three steps include diffusion of the ions from the solution bulk to the layer surrounding the adsorbent, diffusion from this outer layer to the adsorbent surface and finally, diffusion from the surface to the internal sites [25]. The adsorption kinetics of Sb(III) and Fe(II) onto the resin was evaluated by pseudo-first-order, pseudo-second-order, Elovich, and intraparticle diffusion models. The conformity between experimental data and the model-predicted values was expressed by the correlation coefficients. From the experimental results q_e,ex and the adsorption capacity in the calculated equilibrium state q_e,cal, the R₁² adsorption parameter of the pseudo-second-order model obtained from Eq. (12) (Figs. 5(b), 6(b) and Table 8) is low for both single (0.5919) and two-component (0.5009) systems, therefore, this kinetic model is not suitable. According to the analysis of experimental data (Figs. 5(c), 6(c) and Table 8), using the Elovich equation based on Eq. (13), the R₁² value is 0.9303 for single system and 0.9769 for the binary system), therefore, the Elovich model is  not suitable for this system. The complication  arises from that, in a one-component system, Sb(III) easily cross the surrounding layer around the adsorbent to reach the internal sites (Fig. 5(d)). However, when Fe(II) is also present as a second component in the solution, a competition takes place between the ions. In the intraparticle diffusion model, the permeation rate of Sb(III) in the absorbent is mainly due to the resin structure, which has a small pore size of less than 40 nm in comparison with the large size of the Sb(III), preventing them to penetrate deeply into the resin’s active sites. The curve of capacity versus time for intraparticle diffusion model (Fig. 6(d)) shows only two-stages of the adsorption process and the diffusion step from the surface into the resin almost disappears. This is due to further space limitation by competing ions versus Sb(III) and blocking its ion [48]. The comparison of constant K₂ in the intraparticle diffusion model obtained from both systems shows that Fe(II) in the two-component system limits the available surface sites and absorption capacity of the resin for antimony (Table 8). Therefore, this model cannot describe the rate-determining step due to its high external resistance to the mass transfer on the surface of particles. The comparison of the results from the pseudo-first-order, pseudo-second-order, and intraparticle diffusion models shows that the R₁² value of the pseudo-first-order kinetic model based on Eq. (11) as plotted in Figs. 5(a) and 6(a), has the best-fit values (0.9894 for single system and 0.9787 for binary system), corroborating the physical nature of Sb(III) adsorption in both systems.

Table 7 Multi-component isotherm parameters for Sb(II) and Fe(II) adsorption on Purolite S957

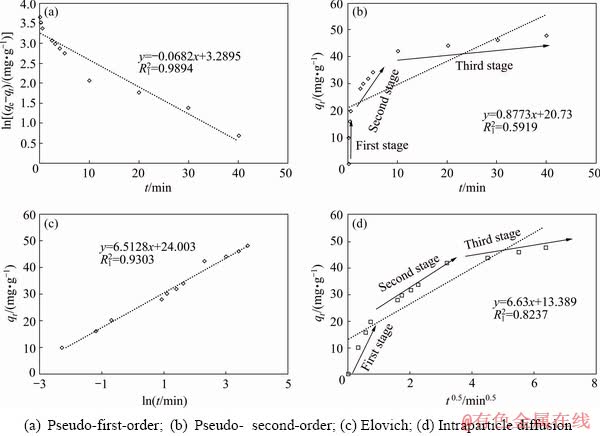
Fig. 5 Adsorption kinetic curves according to various models in single system

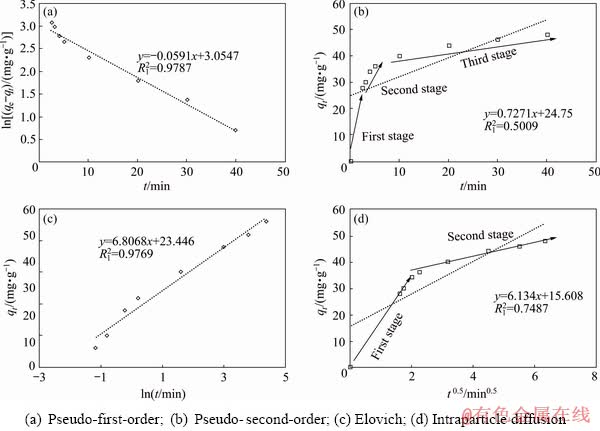
Fig. 6 Adsorption kinetic curves according to various models in binary system

Table 8 Kinetic parameters of adsorption of Sb ions by Purolite resin in single and binary systems

3.6 Thermodynamic parameters

Figure 7 shows the results of fitting the Vant’s Hoff equation to equilibrium Sb(III) adsorption data in single system (Fig. 7(a)) and binary system  (Fig. 7(b)). The values of the thermodynamic parameters (△G^Θ, △H^Θ, and △S^Θ) are summarized in Table 9.

According to Table 9, negative △G^Θ values indicate that Sb(III) adsorption is spontaneous in both systems and the small positive enthalpies for Sb(III) or Fe(II) signify the physical and endothermic nature of adsorption. In conclusion, the bond formed between the metal ions and the active resin sites is of secondary type and metal ion is weakly attached to resin surface; however, when both Fe(II) and Sb(III) are present and compete for resin’s limited surface sites, indicating that the adsorbed iron ions will be part of the energy balance of the system whereby, Fe(II) desorption takes place to accommodate the Sb(III). This alters the nature of reaction to an exothermic one, thus, as the temperature rises, △G^Θ becomes more negative, indicating increased spontaneity [49]. Table 9 shows different entropy change (△S^Θ) values for the two systems, indicating the associative/dissociative nature of the adsorption process. A △S^Θ greater than -10 J/(mol·K), is indicative of a dissociative mechanism [50] which in the present context, could confirm the dissociative mechanism of exchange of resin and electrolyte’s cations raising the entropy [51]. The release of water molecules generated during the ion exchange reaction also contributes to this increase. The positive entropy value measured for adsorption from single type ion solutions is the result of increase in entropy at the solid-liquid interface during the process, while in the binary system, the level of disorder diminishes since the overall exchange with surface sites decreases due to the competition between ions and consequently, their diminished access to free surface sites. Within a short time after the introduction of electrolytes, the internal surface of the resin becomes inaccessible because of the accumulation of ions in a layer next to the surface causing a reduction of the resin capacity for Sb. This, however, will change if the contact time is unrealistically increased.

3.7 Elution

The elution procedure was performed on the resin to establish the degree of recovery as well as the end life of the polymer. The experiments were carried out using 500 mL chloric acid at different concentrations, temperatures, and flow velocities. Resin load is estimated to be 0.35 g/L and sampling from effluent for each separate experiment was made at a constant 25 BV (bed volume, 1 BV equals 25 mL) (125 mL). The results are shown in Table 10 and Fig. 8.

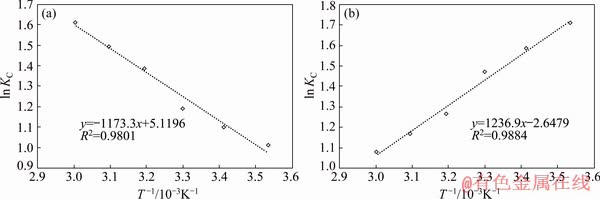
Fig. 7 Plots of Van’s Hoff equation for single (a) and binary (b) systems in optimum conditions

Table 9 Thermodynamic parameters of adsorption of Sb(III) by Purolite resin from single and binary systems

Table 10 Optimum conditions for elution of pregnant resin

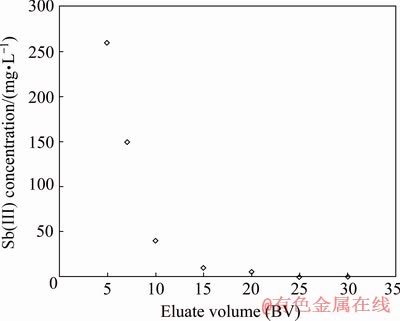
Fig. 8 Elution diagram for Sb(III) from Purolite S957 resin under optimum conditions with original resin load of 0.35 g/L

Figure 8 shows that the complete recovery of Sb(III) from Purolite resin happens at 25 BV from elution liquid resulting in Sb(III) concentration of 250 mg/L.

The experiments showed that a higher concentration of HCl results in enhanced elution with complex chlorine-based anions. Overall, the flow rate has a pronounced effect on elution outcome with lower flow rates, and longer staying time shows a greater elution efficiency. A new experiment started with fresh resin and after 6 regenerations the resin was still in good condition.

4 Conclusions

(1) The controlled removal of Sb(III) through ion exchange is possible within an optimal range for independent variables of time, temperature, pH, and mass of resin with a maximum efficiency of 90% for the copper extraction process. The pH was shown to have an eminent effect with the highest outcomes obtained at the pH values around 8.

(2) The Freundlich isotherm showed the highest compatibility for single ion solution and extended Freundlich for the two components.

(3) The pseudo-first-order model can be used as the model for the kinetics of adsorption.

(4) The negative Gibbs free energy values indicate the spontaneous Sb adsorption in either single or binary systems. The small positive value of enthalpy for single ion adsorption shows an endothermic process, but when Fe is also present it counters adsorption of Sb ions on the resin sites. Therefore, an ion dislodgement process with opposite energy expenditure occurs and as a result, the process becomes somewhat exothermic.

Acknowledgments

The authors acknowledge the Sarcheshmeh Copper Complex-Iran, for financial support and also in allowing them to use the refinery solutions.

References

[1] NAVARRO P, ALGUACIL F J. Adsorption of antimony and arsenic from a copper electrorefining solution onto activated carbon [J]. Hydrometallurgy, 2002, 66: 101-105.

[2] DAVIS J R. Copper and copper alloys [M]. New York: ASM International, 2001: 3-9.

[3] SCHLESINGER M, PAUNOVIC M. Modern electroplating [M]. 5th ed. New York: Wiley, 2011: 1-6.

[4] SALARI K, HASHEMIAN S, BAEI M T. Sb(V) removal from copper electrorefining electrolyte: Comparative study by different sorbents [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 440-449.

[5] FAN H T, SUN W, JIANG B, WANG Q J, LI D W, HUANG C C, WANG K J, ZHANG Z G, LI W X. Adsorption of antimony(III) from aqueous solution by mercapto- functionalized silica-supported organic-inorganic hybrid sorbent: Mechanism insights [J]. Chemical Engineering Journal, 2016, 286: 128-138.

[6] RABIUL AWUAL M D, YAITA T, TAGUCHI T, SHIWAKU H, SUZUKI S, OKAMOTO Y. Selective cesium removal from radioactive liquid waste by crown ether immobilized new class conjugate adsorbent [J]. Journal of Hazardous Materials, 2014, 278: 227-235.

[7] RABIUL AWUAL M D, MIYAZAKI Y, TAGUCHI T, SHIWAKU H, YAITA T. Encapsulation of cesium from contaminated water with a highly selective facial organic- inorganic mesoporous hybrid adsorbent [J]. Chemical Engineering Journal, 2016, 291: 128-137.

[8] RABIUL AWUAL M D, ALHARTHI N H, HASAN MANJUR M D, KARIM M R, ISLAM A, ZNAD H, HOSSAIN M A, HALIM ERSHAD M D, RAHMAN M M, KHALEQUE ABDUL M D. Inorganic-organic based novel nano-conjugate material for effective cobalt(II) ions capturing from wastewater [J]. Chemical Engineering Journal, 2017, 324: 130-139.

[9] RABIUL AWUAL M D, ALHARTHI H N, HASAN MANJUR M D, KARIM REZAUL M, ISLAM A, ZNAD H, HOSSAIN M A, HALIM ERSAHD M D, RAHMAN M M, KHALEQUE ABDUL M D. Ligand field effect for dysprosium(III) and lutetium(III) adsorption and EXAFS coordination with novel composite nanomaterials [J]. Chemical Engineering Journal, 2017, 320: 427-435.

[10] RABIUL AWUAL M D, HASAN MANJUR M D, KHALEQUE ABDUL M D, SHEIKH CHANMIYA M D. Treatment of copper(II) containing wastewater by a newly developed ligand-based facial conjugate materials [J]. Chemical Engineering Journal, 2016, 288: 368-376.

[11] RABIUL AWUAL M D, RAHMAN I M M, YAITA T, KHALEQUE ABDUL M D, FERDOWS M. pH-dependent Cu(II) and Pd(II) ions detection and removal from aqueous media by an efficient mesoporous adsorbent [J]. Chemical Engineering Journal, 2014, 236: 100-109.

[12] RABIUL AWUAL M D, HASAN MANJUR M D, SHAHAT A, NAUSHAD U, SHIWAKU H, YAITA T. Investigation of ligand immobilized nano-composite adsorbent for efficient cerium(III) detection and recovery [J]. Chemical Engineering Journal, 2015, 265: 210-218.

[13] RABIUL AWUAL M D, ISMAEL M, YAITA T, EL SAFTY S A, SHIWAKU H, OKAMOTO Y, SUZUKI S. Trace copper(II) ions detection and removal from water using novel ligand modified composite adsorbent [J]. Chemical Engineering Journal, 2013, 222: 67-76.

[14] RABIUL AWUAL M D. Ring size-dependent crown ether-based mesoporous adsorbent for high cesium adsorption from wastewater [J]. Chemical Engineering Journal, 2016, 303: 539-546.

[15] RABIUL AWUAL M D, SUZUKI S, TAGUCHI T, SHIWAKU H, OKAMOTO Y, YAITA T. Radioactive cesium removal from nuclear wastewater by novel inorganic and conjugate adsorbents [J]. Chemical Engineering Journal, 2014, 242: 127-135.

[16] RABIUL AWUAL M D, YAITA T, EL SAFTY S A, SHIWAKU H, SUZUKI S, OKAMOTO Y. Copper(II) ions capturing from water using ligand modified a new type of mesoporous adsorbent [J]. Chemical Engineering Journal, 2013, 221: 322-330.

[17] GARG U K, KAUR M P, GARG V K, SUD D. Removal of nickel(II) from aqueous solution by adsorption on agricultural waste biomass using a response surface methodological approach [J]. Bioresource Technology, 2008, 99: 1325-1331.

[18] CHIARIZA R, HORWITZ E P, ALEXANDRATORS S D. Diphonix resin: A review of its properties and applications [J]. Separation Science and Technology, 1997, 32: 1-35.

[19] AREXANDRATOR S, SHELLEY C A, HORWITZ E P, CHIARIZIA R. Bi-functional phenyl monophosphonic sulfonic acid ion exchange resin and process for using the same method: USA patent, US 6488859 B2 [P]. 2003-03-12.

[20] NEBEKER N, HISKEY J B. Recovery of rhenium from the copper leach solution by ion exchange [J]. Hydrometallurgy, 2012, 125-126: 64-68.

[21] CHEN Y, HE Y, YE W, JIA L. Competitive adsorption characteristics of Na(I)/Cr(III) and Cu(II)/Cr(III) on GMZ bentonite in their binary solution [J]. Journal of Industrial and Engineering Chemistry, 2014, 26: 335-339.

[22] GILSA E, MAICANEANU A, GHIRISAN A, ILEA P. Kinetic modeling and error analysis for zinc removal on a weak base anion exchange resin [J]. Desalination and Water Treatment, 2015, 57: 1-9.

[23] NAFFRECHOUX E, HAMDAOUI O. Modeling of adsorption isotherms of phenol and chlorophenols onto granular activated carbon: Part II. Models with more than two parameters [J]. Journal of Hazardous Materials, 2007, 147: 381-394.

[24] SRIVASTAVA V C, MALL I D, MISHRA I M. Equilibrium modeling of single and binary adsorption of cadmium and nickel onto bagasse fly ash [J]. Chemical Engineering Journal, 2006, 117: 79-91.

[25] DESTA M B. Batch sorption experiments: Langmuir and freundlich isotherm studies for the adsorption of textile metal ions onto teff straw (Eragrostis tef) agricultural waste [J]. Journal of Thermodynamics, 2013(1): 1-6. Article ID 375830.

[26] OKEOLA F, ODEBUNMI E. Freundlich and Langmuir isotherms parameters for adsorption of methylene blue by activated carbon derived from agro wastes [J]. Advances in Natural and Applied Sciences, 2010, 4: 281-289.

[27] del BUBBAA M, ARIASB CA, BRIX H. Phosphorus adsorption maximum of sands for use as media in subsurface flow constructed reed beds as measured by the Langmuir isotherm [J]. Water Research, 2003, 37: 3390-3400.

[28] LEWINSKY A A. Hazardous materials and wastewater treatment, removal and analysis [M]. New York: Nova Science Publishers, 2007: 5-10.

[29] XIONG C, YAO C. Adsorption behavior of MWAR toward Gd(III) in aqueous solution [J]. Iranian Journal of Chemistry and Chemical Engineering (IJCCE), 2010, 29: 59-66.

[30] NUR T, NGUYEN T C, VIGNESWARAN S, SINGH G, KANDASAMY J. Batch, and column adsorption and desorption of fluoride using hydrous ferric oxide: Solution chemistry and modeling [J]. Chemical Engineering Journal, 2014, 247: 93-102.

[31] COONEY D O. Adsorption design for wastewater treatment [M]. New York: Taylor & Francis, 1998.

[32] DADA A O, OLATUNYA A P. Langmuir, freundlich, temkin and dubinin-radushkevich, isotherms studies of equilibrium sorption of Zn²⁺ unto phosphoric acid modified rice husk [J]. IOSR Journal of Applied Chemistry, 2012, 3: 38-45.

[33] SPARKS D L. Environmental soil chemistry [M]. New York: Academic Press, 1995.

[34] LI D, LI J, GU Q, SONG S, PENG C. Co-influence of the pore size of adsorbents and the structure of adsorbates on adsorption of dyes [J]. Desalination and Water Treatment, 2016, 57: 14686-14695.

[35] INYINBOR A A, ADEKOLA F A, OLATUNJIO G A. Kinetics, isotherms and thermodynamic modeling of liquid-phase adsorption of Rhodamine B dye onto Raphia hookerie fruit epicarp [J]. Water Resources and Industry, 2016, 15: 14-27.

[36] NGUYEN C, DO D D. The Dubinin–Radushkevich equation and the underlying microscopic adsorption description [J]. Carbon, 2001, 39: 1327-1336.

[37] DHOBLE R M, LUNGE S, BHOLE A G, RAYALU S. Magnetic binary oxide particles (MBOP): A promising adsorbent for removal of As(III) in water [J]. Water Research, 2011, 45: 4769-4781.

[38] CHEN S G, YANG R T. Theoretical basis for the potential theory adsorption isotherms: The Dubinin-Radushkevich and Dubinin-Astakhov equations [J]. Langmuir, 1994, 10: 4244-4249.

[39] FAN H T, SHI L Q, SHEN X, XIE K P. Equilibrium, isotherm, kinetic and thermodynamic studies for removal of tetracycline antibiotics by adsorption onto hazelnut shell derived activated carbons from aqueous media [J]. RSC Advances, 2016, 6: 109983-109991.

[40] FOULADGAR M, BEHESHTI M, SABZYAN H. Single and binary adsorption of nickel and copper from aqueous solutions by γ-alumina nanoparticles: Equilibrium and kinetic modeling [J]. Journal of Molecular Liquids, 2015, 211: 1060-1073.

[41] FATHI M B, REZAII B, ALAMDARI E K. Competitive adsorption characteristics of rhenium in single and binary (Re-Mo) systems using Purolite A170 [J]. International Journal of Mineral Processing, 2017, 169: 1-6.

[42] LEE I H, KUAN Y C, CHERN J M. Equilibrium and kinetics of heavy metal ion exchange [J]. Journal of the Chinese Institute of Chemical Engineers, 2007, 38: 71-84.

[43] BONILLA P A, MENDOZA-CASTILLO D I, REYNEL H E. Adsorption processes for water treatment and purification [M]. Heidelberg: Springer, 2017.

[44] SHUANIDAN L, LE T, JU S, JIN H P, LI B Z. Removal of methylene blue from aqueous solutions using a novel granular red mud mixed with cement in light metals [M]. Heidelberg: Springer, 2016: 131-136.

[45] MUFAZZAL S M, AHMED M. Effect of temperature on kinetics and adsorption profile of endothermic chemisorption process: Tm(III)–pan loaded system [J]. Separation Science and Technology, 2006, 41: 705-722.

[46] WANG Q, LUAN Z, WEI N, LI J, LIU C. The color removal of dye wastewater by magnesium chloride/red mud (MRM) from aqueous solution [J]. Journal of Hazardous Materials, 2009, 170: 690-698.

[47] XI J, HE M, LIN C. Adsorption of antimony(V) on kaolinite as a function of pH, ionic strength and humic acid [J]. Environmental Earth Sciences, 2010, 60: 715-722.

[48] ZHANG Y, JIANG J, MAOZHE C. Minteq modeling for evaluating the leaching behavior of heavy metals in MSWI fly ash [J]. Journal of Environmental Sciences, 2008, 20: 1398-1402.

[49] XIONG C. Sorption behavior of D155 resin for Ce(III) [J]. Indian Journal of Chemistry A, 2008, 47: 1377-1380.

[50] KHAN M D A, AKHTAR A, NABI S A. Kinetics and thermodynamics of alkaline earth and heavy metal ion exchange under particle diffusion-controlled phenomenon using polyaniline- Sn(IV) iodophosphate nanocomposite [J]. Journal of Chemical & Engineering Data, 2014, 59: 2677-2685.

[51] XIONG Y, XU J, SHAN W, LOU Z, FANG D, ZANG S, HAN G. A new approach for rhenium (VII) recovery by using modified brown algae Laminaria Japonica adsorbent [J]. Bioresource Technology, 2013, 127: 464-472.

单离子体系和Sb(III)-Fe(II)二元体系中Sb(III)在阳离子交换树脂上的吸附行为：吸附平衡、动力学和热力学

F. MOGHIMI¹, A. H. JAFARI², H. YOOZBASHIZADEH³, M. ASKARI³

1. Department of Materials Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran;

2. Department of Materials Science and Engineering, College of Engineering, Shahid Bahonar University of Kerman, Kerman, Iran;

3. Department of Materials Science and Engineering, Sharif University of Technology, Tehran, Iran

摘  要：研究含铜水溶液中Sb(III)和Fe(II)离子在Purolite S957(一种可商购的阳离子交换吸附剂)上的竞争吸附机理。使用含有单离子或多离子的硫酸铜水溶液，采用固定吸附和间歇吸附技术，研究吸附过程对pH、树脂质量、接触时间和温度变化的敏感性，确定获得最大离子去除率的最佳参数范围。利用非线性回归技术，将单离子吸附实验数据用Henry、Langmuir、Freundlich、Temkin和Dubinin-Radushkevich等温线模型进行拟合。Sb(III)的Freundlich等温线以及Fe(II)溶液的Freundlich和Henry等温线对吸附平衡数据的拟合最好；而对于二元离子电解质，扩展的Freundlich模型对实验数据的拟合令人满意。描述吸附过程的动力学模型为准一级模型，说明物理吸附在吸附过程中的主导作用。吸附过程的热力学参数揭示单离子体系和含Sb(III)-Fe(II)电解质中Sb(III)吸附机理的差异。Sb(III)单独吸附为吸热过程，而Sb在Sb-Fe体系中的吸附为放热过程。

关键词：Sb(III)；离子交换；铜精炼；热力学；动力学；Purolite吸附剂

 (Edited by Wei-ping CHEN)

Corresponding author: A. H. JAFARI; Tel/Fax: +98-342817708; E-mail: Jafari.a.h@uk.ac.ir

DOI: 10.1016/S1003-6326(19)65195-2