DOI: 10.11817/j.issn.1672-7207.2015.11.040
避难硐室温度计算模型及影响因素
黄志凌1, 2,金龙哲1, 2,詹子娜1, 2,李芳玮3
(1. 北京科技大学 土木与环境工程学院,北京,100083;
2. 矿山避险技术研究中心,北京,100083;
3. 国家安全生产监督管理总局 研究中心,北京,100713)
摘要:针对避难硐室等井下密闭空间内温升问题,以热力学方程为基础,建立受围岩传热、内部产热影响下的避难硐室温度计算模型,采用Matlab迭代计算得到硐室内温度变化曲线,实验验证其合理性并对计算模型进行修正;利用修正的计算模型对巷道壁面温度、岩石导热系数、原岩温度、调温圈半径等影响因子进行正交实验分析,并对壁面温度和导热系数这2个因素的影响效果进行进一步分析。研究结果表明:各因素影响程度由大到小顺序为壁面温度、岩石导热系数、原岩温度、调温圈半径。
关健词:避难硐室;温度;数学模型;导热系数
中图分类号:X936 文献标志码:A 文章编号:1672-7207(2015)11-4274-07
Mathematical model and influencing factor of temperature in refuge chamber
HUANG Zhiling1, 2, JIN Longzhe1, 2, ZHAN Zina1, 2, LI Fangwei3
(1. School of Civil & Environment Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Mine Emergency Technology Research Center, Beijing 100083, China;
3. National Research Center, State Administration of Work Safety, Beijing 100713, China)
Abstract: A temperature calculation model of refuge chamber under the influence of rock heat transfer and internal heat was built, based on the thermodynamic equations, aimed at the increase of the temperature in the confined underground space, such as the refuge chamber. The temperature curve inside refuge chamber was generated by calculating the model with Matlab, and the model was revised according to the comparison of calculation result and experiment. On the basis of the corrected model, an orthogonal experiment was conducted to analyze the factors that influence the temperature in refuge chamber, including the temperature of the roadway surface, the rock thermal conductivity, the temperature of the original rock, and the radius of the controlled temperature circle. Further research on roadway surface temperature and thermal conductivity was conducted. The results show that the most important factor is temperature of roadway surface, and others are rock thermal conductivity, temperature of the original rock, and the radius of the controlled temperature circle.
Key words: refuge chamber; temperature; mathematical model; thermal conductivity
避难硐室作为矿井灾变情况下应急避险的密闭空间,内部气体环境的安全性及舒适性直接影响避险人员生理、心理健康[1]。在避难硐室内进行的多次载人实验均表明,外部压风中断时避险人员体感温度高、舒适性差,人员长期处在高温密闭环境下易引起中暑,严重时可能扰乱体温调节、水盐代谢、消化系统等生理功能,因而控制密闭空间温度是亟待解决的关键技术问题。避难硐室内温度的定量计算及其影响因素的研究,对建立包含选址、设计、制冷技术在内的综合温控技术,保障避险人员的生理、心理健康具有重要意义。国内外针对密闭井巷空间内温度变化规律研究的报道较少,在地铁、隧道、地下商场、人防等工程的传热问题方面有类似研究[2-13],所采用的方法主要包括理论计算、数值模拟、实验测试等,其研究方法、考虑因素、计算假定对于本文的研究具有一定的借鉴意义,但其研究的对象多为开放空间,与密闭井巷空间存在差异,同时现有研究多考虑初始围岩温度为均一值,而避难硐室围岩在调温圈半径内存在温度梯度。为此,本文作者针对避难硐室等井下密闭空间内的温升问题,建立温度计算模型,进行现场实验对模型验证和修正,并对其影响因素进行研究,从而为井下密闭空间综合温控技术的建立提供理论依据。
1 模型的建立
避难硐室内温度的影响因素主要有人体产热(Qperson)、围岩导热(Qearth)、设备运行放热(Qdevice)、硐室与外部巷道的热交换(Qwall)、制冷设备的吸热(Qrefrigeration)、供回风热交换(Qventilation)等,其热载荷物理模型如图1所示。
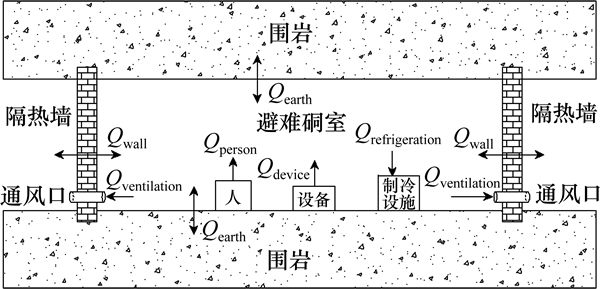
图1 避难硐室热载荷模型
Fig. 1 A model of heat load in refuge chamber
为简化模型方便计算,进行如下设定。
1) 不考虑供回风热交换的影响。灾变情况下硐室外部供风容易中断,且在压缩氧供氧的情况下硐室内亦没有压风供给。
2) 制冷措施降低空间内温度,计算过程中不考虑内部制冷设备的作用,增大安全系数。
3) 忽略硐室与外部巷道中空气的热交换。灾变后外部巷道高温持续时间较短[14],同时受隔热墙隔热、过渡区缓冲的影响,外部巷道对生存区的温度影响小。
4) 将巷道断面等效为圆形截面巷道,半径采用当量半径表征[15-16]。
以上假设虽然降低了计算结果的精度,但简化了计算过程,使得计算可行。
人体散热量是一个动态、复杂的指标,本文采用经验数据,考虑人员在避难硐室过程中主要为静坐休息的状态,取其产热功率为116 W[17-18],则避难硐室内人员产热功率P1采用下式计算。
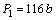 (1)
(1)
式中:b为避难人员数。
设备产热主要由包括传感器、灯、风机等在内的电器设备运行产热、CO2处理药剂放热等组成。以某厂家LiOH型二氧化碳吸收剂为例,其产热量为1.4 kJ/g,100人硐室每小时约消耗10 kg该吸收剂,则其产热量为14 000 kJ/h。硐室内载人运行过程中,电器设备功率通常不超过500 W,假定500 W功率全部用于发热,其产热量为1 800 kJ/h,而通常非制热电器设备运转时仅有少量能量用于产热,因此可认为电器设备产热远远小于药剂反应放热,不考虑其对硐室温度的影响。对CO2吸收处理是个放热反应,其产热功率可用下式计算。
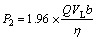 (2)
(2)
式中:Q为单位质量药剂反应产热量;VL为人均二氧化碳释放速率;η为药剂吸附效率。
将围岩划分成微元,如图2所示,将硐室空气及围岩温度的变化过程划分成时间微元,避难期间硐室内产生的热量被空气吸收,使得硐室内空气温度上升,升温的空气与第1层围岩微元发生热交换,第1层微元与第2层微元发生热交换,层层传递将热量传导至围岩中。
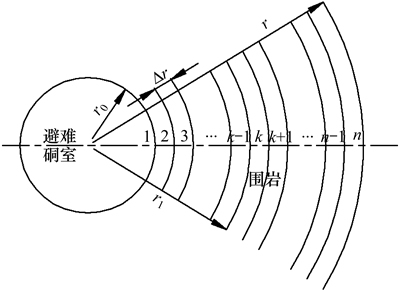
图2 围岩微元划分
Fig. 2 Infinitesimal element of surrounding rock
空气受避难期间热量的影响发生的热交换过程可用下式表示。
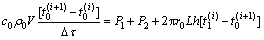 (3)
(3)
式中:c0为空气比热容;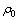 为密度;V为硐室生存区空间体积;
为密度;V为硐室生存区空间体积;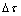 为时间微元;
为时间微元;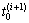 和
和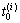 分别为第i+1和i时刻空气的温度;
分别为第i+1和i时刻空气的温度;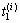 为巷道围岩第1层微元第i时刻的温度;L为硐室生存区长度;h为硐室内空气与壁面对流换热系数。
为巷道围岩第1层微元第i时刻的温度;L为硐室生存区长度;h为硐室内空气与壁面对流换热系数。
第1层微元与第2层微元的热交换过程可用下式表示:
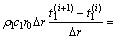
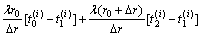 (4)
(4)
式中:c1为岩石比热容;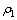 为密度;
为密度;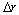 为巷道壁微元;r0为巷道当量半径;
为巷道壁微元;r0为巷道当量半径;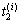 为第2层巷道围岩微元第i时刻的温度;λ为岩石导热系数。
为第2层巷道围岩微元第i时刻的温度;λ为岩石导热系数。
假定巷道围岩为各向同性的单元,且传热过程不考虑轴向的热量交换,则圆柱坐标系下导热微分方程为
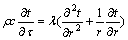
则第n层巷道微元的热交换过程为
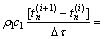
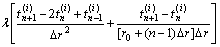 (5)
(5)
式中: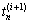 和
和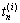 分别为第n层巷道围岩微元第i+1和第i时刻的温度。
分别为第n层巷道围岩微元第i+1和第i时刻的温度。
对式(1)~(5)进行合并化简,可得:
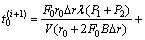
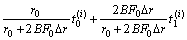 (6)
(6)
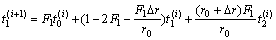 (7)
(7)
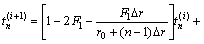
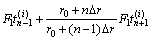 (8)
(8)
式中:F0和F1表征无因次时间,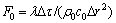 ,
,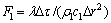 ;B表征无因次散热系数,
;B表征无因次散热系数,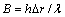 。
。
假定初始状态下,巷道围岩内的温度呈圆筒壁稳态导热分布,则有:
 (9)
(9)
式中:te为围岩原岩温度;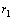 为巷道调温圈半径。
为巷道调温圈半径。
在测定围岩基本岩性的基础上,利用式(6)~(9)进行迭代计算,即可得到硐室内温度变化规律。可为煤矿、非煤矿山避难硐室的设计、温度控制提供支撑,亦可利用该模型对不同选址方案的平衡温度进行预测。
2 模型的实验验证与修正
利用所推导的温度计算模型,针对某永久避难硐室采用Matlab软件进行迭代计算,将计算结果与在该硐室进行的现场载人实验结果对比,对比曲线如图3所示。
现场实验数据与理论计算结果均表明,避难硐室内温度上升到一定值后,将保持平稳不再上升,此时空间内达到热平衡状态,产热与散热量基本保持一致。
硐室内温度在载人实验进行到420 min时达到峰值27.5 ℃,后因实验时间进入晚上,人员活动量减少导致产热降低,且围岩温度、外部巷道温度均有所降低,硐室内温度略降后在26.9 ℃左右波动。模型计算结果则在350 min时硐室内达到热平衡,温度稳定在28.2 ℃。
由图3可见:计算结果与实验结果在温度变化趋势上保持一致,但理论计算结略高于实验结果,其温差为1.3 ℃,达到温度平衡时间现场实验早70 min,其可能的原因是:
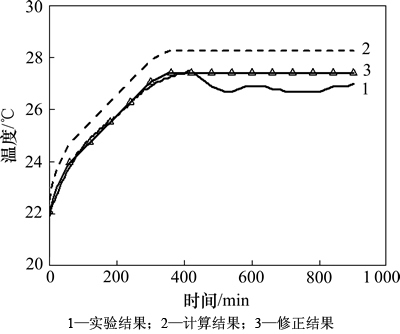
图3 理论计算、现场实验和修正结果温度曲线
Fig. 3 Temperature curves of calculation, experiment and revise results
1) 在理论计算中,将围岩假设为各向同性的物质,导致计算结果与实际有所偏离;
2) 为简化计算,忽略了岩体的轴向导热,从而导致理论计算结果与实验相比较高。
3) 实验过程中,生存区内空间并非绝对的对外隔热密闭,通过两端的密闭墙向外散失一定的热量。
根据实验结果,对模型进行修正,取修正系数k为0.97,则硐室内温度计算公式为
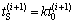 (10)
(10)
式中: 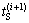 为修正后的硐室环境温度。
为修正后的硐室环境温度。
修正后的温度变化曲线如图3所示,将修正后的公式在其他避难硐室进行应用,其结果如图4所示。
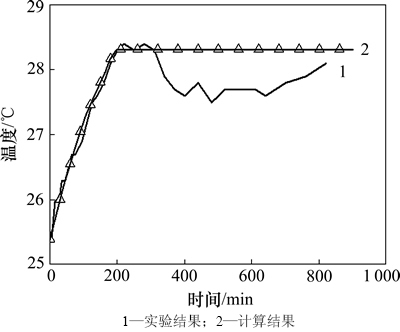
图4 修正后公式计算与实验结果对比
Fig. 4 Comparison of calculation and experiment results
由图3和图4可见:取修正系数之后,计算结果与实验结果基本相符,可知计算结果较为可靠,能够反映避难硐室内温度变化规律。
3 温度变化影响因素分析
避难硐室围岩的热力学性质直接影响硐室空间内的温度变化,本文选取巷道壁面温度、导热系数、调温圈半径和原岩温度4个因素进行分析。
考虑国内矿井井下巷道的实际情况,依据现场经验并结合相关文献,确定对壁面温度t1为20,24,28和32 ℃,岩石导热系数λ为1,2,3和4 W/(m·K),调温圈半径r1为10,20,30和40 m,原岩温度te为20,28,36和44 ℃的情况进行4因素4水平正交设计,利用所推导的温度模型进行计算,正交表及计算结果如表1所示。表中R代表由各因素引起的平均效果的极差,极差越大表示该因素对考核指标的影响越大。
表1 正交试验结果及分析
Table 1 Results of calculation with calculation model
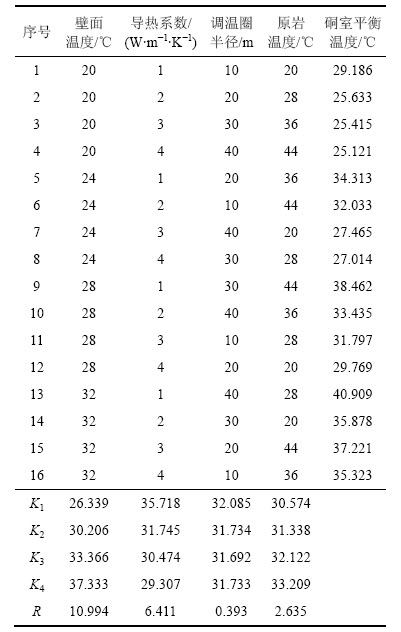
由表1可知:硐室内达到平衡的温度与壁面温度、调温圈半径、原岩温度呈正相关关系,而与导热系数
呈负相关关系。壁面温度、导热系数、调温圈半径和原岩温度的R分别为10.994,6.411,0.393和2.635。
分析认为,人员避难期间,硐室内产热对于围岩的温度影响范围有限,通常只能引起处于调温圈半径内的小范围围岩温度的变化,因此,调温圈半径、原岩温度对硐室的平衡温度影响较壁面温度、岩石导热系数的影响小。
壁面温度、岩石导热系数对硐室内的温度变化的影响效果大大高于调温圈半径、原岩温度的影响效果,针对这壁面温度、围岩导热系数的影响效果做进一步分析。
假定导热系数为1 W/(m·K),调温圈半径为20 m,原岩温度为36 ℃,对壁面温度为20,24,28和32 ℃时硐室内温度变化进行解算,结果如图5所示。
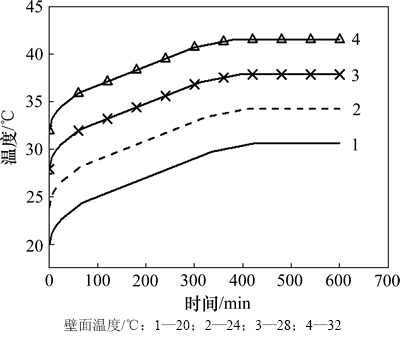
图5 不同壁面温度下硐室温升
Fig. 5 Temperatures change of refuge chamber with different wall temperatures
由图5可知:壁面温度直接影响硐室的平衡温度,但是对硐室内温度的变化速率并未发现明显的影响,同时可知壁面温度与原岩温度之间的温差越小,则硐室内温度达到平衡状态所需的时间越短。
假定壁面温度为24 ℃,调温圈半径为20 m,原岩温度为36 ℃,对导热系数为1,2,3和4 W/(m·K)时硐室内的温度变化进行解算,结果如图6所示。
由图6可知:导热系数对硐室温度的影响表现升温速率及最终平衡温度2个方面。同等条件下,导热系数越小则硐室内升温越快,且最终平衡温度越高。
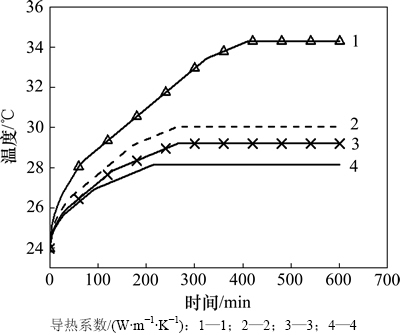
图6 不同导热系数下硐室温升
Fig. 6 Temperatures change of refuge chamber with different thermal conductivities
4 温度计算模型的工程应用
根据前面所推导的避难硐室温度数学模型及对其影响因素的分析结果,为避难硐室的工程设计提供指导。
以某矿100人永久避难硐室为例,在对采区内的工作面、人员分布、地质情况进行调查分析之后,结合避难硐室的布置原则,初步选定该避难硐室2个布置方案,如图7所示。
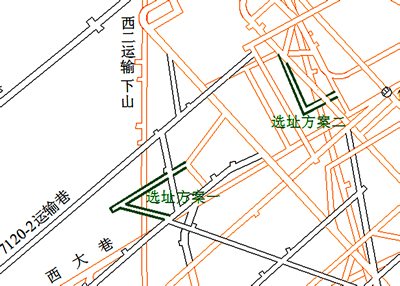
图7 避难硐室选址方案
Fig. 7 Site selection of refuge chamber
方案1中原岩温度为39.2 ℃,壁面温度为30.4 ℃,方案2中原岩温度为39.5 ℃,壁面温度为33.8 ℃,其围岩均主要为砂质泥岩。
对2种选址的避难硐室整体结构进行初步设计,确定避难硐室生存空间体积及巷道断面之后,利用温度模型进行计算,结果如图8所示。选址方案1的平衡温度为34.2 ℃,选址方案2的平衡温度为38 ℃,最终选定方案1作为该避难硐室的选址。
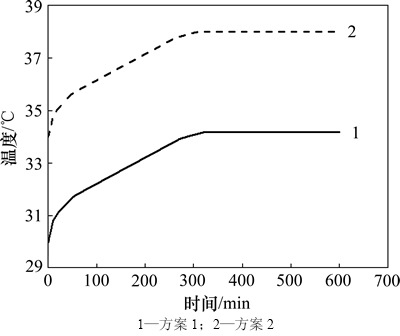
图8 不同选址方案避难硐室温度变化
Fig. 8 Temperatures change of different site selections
根据模型计算结果,避难硐室内温升3.8 ℃。若避难硐室内采用蓄冰空调制冷,蓄冰空调内冰的最低温度为-5 ℃,假定-5 ℃的冰全部转化为常温下的水,则需要的蓄冰量计算为4.2 m3。
5 结论
1) 建立了避难硐室温度计算模型,通过实验验证模型的合理性,并对模型进行修正,确定修正系数为0.97。
2) 对避难硐室内温度影响程度由大到小为壁面温度、岩石导热系数、原岩温度、调温圈半径,其极值R分别为10.994,6.411,2.635和0.393。
3) 壁面温度与平衡温度呈正线性相关,围岩导热系数与平衡温度呈负相关,且导热系数越小温升速率越快。
4) 所建立的温度计算模型及对温度影响因素的分析结果,可为避难硐室工程设计提供理论依据。
参考文献:
[1] 栗婧, 金龙哲, 汪声. 救生舱内氧含量舒适度研究[J]. 煤炭学报, 2013, 38(12): 2163-2167.
LI Jing, JIN Longzhe, WANG Sheng. Research on the comfort degree of oxygen content in refuge chamber[J]. Journal of China Coal Society, 2013, 38(12): 2163-2167.
[2] 夏才初, 张国柱, 肖素光. 考虑衬砌和隔热层的寒区隧道温度场解析解[J]. 岩石力学与工程学报, 2010, 29(9): 1767-1773.
XIA Caichu, ZHANG Guozhu, XIAO Suguang. Analytical solution to temperature fields of tunnel in cold region considering lining and insulation layer[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1767-1773.
[3] 徐学祖, 孙斌祥, 李东庆, 等. 边界温度周期波动下块石的温度变化规律[J]. 岩土工程学报, 2003, 25(1): 91-95.
XU Xuezu, SUN Binxiang, LI Dongqing, et al. Variation of temperature in ballasts under periodic fluctuation of boundary temperature[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(1): 91-95.
[4] 郭孝峰, 夏再忠, 吴静怡, 等. 埋地管道温度特性数值模拟与相似性实验研究[J]. 太阳能学报, 2010, 31(6): 727-731.
GUO Xiaofeng, XIA Zaizhong, WU Jingyi, et al. Similarities experiment and numerical simulation on the temperature characteristics of the pipeline underground[J]. Acta Energiae Solaris Sinica, 2010, 31(6): 727-731.
[5] 周志华, 张觉荣, 张士花. 土壤源热泵地埋管周围土壤温度变化规律研究[J]. 太阳能学报, 2009, 30(11): 1487-1490.
ZHOU Zhihua, ZHANG Juerong, ZHANG Shihua. The study of soil temperature change rule around buried pipes in ground- coupled source heat pump[J]. Acta Energiae Solaris Sinica, 2009, 30(11): 1487-1490.
[6] Barbaresi A, Torreggiani D, Benni S, et al. Underground cellar thermal simulation: Definition of a method for modelling performance assessment based on experimental calibration[J]. Energy and Buildings, 2014, 76(2): 363-372.
[7] Jenkins K, Gilbey M, Hall J, et al. Implications of climate change for thermal discomfort on underground railways[J]. Transportation Research Part D: Transport and Environment, 2014, 30(7): 1-9.
[8] Ampofo F, Maidment G, Missenden J. Underground railway environment in the UK Part 2: Investigation of heat load[J]. Applied Thermal Engineering, 2004, 24(5): 633-645.
[9] 肖琳, 杨成奎, 胡增辉, 等. 地铁隧道围岩内温度分布规律的模型试验及其热导率反算研究[J]. 岩土力学, 2010, 31(S2): 85-91.
XIAO Lin, YANG Chengkui, HU Zenghui, et al. Model test on temperature distribution in metro tunnel surrounding rock and inverse calculation of its thermal conductivity[J]. Rock and Soil Mechanics, 2010, 31(S2): 85-91.
[10] 邵珠山, 乔汝佳, 王新宇. 高地温隧道温度与热应力场的弹性理论解[J]. 岩土力学, 2013, 34(S1): 1-8.
SHAO Zhushan, QIAO Rujia, WANG Xinyu. Elasticity solution for temperature and stress fields of tunnels with high geothermal temperature[J]. Rock and Soil Mechanics, 2013, 34(S1): 1-8.
[11] 高建良, 徐文, 张学博. 围岩散热风流温度、湿度计算时水分蒸发的处理[J]. 煤炭学报, 2010, 35(6): 951-955.
GAO Jianliang, XU Wen, ZHANG Xuebo. Treatment of water evaporation during calculation of temperature and humidity of air flow cause d by heat release from surrounding rock[J]. Journal of China Coal Society, 2010, 35(6): 951-955
[12] 刘文杰, 缪小平, 丁静, 等. 北方地区浅埋人防工程热负荷特点[J]. 解放军理工大学学报(自然科学版), 2009, 10(S): 64-68.
LIU Wenjie, MIAO Xiaoping, DING Jing, et al. Numerical investigation of cooling (heating) load characteristics for shallow buried underground construction located in north area of China[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2009, 10(S): 64-68.
[13] 郭春香, 吴亚平, 董晟, 等. 热棒填土路基降温效果的三维非线性有限元分析[J]. 中南大学学报(自然科学版), 2014, 45(1): 202-207.
GUO Chunxiang, WU Yaping, DONG Sheng, et al. Three-dimensional nonlinear numerical analysis of cooling effect of thermosyphon on filling subgrade[J]. Journal of Central South University (Science and Technology), 2014, 45(1): 202-207.
[14] 吕伟新, 刘宝, 王磊. 煤矿爆炸后巷道内温度变化规律[J]. 哈尔滨工业大学学报, 2013, 45(5): 108-113.
L Xinwei, LIU Bao, WANG Lei. Research on temperature changing law after coal mine explosion in roadway[J]. Journal of Harbin Institute of Technology, 2013, 45(5): 108-113.
Xinwei, LIU Bao, WANG Lei. Research on temperature changing law after coal mine explosion in roadway[J]. Journal of Harbin Institute of Technology, 2013, 45(5): 108-113.
[15] 张小康, 何富连, 马恒. 矿井通风系统环境温度实时计算与应用[J]. 煤炭学报, 2012, 37(5): 863-867.
ZHANG Xiaokang, HE Fulian, MA Heng. Real-time calculation and application of mine ventilation system environmental temperature[J]. Journal of China Coal Society, 2012, 37(5): 863-867.
[16] 王海燕, 周心权. 平巷烟流滚退火烟羽流模型及其特征参数研究[J]. 煤炭学报, 2004, 29(2): 190-194.
WANG Haiyan, ZHOU Xinquan. Fire buoyant plume model and characteristic parameters of a reverse smoke in a horizontal airway during mine fire[J]. Journal of China Coal Society, 2004, 29(2): 190-194.
[17] 向立平, 王汉青. 空调客车内气流分布的人体热舒适性研究[J]. 中南大学学报(自然科学版), 2009, 40(5): 1194-1198.
XIANG Liping, WANG Hangqing. Thermal comfort based on air distribution in air-conditioning vehicle[J]. Journal of Central South University (Science and Technology), 2009, 40(5): 1194-1198.
[18] 王树刚, 徐哲, 张腾飞, 等. 矿井热环境人体热舒适性研究[J]. 煤炭学报, 2010, 35(1): 97-100.
WANG Shugang, XU Zhe, ZHENG Tengfei, et al. Human thermal comfort for mine environment[J]. Journal of China Coal Society, 2010, 35(1): 97-100.
(编辑 杨幼平)
收稿日期:2014-11-05;修回日期:2015-02-13
基金项目(Foundation item):“十二五”国家科技支撑计划基金资助项目(2012BAK09B00) (Project(2012BAK09B00) supported by the National Science and Technology Pillar Program during the 12th Five-year Plan Period)
通信作者:金龙哲,博士生导师,教授,从事矿山安全、应急救援研究;E-mail: lzjin@ustb.edu.cn