Trans. Nonferrous Met. Soc. China 25(2015) 3410-3420

Classification of mine blasts and microseismic events using starting-up features in seismograms

Guo-yan ZHAO, Ju MA, Long-jun DONG, Xi-bing LI, Guang-hui CHEN, Chu-xuan ZHANG

School of Resources and Safety Engineering, Central South University, Changsha 410083, China

Received 27 November 2014; accepted 10 June 2015

Abstract: To find discriminating features in seismograms for the classification of mine seismic events, signal databases of blasts and microseismic events were established based on manual identification. Criteria including the repetition of waveforms, tail decreasing, dominant frequency and occurrence time of day were considered in the establishment of the databases. Signals from databases of different types were drawn into a unified coordinate system. It is noticed that the starting-up angles of the two types tend to be concentrated into two different intervals. However, it is difficult to calculate the starting-up angle directly due to the inaccuracy of the P-wave arrival’s picking. The slope value of the starting-up trend line, which was obtained by linear regression, was proposed to substitute the angle. Two slope values associated with the coordinates of the first peak and the maximum peak were extracted as the characteristic parameters. A statistical model with correct discrimination rate of greater than 97.1% was established by applying the Fisher discriminant analysis.

Key words: microseismic event; mine blast; starting-up feature; Fisher discriminant analysis

1 Introduction

Microseismic events, with Richter magnitude from -3 to 3, refer to rockmass vibrations generated by fracturing or fluid disturbance. The microseismic monitoring technology, a geophysical approach, is used to monitor the status of underground structures. The distribution and its evolution of internal micro-cracking and deformations of the adjacent rock can be obtained by inversion analysis of the systems [1-3]. Microseismic monitoring technology has been rapidly developed in recent twenty years in the field of engineering geology, including tunneling, oil and gas exploration with hydraulic fracturing, nuclear waste disposal, as well as underground excavations existing potential hazards of room-and-pillar collapses and rockbursts. Applications of microseismic monitoring in China with their purposes are summarized in Table 1. Microseismic events, induced by the failure and deformation of rocks, can be located by developed methods [22-27]. On the other hand, from the micromechanical point of view, the particle simulation method [28-32] can be used to investigate the microseismic events in mines for monitoring its safety and stability.

Generally, there are always some problems existing in the applications of microseismic monitoring systems because of the complex mining systems, including background noise, useless data, and blasting signals admixture. As a result, providing intuitive monitoring data accurately becomes impossible. The daily summary of the Yongshaba Mine’s monitoring data signifies that more than half are rejected data. And the total number of blasts is nearly one third of the accepted microseismic events. Noise signals existing obvious characteristics can be easily discharged, the most difficult task to identify microseismic events from blasts. Since they share a large scale of intersection in the frequency distribution, to achieve recognition of the two types of events via simple spectral analysis is quite difficult.

Table 1 Some sites with microseismic monitoring system in China

Currently, some relatively effective identification methods are mainly dependent on the source parameters [33,34]. MALOVICHKO [35] selected the time of day, the repetition of waveforms, the high- frequency vs the low-frequency radiation and the radiation pattern as the discriminant features, then established the Gaussian maximum likelihood classification method for the classification. This method provides a way to identify signals of different types, but great amount of computation leads to low efficiency. VALLEJOS and MCKINNON [36] proposed the identification of seismic records in seismically active mines by considering the logistic regression and the neural network classification techniques. An efficient methodology was presented for applying these approaches to the classification of seismic records [36]. However, seismic parameters (local magnitude, corner frequency, seismic moment, moment magnitude, seismic energy, static stress drop, apparent stress, etc.) provided by the full-waveform systems require precise P and S-wave hand-picking, scilicet, expertise and time.

To determine discriminating features that are physically independent of each other, a blast signal database is established by field tests firstly and then a microseismic event database identified manually is built. Based on the two databases, six characteristic parameters from waveform starting-up analysis are extracted. By applying the Fisher discriminant analysis (FDA) to the characteristic parameters, a mathematical model that is able to correctly classify more than 97.1% blasts and microseismic events is established.

2 Database

2.1 Source of data

Seismic records from the site of Yongshaba Mine are used to identify the proposed method in this work. The Yongshaba orebody is a phosphate deposit, located in Guizhou, China. The mining method of blasthole with delayed backfill is used to extract the ore underground. The studied region covering a volume of approximately 3000 m × 300 m × 750 m, between 300 m and 700 m below the surface. Excavating multi-level simultaneously beneath the Jinyang Road is the principal situation nowadays. Potential hazards including landslides on the steeper surface, instability of the highway foundation and stope collapse are threating the safety to workers and residents. The underground microseismic monitoring system, used to inform the evolution of magnitude, temporal and spatial of the micro-fracture behavior, consists of 26 uniaxial and 2 triaxial velocimeters (Fig. 1).

2.2 Samples

The sample databases contain a total of 103 seismic records, from which 56 are labeled as normal events and the others are tagged as blasts. All of these seismic records are labeled manually. The usual practice of processing seismic data includes a qualitative or semi- quantitative classification of seismic events [35]. Four approaches to eliminate blasts from the seismic catalogue are applied in this study.

2.2.1 Repetition of waveforms

Blasts, especially stope firings, have multiple delays, which are expressed in the seismogram as similar signals repeating closely within a short time interval. The practice of decides whether an event is a blast or a microseismic event is based on the repetition feature. An example is shown in Fig. 2.

2.2.2 Tail and S wave

Commonly, seismograms capturing a blast will have a monotonically decreasing tail, which makes S wave arrival selection difficult to impossible. Seismograms capturing a microseismic events associated with shear fracturing will have an S-wave arrival more obviously than in the cases of blasts because the sources of the latter are usually in the focal mechanism of expansion and compression (Fig. 2).

2.2.3 Time of day

Another way to eliminate blasts from the microseismic catalogue is to apply time and/or spatial filters (i.e., events located close to blasts operating areas and/or at the blasting time are marked as blasts) [22]. Generally, mines have prescribed blasting time. The probability of an event being a blast is higher during these time. Two main daily blasting shifts are observed from the diurnal chart between 10:00 and 16:00 (stope firings) and 23:00 and 1:00 (development firings), each of which triggers an increase in seismicity (Fig. 3(a)).

2.2.4 Dominant frequency

A large number of actual observations and analysis show that blasts or explosions usually radiate higher frequency waves compared to normal microseismic events. Figure 3(b) shows that the amplitude spectra of the typical blast and microseismic event (presented in Fig. 2) reach up to 66.87 Hz and 22.11 Hz, respectively. The statistics data show that the values of the dominant frequency of the microseismic events varies from 10-100 Hz to 30-260 Hz for blasts at Yongshaba Mine.

3 Discriminating features

3.1 First trend line

Taking energy release rate into account, the waveform’s starting-up angle will vary between blasts and microseismic events. Figure 4(a) draws signals of blasts and microseismic events into a unified coordinate system. All waveform sections start at the point of each P-wave first arrival and end in their first peak points. Figure 4 shows huge differences existing in the time and amplitude distribution of the peak point within blasts and microseismic events. The statistical laws reflected by this figure also emphasize the importance of the waveform’s starting-up angle in identifying the two types of signal.

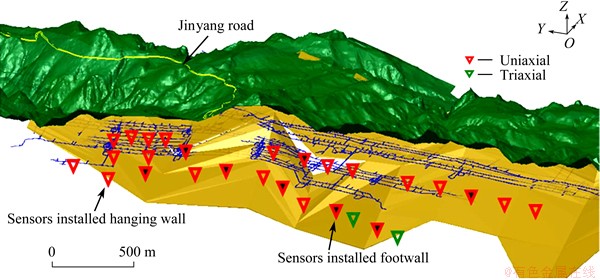
Fig. 1 Isometric view of orebody, tunnels and microseismic monitoring system at Yongshaba Mine

Fig. 2 Typical seismograms of first triggered sensor

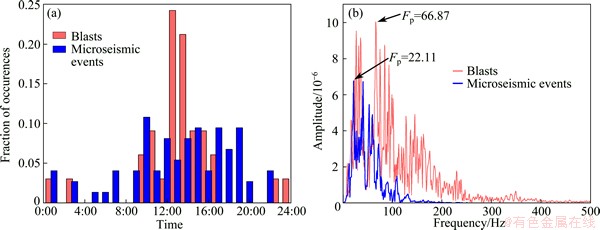
Fig. 3 Diurnal chart (a) and frequency distribution comparison of typical blast and microseismic event (b) at Yongshaba Mine

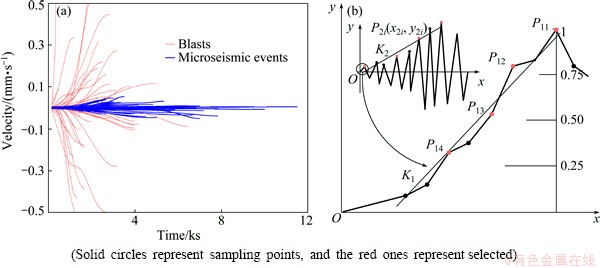
Fig. 4 Comparison chart of signal starting-up before first peak within blasts and microseismic events (a) and schematic diagram of data points selecting and trend line constructed by linear regression

However, connecting the starting point to the peak or any other sampling points directly to solve the starting-up angle is infeasible due to the picking inaccuracy of P-wave first arrival. The slope value of the starting-up trend line of the waveform is taken instead of the starting-up angle, that is, selecting appropriate sampling points on the waveform as data points for linear regression, and then using the slope value of the trend line calculated by least squares fitting instead of the starting-up angle.

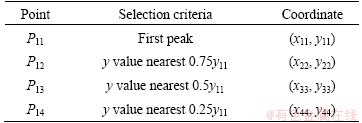
In accordance with the waveform’s shocking tendency, the data points are selected based on the distribution of amplitude axis (y), rather than on the time axis (x). Selection criteria and given coordinates of each points are shown in Fig. 4(b) and Table 2. As seen in Fig. 4(a), certain waveforms that maintain a smooth period at the beginning followed by a sharp ascent to the first peak exist. In that case, the four-point fitting method used in this work well circumvents the defects of fitting by all of the sampling points, meanwhile, improving the recognition performance.

Table 2 Data points selection criteria and given coordinate

The equation of the trend line can be expressed as

y=k₀+k₁x                                    (1)

where k₀ and k₁ are the parameters required solving. The least square estimators are those values of k₀ and k₁ that could minimize the function below:

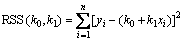               (2)

where n is the number of data points. When evaluated at , we call the quantity as the residual sum of squares. The least square estimates can be derived in many ways, one of which is given by the expressions:

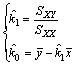                                (3)

where 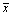 and  are the average values of x_1i and y_1i (i=1, 2, 3, 4), respectively. The codes S_XX and S_XY are calculated by equations:

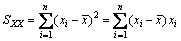                (4)

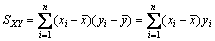           (5)

Setting K₁ as the slope value of the trend line calculated by Eq. (1) to Eq. (5) of the seismogram of the first triggered sensor by an event, and the logarithm of absolute value of K₁ is considered as the feature “first starting-up”. Figure 5(a) shows the comparison of lg K₁ within blasts and microseismic events retrieved from the already established databases.

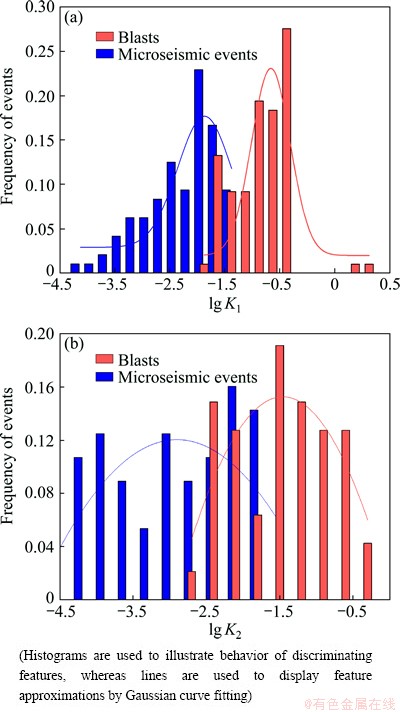
Fig. 5 Comparison chart of slope values of two starting-up trend lines within waveforms of blasts and microseismic events

3.2 Second trend line

Parameter k₂ is in similar calculation procedure with k₁. First of all, select the appropriate peaks on the same side of x axis with the maximum peak as data points. As shown in Fig. 4(b), 4 peaks, the maximum four peak and the peaks with y value nearest 0.75y₂₁, 0.5y₂₁, 0.25y₂₁, are selected. The slope value of the trend line before the maximum peak (the second trend line) is calculated using the least square estimates method. The logarithm of the absolute value of k₂ is considered as the feature “second starting-up”. Figure 5(b) shows the comparison of lg K₂ within blasts and microseismic events.

Figure 5 shows that “starting-up” performs well as discriminating features for the considered mines. The characteristic parameter lg k₁ provides the maximum separation between the populations of blasts and normal events. From Fig. 5(a), it is visible that normal events have average values of lg k₁ from -4.5 to -1.5, whereas blasts have values from -2.0 to -0.5. From Fig. 5(b), it is visible that normal events have average values of lg k₂ from -4.0 to -2.0, whereas blasts have values from -2.5 to -0.5.

4 Model building

4.1 Approach

The approach used in this research establishes the discriminator as a function of waveform parameters through the use of Fisher discriminant analysis (FDA). FDA is the method used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects. The classes of multi-dimensional data are projected onto a unique direction in order to make possible separation between the classes [37-40]. The Fisher discriminant analysis model of discriminant procedure is shown in Fig. 6. The performance of the discriminator is assessed by comparing the prediction outcomes of the model to known values.

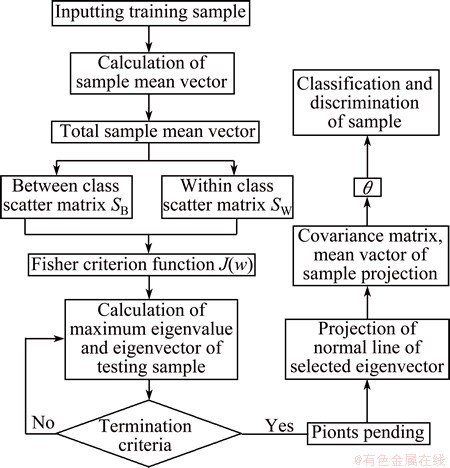
Fig. 6 Flow chart for application of Fisher discriminant analysis

Take the two classes of ω₁ and ω₂ to illustrate the principles of Fisher discriminant analysis. Define N as the number of observations, m as the number of variables, p as the number of classes, and N_j as the number of observations in the jth class. Represent the vector of variables for the ith observation as x_i. If the training data for all classes have already been stacked into the matrix X∈R^N×m, then the mean vector of the two classes in input space can be expressed as

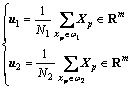                       (6)

Let the projection direction be:

ω=(ω₁, ω₂, …, ω_m)^T∈R^m                           (7)

The projections of the mean vector and the mean vector of total sample in this direction are

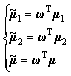                                 (8)

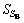Set and 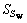to be the square sum of between-class scatter (S_B) and within-class scatter (S_W), which are respectively defined as

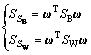                              (9)

and

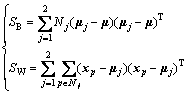              (10)

The Fisher discriminant analysis is aimed to make the ratio of the 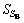to 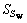as large as possible, namely:

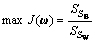                            (11)

The results deduced by Fisher are presented as

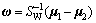                            (12)

Let θ be the classification threshold (generally calculated by the empirical formula), then the discriminant formulae are presented as

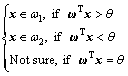                       (13)

4.2 Modeling

The aim of the present study is to establish a mathematical model for signal accurate identification of different classes of events using Fisher discriminant analysis. According to the analysis, parameters that characterize the tendency of the starting-up feature of waveform -lg k₁ and lg k₂ as well as coordinates of the first peak and the maximum peak which are also related to the energy release rate were chosen as inputting of training samples (Table 3). The FDA model for signal identification was established after developing the theory discussed above to the 103 sets of samples selected. The Fisher discriminant function generated has the following form:

F=-92.588lg x₁₁+3.878lg y₁₁-8.471lg k₁-3.704lg x₂₁-33.644lg y₂₁-4.304lg k₂-186.187   (14)

Equation (14), the canonical discriminant function, was used in the analysis. Table 4 shows that the discrimination capability of Eq. (14) is significant. The corresponding feature value of the discriminant function is 2.841 with variance ratio (discriminant efficiency) of 100%>85%. The correlation coefficient is as high as 0.860. So, it is concluded that the discriminant function can well distinguish the two categories through significance test.

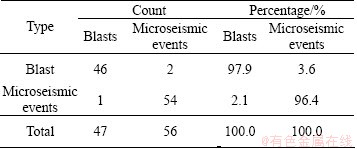
The test results on each back to the actual are listed in Table 5. It can be seen that more than 97.9% of original grouped cases are correctly classified by Fisher discriminant analysis method. Studies show that this method has a low misjudgment rate. The pretty good signal discriminant performance in blasts and microseismic events make it worthy of promotion in engineering applications.

5 Conclusions

1) Manual identification criteria, including the repetition of the waveforms, the tail decreasing, the occurrence time of day, and the dominant frequency have been summarized in detail. Signal databases of blasts and microseismic events were established based on the 4 manual identification criteria.

2) Two different intervals that the starting-up angles tend to be concentrated were noticed when signals from databases were drawn into a unified coordinate system.

Table 3 Training samples for model building

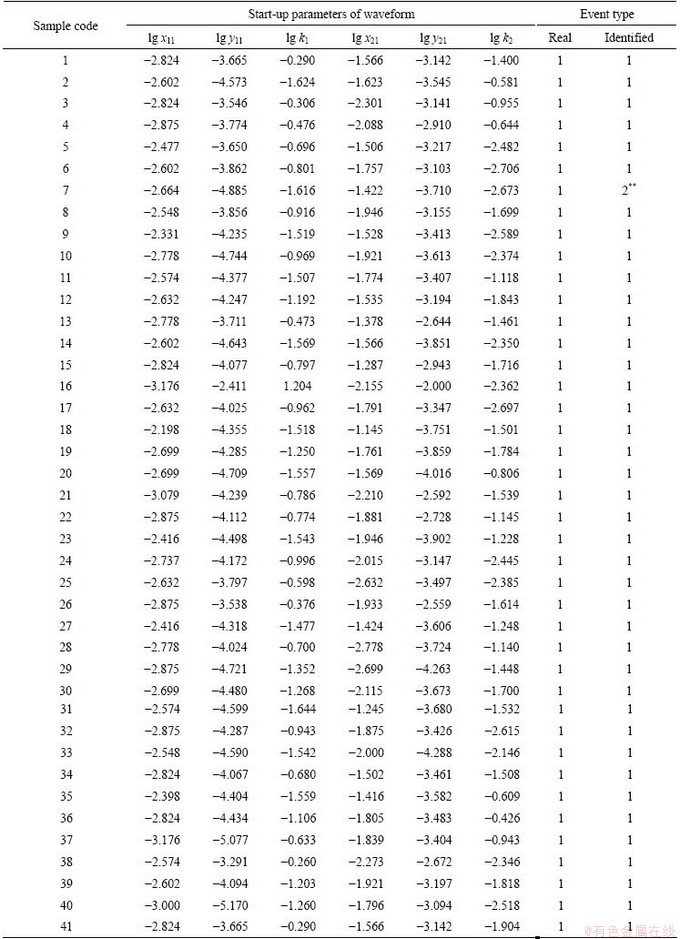
(to be continued)

(continued)

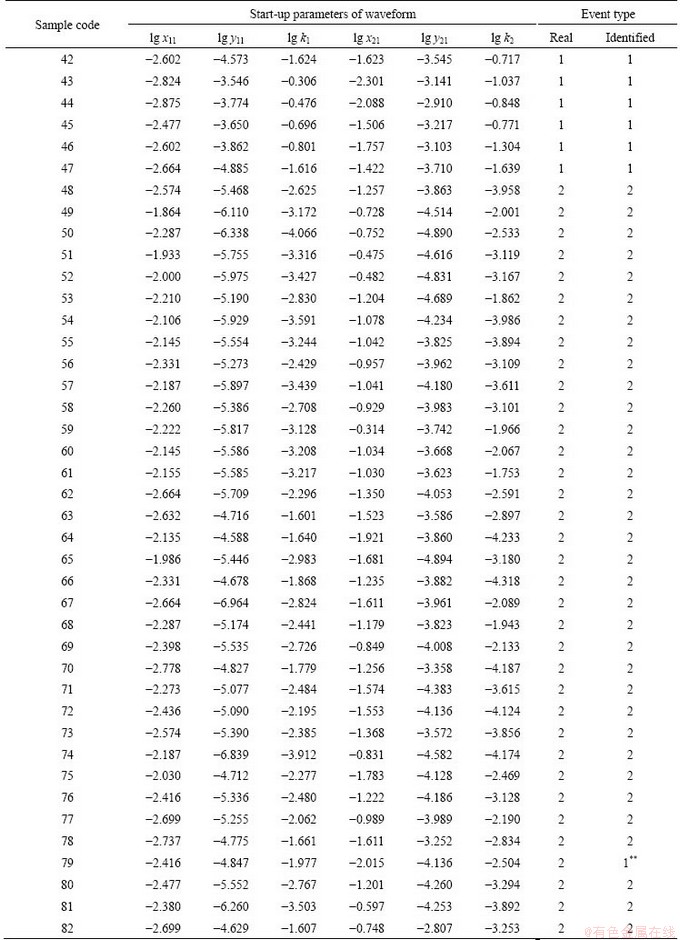
(to be continued)

(continued)

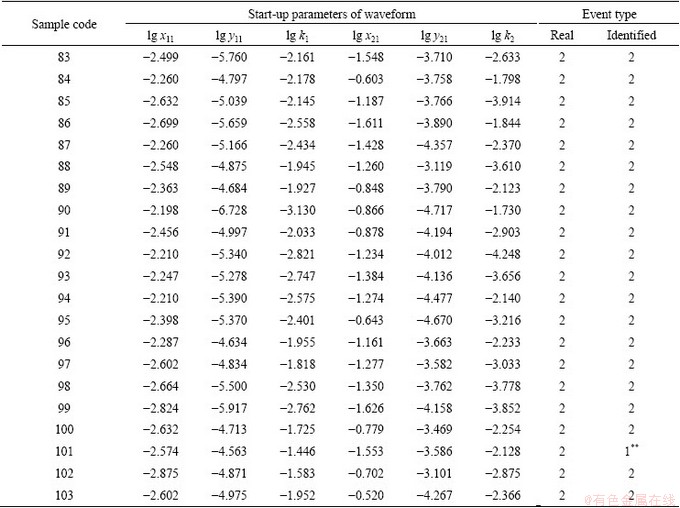
Table 4 Eigenvalue of Fisher discriminant function

Table 5 Classification results of events and blasts

3) Given P-wave first arrival’s picking inaccuracy, the coordinates and the slope value of starting-up trend line of first peak and maximum peak were extracted as characteristic parameters.

4) By applying the Fisher discriminant analysis to characteristic parameters extracted, a mathematical model that is able to correctly discriminate more than 97.9% blasts and microseismic events is established. Statistical results show that this method has a good performance in blasts and microseismic events discrimination. Moreover, the approach shows the advantage that the characteristic parameters would not be affected by P- and S-wave arrival picking when compared with discriminations based on source parameters.

References

[1] LIU Yun-long, TIAN You, FENG Xuan, ZHENG Que, CHI Huan-zhao. Review of microseismic technology and its application [J]. Progress in Geophysics, 2013, 28(4): 1801-1808.

[2] LI Shu-lin. Discuss on microseismic monitoring technology and its application to underground projects [J]. Chinese Journal of Underground Space and Engineering, 2009, 5(1): 122-128. (in Chinese)

[3] GE Mao-chen. Efficient mine microseismic monitoring [J]. International Journal of Coal Geology, 2005, 64(1): 44-56.

[4] LI Shu-lin, YIN Xian-gang, ZHENG Wen-da, CHZAR T. Research of multi-channel microseismic monitoring system and its application to Fankou lead-zinc mine [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2049-2055. (in Chinese )

[5] ZHAO Xing-dong, SHI Chang-yan, LIU Jian-po, LI Yuan-hui. Microseismic monitoring system establishment and its application study in Hongtoushan copper mine [J]. Journal of Northeastern University: Natural Science, 2008, 29(3): 399-403. (in Chinese )

[6] CHENG Yun-hai, JIANG Fu-xing, ZHANG Xing-min, MAO Zhong-yu, JI Zhen-wen. C-shaped strata spatial structure and stress field in longwall face monitored by microseismic monitoring [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 102-107. (in Chinese )

[7] TANG Li-zhong. Study on monitoring and prediction of seismicity and rockburst in a deep mine [D]. Changsha: Central South University, 2008. (in Chinese)

[8] LIU Xiao-hui, WU Ai-xiang, WANG Chun-lai, LI Rui, JI Xue-wen, LI Xiang, HUO Xiao-bin. Research on application of the microseismic monitoring system in Yunnan Huize Lead-zinc Mine [J]. Metalmine, 2010, (1): 151-158. (in Chinese)

[9] GUO Xian-zhang. The application of microseismic monitoring technique in jinan zhangmatun iron mine [D]. Shenyang: Northeastern University, 2008.

[10] XIE Xiao-dong, ZHANG Yin-liang, WANG Jin. Periodic weighting monitoring of main roof based on microseism monitoring system [J]. Zhongzhou Coal, 2011(3): 51-55. (in Chinese)

[11] JIANG Fu-xing. Microseismic monitoring study of rock fracture and catastrophe [D]. Beijing: Beijing University of Science and Technology, 2008. (in Chinese )

[12] WANG Yong, HOU Chun-hua, LI Fu-ping. Microseismic monitoring system sensors layout optimize research of Shirengou Iron Mine [J]. Express Information of Mining Industry, 2012(1): 120-124. (in Chinese )

[13] HU Jing-yun. Research of Theory and application of microseismic monitoring technology on large complex gob stability [D]. Changsha: Changsha Institute of Mining, 2011. (in Chinese )

[14] ZHANG Yin. Experimental study of prevention and treatment of rock burst by floor-break blasting [J]. Coal Technology, 2010, 29(10): 90-94. (in Chinese )

[15] DANG Bao-quan, LIU Chao. Discussion on sensors installing technology of micro-seismic monitoring system in xinzhuangzi colliery [J]. Coal Technology, 2010, 15(2): 87-91. (in Chinese )

[16] LI Xian-han. Researchand application on coal mine microseismic monitoring and web GIS [D]. Huainan: Anhui University of Science and Technology, 2010. (in Chinese )

[17] XU Nu-wen, TANG Chu-nan, SHA Chun, CIANG Z Z, YANG J Y. Microseismic monitoring system establishment and its engineering applications to left bank slope of Jinping I hydropower station [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 914-920. (in Chinese )

[18] Chang-guo, DOU Lin-ming, HE Jiang, SHAN Shi-ping, LIU Biao, GUO Xiao-qiang. Development and use of SOS microseismic monitoring system at Taoshan coal mine [J]. China Coal, 2010, 36(11): 86-90. (in Chinese )

[19] Hu Guang-jun, WU Jian-xing, ZHU Chao, ZHAO Zhi. Micro seismic real-time monitoring system applied in jinshandian iron mine [J]. Journal of Institute of Disaster-Prevention Science and Technology, 2011, 13(2): 28-33. (in Chinese)

[20] ZHANG Bo-hu, DENG Jian-hui, ZHOU Zhi-hui, LU Hong-xu, WU Ji-chang, WU Si-hao. Analysis of monitoring microseism in areas controlled by faults near powerhouse in Dagangshan hydropower station [J]. Rock and Soil Mechanics, 2012, 33(S2): s214-s220. (in Chinese)

[21] Central South University. Interim report of Yongshaba mine microseismic monitoring and early warning system [D]. Changsha: School of Resources and Safety Engineering, Central South University. (in Chinese)

[22] LI X B, DONG L J. An efficient closed-form solution for acoustic emission source location in three-dimensional structures [J]. AIP Advances, 2014, 4(2): 027110.

[23] DONG L J, LI X B, XIE G N. An analytical solution for acoustic emission source location for known P wave velocity system [J]. Mathematical Problems in Engineering, 2014, 2014: 290686.

[24] DONG Long-jun, LI Xi-bing. Three-dimensional analytical solution of acoustic emission or microseismic source location under cube monitoring network [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(12): 3087-3094.

[25] LI Qi-yue, DONG Long-jun, LI Xi-bing, YIN Zhi-qiang, LIU Xi-ling.Effects of sonic speed on location accuracy of acoustic emission source in rocks [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2719-2726.

[26] DONG L J, LI X B, ZHOU Z L, CHEN G H, MA J. Three-dimensional analytical solution of acoustic emission source location for cuboid monitoring network without pre-measured wave velocity [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(1): 293-302.

[27] DONG L J, LI X B. A microseismic/acoustic emission source location method using arrival times of PS waves for unknown velocity system [J]. International Journal of Distributed Sensor Networks, 2013, 2013: 307489.

[28] XIA M, ZHOU K. Particle simulation of the failure process of brittle rock under triaxial compression [J]. International Journal of Minerals, Metallurgy and Materials, 2010, 17(5): 507-513.

[29] XIA M, ZHAO C. Simulation of rock deformation and mechanical characteristics using clump parallel-bond models [J]. Journal of Central South University, 2014, 21(7): 2885-2893.

[30] XIA M, ZHAO C, HOBBS B E. Particle simulation of thermally- induced rock damage with consideration of temperature-dependent elastic modulus and strength [J]. Computers and Geotechnics, 2014, 55: 461-473.

[31] XIA M. Thermo-mechanical coupled particle model for rock [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(7): 2367-2379.

[32] XIA M. An upscale theory of thermal-mechanical coupling particle simulation for non-isothermal problems in two-dimensional quasi- static system [J]. Engineering Computations, 2015, 32(7): 2136-2165.

[33] DONG L J, WESSELOO J, POTVIN Y, L I X. Discrimination of mine seismic events and blasts using the fisher classifier, bayesian classifier and logistic regression [J]. Rock Mech Rock Eng, 2015: 1-29, doi: 10.1007/s00603-015-0733-y.

[34] DONG L J, LI X B, XIE G N. Nonlinear methodologies for identifying seismic event and nuclear explosion using random forest, support vector machine, and naive bayes classification [J]. Abstract and Applied Analysis, 2014, 2014: 459137.

[35] MALOVICHKO D. Discrimination of blasts in mine seismology [C]//Proceeding of the deep mining 2012, Perth: Australian Centre for Geomechanics, 2012: 123-130.

[36] VALLEJOS J A, MCKINNON S D. Logistic regression and neural network classification of seismic records [J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 62: 86-95.

[37] Sanford weisberg. Applied linear regression [M]. 3rd ed. New Jersey: John Wiley & Sons, 2005: 23-24.

[38] DONG Long-jun, LI Xi-bing, ZHAO Guo-yan, GONG Feng-qiang. Fisher discriminant analysis model and its application to predicting destructive effect of masonry structure under blasting vibration of open-pit mine [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 750-758. (in Chinese)

[39] DONG Long-jun, LI Xi-bing, PENG Kang. Prediction of rockburst classification using random forest [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(2): 472-477.

[40] DONG L J, LI X B. Comprehensive models for evaluating rockmassstability based on statistical comparisons of multiple classifiers [J]. Mathematical Problems in Engineering, 2013, 2013: 395096.

基于波形起振特征的矿山微震与爆破信号模式识别

赵国彦，马 举，董陇军，李夕兵，陈光辉，张楚旋

中南大学 资源与安全工程学院，长沙 410083

摘  要：为探寻能够区分矿山微震信号和爆破信号的波形特征，建立基于人工识别标准的事件数据库。人工识别的考虑因素包括：波形的重复特征、波形的衰减特征、信号的主频大小以及事件发生的具体时间。将数据库中的微震信号和爆破信号调整至同一坐标系下发现，两类事件的起振角趋。于集中在不同的区间。考虑到P波到时提取的不准确性，波形起振角难以准确计算，提出以应用线性回归拟合得到的起振趋势线斜率代替起振角。将首次峰值起振趋势线斜率和最大峰值起振趋势线斜率连同首次波峰及最大波峰的坐标列为特征参数，应用Fisher判别法，能成功实现微震事件与爆破时间的准确分离，识别正确率达到97.1%。

关键词：微震事件；矿山爆破；起振特征；Fisher判别

(Edited by Yun-bin HE)

Foundation item: Projects (51374244, 11447241) supported by the National Natural Science Foundation of China

Corresponding author: Long-jun DONG; Tel: +86-13973160861; E-mail: rydong001@csu.edu.cn

DOI: 10.1016/S1003-6326(15)63976-0