用于岩土极限分析的非线性能量耗散理论
杨小礼
( 中南大学 土木建筑学院,湖南 长沙,410075 )
摘要: 在岩土工程中广泛应用Mohr-Coulomb或Tresca破坏准则,该破坏准则为线性破坏准则。然而,大量的岩土试验结果表明:岩土破坏准则是非线性的,而线性破坏准则只是其中的一个特例。在上限定理的基础上,提出用于岩土极限分析的非线性能量耗散理论,并从应用方面证明该理论的正确性。研究结果表明:对于一般边坡稳定性,应用该理论所得结果与应用变分法所得结果一致;对于存在竖直裂缝的边坡稳定性,应用该理论所得结果与下限解一致;对主动或被动土压力,应用该理论所得结果与广义Rankine解一致。
关键词: 非线性破坏准则; 极限分析; 边坡稳定性; 土压力
中图分类号:TU43 文献标识码:A 文章编号: 1672-7207(2005)04-0710-05
Nonlinear energy dissipation theory for limit analysis in geotechnical engineering
YANG Xiao-li
(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract: Linear Mohr-Coulomb and Tresca failure criteria are widely used in geotechnical engineering. However, the experimental results show that the strength envelopes of almost all geomaterials have the nature of nonlinearity, and that linear Mohr-Coulomb failure criterion is a special case of failure criteria. According to the nonlinear failure criterion, nonlinear theory for limit analysis was proposed. From the numerical results, it is found that the solutions using the new theory agree well with the solutions using variational calculus method for general slopes, that the solutions using the new theory agree well with the solutions using lower bound theorem for vertical cut, and that the solutions using the new theory agree well with the solution of the active and passive earth pressures using the extended Rankine solution for rigid retaining walls.
Key words: nonlinear failure criterion; limit analysis; slope stability; earth pressure
1975年,以W.F.Chen[1]的专著《Limit Analysis and Soil Plasticity》问世为标志,产生了岩土极限分析法这门新的学科分支。几十年来,它得到了突飞猛进的发展,在城乡建筑、铁路公路、水利水电、港口、机场及矿山等工程建设中发挥着重要作用。
极限分析法建立在虚功原理的基础上,该方法包括上限定理和下限定理。运用上限定理,建立机动容许的速度场;根据外力所做的功率与能量沿速度间断线耗散功率以及能量在变形体上耗散功率之和相等的原理求出荷载,该荷载为岩土结构物在失稳破坏时所承受真实荷载的上限,即大于或等于真实极限荷载。在很多机动容许的速度场中寻找尽可能小的荷载。同理,运用下限定理,建立应力平衡场,根据力的平衡条件,求出极限荷载或稳定性系数的下限,该解为真实解的下限,即小于或等于真实解。在很多应力平衡场中寻找尽可能大的解。运用这2个定理,可以确定岩土结构物真实极限荷载的范围。
1 问题的提出
虚功率原理表明:对于任意一组静力容许的应力场和任意一组机动容许的速度场,外力的虚功率等于物体内能消散功率。由虚功率原理可推导上限定理为:在所有机动容许的塑性变形速度场相对应的荷载中,极限荷载为最小[1],即
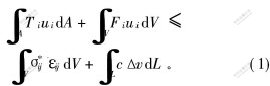
其中:Ti和Fi分别为作用物体上的面力和体力;σ*ij为由应变速率[AKε·]ij按塑性变形法则求出的应力;ui和[AKε·]ij分别为速度场中的速度和应变速率;A为荷载作用的面积;V为物体的体积;L为速度间断线;Δv为速度间断线两侧切向速度变化量;c为岩土抗剪强度指标,由线性Mohr—Coulomb破坏准则确定。在线性Mohr-Coulomb破坏准则中,岩土最大主应力和最小主应力的关系为线性关系,其表达式为:
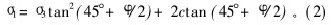
其中:σ1和σ3分别为岩土破坏时的最大和最小主应力。由式(2)可看出,σ1和σ3的关系为线性关系。但是,许多实验结果表明,受到破坏时岩土的最大主应力和最小主应力的关系为非线性关系,而线性关系是其中的一个特例。1966年D.Hobbs[2]提出Power law非线性强度准则;B.Ladanyi[3]在Griffith裂纹理论的基础上提出新的非线性准则;E.Hoek等[4]根据前人大量岩石实验结果,总结出著名的Hoek-Brown破坏准则,即
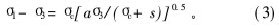
其中:a和σc+s为由实验确定的岩石参数。
从式(3)可看出σ1和σ3的关系也为非线性关系。后来,E.Hoek等[5]对式(3)进行修正,得出如下破坏准则:
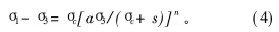
其中:n为由实验确定的岩石参数。在不同的侧限条件下,F.Santarelli[6]及J.G.Agar等[7]分别对不同的岩土介质进行三轴实验,结果表明:岩土受到破坏时,屈服面上的最大主应力与侧限压力(最小主应力)的关系也为非线性关系。R.Baker[8]对不同的土体进行三轴实验,发现破坏准则也是非线性的。
在非线性破坏准则下,岩土结构物承载力或稳定性的极限分析问题一直是岩土工程界的难点之一。R.Baker等[9]运用非线性破坏准则,在变分原理的基础上,对边坡附近的条形基础进行上限分析。但只给出了变分控制方程组,而未对其进行求解。后来,X.J.Zhang等[10]也在变分原理的基础上,采用“逆算法”研究边坡在非线性破坏准则下的滑动面形状,并给出边坡在各种坡角下的稳定性系数。但是,绝大部分研究者采用线性Mohr-Coulomb破坏准则,这是因为:
a. 在岩土介质中应用的上限定理和下限定理是建立在线性Mohr-Coulomb破坏准则基础上,即2个定理公式中所含的强度指标是线性Mohr-Coulomb破坏准则下的强度指标,即抗剪强度指标的值为已知。
b. 线性Mohr-Coulomb破坏准则可表示成圆域,在形成规划方程时,便于采用外切或内接正多边形方法;而非线性破坏准则不能以圆域表示,无法采用外切正多边形方法。
c. 非线性破坏准则下的上限目标函数为非光滑函数,如果处理计算不当,就不能得到最优的上限解。
当岩土服从非线性破坏准则时,抗剪强度指标c和φ的值为未知,如何在极限分析中应用非线性破坏准则是目前岩土工程界的难题[11]。
2 非线性能量耗散理论
在进行上限分析时,若所选择的机动容许的速度场满足速度边界条件和速度相容条件,即可求出问题的上限解。上限值的大小与速度场选择密切相关,只要速度场选择合理,就有可能求出问题的精确解或真实解。此外,几种不同的速度场对应的上限解可能相同或几乎相同,在选择速度场时应尽量使速度场简单,上限解较小;速度场的选择与土体的抗剪强度指标、土体破坏准则之间没有必然的联系。
在进行结构的上限分析时,提高材料的屈服强度不会降低结构的极限载荷,线性Mohr-Coulomb破坏准则可表示为一个圆域,为了便于进行问题的上限分析,许多研究作者采用外切正多边形方法,此方法实际上提高了材料的屈服强度。因此,若所选择的屈服强度超过岩土材料的真实屈服强度时,则在该屈服强度下,任一机动容许速度场对应的上限解均为极限载荷(对应真实的屈服强度)的上限。
基于上述指导思想,在对非线性破坏准则下的上限进行分析时,可采用“外切直线法”研究结构物的上限解,以提高岩土材料强度。设岩土材料非线性破坏准则为:
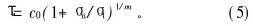
其中:c0,σt和m为岩土材料参数,由三轴试验确定。将式(5)绘制成曲线,如图1所示。图1中,c0表示曲线与纵轴的截距,当m=1时,式(5)则为线性Mohr-Coulomb破坏准则。对于图1中由切线确定的线性破坏准则,若曲线的曲率随σn的增加而逐步减少,则切线完全位于曲线的外侧,位于切线破坏准则上的所有点所对应的材料强度相对提高。因此,在外切线破坏准则下的上限解必定为真实极限载荷(非线性破坏准则对应的极限载荷)的上限。
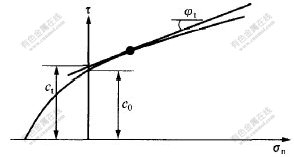
图 1 非线性破坏准则的切线
Fig. 1 Tangential line to nonlinear failure criterion
式(5)的切线方程为:
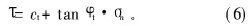
其中:ct和tanφt分别表示切线的截距和斜率。ct的表达式为:
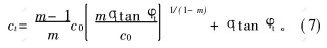
根据上述分析,岩土极限分析的非线性能量耗散理论可描述为:以切线方程代替非线性破坏准则,计算外力的功率与内能耗散,在整个单刚块或多刚块破坏机理中强度参数φt和ct的值保持不变,作用在各刚块上的正应力σn和剪应力τ相同,但大小未知。当岩土结构物破坏时,能量平衡体系耗散功率最小,以此确定切线方程的切点位置和岩土结构物的承载力或稳定性。
3 非线性能量耗散理论的有效性
为了证明非线性能量耗散理论的有效性,从边坡稳定性和土压力2个方面进行研究。
3.1 边坡稳定性的比较
对于一般边坡,根据岩土极限分析非线性能量耗散理论,计算非线性破坏准则下的边坡稳定性系数,所得结果与X.J.Zhang等[10]采用变分法所得结果一致,证明作者所提出的非线性能量耗散理论的有效性和正确性。上限解总是大于或等于问题的真实解,下限解总小于或等于问题的真实解。对于不能抗拉竖直边坡,应用该理论所得的下限解与上限解相等,进一步证明了所提出的非线性能量耗散理论的正确性[12-19]。
3.2 挡土墙土压力的比较
为了检验极限分析非线性能量耗散理论的有效性与正确性,对竖直及光滑的挡墙,墙高为H,在填土面水平的条件下,采用岩土极限分析非线性能量耗散理论和广义Rankine理论公式进行计算,将计算结果进行比较。对于如图2所示的被动土压力问题(刚体ABC沿滑动面向上滑动)及如图3所示的主动土压力问题(刚体ABC沿滑动面向下滑动),其计算结果如表1和表2所示。由表1和表2可知,2种方法的计算结果完全相等,证明了非线性能量耗散理论的有效性和正确性。
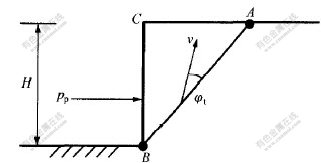
图 2 被动土压力的速度场
Fig. 2 Velocity field for passive earth pressure
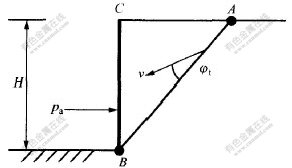
图 3 主动土压力的速度场
Fig. 3 Velocity field for active earth pressure
表 1 被动土压力的上限解与广义Rankine解的比较
Table 1 Comparisons of passive earth pressure between upper bound and extended Rankine solutions

表 2 主动土压力的上限解与广义Rankine解的比较
Table 2 Comparisons of active earth pressure between upper bound and extended Rankine solutions

岩土极限分析非线性能量耗散理论解决了岩土工程界的破坏准则非线性问题。目前,岩石边坡稳定性分析、岩石地基承载力计算都采用线性Mohr-Coulomb破坏准则,即计算时采用c和φ抗剪强度指标。实际上,大量实验成果证实岩石破坏服从Hoek-Brown非线性破坏准则。即抗剪强度指标c和φ的值未知。在极限分析的基础上,如何根据Hoek-Brown破坏准则计算边坡的稳定性和地基的承载力,国内外尚无公认可行的方法。新理论解决了这一难题。当土体破坏服从非线性破坏准则时,岩土极限分析非线性能量耗散理论解决了土坡稳定性问题、挡土墙土压力问题以及地基承载力问题。非线性破坏准则包含线性Mohr-Coulomb破坏准则,即线性Mohr-Coulomb破坏准则是非线性破坏准则的一个特例。
4 结 论
a. 传统的岩土极限分析建立在线性Mohr-Coulomb破坏准则的基础上,大量实验结果证明岩石破坏服从非线性Hoek-Brown破坏准则,即c和φ值未知。在极限分析理论的基础上,如何根据非线性破坏准则计算稳定性或承载力,目前国内外没有一个公认可行的方法。作者所提出的岩土极限分析非线性能量耗散理论,为解决了这一难题开辟了有效途径。
b. 应用该理论所得结果与应用变分法所得结果一致;对于存在竖直裂缝的边坡稳定性,应用该理论所得结果与下限解一致;对主动或被动土压力,应用该理论所得结果与广义Rankine解一致,从而从边坡稳定性和地基承载方面证明了该理论的有效性。
参考文献:
[1]Chen W F. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier Science, 1975.
[2]Hobbs D. A study of the behaviour of broken rock under triaxial compression and its application to mine roadways[J]. International Journal of Rock Mechanics and Mining Sciences, 1966, 3(1): 11-43.
[3]Ladanyi B. Use of the long-term strength concept in the determination of ground pressure of tunnel lining[A]. Proceeding of the 3rd Congress of International Society of Rock Mechanics on Advances in Rock Mechanics[C]. Washington: National Academy of Science, 1974: 1150-1156.
[4]Hoek E, Brown E T. Empirical strength criterion for rock masses[J]. ASCE Journal of Geotechnical Engineering, 1980, 106(9): 1013-1036.
[5]Hoek E, Brown E T. Practical estimate the rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.
[6]Santarelli F. Theoretical and experimental investigation of the stability of the axisymmetric borehole[D]. London: University of London, 1987.
[7]Agar J G, Morgenstern N R, Scott J. Shear strength and stress-strain behaviour of Athabasca oil sand at elevated temperatures and pressure[J]. Canadian Geotechnical Journal, 1985, 24(1): 1-10.
[8]Baker R. Nonlinear Mohr envelopes based on triaxial data[J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130 (5): 498-506.
[9]Baker R, Frydman S. Upper bound limit analysis of soil with nonlinear failure criterion[J]. Soils and Foundations, 1983, 23(4): 34-42.
[10]Zhang X J, Chen W F. Stability analysis of slopes with general nonlinear failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33-50.
[11]Jiang G L. Non-linear finite element formulation of kinematic limit analysis[J]. International Journal for Numerical Methods in Engineering, 1995, 38(16): 2775-2807.
[12]YANG Xiao-li, LI Liang, YIN Jian-hua. Seismic and static stability analysis of rock slopes by a kinematical approach[J]. Geotechnique, 2004, 54(8): 543-549.
[13]YANG Xiao-li, LI Liang, YIN Jian-hua. Stability analysis of rock slopes with a modified hoek-brown failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(2): 181-190.
[14]YANG Xiao-li, YIN Jian-hua. Slope stability analysis with nonlinear failure criterion[J]. ASCE Journal of Engineering Mechanics, 2004, 130(3): 267-273.
[15]YANG Xiao-li, YIN Jian-hua, LI Liang. Influence of a nonlinear failure criterion on the bearing capacity of a strip footing resting on rock mass using a lower bound approach[J]. Canadian Geotechnical Journal, 2003, 40(3): 702-707.
[16]YANG Xiao-li, YIN Jian-hua. Upper bound solution for ultimate bearing capacity with a modified hoek-brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 550-560.
[17]YANG Xiao-li. Unified strength solution for geotechnical structure reinforced by geotextile[J]. Journal of Structural Engineering, 2003, 30(2): 115-118.
[18]YANG Xiao-li, XU Lin-rong, LI Liang, et al. Effects of intermediate principal stress on the displacement around tunnels in visco-elastoplastic rock[J]. Journal of the Southeast Asian Geotechnical Society, 2002, 33(2): 87-92.
[19]杨小礼,李亮,刘宝琛. 非线性破坏准则对被动土压力的影响[J].工程力学, 2004, 21(1): 31-36.
YANG Xiao-li, LI Liang, LIU Bao-chen. Influences of a nonlinear failure criterion on passive earth pressure[J]. Engineering Mechanics, 2004, 21(1): 31-36.
收稿日期:2004-11-15
基金项目:国家自然科学基金资助项目(50408020);中国博士后科学基金资助项目(2003034468)
作者简介:杨小礼(1970-),男,博士后,副教授,从事岩土与隧道工程研究
论文联系人: 杨小礼,男,博士后,副教授;电话:0731-2656248(O);E-mail:yangxl@mail.csu.edu.cn