J. Cent. South Univ. (2021) 28: 968-980

DOI: https://doi.org/10.1007/s11771-021-4657-2

Dynamic response limit of high-speed railway bridge under earthquake considering running safety performance of train

LIU Xiang(刘祥)¹, JIANG Li-zhong(蒋丽忠)^{1, 2}, XIANG Ping(向平)^{1, 2}, LAI Zhi-peng(赖智鹏)^{1, 2},FENG Yu-lin(冯玉林)³, CAO Shan-shan(曹珊珊)⁴

1. School of Civil Engineering, Central South University, Changsha 410075, China;

2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;

3. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China;

4. Guangdong Transportation Technology Testing Co., Ltd., Guangzhou 510550, China

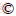Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract: Due to the wide railway network and different characteristics of many earthquake zones in China, considering the running safety performance of trains (RSPT) in the design of high-speed railway bridge structures is very necessary. In this study, in order to provide the seismic design and evaluation measure of the bridge structure based on the RSPT, a calculation model of RSPT on bridge under earthquake was established, and the track surface response measure when the derailment coefficient reaches the limit value was calculated by referring to 15 commonly used ground motion (GM) intensity measures. Based on the coefficient of variation of the limit value obtained from multiple GM samples, the optimal measures were selected. Finally, the limit value of bridge seismic response based on RSPT with different train speeds and structural periods was determined.

Key words: high-speed railway bridge; seismic design; running safety performance; measure limit

Cite this article as: LIU Xiang, JIANG Li-zhong, XIANG Ping, LAI Zhi-peng, FENG Yu-lin, CAO Shan-shan. Dynamic response limit of high-speed railway bridge under earthquake considering running safety performance of train [J]. Journal of Central South University, 2021, 28(3): 968-980. DOI: https://doi.org/10.1007/s11771-021-4657-2.

1 Introduction

China is located between the circum-Pacific seismic belt and the Eurasian seismic belt, which are the two major seismic belts in the world. It is squeezed by the Pacific plate, India plate, and Philippine Sea plate, and the seismic fault zone is very active. Earthquakes in China are mainly distributed in 23 seismic belts in five regions: Taiwan Province, Southwest China, Northwest China, North China, and Southeast coastal areas. Railway is an important transportation project [1-3]. In addition, China’s high-speed railway (HSR) planning ranges are wide, and most of them are “bridge instead of road” [4-8], and earthquakes can damage to the bridge structure [9, 10], such as displacement of girder, displacement and overtuning of bearing, cracking and spalling of pier concrete, and abutment sliding with foundation. And relatively strong earthquake will affect the safety of train operation and even lead to secondary disasters when the train rushes down the bridge. In Japan, earthquakes have also caused train derailments on bridges [11].

At present, the relevant codes in China have set some requirements for the seismic design of HSR bridges considering trains. However, they mainly consider the seismic performance of the bridge itself and enough consideration has not been given to the running safety performance of trains (RSPT) on the bridge during earthquake [12]; or only control the bridge deck deformation to cause rail deformation [13], to ensure the RSPT passing through the beam end. However, during the earthquake, the RSPT is affected by not only the rail deformation, but also derailing or overturning due to the large amplitude vibration of the track- bridge structures. The seismic design requirements of HSR bridges for RSPT in China are still insufficient, and there is no evaluation standard for RSPT on the bridge during earthquake. In addition, HSR bridge designer cannot carry out complex train-bridge coupling calculation to evaluate the safety of trains during earthquake.

The RSPT on bridges during earthquake has been extensively investigated and significant achievement has been made in this direction. JU et al [14] thoroughly investigated the RSPT during earthquake and proposed an efficient calculation method for wheel rail contact. This wheel-rail calculation method can simulate the wheel rail separation, and based on this method, they analyzed the RSPT during earthquake considering liquefaction of sand [15], investigated measures to improve seismic performance of bridge based on RSPT and non-linear dynamic performance of train-bridge coupled system during earthquake [16]. YAU et al [17] and WU et al [18] used simple models to discuss the stability of bridges and trains under earthquake. MONTENEGRO et al [19] considered the damage of bearing after earthquake action by equivalent linearization method and evaluated the RSPT on the bridge during earthquake. ZENG et al [20], XU et al [21], and ZHANG et al [22] analyzed the system response of the train-bridge and RSPT based on random dynamic theory. ZENG et al [11] took advantage of linear complementarity problem to analyze the RSPT and bridge dynamics considering nonlinear wheel-rail contact. DU et al [23] discussed the input method of non-uniform excitation for long-span bridges under earthquake. JIN et al [24] discussed the effect of vertical earthquake on RSPT on bridge. ZHU et al [25] analyzed the effect of heavy haul train on the dynamic response of cable-stayed bridge under earthquake. JIANG et al [26, 27] established the train-bridge coupling model for discussing the applicability of HSR track bridge system in near fault earthquake. NISHIMURA et al [28] and TANABE et al [29] proposed and developed a calculation method and program for evaluating RSPT on bridge during earthquake. Some researchers proposed the approach to improve RSPT. MIYAMOTO et al [30] and MATSUMOTO et al [31] focused on vehicle improvement bridge structure improvement, respectively. Shaking table tests of train derailment under earthquake have been reported in Refs. [32, 33]. These reports mainly discussed the calculation methods of the coupling vibration of the train- bridge or the RSPT during the earthquake and do not provide a clear evaluation measure of the RSPT on the bridge. Calculating the vibration of train-bridge system under earthquake action to ensure the RSPT is too cumbersome for engineering designers, thus greatly affecting the efficiency. Therefore, bridge seismic design based on RSPT needs a set of relatively simple evaluation measures. LUO et al [34, 35] proposed a simple calculation theory of RSPT introducing the peak velocity (PV) and velocity spectral intensity (SI) on the track surface as the bridge design limited measures considering the RSPT.

This paper aims at providing a convenient design measure to evaluate the seismic performance of HSR bridge based on RSPT. To choose the dynamic limit measure reasonably reflecting the bridge dynamic response under the earthquake action based on the RSPT, multiple seismic waves were selected to calculate the coefficient of variation (COV) of bridge limit response measure under train derailment condition (according to derailment coefficient), and the minimum COV measure was used as the optimal measures, and this method was used as the evaluation standard of optimum measure [35]. Finally, according to the track surface response, the seismic measures limit of HSR bridge based on RSPT was proposed.

2 Calculation model

The RSPT on bridges under earthquake action was analyzed by a dynamic model train-bridge system, in which the train was simulated by the multi-rigid body dynamic theory [36-41]. The train was run in a straight line, i.e., the train running out of the line or overturning was not considered. Each car-body, bogie has five degrees of freedom (DOF), including lateral, vertical, roll yaw and pitch; each wheelset has four DOFs, including lateral, vertical, roll and pitch, as shown in Figure 1, where t₁ and t₂ denote the front and rear bogie, respectively; w_i denotes the i-th wheelset; d₁ denotes the half spacing between two wheelsets of the same bogie; d₂ denotes the half spacing between two bogies; h₁ denotes the spacing between the center of gravity of the car body and the secondary suspension; h₂ denotes the spacing between the secondary suspension and the bogie; h₃ denotes the spacing between the bogie and and the primary suspension; k and c denote the stiffness and damping of spring, respectively; and the subscripts p and s denote the primary and secondary suspension, respectively. According to the energy variation principle [42], the dynamic equation of the train can expressed by Eq. (1):

               (1)

where M^V, C^V and K^V are, respectively, the mass, damping, and stiffness of the train; F^V is the force vector of the train, including its own gravity, wheel rail interaction force and seismic force.

The bridges were configured as the 32 m multi-span simple-supported bridge and simulated by the finite element theory. In this study, only the input acceleration from the transverse direction of the bridge was considered the seismic excitation. Because of the high speed of the train and the long duration of GM, to reduce the corresponding DOF under reasonable circumstances, the pier was considered equivalent to a single DOF system along the transverse direction of the bridge [43], and the mass and stiffness of the track system were superimposed on the DOF in the main girder. The dynamic equation of the bridge is represented by Eq. (2):

                (2)

where M^B, C^B and K^B are the mass, damping, and stiffness of bridge, respectively; F^B is the force vector of the bridge, including wheel-rail contact force and seismic force.

The wheel-rail contact produces normal force and creep force of wheel-rail. The train and track bridge structures were coupled into a large system through the wheel-rail contact. In this study, the knife-edge contact constraints were used to overcome the wheel-rail contact problem [11, 44, 45]. The tread was an ideal cone, and the rail was regarded as a hinge point, as shown in Figure 2; the lateral clearance between the wheel and rail was 10 mm, and the lateral contact stiffness k_ry was 1.617×10⁷ N/m [45].

The wheel-rail vertical force (P_hz) was calculated by the Hertz contact theory, which can be expressed as following:

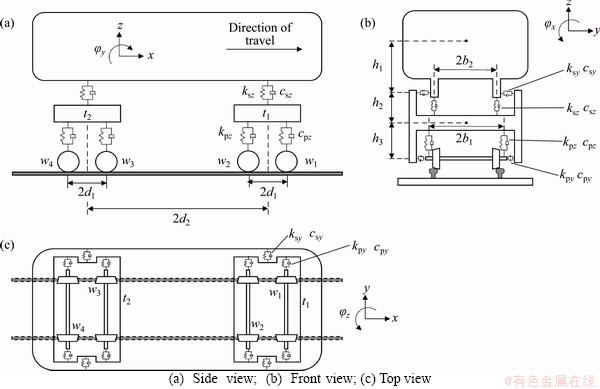
Figure 1 Train model:

Figure 2 Knife-edge contact

                            (3)

where G is the contact constant and △_wr is the relative compression of the wheel and rail. According to the displacement relationship, the compression of Hertz spring can be obtained by simplified calculation represented by Eq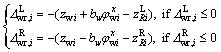. (4):

         (4)

where the subscript i represents the i-th wheelset and the corresponding rail position; the superscripts R and L represent the right and left rails, respectively; z_wi denotes the vertical displacement of i-th wheelset;andare the vertical displacement of the left and right rail, respectively (Figure 3).

Figure 3 Wheel-rail geometric state

Through the wheel-rail contact, the dynamic equation of the system can be obtained by combining Eqs. (1) and (2):

              (5)

Since Eq. (5) is an implicit system of equations, it needs to be calculated by iterative implicit step-by-step integration algorithm [46] or by explicit integration algorithm [47]. In this study, Wilson-θ was used for iterative calculation, and the convergence method was used for judgment [48].

3 Measures on track surface

In the analysis of RSPT on bridge during earthquake, in addition to the train-bridge coupling dynamic effect [49, 50], GM is transmitted from the bedrock to the pier bottom and then mapped from the pier bottom to the track surface, as shown in Figure 4. The dynamic response of the track surface, which is in directly contact with the wheelset, will directly affect RSPT. In order to provide a convenient seismic evaluation measure based on the RSPT for general simply supported bridges, the optimal measures will be selected from the track surface response.

Figure 4 Ground acceleration mapped to track surface

Generally, the GM intensity measure can be used to evaluate the strength of the GM withstanding the structure. For example, the optimal measure was selected by evaluating the correlation between the GM intensity measure and the structure response to analyze the seismic fragility of the bridge [51]. For the RSPT analysis during the earthquake, peak ground acceleration (PGA) was used [17, 52]. The RSPT on the bridge during earthquake was evaluated by the PV and VSI on the track surface, and some design guidelines have been proposed [34, 35].

As shown in Figure 4, in this study, the track surface response was used to measure the RSPT on the HSR bridges during the earthquake. Using GM intensity measures for reference, 15 commonly used GM intensity measures were selected, as listed in Table 1, and the specific literature calculation method was used [53]. The renamed track surface response measures are listed in Table 2. The main idea of this method is adjusting the GM intensity, and inputting the GM samples into the system. When the GM intensity just reaches the corresponding GM intensity of the train derailment limit state, the corresponding track acceleration time history response is recorded, and the new “GM” (Track response measures) can be used to calculate the corresponding measures. One of the advantages of this method is that it can focus on the response of the track surface, without paying too much attention to the structure under the rail, including the track-slab type and the non-linear of the bridge structure.

Table 1 GM intensity measures

Table 2 Track response measures

When analyzing the RSPT and bridge response during earthquakes, selecting random GM samples is necessary. The impact of different GM samples on structures and trains may be very different. In order to avoid obtaining results with tropism, the cloud chart method [54] was used to select 108 GM samples from the PEER website [55]. In this method, the epicenter distance and magnitude are each divided into two regions: a total of four regions, and the selected GM samples are evenly distributed in four regions in order to consider the randomness of seismic samples. Since near fault earthquakes were not considered in this study, the epicentral distance was considered in the range of 10-60 km, which is divided into two regions 10- 30 km and 30-60 km. The magnitude of the earthquake was in the range of 5.0-8.0, which was divided into 5.0-6.5 and 6.5-8.0. In the PEER website, 27 seismic samples were randomly selected from each region according to the input filtering conditions. The selection result is shown Figure 5. It can be seen that the selected samples are evenly distributed in the four blocks, and the randomness of the samples can be fully considered.

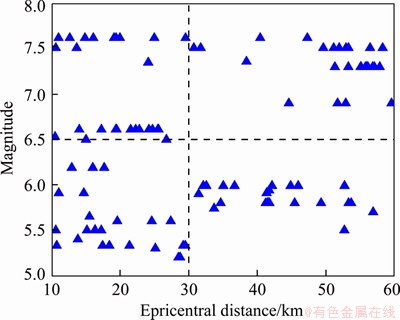
Figure 5 Cloud chart method for selection of GM samples

4 Measure evaluation

In order to obtain the threshold value of the track surface response measure for the RSPT on the bridge during the earthquake, the dichotomy method can be used to approximate the amplitude of the GM sample when the train reaches the derailment limit, as shown in Figure 6. The calculation indicates that a sufficiently accurate solution can be obtained through 8 times dichotomy method. Input each GM sample into the model of the train-bridge system under earthquake, adjust the amplitude of the GM acceleration, and record the track response of the GM sample under the acceleration amplitude, and then obtain the corresponding measure values through calculation.

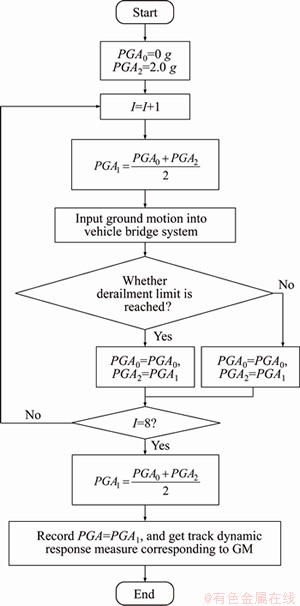
Figure 6 Dichotomy method to obtain driving safety limit calculation

The coupling vibration of the train-bridge is more complicated to simulate the actual derailment of train. Usually, some evaluation indexes can be used to determine whether the train is derailed, such as derailment coefficient, wheel load reduction rate and wheel-rail relative displacement [50, 56]. Derailment coefficient is the most commonly used evaluation index [16, 23, 45]. In this study, the derailment coefficient was used to judge the derailment limit. According to the Chinese code [57], the derailment coefficient is defined as 0.8, the limit value of RSPT, and it is calculated by Eq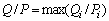. (6):

                        (6)

where Q and P denote the lateral and vertical force of wheel-rail, respectively; and the subscript i denotes the i-th wheelset.

The COV was used for evaluating the optimal measures from the 16 track surface response measures. In probability theory and statistics, COV is a normalized measure of the dispersion of probability distribution and is defined as the ratio of standard deviation to mean value, which can be written as:

                             (7)

where s and m are the standard deviation and mean value of sample value, respectively.

The smaller the COV, the smaller the dispersion of the results and the better the measurement method. In the calculation, the lateral period of the bridge from 0.1 to 1.9 s was considered, and this range of natural vibration period basically covers all situations of the simply supported bridge structure of the HSR. The train speeds were considered to be in the range from 100 to 400 km/h with an interval 50 km/h. In each working condition, the same track irregularities (converted from China’s HSR spectrum [58]) were applied in calculation. The train used the Chinese HSR EMU CRH2. The parameters of CRH2 are shown in Table 3, where m and I denote the mass and moment of inertia, respectively, and other symbols can be found in Figure 1.

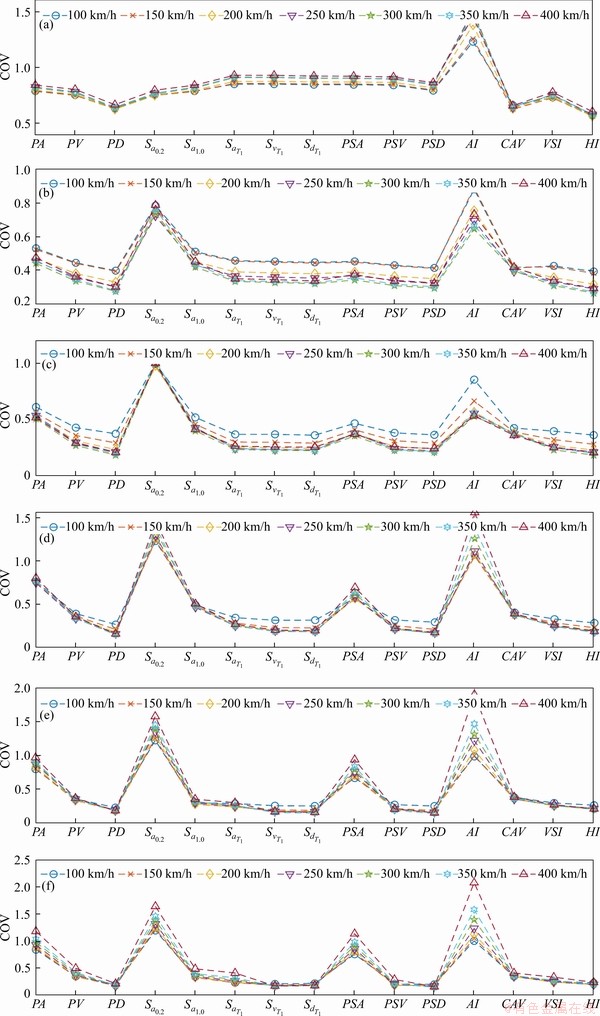
The 108 GM samples were sequentially input into the train-bridge system with different train speeds and different structural periods to obtain the limit values of each track surface measures, and they were sorted to obtain the corresponding COV, as shown in Figure 7. The COV is a measure used to evaluate the sample dispersion, and the larger the COV, the greater the discreteness of samples. The COV of a certain measure is different at different speeds, and with increasing structural period, the variation is more obvious and will increase with increasing train speed, indicating that the discreteness of the measure limit varies with the speed of the train, and will increase with increasing speed. In addition, the COVs of most measures are greater than 0.25, and many of them are greater than 0.5, or even more than 1.0, indicating that the dispersion of most measure limits is large.

Table 3 Parameters of CRH2

During different bridge structure periods, the COV of each measure limit is also different. For example, in the interval from 0.1 to 0.5 s, the COV of HI is the smallest; but when the period of the structure is larger than 0.5 s, the COV gradually increases. Among the types of response spectrum measures, except for PSA, the variability of other measure limits decreases with increasing structural period. Among them, S_vT1 and PSD have smaller variability in medium and long-period bridge structures. Therefore, the advantages of different evaluation measures are different under different natural vibration periods.

The smaller the COV, the smaller the discreteness of the sample, indicating the superiority of the measure. In order to more intuitively show the superiority of each measure in different structural periods, the method of ranking the measure superiority by sorting the COV from small was adopted. The result is shown in Figure 8. The HI and PD have a higher occurrence rate in the first four structural periods. In the period of 0.1- 0.5 s, the HI is the optimum, followed by PD; in the periods of 0.7 s and 1.3-1.9 s, PD has the best advantage, whereas in the period of 0.9-1.1 s, PSD has the best advantage.

It is suggested that HI should be used in the period range from 0.1 to 0.5 s; for the case of 0.5 s period, PSD ranks the fourth in the superiority; for the case of 0.7 s period, although the COV of PD is smaller than that of PSD, the two are very close. For the case of structural period of 1.3 s, PSD has the second advantage. Therefore, from the perspective of continuity, PSD is recommended to be used as measure in the range of 0.5-1.3 s period; PD is recommended as a measure when the structural period is more than 1.3 s. The details are as follows:

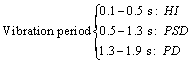             (8)

5 Measure limit

According to the discussion in Section 4, the minimum value of the track surface response threshold corresponding to different speeds and different structure natural vibration periods was calculated through 108 GM samples as the safety limit value of HSR train on the bridge during earthquake, as shown in Figure 9. Figure 9(a) shows the RSPT measure considering the period of 0.1-0.5 s. It can be seen that the limit measure HI decreases with the increase of speed. In addition,the measure limit value increases with increasing structural period.

to be continued

Continued

Figure 7 COV of each measure under different structure periods and different speeds:

Figure 8 Different structure periods corresponding to each measure superiority rank

Figure 9(b) shows the RSPT measure considering the period of 0.5-1.3 s. In this range, PSD is used as the measure. In addition, for different speeds, when the period of bridge structure is in the range of 0.5–1.1 s period, the PSD limit of measure increases with increasing period. When the period is larger than 1.1 s, the limit value will decrease with increasing period.

Figure 9(c) shows the RSPT measure considering the range of 1.3-1.9 s period, and in this range, PD is used as the measure. When the train speed is 100, 150 and 200 km/h, the measure limit is relatively close; and when the train speed is 300 and 350 km/h, the measure limit is relatively close. When the period of structure is larger than 1.7 s and the speed is smaller than 400 km/h, the measure limit is independent with train speed.

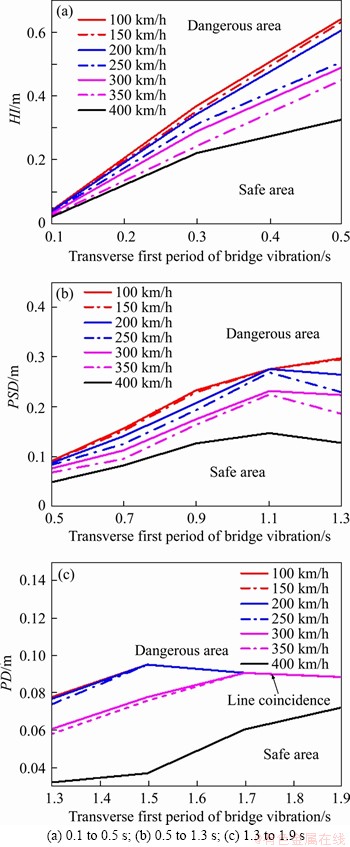
Figure 9 Track surface response measure limit based on RSPT:

6 Conclusions

In conclusion, based on the finite element theory, multi-rigid body dynamics and simplified wheel rail contact model, the calculation model of train running safety on bridge under earthquake was established in this study. The track surface response limits in the case of train derailment with different bridge structure natural vibration periods and train speed were calculated, leading to the variation coefficient of 15 track surface measures, in order to select the optimal measures. According to the optimal measures, the limit value of seismic response measures of bridge based on RSPT with different structural periods was calculated, and the results are as follows:

1) The discreteness of the limit value with different speeds is different, and the dispersion increases with increasing train speed, but the change trend of each measure is relatively close; most of the measure limits have large dispersion, and some even exceed 1.0, belonging to strong variation.

2) In the period of 0.1-0.5 s, the COV of HI is the smallest, but when the period of structure is larger than 0.5 s, the COV gradually increases; in spectrum type measure, except PSA, the variability of other measure limits decreases with increasing structural period, in which S_vT1 and PSD have small variability in medium and long-term bridge structures.

3) In the period of 0.1-0.5 s, the H/I is optimum; in the period from 0.5 to 1.3 s, PSD is the optimal; in the range of 1.3-1.9 s period, PD is the optimal measure.

4) The response measure HI in the range of 0.1–0.5 s period will increases with increasing structural period and decrease with increasing train speed.

5) PSD is suggested for response measure of RSPT within the range of 0.5-1.3 s period. For different speeds, when the period of bridge structure is in the range of 0.5–1.1 s period, the PSD limit of measure increases with increasing period. When the period is larger than 1.1 s, the limit value will decrease with increasing period.

6) PD is suggested for response measure of RSPT considering the range from 1.1 to 1.9 s.

Contributors

LIU Xiang written the manuscript and established the models. JIANG Li-zhong and XIANG Ping provided the concept and idea. LAI Zhi-peng established the models and calculated the results. FENG Yu-lin and CAO Shan-shan analyzed the data.

Conflict of interest

LIU Xiang, JIANG Li-zhong, XIANG Ping, LAI Zhi-peng, FENG Yu-lin and CAO Shan-shan declare that they have no conflict of interest.

References

[1] KANG Chong-jie, SCHNEIDER S, WENNER M, MARX S. Experimental investigation on the fatigue behaviour of rails in the transverse direction [J]. Construction and Building Materials, 2021, 272: 121666. DOI: 10.1016/j.conbuildmat. 2020.121666.

[2] KANG Chong-jie, BODE M, WENNER M, MARX S. Experimental and numerical investigations of rail behaviour under compressive force on ballastless track systems [J]. Engineering Structures, 2019, 197: 109413. DOI: 10.1016/ j.engstruct.2019.109413.

[3] KANG Chong-jie, SCHNEIDER S, WENNER M, MARX S. Experimental investigation on rail fatigue resistance of track/bridge interaction [J]. Engineering Structures, 2020, 216: 110747. DOI: 10.1016/j.engstruct.2020.110747.

[4] FENG Y, JIANG L, ZHOU W, LAI Z, CHAI X. An analytical solution to the mapping relationship between bridge structures vertical deformation and rail deformation of high-speed railway [J]. Steel and Composite Structures, 2019, 33: 209–224. DOI: 10.12989/scs.2019.33.2.209

[5] SU Miao, DAI Gong-lian, PENG Hui. Bond-slip constitutive model of concrete to cement-asphalt mortar interface for slab track structure [J]. Structural Engineering and Mechanics, 2020, 74: 589–600. DOI: 10.12989/sem.2020.74.5.589.

[6] LAI Zhi-peng, JIANG Li-zhong, LIU Xiang, ZHANG Yun-tai, ZHOU Wang-bao. Analytical investigation on the geometry of longitudinal continuous track in high-speed rail corresponding to lateral bridge deformation [J]. Construction and Building Materials, 2021, 268: 121064. DOI: 10.1016/ j.conbuildmat.2020.121064.

[7] JIANG Li-zhong, FENG Yu-lin, ZHOU Wang-bao, HE Bin-bin. Vibration characteristic analysis of high-speed railway simply supported beam bridge-track structure system [J]. Steel and Composite Structures, 2019, 31(6): 591-600. DOI: 10.12989/scs.2019.31.6.591.

[8] LAI Zhi-peng, JIANG Li-zhong, ZHOU Wang-bao. An analytical study on dynamic response of multiple simply supported beam system subjected to moving loads [J]. Shock and Vibration, 2018: 1-14. DOI: 10.1155/ 2018/2149251.

[9] LAI Zhi-peng, KANG Xin, JIANG Li-zhong, ZHOU Wang-bao, FENG Yu-lin, ZHANG Yun-tai, YU Jian, NIE Lei-xin. Earthquake influence on the rail irregularity on high-speed railway bridge [J]. Shock and Vibration, 2020: 1-16. DOI: 10.1155/2020/4315304.

[10] ZHU Y, WEI Y. Characteristics of railway damage due to wenchuan earthquake and countermeasure considerations of engineering seismic design [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29: 3378–3386. (in Chinese)

[11] ZENG Qing, DIMITRAKOPOULOS E G. Vehicle-bridge interaction analysis modeling derailment during earthquakes [J]. Nonlinear Dynamics, 2018, 93(4): 2315-2337. DOI: 10.1007/s11071-018-4327-6.

[12] GB50111-2006. Code for seismic design of railway engineering [S]. (in Chinese)

[13] GB50909-2014. Code for seismic design of urban rail transit structures [S]. (in Chinese)

[14] JU S H. A simple finite element for nonlinear wheel/rail contact and separation simulations [J]. Journal of Vibration and Control, 2014, 20(3): 330-338. DOI: 10.1177/ 1077546312463753.

[15] JU S H, HUNG S J. Derailment of a train moving on bridge during earthquake considering soil liquefaction [J]. Soil Dynamics and Earthquake Engineering, 2019, 123: 185-192. DOI: 10.1016/j.soildyn.2019.04.019.

[16] JU S H. Nonlinear analysis of high-speed trains moving on bridges during earthquakes [J]. Nonlinear Dynamics, 2012, 69(1, 2): 173-183. DOI: 10.1007/s11071-011-0254-5.

[17] YAU J D. Dynamic response analysis of suspended beams subjected to moving vehicles and multiple support excitations [J]. Journal of Sound and Vibration, 2009, 325(4, 5): 907-922. DOI: 10.1016/j.jsv.2009.04.013.

[18] YANG Y B, WU Y S. Dynamic stability of trains moving over bridges Shaken by earthquakes [J]. Journal of Sound and Vibration, 2002, 258(1): 65-94. DOI: 10.1006/ jsvi.2002.5089.

[19] MONTENEGRO P A, CALCADA R, VILA POUCA N, TANABE M. Running safety assessment of trains moving over bridges subjected to moderate earthquakes [J]. Earthquake Engineering & Structural Dynamics, 2016, 45(3): 483-504. DOI: 10.1002/eqe.2673.

[20] ZENG Zhi-ping, ZHAO Yan-gang, XU Wen-tao, YU Zhi-wu, CHEN Ling-kun, LOU Ping. Random vibration analysis of train-bridge under track irregularities and traveling seismic waves using train-slab track-bridge interaction model [J]. Journal of Sound and Vibration, 2015, 342: 22-43. DOI: 10.1016/j.jsv.2015.01.004.

[21] XU Lei, ZHAI Wan-ming. Stochastic analysis model for vehicle-track coupled systems subject to earthquakes and track random irregularities [J]. Journal of Sound and Vibration, 2017, 407: 209-225. DOI: 10.1016/j.jsv.2017. 06.030.

[22] ZHANG Z C, LIN J H, ZHANG Y H, ZHAO Y, HOWSON W P, WILLIAMS F W. Non-stationary random vibration analysis for train-bridge systems subjected to horizontal earthquakes [J]. Engineering Structures, 2010, 32(11): 3571-3582. DOI: 10.1016/j.engstruct.2010.08.001.

[23] DU X T, XU Y L, XIA H. Dynamic interaction of bridge-train system under non-uniform seismic ground motion [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(1): 139-157. DOI: 10.1002/eqe.1122.

[24] JIN Zhi-bin, PEI Shi-ling, LI Xiao-zhen, LIU Hong-yan, QIANG Shi-zhong. Effect of vertical ground motion on earthquake-induced derailment of railway vehicles over simply-supported bridges [J]. Journal of Sound and Vibration, 2016, 383: 277-294. DOI: 10.1016/j.jsv.2016.06.048.

[25] ZHU Zhi-hui, GONG Wei, WANG Kun, LIU Yu, DAVIDSON M T, JIANG Li-zhong. Dynamic effect of heavy-haul train on seismic response of railway cable-stayed bridge [J]. Journal of Central South University, 2020, 27(7): 1939-1955. DOI: 10.1007/s11771-020-4421-z.

[26] JIANG Li-zhong, YU Jian, ZHOU Wang-bao, YAN Wang-ji, LAI Zhi-peng, FENG Yu-lin. Applicability analysis of high-speed railway system under the action of near-fault ground motion [J]. Soil Dynamics and Earthquake Engineering, 2020, 139: 106289. DOI: 10.1016/j.soildyn. 2020.106289.

[27] YU Jian, JIANG Li-zhong, ZHOU Wang-bao, LIU Xiang, LAI Zhi-peng, FENG Yu-lin. Study on the dynamic response correction factor of a coupled high-speed train-track-bridge system under near-fault earthquakes [J]. Mechanics Based Design of Structures and Machines, 2020: 1-19. DOI: 10.1080/15397734.2020.1803753.

[28] NISHIMURA K, TERUMICHI Y, MORIMURA T, SOGABE K. Development of vehicle dynamics simulation for safety analyses of rail vehicles on excited tracks [J]. Journal of Computational and Nonlinear Dynamics, 2009, 4(1): 011001. DOI: 10.1115/1.3007901.

[29] TANABE M, MATSUMOTO N, WAKUI H, SOGABE M, OKUDA H, TANABE Y. An efficient numerical method for dynamic interaction analysis of shinkansen train and railway structure during an earthquake [C]// Proceedings of ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Las Vegas, Nevada, USA, 2009: 1837-1845. DOI: 10.1115/DETC2007-34475.

[30] MIYAMOTO T, ISHIDA H. Numerical analysis focusing on the running safety of an improved bogie during seismic vibration [J]. Quarterly Report of RTRI, 2008, 49(3): 173-177. DOI: 10.2219/rtriqr.49.173.

[31] MATSUMOTO N, OKANO M, OKUDA H, WAKUI H, OHUCHI H. New railway viaduct providing superior running safety at earthquake [C]// IABSE Congress, Lucerne 2000: Structural Engineering for Meeting Urban Transportation Challenges. Zurich, Switzerland: International Association for Bridge and Structural Engineering (IABSE), 2000: 315-322. DOI: 10.2749/222137900796298832.

[32] NISHIMURA K, TERUMICHI Y, MORIMURA T, ADACHI M, MORISHITA Y, MIWA M. Using full scale experiments to verify a simulation used to analyze the safety of rail vehicles during large earthquakes [J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(3): 031013. DOI: 10.1115/1.4027756.

[33] WEI Feng, ZHANG Zhi-fang, GAO Liang. Study on shaking table array test of HSR train-track-bridge system under seismic action and velocity threshold of earthquake early warning [J]. Journal of the China Railway Society, 2018, 40(3): 101-106. (in Chinese)

[34] LUO Xiu. Study on methodology for running safety assessment of trains in seismic design of railway structures [J]. Soil Dynamics and Earthquake Engineering, 2005, 25(2): 79-91. DOI: 10.1016/j.soildyn.2004.10.005.

[35] LUO Xiu, MIYAMOTO T. Method for running safety assessment of railway vehicles against structural vibration displacement during earthquakes [J]. Quarterly Report of RTRI, 2007, 48(3): 129-135. DOI: 10.2219/rtriqr.48.129.

[36] LIU Xiang, JIANG Li-zhong, LAI Zhi-peng, XIANG Ping, CHEN Yuan-jun. Sensitivity and dynamic analysis of train-bridge coupled system with multiple random factors [J]. Engineering Structures, 2020, 221: 111083. DOI: 10.1016/ j.engstruct.2020.111083.

[37] JIANG Li-zhong, LIU Xiang, XIANG Ping, ZHOU Wang-bao. Train-bridge system dynamics analysis with uncertain parameters based on new point estimate method [J]. Engineering Structures, 2019, 199: 109454. DOI: 10.1016/ j.engstruct.2019.109454.

[38] LIU Xiang, XIANG Ping, JIANG Li-zhong, LAI Zhi-peng, ZHOU Tuo, CHEN Yuan-jun. Stochastic analysis of train–bridge system using the karhunen–loéve expansion and the point estimate method [J]. International Journal of Structural Stability and Dynamics, 2020, 20(2): 2050025. DOI: 10.1142/s021945542050025x.

[39] XU Lei, XIN Li-feng, YU Zhi-wu, ZHU Zhi-hui. Construction of a dynamic model for the interaction between the versatile tracks and a vehicle [J]. Engineering Structures, 2020, 206: 110067. DOI: 10.1016/j.engstruct.2019.110067.

[40] XIN Li-feng, LI Xiao-zhen, ZHU Yan, LIU Ming. Uncertainty and sensitivity analysis for train-ballasted track-bridge system [J]. Vehicle System Dynamics, 2020, 58(3): 453-471. DOI: 10.1080/00423114.2019.1584678.

[41] JIANG Li-zhong, LIU Xiang, ZHOU Tuo, XIANG Ping, CHEN Yuan-jun, FENG Yu-lin, LAI Zhi-peng, CAO Shan-shan. Application of KLE-PEM for random dynamic analysis of nonlinear train-track-bridge system [J]. Shock and Vibration, 2020: 1-10. DOI: 10.1155/2020/ 8886737.

[42] ZENG Q, GUO X. Theory and application of vibration analysis of train-bridge time-dependent system [M]. Beijing: China Railway Publishing House,1999. (in Chinese)

[43] CAO Shan-shan, JIANG Li-zhong, WEI Biao. Numerical and experimental investigations on the Park-Ang damage index for high-speed railway bridge piers with flexure failures [J]. Engineering Structures, 2019, 201: 109851. DOI: 10.1016/j.engstruct.2019.109851.

[44] MUNOZ S, ACEITUNO J F, URDA P, ESCALONA J L. Multibody model of railway vehicles with weakly coupled vertical and lateral dynamics [J]. Mechanical Systems and Signal Processing, 2019, 115: 570-592. DOI: 10.1016/ j.ymssp.2018.06.019.

[45] CHENG Y C, CHEN C H, HSU C T. Derailment and dynamic analysis of tilting railway vehicles moving over irregular tracks under environment forces [J]. International Journal of Structural Stability and Dynamics, 2017, 17(9): 1750098. DOI: 10.1142/s0219455417500985.

[46] ZHANG Nan, XIA He. Dynamic analysis of coupled vehicle-bridge system based on inter-system iteration method [J]. Computers & Structures, 2013, 114-115: 26-34. DOI: 10.1016/j.compstruc.2012.10.007.

[47] ZHAI Wan-ming, XIA He, CAI Cheng-biao, GAO Mang-mang, LI Xiao-zhen, GUO Xiang-rong, ZHANG Nan, WANG Kai-yun. High-speed train-track-bridge dynamic interactions–Part I: Theoretical model and numerical simulation [J]. International Journal of Rail Transportation, 2013, 1(1, 2): 3-24. DOI: 10.1080/23248378.2013.791498.

[48] LEI X, NODA N A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile [J]. Journal of Sound and Vibration, 2002, 258(1): 147-165. DOI: 10.1006/jsvi.2002.5107.

[49] CHEN Zhao-wei, ZHAI Wan-ming. Theoretical method of determining pier settlement limit value for China's high-speed railway bridges considering complete factors [J]. Engineering Structures, 2020, 209: 109998. DOI: 10.1016/ j.engstruct.2019.109998.

[50] CHEN Zhao-wei, ZHAI Wan-ming, TIAN Guo-ying. Study on the safe value of multi-pier settlement for simply supported girder bridges in high-speed railways [J]. Structure and Infrastructure Engineering, 2018, 14(3): 400-410. DOI: 10.1080/15732479.2017.1359189.

[51] WEI Biao, HU Zhang-liang, HE Xu-hui, JIANG Li-zhong. Evaluation of optimal ground motion intensity measures and seismic fragility analysis of a multi-pylon cable-stayed bridge with super-high piers in Mountainous Areas [J]. Soil Dynamics and Earthquake Engineering, 2020, 129: 105945. DOI: 10.1016/j.soildyn.2019.105945.

[52] XIA He, HAN Yan, ZHANG Nan, GUO Wei-wei. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations [J]. Earthquake Engineering & Structural Dynamics, 2006, 35(12): 1563-1579. DOI: 10.1002/eqe.594.

[53] GUO Jun-jun, ALAM M S, WANG Jing-quan, LI Shuai, YUAN Wan-cheng. Optimal intensity measures for probabilistic seismic demand models of a cable-stayed bridge based on generalized linear regression models [J]. Soil Dynamics and Earthquake Engineering, 2020, 131: 106024. DOI: 10.1016/j.soildyn.2019.106024.

[54] TONDINI N, STOJADINOVIC B. Probabilistic seismic demand model for curved reinforced concrete bridges [J]. Bulletin of Earthquake Engineering, 2012, 10(5): 1455-1479. DOI: 10.1007/s10518-012-9362-y.

[55] PEER (Pacific Earthquake Engineering Research Center). Ground motion database [EB/OL][2019]. http://ngawest2. berkeley.edu.

[56] GOU Hong-ye, YANG Long-cheng, MO Zhi-xiang, GUO Wei, SHI Xiao-yu, BAO Yi. Effect of long-term bridge deformations on safe operation of high-speed railway and vibration of vehicle–bridge coupled system [J]. International Journal of Structural Stability and Dynamics, 2019, 19(9): 1950111. DOI: 10.1142/s0219455419501116.

[57] ZHAI Wan-ming, XIA He. Train-track-bridge dynamic interaction: theory and engineering application [M]. Beijing: Science Press, 2011. (in Chinese)

[58] ZHAI Wan-ming, LIU Peng-fei, LIN Jian-hui, WANG Kai-yun. Experimental investigation on vibration behaviour of a CRH train at speed of 350 km/h [J]. International Journal of Rail Transportation, 2015, 3(1): 1-16. DOI: 10.1080/23248378.2014.992819.

(Edited by ZHENG Yu-tong)

中文导读

考虑列车行车安全性能的地震下高速铁路桥梁动力响应限值

摘要：由于我国铁路网广、地震带多等特点，在高速铁路桥梁结构设计中，考虑列车运行安全性能是十分必要的。为了提供基于桥上高速列车行车安全性能的桥梁结构抗震设计和评估方法，本文建立了地震作用下桥上高速列车行车安全的计算模型，参考15种常用的地震动强度指标计算脱轨系数达到极限值时的轨面响应指标。根据多个地震动样本得到指标极限值的变异系数，并选择最优指标。最后，根据所选的最优指标确定了不同列车速度、不同结构周期下基于列车行车安全性能的桥梁地震响应指标极限值。

关键词：高速铁路桥梁；抗震设计；行车安全；指标限值

Foundation item: Projects(U1934207, 51778630, 11972379) supported by the National Natural Science Foundation of China; Project(2020zzts148) supported by the Fundamental Research Funds for the Central Universities, China; Project(GJJ200657) supported the Research Project of Jiangxi Provincial Education Department, China

Received date: 2020-08-20; Accepted date: 2021-01-13

Corresponding author: LAI Zhi-peng, PhD; Tel: +86-18975158579; E-mail: zhplai@csu.edu.cn; ORCID: https://orcid.org/0000-0003- 4569-8345