基于数据截断和变间隔插值的空间脉动风场模拟
郭文华1, 2,项超群1,张佳文1
(1.中南大学 土木工程学院,湖南 长沙,410004;
2.中南大学 高速铁路建造技术国家工程实验室,湖南 长沙,410004)
摘要:对大跨度桥梁空间脉动风场模拟提出一种改进的谐波合成法。研究分解谱函数随频率的变化规律,确定分解谱函数矩阵不同位置元素对应的有效截止频率。对互谱矩阵的Cholesky分解仅需在插值节点频率进行,而对于其他频率点的分解谱函数则采用三次拉格朗日插值拟合,并探讨不同插值节点间隔对拟合精度的影响。根据谐波合成法中相关矩阵的特点,仅对下三角部分采用一维存储,以节省存储空间。综合考虑计算效率和拟合精度,提出变间隔插值算法。对某一大跨度斜拉桥进行空间脉动风场的模拟。研究结果表明:随着频率增大,分解谱函数矩阵非对角线元素超过峰值后迅速单调趋近于0,即当频率超过其对应的有效截止频率后,分解谱函数对风速的贡献可忽略,据此即可对计算过程进行合理截断;分解谱函数在低频部分线形变化显著,宜采用较小的插值节点间隔,而在高频部分线形比较平缓,可采用较大的插值节点间隔。通过检验风速样本的功率谱密度函数和相关函数,验证了改进谐波合成法的正确性、高效性和可靠性。
关键词:空间脉动风场;改进谐波合成法;变间隔插值;数据截断;一维存储
中图分类号:U448.27 文献标志码:A 文章编号:1672-7207(2013)08-3326-09
Simulation of spatial fluctuating wind field based on truncation and variable intervals interpolation
GUO Wenhua1, 2, XIANG Chaoqun1, ZHANG Jiawen1
(1. School of Civil Engineering, Central South University, Changsha 410004, China;
2. National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410004, China)
Abstract: The improved wave superposition method for simulating spatial fluctuating wind field of long-span bridges was presented. The variation tendency of factorized spectral function with frequency was investigated, the maximum effective frequency of every element of factorized spectral function matrix was determined. Cross spectral matrix was factorized with Cholesky algorithm only on one part of interpolation nodes’ frequencies, and factorized spectral function on other frequencies fitted with Cubic Lagrange interpolation according to the computed values on interpolation nodes’ frequencies, and the effects of different intervals of interpolation points on the fitting precision were studied. According to the characteristics of the matrix of wave superposition method, only the lower triangular part was stored with one-dimensional storage to save a large number of memory space. In comprehensive consideration of the calculation efficiency and fitting precision, variable intervals interpolation algorithm was proposed. Finally, the spatial fluctuating wind field of a long-span cable-stayed bridge was simulated. The results show that non-diagonal element of factorized spectral function matrix monotonously decrease to 0 with the increase of frequency after exceeding its peak, and its contribution to wind velocity can be neglected when the frequency exceeds the maximum effective frequency, therefore, the calculation is truncated properly. The denser interpolation points in low frequency section should be adopted for the curve of the factorized spectral function changed sharply and sparser interpolation points in high frequency section should be used for smoother curve. The improved wave superposition method proves to be, efficient and reliable by verifying the power spectral density function and correlation function of wind velocity sample.
Key words: spatial fluctuating wind field; improved wave superposition method; variable intervals interpolation; truncation; one-dimensional storage
为了分析大跨度桥梁结构在自然风作用下的随机振动,首先需得到作用于桥梁上的脉动风速时程。由于现场实测多点脉动风速非常困难,因此,常采用计算机模拟。大多数国内外学者将脉动风速视作平稳高斯随机过程,尽管目前模拟方法很多,但谐波合成法简单明了,精度较高,适应于任意谱特征,因而在脉动风速模拟中得到广泛采用[1]。Rice[2]提出了谐波合成法的基本概念。Shinozuka等[3-4]将谐波合成法用于模拟一个单变量的一维平稳随机过程,而后直接推广到n维单变量均匀随机场的模拟[5]。为了减少谐波叠加的计算量,Yang[6-7]将FFT技术应用于样本的模拟过程中,极大地提高了脉动风场的合成效率,此后,Shinozuka[8]又将FFT算法扩展到多维情况。由于谐波合成法将脉动风速时程看作一系列简谐波的叠加,因此,其为周期函数。但自然界的脉动风速实际上是没有周期的,为了使模拟样本尽可能与实际一致,Shinozuka引入“双索引”频率的概念以增大样本周期,但当时其模拟的样本函数不符合各态历经性假设,Deodatis[9]利用Shinozuka引入的“双索引”频率概念修正了平稳多变量随机过程的模拟方法,实现了样本函数的各态历经性模拟,并证明了模拟时长为1个周期时样本的均值和相关函数与目标值一致。然而,双索引频率的引入大大增加了离散频率点数,也大大增加了互谱矩阵Cholesky分解计算量。曹映泓等[10]推导了对互谱密度矩阵分解的显示表达式,但显示分解法要求模拟点高度相同、纵向间距相等,无法考虑桥塔或高墩处脉动风速的模拟。李永乐等[11]将面状的三维脉动风场简化为多个线状的一维脉动风场,采用互谱矩阵分解的显示表达式进行了斜拉桥主梁的脉动风场模拟,采用传统谐波合成法进行桥塔的风场模拟。丁泉顺等[12]通过对谱分解矩阵引入三次拉格朗日插值近似,从而提高谐波合成法的计算效率。包龙生等[13]采用BP神经网络来拟合分解谱密度函数曲线。李锦华等[14]使用样条插值技术来减少互谱矩阵的分解次数。罗俊杰等[15]分析了S(ω)经过分解后的矩阵H(ω)的特点,采用三次均匀B样条插值来拟合分解谱密度函数曲线。随着桥梁跨径不断增大,高墩高塔大量涌现,空间脉动风场模拟点数必然增加,传统谐波合成法分解计算量更大,从而将极大地影响计算效率。采用插值法能减少互谱密度矩阵分解的次数,加快计算速度,但以往的研究忽略了不同频率段对脉动风速的实际贡献,故一般在全部频率范围内选取插值节点进行互谱矩阵的Cholesky分解,分解谱函数在其他频率点上的值则通过插值得到。为此,本文作者研究分解谱函数矩阵随频率变化规律,得到其不同位置元素对应的有效截止频率。对分解谱函数采用三次拉格朗日插值,讨论不同插值节点间隔对其拟合精度的影响,进而提出针对分解谱函数矩阵中的不同元素仅在其有效截止频率内按变间隔选取插值节点进行互谱矩阵的Cholesky分解,以提高计算效率。
1 谐波合成法的基本过程
脉动风场实为多维多变量的零均值平稳高斯随机过程,但由于理论的不成熟且缺乏可靠的观测数据,各维度之间脉动分量的相关性难以考虑,故通常将其简化为一维n变量零均值平稳高斯随机过程,其双边互谱密度矩阵为
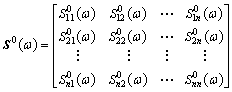
按照Cholesky分解法,互谱密度矩阵S0(ω)可以分解为
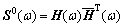
其中: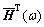 为H(ω)的共轭转置矩阵。对目标谱密度矩阵进行分解以后,根据Deodatis[9]理论,随机过程{f0(t)}的样本{f(t)}可以模拟为
为H(ω)的共轭转置矩阵。对目标谱密度矩阵进行分解以后,根据Deodatis[9]理论,随机过程{f0(t)}的样本{f(t)}可以模拟为
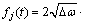
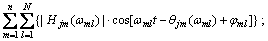
j=1,2,…,n
其中:θjm(ωml)为Hjm(ωml)的幅角。由于脉动风速的互相关函数是非对称的,既非偶函数,亦非奇函数,故空间不同点之间的脉动风互谱密度函数为复数。但在工程中常用实函数来表达,因而互谱密度矩阵S0(ω)为实对称矩阵,分解谱矩阵H(ω)为实数矩阵[12],其幅角θjm(ωml)为0。由于H(ω)矩阵为下三角矩阵,即当m>j时,Hjm(ωml)=0。而工程中给出的脉动风谱为单边谱,故式可以简化为
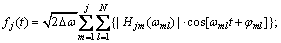
j=1,2,…,n
式中:N为上、下频率范围之间频率总段数,为一充分大的数,为利用FFT技术,一般设置为2的整数次幂;φml为均匀分布于(0,2π)区间的独立相位角。为增大模拟样本周期,Shinozuka引入了双索引频率[9],即
 l=1,2,…,N
l=1,2,…,N
功率谱密度频率区间为(0,ωu),共分为N段;频率增量为△ω=ωu/N。其中:ωu为截止频率,当ω>ωu时,S(ω)很小,可以忽略。
式为一系列简谐波的叠加,每个谐波分量的周期为
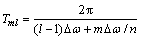
从而可知谐波分量的最大周期max(Tml)为
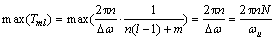
max(Tml)为单个谐波分量的整数倍,因而,谐波分量的最大周期即为样本周期。为避免模拟结果失真,根据采样定理,时间t的增量△t需满足△t≤π/ωu。
由于S(ωml)为Hermitian矩阵,H(ωml)为下三角矩阵,因此,都只需要下三角部分,故可采用一维存储形式,以节约空间和减少计算量。其主对角元地址为
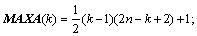
k=1,2,…,n
二维存储与一维存储的对应关系为
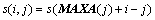
一维存储与二维存储的存储量比值为
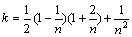
显然,n越大,节省效果越明显。谐波合成法风速合成过程包含2层循环,且要求N为一充分大的数,因此,该叠加过程很耗时。运用FFT技术可以大大减少风场模拟的计算量,从而提高计算效率。根据文献[9],将式改写为如下形式:
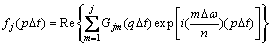
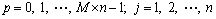
其中:q为p/M的余数。Gjm(q△t)可用FFT计算:
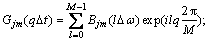
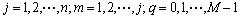
其中:
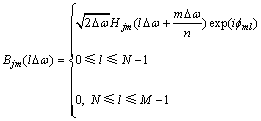
2 分解谱函数特征分析
谐波合成法的脉动风速由分解谱矩阵元素|Hjm(ω)|与含有随机成分的余弦之积叠加而成。由于|Hjm(ω)|是随频率变化的,故传统谐波合成法每一频率点都要进行互谱矩阵分解。在采用双索引频率后,频率点间隔为△ω/n,共有N×n个频率点,可见其计算量巨大。为了减少计算量,选取某大跨度桥梁,同时在主梁和桥塔上布置模拟点,根据《公路桥梁抗风设计指南》[16]分别对水平及竖向脉动风谱下分解谱函数随频率的变化规律进行分析。根据分解谱函数在矩阵中的位置,选取具有代表性的2组曲线,如图1和图2所示。
图1和图2所示仅给出了分解谱矩阵中4个元素随频率的变化规律曲线,其他同类型的分解谱函数元素变化规律与之相似。通过分析可知,水平风谱与竖向风谱的分解谱函数有共同的变化趋势。其规律如下。
(1) 对角线第1个元素随频率的增加而单调下降,最终将趋近于某一确定非零值。
(2) 对角线其他元素随频率的增加先上升,然后单调下降,最终将趋近于某一确定非零值。
(3) 非对角线第1列元素随频率的增加急剧下降,迅速稳定地趋近于0。
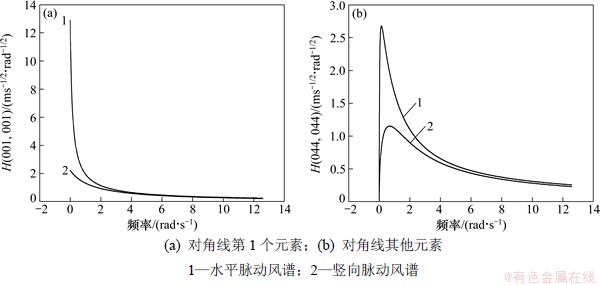
图1 分解谱矩阵对角线元素随频率的变化规律
Fig. 1 Variation tendencies of diagonal element of factorized spectral matrix with frequency
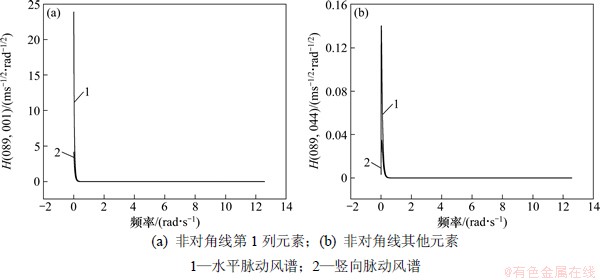
图2 分解谱矩阵非对角线元素随频率的变化规律
Fig. 2 Variation tendencies of non-diagonal element of factorized spectral matrix with frequency
(4) 非对角线其他元素随频率的增加在某一小频率范围内急剧上升,达到峰值之后迅速单调下降而趋近于0,峰值处于[0,1] rad/s内。
3 分解谱函数计算的截断
在谐波合成法中,当|Hjm(ω)|变小时,对风速的影响也变小。由上面的分析可知,非对角线第1列元素随频率的增加而单调减小并立即收敛至0,从而对脉动风速的贡献也单调减小至0。非对角线其他元素达到峰值后,将迅速趋近于0,从而对脉动风速的贡献也迅速趋近至0。由于分解谱矩阵非对角线元素过了峰值后(第1列元素无峰值)是单调非增函数,因此,当其小于某一足够小值时,可以忽略其后续频率点对叠加风速的影响。在此定义当某非对角线元素首次小于临界值时,所对应的频率即为该元素的有效截止频率ωe,当计算频率大于有效截止频率时不再对该元素进行计算,而直接赋值为0。现设临界值为1.0×10-7,对水平脉动风谱下分解谱矩阵元素首次小于该值的有效截止频率进行统计分析。算例中设有120个模拟点,截止频率为4π。分解谱函数矩阵仅存储下三角部分,共有元素7 260个。经过计算,共有6 961个元素在截止频率前达到临界值。将功率谱密度频率区间分成1 rad/s的频段,对每频段的有效截止频率出现次数进行统计,其随频率的分布规律如图3所示。
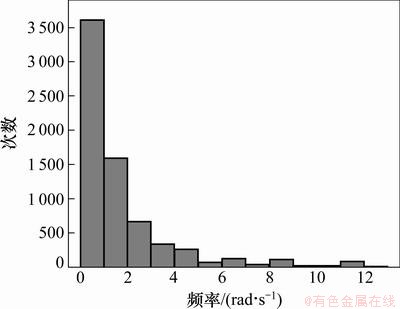
图3 有效截止频率分布直方图
Fig. 3 Histogram of the maximum effective frequency distribution
由于分解谱矩阵对角线元素最终趋近于非零值,因此,不能进行数据截断,即ωe=ωu。注意到分解谱矩阵不是第1列非对角线元素小频率时会先递增之后再递减,因此,对其有效截止频率的判别应进行双控,除了分解谱函数值外,还必须考虑当前频率范围。在研究中发现峰值都处于[0,1] rad/s,为了不至于在峰值之前将数据截断造成错误,本文在频率高于3.5 rad/s时再判断选取有效截止频率。
4 变间隔插值法拟合精度的分析
由于H(ω)的各元素均随频率连续变化,因此,可只对部分频率点的互谱矩阵采用Cholesky分解。设该部分频率点为插值节点,其余频率点的分解谱函数则通过插值得到。显然,插值节点布置越密,曲线拟合精度越高,但计算量也随之增大;相反,则计算量减少,但拟合精度下降。为了分析不同插值节点间隔对分解谱函数拟合精度的影响,本文选取某斜拉桥,采用《公路桥梁抗风设计指南》[16]的水平脉动风谱,用三次拉格朗日插值法计算了插值节点间隔分别为△ω,2△ω,3△ω,5△ω和10△ω的分解谱函数随频率变化曲线,并与全部频率点都采用Cholesky分解得到的分解谱函数曲线进行对比。在此选取分解谱矩阵对角线元素H(044,044)和非对角线元素H(044,014)在(0,1) rad/s区间的精度对比曲线,见图4和图5。
分解谱矩阵第1列元素为递减函数,由于不存在峰值而更加平滑,其插值拟合误差均很小;当频率高于0.5 rad/s时,采用不同插值节点间隔的分解谱函数曲线与目标曲线均较吻合,但在低频部分差别较大,故图4和图5中只给出了(0,1) rad/s的曲线。从图4和图5可知:当对角线元素插值节点间隔为2△ω时,与目标曲线较吻合;当非对角线元素插值节点间隔为2△ω时,与目标曲线相近,但峰值频率略往高频部分移动,当间隔为△ω时则与目标曲线较吻合。分解谱函数矩阵其他元素规律与上述同类型元素规律相同。为了兼顾插值精度和计算效率,可在曲线变化剧烈的频段布置较多的插值点,其余频段则可少布置插值点。鉴于观测到的规律,结合分解谱函数的数据截断,本文在 rad/s区间插值节点间隔采用△ω,在
rad/s区间插值节点间隔采用△ω,在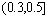 rad/s区间采用5△ω,在
rad/s区间采用5△ω,在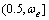 rad/s区间采用10△ω,高于ωe的频率区域不需再计算而直接赋值为0。经检验采用变间隔插值法的分解谱函数拟合精度较高,其中H(044,044)在(0,1) rad/s区间变间隔插值拟合结果如图6所示。
rad/s区间采用10△ω,高于ωe的频率区域不需再计算而直接赋值为0。经检验采用变间隔插值法的分解谱函数拟合精度较高,其中H(044,044)在(0,1) rad/s区间变间隔插值拟合结果如图6所示。
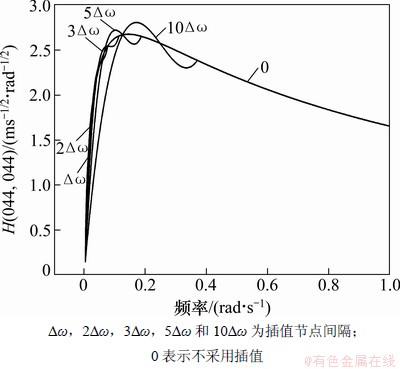
图4 分解谱矩阵对角线元素拟合精度对比
Fig. 4 Contrast of fitting precision of diagonal element in factorized spectral matrix

图5 分解谱矩阵非对角线元素拟合精度对比
Fig. 5 Fitting precision contrast of non-diagonal element of factorized spectral matrix
图6 变间隔插值分解谱函数与目标值对比
Fig. 6 Comparison between factorized spectral function of variable intervals interpolation and target
5 脉动风速模拟算例
为了验证分解谱函数采用数据截断和变间隔插值法的可靠性,本文选取某五跨斜拉桥为工程背景进行分析。该斜拉桥主跨为688 m,跨中离水面约66 m,桥塔高235 m,单个桥塔布置16个模拟点。斜拉索索面按扇形布置,主梁上标准索距为15 m,共设4×22对斜拉索,在拉索与主梁节点处均设置模拟点。全桥共布置模拟点120个。桥位处平均风剖面幂函数指数α=0.145,地面粗糙高度z0=0.001 m,基准风速v10=46.4 m/s,截止频率ωu=4π rad/s,频率分段数N=1 024,时间步长△t=0.25 s。桥型布置如图7所示。
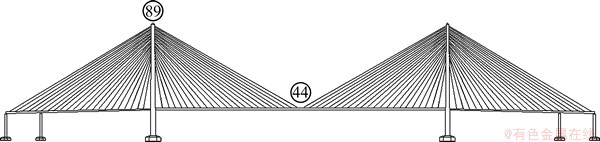
图7 斜拉桥桥型布置图
Fig. 7 Model of simulated cable-stayed bridge
由于该桥桥塔较高,风谱应考虑高度的影响,采用可以考虑风速随高度变化的Kaimal水平顺风向脉动风谱:
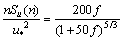
谐波合成法中用到的风谱是圆频率的形式,因此,将式转换成圆频率ω的形式可得[17]:
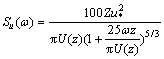
空间2点间的互功率谱密度由自谱密度函数,2点的空间相关系数共同决定。可以表示为[9]
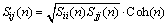
其中:Sii(n)和Sjj(n)分别为第i和j 2点的自谱密度函数;Coh(n)分别为i和j 2点的空间相关系数。在以往大跨度桥梁风振响应中,一般认为脉动风只作用于桥面,这不利于对桥梁整体抗风的精确分析[18],本文同时考虑了桥面和桥塔的脉动风速时程,空间相关系数采用Davenport的经验式[13, 19]:
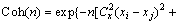
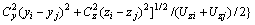
其中:cx,cy和cz为无量纲衰减系数,cx=16,cy=6,cz=10。
5.1 插值和截断对计算效率和误差的分析
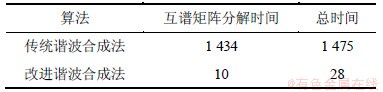
为了分析对互谱矩阵的分解过程引入插值和截断所产生的影响,从计算效率和截断误差2方面与传统的谐波合成法进行对比。由于数据截断只是作用在互谱矩阵的分解过程中,本文分别测试分解过程所用的时间,同时测试了模拟一组3 000 s样本所用的总时间,见表1。从表1可见:互谱矩阵分解所需时间缩短为传统谐波合成法的0.7%,样本模拟总时间缩短为原来的1.9%,由此可见本文采用的改进谐波合成法大大提高了计算效率。
变间隔插值法对分解谱函数的拟合具有很高的精度,如图6所示,因此,其对脉动风合成所产生的影响很小。本例中计算点数n=120,频率分段数N=1 024,取临界值10-7,判断起始频率ω′=3.5 rad/s,则对于某模拟点j,某时间步下的风速fj(t)由数据截断所产生的最大误差e为
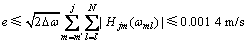
由于谐波合成法中每项|Hjm(ω)|均与一余弦项相乘再累加,因此,实际误差值小于式的计算误差,故对互谱密度矩阵只在插值节点进行分解和对分解谱函数采用三次拉格朗日插值和合理数据截断的加速算法对脉动风速的合成基本无影响。
表1 时间对比
Table 1 Time contrast s
5.2 功率谱与相关函数的检验
功率谱密度函数反映了空气紊流中各频率成分能量分布,相关函数反映了脉动风不同时刻的相关程度,它们是脉动风速场关键的特征参数。脉动风模拟的准则是模拟的风速场与目标风速场具有同样的特征,因此,应对模拟的脉动风速时程进行功率谱密度函数和相关函数的检验。Deodatis在文献[9]中证明了当样本时长为1个周期时,模拟值与目标值一致,因此,本文计算1个周期的样本用于检验功率谱和相关函数。
图8所示为主跨跨中44号点和左塔塔顶89号点的前2 000 s的脉动风速时程曲线。从图8可以看出:89号点因位置更高,其低频长周期成分更明显,符合空间脉动风的基本特征。
图9和图10所示分别为44号点和89号点功率谱密度函数检验和相关性检验结果。从图8和图9可见:功率谱密度函数和相关函数都和目标值较吻合。说明尽管本文对互谱密度矩阵的分解进行了截断和插值,减少了计算量,但所得的风速样本的精度基本不受影响,完全能满足工程需要。
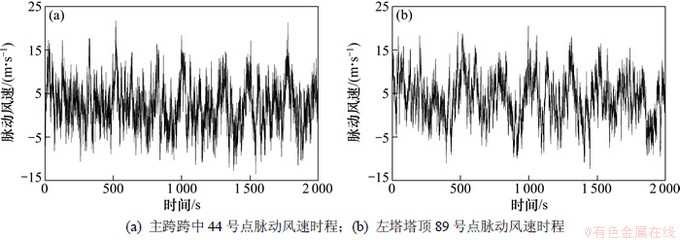
图8 模拟的脉动风速时程
Fig. 8 Time histories of simulated fluctuating wind velocity
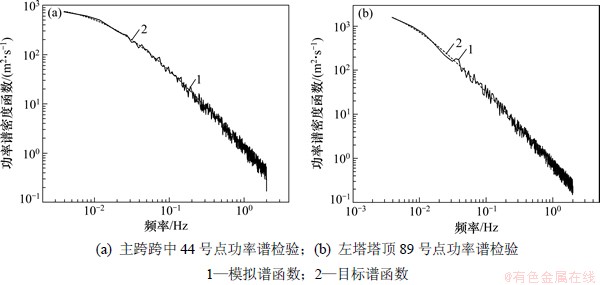
图9 功率谱密度函数检验
Fig. 9 Comparison of simulated and target PSD variances
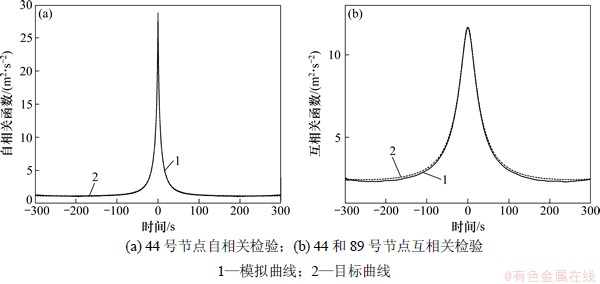
图10 相关性检验
Fig. 10 Comparison of simulated and target correlation variances
6 结论
(1) 针对谐波合成法存储数据多的缺陷,根据互谱密度矩阵和分解谱函数矩阵的特点,采用一维存储的方法,以节省存储空间。
(2) 随频率增加,分解谱矩阵对角线元素最终趋近于非零值;而非对角线第1列元素快速稳定趋近于0,非对角线其他元素达到峰值后再快速减小趋近于0。
(3) 随频率增加,分解谱矩阵非对角线元素对脉动风速的贡献快速降低,当计算频率大于该元素对应的有效截止频率时,可进行数据截断,即该元素不再计算而直接赋值为0。由于非对角线元素在小频率时可能存在1个峰值,故有效截止频率的判断应在峰值对应的频率之后进行。
(4) 对分解谱函数曲线采用三次拉格朗日插值,分解谱函数在低频部分曲线变化剧烈,宜采用较密的插值节点间隔;在高频部分曲线比较平缓,宜采用较稀的插值节点间隔。综合计算效率和拟合精度,提出了变间隔插值实施方法。
(5) 通过算例分析,验证了对分解谱函数同时采用数据截断和变间隔插值法对计算效率有很大提高。对模拟脉动风速样本进行了功率谱和相关函数检验,进一步验证了该方法的正确性和可靠性。
参考文献:
[1] Spanos P D, Zeldin B A. Monte Carlo treatment of random fields: a broad perspective[J]. Applied Mechanics Reviews, 1998, 51(3): 219-237.
[2] Rice S O. Mathematic analysis of random noise: Selected papers on noise and stochastic processes[M]. Wax N, eds. New York: Dover Publish Inc, 1954: 133-294.
[3] Shinozuka M,Deodatis G.Simulation of stochastic processes by spectral representation[J]. Applied Mechanics Reviews, 1991, 44(4): 191-204.
[4] Shinozuka M, Jan C M.Digital simulation of random processes and its applications[J]. Journal of Sound and Vibration, 1972, 25(1): 111-128.
[5] Deodatis G, Shinozuka M. Simulation of seismic ground motion using stochastic waves[J]. Journal of Engineering Mechanics, 1989, 115(12): 2723-2737.
[6] Yang J N. Simulation of random envelope processes[J]. Journal of Sound and Vibration, 1972, 25(1): 73-85.
[7] Yang J N. On the normality and accuracy of simulated random processes[J]. Journal of Sound and Vibration, 1973, 26(3): 417-428.
[8] Shinozuka M. Stochastic problems in mechanics: Digital simulation of random processes in engineering mechanics with the aid of FFT technique[M]. Waterloo: University of Waterloo Press, 1974: 277-286.
[9] Deodatis G. Simulation of ergodic multivariate stochastic process[J]. Journal of Engineering Mechanics, 1996, 122(8): 778-787.
[10] 曹映泓, 项海帆, 周颖. 大跨度桥梁随机风场的模拟[J]. 土木工程学报, 1998, 31(3): 72-79.
CAO Yinghong, XIANG Haifan, ZHOU Ying. Simulation of stochastic wind field on long-span bridge[J]. China Civil Engineering Journal, 1998, 31(3): 72-79.
[11] 李永乐, 周述华, 强士中. 大跨度斜拉桥三维脉动风场模拟[J]. 土木工程学报, 2003, 36(10): 60-65.
LI Yongle, ZHOU Shuhua, QIANG Shizhong. Simulation of three dimensional fluctuating wind field for large span cable-stayed bridge[J]. China Civil Engineering Journal, 2003, 36(10): 60-65.
[12] 丁泉顺, 陈艾荣, 项海帆. 大跨度桥梁空间脉动风场的计算机模拟[J]. 力学季刊, 2006, 27(2): 184-189.
DING Quanshun, CHEN Airong, XIANG Haifan. Simulation of spatial fluctuating wind field on long span bridges[J]. Chinese Quarterly of Mechanics, 2006, 27(2): 184-189.
[13] 包龙生, 刘克同, 于玲, 等. 大跨度桥梁空间脉动风场的数值模拟[J]. 沈阳建筑大学学报: 自然科学版, 2010, 26(2): 238-243.
BAO Longsheng, LIU Ketong, YU Ling, et al. Numerical simulation of spatial fluctuating wind field on long-span bridges[J]. Journal of Shenyang Jian Zhu University: Natural Science, 2010, 26(2): 238-243.
[14] 李锦华, 李春祥. 超高层建筑脉动风速场模拟的改进谐波合成法[J]. 振动与冲击, 2008, 27(12): 151-156.
LI Jinhua, LI Chunxiang. Improved harmony superposition method(IHSM) for simulating the fluctuating wind velocity fields of super tall buildings[J]. Journal of Vibration and Shock, 2008, 27(12): 151-156.
[15] 罗俊杰, 韩大建. 大跨度结构随机脉动风场的快速模拟方法[J]. 工程力学, 2008, 25(3): 96-101.
LUO Junjie, HAN Dajian. A fast simulation method of stochastic wind field for long-span structures[J]. Engineering Mechanics, 2008, 25(3): 96-101.
[16] 《公路桥梁抗风设计指南》编写组. 公路桥梁抗风设计指南[M]. 北京: 人民交通出版社, 1996: 17-17.
Editing Group of Wind Resistance Design Guidebook for Highway Bridges. Wind resistance design guidebook for highway bridges[M]. Beijing: China Communications Press, 1996: 17-17.
[17] 刘海涛. 强风作用下列车、汽车同时通过公铁两用特大桥时的动力响应及行车安全性、舒适性研究[D]. 长沙: 中南大学土木建筑学院, 2011: 59-66.
LIU Haitao. Dynamic responses of train and automobile moving on highway-railway combined bridge under strong wind and analysis of running safety and riding comfort of vehicles[D]. Changsha: Central South University. School of Civil Engineering and Architecture, 2011: 59-66.
[18] 韩大建, 邹小江, 苏成. 大跨度桥梁考虑桥塔风效应的随机风场模拟[J]. 工程力学, 2003, 20(6): 18-22.
HAN Dajian, ZOU Xiaojiang, SU Cheng. Simulation of stochastic wind field of long-span bridges considering wind effects of the bridge towers[J]. Engineering Mechanics, 2003, 20(6): 18-22.
[19] 王之宏. 风荷载的模拟研究[J]. 建筑结构学报, 1994, 15(1): 44-52.
WANG Zhihong. Simulation of wind loading[J]. Journal of Building Structures, 1994, 15(1): 44-52.
(编辑 陈灿华)
收稿日期:2012-10-13;修回日期:2013-01-24
基金项目:国家自然科学基金资助项目(51078356);铁道部科技研究开发计划重大项目(2008G031-Q)
通信作者:郭文华(1969-),男,湖南常德人,教授,博士生导师,从事桥梁结构振动与稳定、风工程研究;电话:13973160678;E-mail:whguo@126.com