DOI: 10.11817/j.issn.1672-7207.2015.12.040
基于恒温边界一维非稳态传热模型测量固体材料热物性参数
陈清华1,董长帅1,马燕1,庞立1,刘泽功2
(1. 安徽理工大学 机械工程学院,安徽 淮南,232001;
2. 安徽理工大学 能源与安全学院,安徽 淮南,232001)
摘要:采用超级恒温水浴结合黄铜板形成恒温边界,通过控制试样尺寸(长和宽为厚度的8~10倍)结合侧壁面绝热层,保证在试样中产生准均匀一维热流。然后基于恒温边界下的一维非稳态传热模型,利用随机共轭梯度法对固体材料导热系数、比热容等进行参数估计反演计算。针对比热容灵敏度系数较低,参数反演估计误差较大的情况,估计热扩散率,并对比热容估计结果进行修正。建立实验测试装置,对松散煤体进行热物性测试,分析温度测量误差对估计结果的影响。最后,对玻璃等6种材料进行热物性测试分析。研究结果表明:利用随机共轭梯度法进行参数估计,准确性和抗不适定性较好,温度测量标准差达0.6时,仍能保证足够的参数反演精度(相对误差 <10%)。
关键词:固体材料;恒温边界;一维非稳态传热;反问题;随机共轭梯度法
中图分类号: TD752.1 文献标志码:A 文章编号:1672-7207(2015)12-4686-07
Test thermo-physical properties of solid material based on one dimensional unsteady heat transfer model in constant temperature boundary condition
CHEN Qinghua1, DONG Changshuai1, MA Yan1, PANG Li1, LIU Zegong2
(1. College of Mechanical Engineering, Anhui University of Science and Technology, Huainan 232001, China;
2. School of Energy and Safety Engineering, Anhui University of Science and Technology, Huainan 232001, China)
Abstract: By forming constant temperature boundary with super constant temperature bath and copper plate, in combination with the control measures of sample size (long and width are 8-10 times of thickness) and heat-insulating layer of sidewalls, the unsteady heat transfer model in first boundary condition was built. Then based on one dimensional unsteady heat transfer model in constant temperature boundary condition, using random conjugate gradient method, thermal conductivity and thermal capacity of solid material were estimated and calculated inversely. Considering that the sensitivity of thermal capacity is too low to inverse accurately, and that the estimation error of inversion calculation is very big, first, thermal diffusivity were estimated, and then thermal capacity was modified. Based on the built experimental system, the thermo-physical properties of the loose coal were tested. The influence of the temperature measurement error on the estimation results was discussed. Finally, six kinds of thermo-physical properties of material were tested and analyzed. The results show that the used algorithm has good accuracy and ill-posedness, even when the standard deviations of temperature reaches 0.6, thus inversion accuracy can be guaranteed (the relative error is less than 10%).
Key words: solid material; constant temperature boundary condition; one dimensional unsteady heat transfer; inverse problem; random conjugate gradient method
随着我国对节能及能源利用效率的日益重视,材料热物性及其测试方法方面的研究方兴未艾[1-2]。近年来,由于非稳态接触热源法具有快速、准确、可实现多参数测量的特点,在材料热物性测试中得到了更广泛的应用[3-6],但工程实际中仍存在一些问题。例如,目前多采用加热板、加热丝、加热棒等固态电热器作为加热热源,存在热源热流密度难以准确给定、加热探头热容及时间延迟性、热丝电阻温度依变性和功率波动等问题,且没有得到很好解决,这一定程度上影响了热物性参数测试精度。文献[7]采用一种陶瓷基底刻蚀双螺旋铂金属丝加热膜,热稳定性好且厚度极薄,可有效提高材料热物性测试精度,但成本较高且制作困难,难以推广应用。设有一长方体状试样上表面和两侧面均绝热,在某一时刻τ开始下表面保持恒温tw,将形成恒温边界条件下的一维非稳态传热问题,对此已具有明确的数学模型和解析解[8],但因具有2个以上的未知数(导热系数λ、比热容cp及βn),而无法直接基于解析解同时获取λ和cp等多个参数,目前尚没有在材料热物性测试中得到广泛应用。近年来已在多个领域得到应用的传热反问题为此提出了解决手段[9-12]。本文作者提出基于恒温边界条件下的一维非稳态传热模型,通过随机共轭梯度法[13]同时获取固体材料导热系数λ和比热容cp等多个参数。并对参数反演结果的影响因素进行了讨论分析。
1 传热数学模型
如图1所示的无限大平板试样,高度为△,上表面和侧面绝热,下表面突然与温度为tw的流体接触,试样中将产生恒温边界条件下的一维热传导过程[8],设试样导热系数为λ,密度为ρ、比热容为cp,且均为常数,其初始温度为t0,坐标原点取于试样上绝热面,则其非稳态导热微分方程及其初始、边界条件如下:
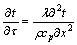 (1)
(1)
 (2)
(2)
式(1)的解析解如下:
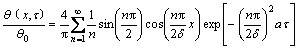 (3)
(3)
式中:θ(x,τ)为过余温度,θ=t-tw;热扩散率a=λ/(ρcp)。
恒温边界条件等价于毕渥数Bi→∞时的热对流边界条件,从而式(3)可改写为[8]

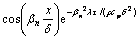 (4)
(4)
式中:βn为超越方程cot β=β/Bi的系列解,对应不同的Bi,β也不同(具体可查表),而在Bi→∞时,β1=1.570 8,βn=β1+(n-1)×π(n=1,2,…),试算表明,虽然式(4)包含无穷多项,但最多取15项即可满足固体材料热物性测试需求(相对误差<1%)。显然在试样密度ρ、导热系数λ、比热容cp及厚度△等物理参数已知的情况下,可计算得到试样内任意位置x任意时刻τ的温度分布情况,此即恒温边界条件下的非稳态传热数学模型。

图1 恒温边界下一维非稳态传热模型
Fig. 1 Unsteady heat transfer model in constant temperature boundary condition
2 热物性参数估计及可行性分析
2.1 参数估计
在试样热物性参数未知的情况下,根据测得的x=0处的温度数据对其反演推算,称参数估计。如前所述,从某一时刻开始试样下表面被温度为tw的热板加热,记为温度扰动u(τ),试样内任意一点处的温升记为Y(τ,η),其取决于试样的λ和cp等热物性,以及热板温度tw、时间、空间位置等参数,所有这些参数构成向量η:
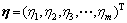 (5)
(5)
其中:m为参数数量,个。
密度ρ可实验测得,λ和cp为待估参数,首先获得x=0表面处k(k>2)个离散测点处的温度测量值Yi(τ,η)(i=1,…,k),然后基于参数估计值,通过式(4)计算各离散测点的计算值θi(τ,η) (i=1,…k),并与测量值进行对比:
 (6)
(6)
由于测量误差以及参数估计误差不可避免,从而必有ε(η)>0,最终参数估计过程可理解为基于式(4)进行迭代计算,最终使目标函数ε(η)→min。
2.2 可行性分析
参数向量η中的j个参数要能同时以足够的精度估计出来,必须满足在最小二乘估计意义下,测量时间范围内(参数估计的时间区间内),参数的灵敏度线性无关。灵敏度系数反映了参数βj的微小扰动对输出的影响。
利用二阶中心差商的有限差分格式灵敏度计算公式为
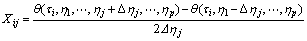 (7)
(7)
通常取△ηj=0.000 1ηj。
模型中待估计参数为:
η1=λ,η2=cp (8)
进行估计之前需要通过灵敏度分析判别此2个参数是否能同时估计。
为检验对不同导热系数的材料参数估计可行性,分别选取导热系数较大的玻璃和导热系数较小的松散煤体进行参数灵敏度分析。设玻璃物理参数为:厚度5 mm,密度2 530 kg/m3,导热系数0.701 W/(m·℃),比热容750 J/(kg·℃)。松散煤体物理参数为:密度1 010 kg/m3,试样厚度60 mm,粒度范围0~6 mm,导热系数0.14 W/(m·℃),比热容840 J/(kg·℃)。

图2 玻璃试样导热系数及比热容灵敏度
Fig. 2 Sensitivity coefficient of thermal conductivity and thermal capacity of glass sample
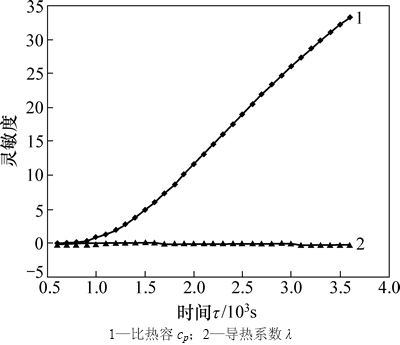
图3 松散煤体试样导热系数及比热容灵敏度
Fig. 3 Sensitivity coefficient of thermal conductivity and thermal capacity of loose coal sample
由图2和图3可以看出:玻璃和松散煤体的导热系数和比热容参数的灵敏度线性无关,但比热容cp灵敏度极小(仅10-3数量级),意味着直接对其进行估计误差将比较大[14]。
3 热物性参数估计系统设计
3.1 关键技术
在前述方法的基础上,要实现对材料热物性参数的准确估计,需要解决一维非稳态传热条件、恒温边界构建、参数估计算法、测试系统构建等关键问题。
3.1.1 一维非稳态传热条件的实现
当试样被面热源加热时,侧壁面边界上必然会产生热损,从而不再是一维非稳态传热。研究发现,通过在侧面设绝热层,同时控制试样长、宽与厚度的比值(长和宽为厚度的8~10倍)[15],即可在试样中产生准一维非稳态传热过程。本文中的所有试样尺寸均按照此标准制作,以保证一维非稳态传热条件。
3.1.2 参数估计流程
虽然基于本文提出的模型可实现材料导热系数λ、比热容cp的同时估计,但cp灵敏度过低而无法准确估计。由于式(4)中只有λ/(ρcp)项即热扩散率a这一个未知数,可首先将a估计出来,然后利用其对估计的cp进行修正。
此处采用随机共轭梯度法进行求解[13],参数估计流程如下:
1) 反演估计a;
2) 将待估参数向量更改为η=(λ,cp)T,估计材料λ及cp(原始估计值);
3) 根据a及λ估计值修正cp的原始估计值,最终得到修正后的cp*。
理论上每个特定时刻τ均可得到一组数值λ和cp*,对计算出的一系列值求加权平均作为最终参数估计值,同时可消除测试过程中因干扰因素造成的个别数据波动影响。
3.2 系统结构总体设计
系统总体结构原理如图4所示。
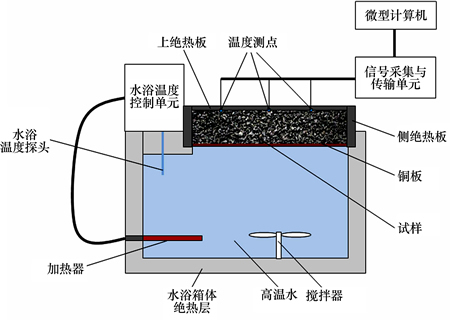
图4 测试装置简图
Fig. 4 Diagram of testing system
3.2.1 恒温边界的实现
直接利用超级恒温水浴构建恒温边界,由加热元件、温控装置、水箱等组成,其内置循环水泵和搅拌器,与固体热源相比温度均匀性和稳定性更好。温控范围为5~95 ℃,恒温精度可达0.05 ℃。设温度为tw的高温水通过3 mm厚黄铜板与试样传递热量,试样与铜板接触良好,传热模型如图5所示。
高温水与铜板接触的初始阶段,黄铜板内的温度首先要经历一个温度均衡过程,即温度分布曲线从PA→PB→PC→PD→PE的变化过程,并最终趋向于与高温水保持一致,与此同时试样内温度变化呈BF→CG→DH→EI的变化过程,但真正满足恒温边界条件是黄铜板内的温度分布曲线为PE开始,之前均处于非稳态阶段(非恒温状态)。但实验测试表明,3 mm厚黄铜板与利用搅拌器搅动的90 ℃热水接触,在小于2 s时间内即可达到温度均衡,从而可忽略铜板内的温度均衡时间因素带来的恒温边界设定误差。

图5 水、黄铜板、试样对流传热模型
Fig. 5 Heat convection model of water, brass plate and sample
3.2.2 松散材料与固体材料测试通用性问题
固体板状成型材料可利用水介质加热,而松散材料则无法直接与水介质接触,针对此特点设计了试样盒。上盖和侧壁均为绝热材料,防止侧向传热和环境温度影响试样内的温度场。底板为黄铜材质,以保证与高温水接触时的温度均匀性。设试样与黄铜板接触良好,即可建立恒温边界下的松散材料一维非稳态传热模型。
3.2.3 温度测试准确性及可靠性
通常固体成型材料接近各向同性,温度测试值与位置关系不大,但松散材料因多孔介质结构特征造成温度测试值与测点位置具有一定的随机关联性。针对此,采用T型高精度热电偶作为温度传感器,温度信号通过PLC+热电偶模块采集与传输,抗干扰性好,测温精度等级可达0.1级。为了避免松散材料多孔结构随机因素的影响,布置多个温度测点,取多个温度测量值的加权平均作为最终结果。
4 热物性测试实验分析
4.1 松散物料热物性参数测试实验
此处利用潘一矿原煤进行热物性参数估计实验,首先利用筛网将煤样筛分粒度为0~5 mm的试样,然后放入内腔长×宽×高为600 mm×600 mm×60 mm的试样盒,填充密度为930 kg/m3,环境温度为20 ℃,将恒温水浴设定为90 ℃。在煤样中同一水平布置3个温度测点,取平均值作为最终测试值,从左至右分布编为1号、2号和3号,且均离侧壁面一定距离,防止侧向热损造成影响。某一时刻τ突然将试样盒底部黄铜板与高温水接触,同时测定煤样上部绝热面处的温度变化,估计煤样热物性参数。实验共进行了3 h,温度采样间隔为600 s,考虑到采样开始阶段温度稳定性不佳,以及因时间累计效应后期采样数据可能会受外界因素影响更大等因素,实际只取1 800 s和7 200 s范围内的温升数据进行计算。图6所示为各测点温度变化曲线。
热扩散率a初始猜测值为1.0×10-7 m2/s,导热系数λ和cp初始猜测值分别为0.1 W/(m·℃)和800 J/(kg·℃),取参数估计结果如表1所示。
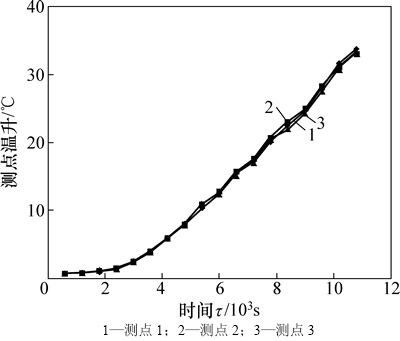
图6 1~3号测点温升曲线
Fig. 6 Temperature rise curves of measuring points No. 1-3
表1 参数估计值
Table 1 Estimation results of parameters
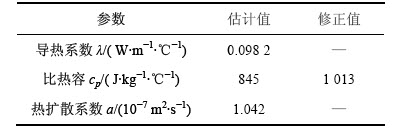
从表1可以看出:热扩散率和导热系数估计结果与采用热线法测得的结果较为接近[16],但比热容因灵敏度系数较低造成相对误差较大(大于20%),从而取修正后的结果cp*作为最终估计值。为进一步验证测算结果准确性,对同一种试样在相同条件下进行了3次实验,通过测算值彼此接近的程度衡量实验测试结果可重复精度,相对误差为
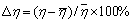 (9)
(9)
式中:η为单次实验值; 为次测算值的平均值。具体结果如表2所示。
为次测算值的平均值。具体结果如表2所示。
由表2可以看出:导热系数与热扩散率参数反演结果与平均值最大相对误差分别为2.22%和0.85%,精度符合要求。对同类型试样采用Shotherm QTM-D2型导热系数速测仪测导热系数,并用差热分析仪测比热容,测试结果分别为0.098 W/(m·℃)和1 015 J/(kg·℃),换算得热扩散率为1.038×10-7 m2/s,与本文方法所测结果基本一致。
表2 参数估计实验可重复精度分析
Table 2 Repeatability accuracy of parameters estimation

4.2 参数估计结果准确性分析
4.2.1 理论计算与数值仿真结果对比
为验算参数估计结果的准确性,将获取的导热系数λ和比热容cp*代入式(4),计算τ为0~10 800 s的温度理论值,并与试验结果对比。此外在Fluent中建立仿真模型,模拟了恒温边界条件下煤样中的温度场变化情况。图7所示为2号测点位置处的温度变化理论计算和仿真结果。
由图7可以看出:理论计算值与Fluent数值仿真值基本吻合,说明参数估计结果是准确的。值得注意的是,从约7 800 s开始,试验数据与理论值误差开始增大,并呈逐渐上升趋势。原因可能是,煤样上表面被绝热材料覆盖,热量传递此处后无法及时扩散,造成热量积聚,初始阶段积聚的热量不多,对测点温升影响不明显,而随着时间延长,影响逐渐增大,造成测点温升高于真实值,称为热穿透效应。从而应适当控制试验时间,以避免热穿透效应对测点温升影响,造成参数估计误差过大。
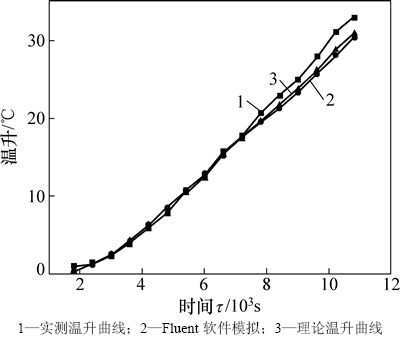
图7 实测、理论与数值仿真温升曲线对比
Fig. 7 Contrast between measurement, theoretical and simulating temperature rise
4.2.2 参数估计影响因素分析
参数估计结果通常受初始猜测值、温度测量误差等影响,由于随机共轭梯度法可以有效消除初始猜测值的影响[13],从而此处只对温度测量误差的影响进行讨论分析。相对误差ηr为
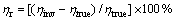 (10)
(10)
式中:ηinv和ηtrue分别为参数反演值和真实值。
由于测温系统中热电偶及数据采集与传输装置的精度和稳定性因素导致温度测量值具有一定随机特性,表现为测量误差,即温度测量值Y(τj,η)与真实值间存在差值,可用下式表示:
Y(τj,η)test=Y(τj,η)true+ω△ (11)
式中:ω为一标准正态分布的随机数(-2<ω<2);△为标准差,分别给定为0.2,0.4和0.6。设a,λ和cp的初始猜测值分别为1×10-7m2/s,0.1 W/(m·℃)和900 J/(kg·℃),各参数反演结果分别如表3和表4所示。
表3 温度测量误差对热扩散系数估计结果的影响
Table 3 Influence of temperature measurement error on inversed results of thermal diffusivity
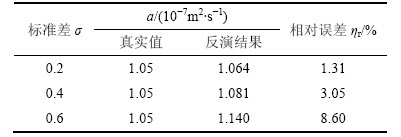
表4 温度测量误差对导热系数估计结果的影响
Table 4 Influence of temperature measurement error on inversed results of thermal conductivity
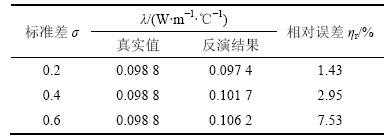
从表3和4可以看出:温度测量误差对参数估计结果有影响。当σ为0.6时,热扩散系数估计误差可达8.60%,导热系数估计相对误差最大可达7.53%,但均小于10%。事实上,而本系统采用热电偶作为测温传感器,利用PLC测温模块采集数据,能够满足精度要求,同时具有较好的抗干扰能力。实验证明,温度小于100 ℃时的测量标准差σ远远小于0.6。
4.3 板状固体材料热物性测试实验
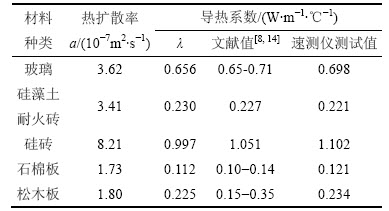
对玻璃、松木板、石棉板、硅砖、硅藻土耐火砖等分别进行了热物性测试,并将数据与相关文献结果进行了对比,结果如表5所示。
从表5可以看出:利用本系统测硅藻土耐火砖、石棉板、松木板热物性参数,与相关文献数据基本一致,且导热系数测试结果与速测仪测试结果基本相同,相对误差<5%。但玻璃导热系数与速测仪测试结果相对误差接近7%,经分析这与玻璃试样厚度较小,受黄铜板温度均衡滞后时间影响较大有关,而硅砖导热系数测试结果与相关文献结果的相对误差也有5.4%。本装置较为适用于低导热系数固体材料热物性测试。
表5 板状固体材料热物性测试结果
Table 5 Measurement results of plate solid material’s thermo-physical properties
5 结论
1) 提出了基于恒温边界一维非稳态传热模型,利用随机共轭梯度法,估计固体材料导热系数及热扩散率。与采用固体面热源加恒温控制器的方式相比,利用超级恒温水浴结合铜板构建恒温边界,更易于实现,温度均匀性和稳定性好。
2) 可以同时估计导热系数λ与比热容cp,但cp灵敏度较小,对其进行直接估计误差将较大。先估计热扩散系数a和导热系数λ,再对cp进行修正,能够获得满意的参数估计精度,虽受温度测量误差影响明显,但当标准差σ达到0.6时,参数反演结果相对误差仍不超过10%。
3) 导热系数较低的石棉板、硅藻土耐火砖、松木板测试结果与相关参考数据较吻合,相对误差<5%,而可能受铜板温度均衡滞后效应影响,玻璃和硅砖等导热系数较大的材料,相对误差超过了5%,因此,本文方法更适用于导热系数较低的绝热材料热物性测试。
参考文献:
[1] 陈桂生, 廖艳, 曾亚光, 等. 材料热物性测试的研究现状及发展需求[J]. 中国测试, 2010, 36(5): 4-8.
CHEN Guisheng, LIAO Yan, ZENG Yaguang, et al. Development requirements and research status of thermal physical properties testing[J]. China Measurement & Test, 2010, 36(5): 4-8.
[2] 于帆, 张欣欣, 何小瓦. 材料热物理性能非稳态测量方法综述[J]. 宇航计测技术, 2006, 26(4): 23-29.
YU Fan, ZHANG Xinxin, HE Xiaowa. A review of measurement of thermo-physical properties of materials by transient method[J]. Journal of Astronautic Metrology and Measurement, 2006, 26(4): 23-29.
[3] Hadi S, Nishitani M, Wijayanta A T, et al. Contact measurement of thermal conductivity and thermal diffusivity of solid materials: Experimental validation of feasibility with a prototype sensor[J]. International Journal of Heat and Mass Transfer, 2014, 69(1): 256-263.
[4] Xu G, LaManna J M, Clement J T, et al. Direct measurement of through-plane thermal conductivity of partially saturated fuel cell diffusion media[J]. Journal of Power Sources, 2014, 256(6): 212-219.
[5] Zhang P, Ma Z W, Shi X J, et al. Thermal conductivity measurements of a phase change material slurry under the influence of phase change[J]. International Journal of Thermal Sciences, 2014, 78(4): 56-64.
[6] 陈清华, 张国枢, 秦汝祥, 等. 热线法同时测松散煤体导热系数及热扩散率[J]. 中国矿业大学学报, 2009, 38(3): 336-340.
CHEN Qinghua, ZHANG Guoshu, QIN Ruxiang, et al. Measurements of thermal conductivity and diffusivity of loose coal using a hot-wired method[J]. Journal of China University of Mining & Technology, 2009, 38(3): 336-340.
[7] 王强, 戴景民, Coppa P. 基于保护平面热源法的防隔热材料热物性测量[J]. 天津大学学报, 2010, 43(12): 1086-1092.
WANG Qiang, DAI Jingmin, Coppa P. Thermophysical property measurement of thermal protective material by guarded plane source method[J]. Journal of Tianjin University, 2010, 43(12): 1086-1092.
[8] 苏亚欣. 传热学[M]. 天津: 华中科技大学出版社建筑分社, 2009: 32-50.
SU Yaxin. Heat transfer theory[M]. Tianjin: Construction Bureau of Huazhong University of Science & Technology Press, 2009: 32-50.
[9] 卢涛, 刘波, 卢红光. Levenberg-Marquardt算法求解三维圆管稳态导热反问题[J]. 热科学与技术, 2010, 9(2): 133-138.
LU Tao, LIU Bo, LU Hongguang. Solution of inverse steady-state heat conduction problem using Levenberg- Marquardt method for three-dimensional pipeline[J]. Journal of Thermal Science and Technology, 2010, 9(2): 133-138.
[10] 刘慧开, 杨立, 孙丰瑞. 基于传热反问题的异步电机参数估计方法研究[J]. 中国电机工程学报, 2006, 26(22): 151-156.
LIU Huikai, YANG Li, SUN Fengrui. Estimation method for parameters of asynchronous motor based on inverse heat conduction problem analysis[J]. Proceedings of the CSEE, 2006, 26(22): 151-156.
[11] 刘福国, 郝卫东, 胡志宏, 等. 采用炉膛燃烧和传热反问题在线测量超临界直流锅炉燃煤发热量[J]. 中国电机工程学报, 2013, 33(5): 1-8.
LIU Fuguo, HAO Weidong, HU Zhihong, et al. On-line determination of the calorific value of fired coals in supercritical pressure once-through boiler based on inverse furnace combustion and radiation problems[J]. Proceedings of the CSEE, 2013, 33(5): 1-8.
[12] 石宏臣, 张晓怀, 孙丰瑞, 等. 基于红外成像测温的储罐液位传热反问题识别方法[J]. 化工学报, 2012, 63(12): 3771-3775.
SHI Hongchen, ZHANG Xiaohuai, SUN Fengrui, et al. Inverse heat transfer algorithm for liquid-level detection of storage tank based on infrared imaging temperature measurement[J]. CIESC Journal, 2012, 63(12): 3771-3775.
[13] 朱培民, 王家映. 共轭梯度法[J]. 工程地球物理学报. 2008, 5(4): 381-386.
ZHU Peimin, WANG Jiaying. Conjugate gradient method[J]. Chinese Journal of Engineering Geophysics, 2008, 5(4): 381-386.
[14] 乐凯, 张欣欣, 于帆. 基于三点法的柱状生物组织热特性参数估计[J]. 工程热物理学报, 2005, 26(5): 838-840.
LE Kai, ZHANG Xinxin, YU Fan. Estimation of thermal parameters of cylindrical living tissues using three-point method[J]. Journal of Engineering Thermophysical, 2005, 26(5): 838-840.
[15] 周孑民, 朱再兴, 谢东江, 等. 常功率平面热源法测试耐火材料热物性的研究[J]. 中南大学学报(自然科学版), 2011, 42(5): 1467-1472.
ZHOU Jiemin, ZHU Zaixing, XIE Dongjiang, et al. Thermal physical property of refractory material measured by plane heat source method with constant heat rate[J]. Journal of Central South University (Science and Technology), 2011, 42(5): 1467-1472.
[16] 陈清华. 松散煤体热物性测试及其温度场分布规律研究[D]. 淮南: 安徽理工大学能源与安全学院, 2009: 66-67.
CHEN Qinghua. Study on thermo-physical properties measurement and temperature field distribution of loose coal bulk[D]. Huainan: Anhui University of Science and Technology. School of Mining and Safety Engineering, 2009: 66-67.
(编辑 赵俊)
收稿日期:2014-12-12;修回日期:2015-03-16
基金项目(Foundation item):国家自然科学基金资助项目(50974003);安徽省自然科学基金资助项目(1408085ME107);中国博士后科学基金资助项目(2014M561807);安徽省高校优秀青年基金重点资助项目(2011SQRL041ZD)(Project (50974003) supported by the National Natural Science Foundation of China; Project (1408085ME107) supported by the Natural Science Foundation of Anhui Province; Project (2014M561807) supported by the National Science Foundation for Post-doctoral Scientists of China; Project (2011SQRL041ZD) supported by the Education Department of Anhui Province)
通信作者:陈清华,博士(后),副教授,从事煤矿安全、传热学、矿山机械领域研究;E-mail:ahhnds@163.com