Article ID: 1003-6326(2005)03-0553-07
Strength of deformation-processed Cu-Fe in-situ composites
GE Ji-ping(葛继平), ZHAO Hong(赵 红), YAO Zai-qi(姚再起)
(Department of Materials Science and Engineering, Dalian Jiaotong University,
Dalian 116028, China)
Abstract: The strength of the deformation-processed Cu-Fe in-situ composite was conducted by material test system(MTS). The results show that the strength increases with the increasing deformation strain and iron content, which is greater than that of the calculated value based on the rule of mixture. The mechanism of strengthening was analysed and evidenced by interface barrier. The correlation between the strength and the thickness of copper phase(tCu) obeys Hall-Petch relationship and can be described well by geometrical necessary dislocation model and interface as dislocation source model.
Key words: deformation-processed; Cu-Fe in-situ composite; strength CLC
number: TB323 Document code: A
1 INTRODUCTION
The term in-situ composites is used in this paper to describe materials where an align fibrous microstructure is created by very heavy wire-drawing. The strengths obtained in such composites can be much greater than that expected from the calculated value based on the rule of mixture[1, 2]. Several models have been proposed to explain the phenomena and to set up the strengthening mechanisms. The first model is dislocation substructure strengthening model. The analysis indicates that the dislocations are blocked at the interface between the fiber and the matrix during wire-drawing owing to the incompatibility of plastic deformation of the two phases, and consequently formed high density dislocations, which generated strengthening effects[1-5]. The second is interface barrier model, which attributes the strength to the difficulty of propagating plastic flow through the fiber/matrix interface[6, 7]. The third is the extended rule of mixture, which accounts for the dislocation arrangements at the phase boundaries, the textures and the morphology of both phases[8, 9]. Some of these models simulate the strength well, however less research work has been done on the strengthening mechanism of deformation processed Cu-Fe in-situ composite. In this paper, the mechanical properties of deformation processed Cu-Fe in-situ composite and its relating factors were investigated and analyzed, the strengthening mechanism and relationship between the mechanical properties and micro-structure were explored, finally the strengthening model was built up.
2 EXPERIMENTAL
Cu-11.5%Fe and Cu-17.5%Fe billets with the sizes of 22mm in diameter and 70mm in length after surface machining were prepared by inductive melting. From the cast cylindrical ingots the wires were produced by rotary swaging, rolling and drawing. During swaging the sample diameter was reduced from 22mm to 16mm, and by rolling from 16mm to 8.5mm. Finally wire-drawing was conducted until the diameter became 6mm. Next, the samples were subjected to two deformation routes. 1) Samples were drawn at room temperature(RT) without intermediate heat treatment(HT). 2) Wire-drawing with intermediate heat treatment. It is: 6mm→HT1→3mm→HT2→1.5mm→HT3→1, 0.8, 0.5, 0.3, 0.2mm. The intermediate heat treatment routes are→HT1: holding at 500℃ for 1h, cooling from 500℃ to 400℃ for 48h; HT2: holding at 450℃ for 1h, cooling from 450℃ to 350℃ for 48h; HT3: holding at 400℃ for 1h, cooling from 400℃ to 300℃ for 48h. The intermediate heat treatments were carried out in vacuum furnace. The deformation strain was defined as the natural logarithmic form: η=ln(A0/Af), where A0 is the initial cross-sectional area and Af is the final cross-sectional area.
All tensile tests were conducted at RT with strain rate of (1.0-3.0)×10-5s-1. The fracture morphology of the tensile specimens were observed on a JSM-6360LV SEM.
3 RESULTS
3.1 Microstructure
Fig.1(a) shows the microstructures of the as-cast Cu-17.5%Fe alloy. The primary Fe dendrites(dark) are embedded in the Cu matrix(light).Fig.1(b) shows a longitudinal section of the as-drawn wire, and it can be seen that a significant elongation of the Fe dendrites has occurred during the wire-drawing.

Fig.1 Optical micrographs of Cu-17.5% Fe
3.2 Strength
Fig.2 shows the correlation between the strength of deformation-processed Cu-11.5%Fe in-situ composite(A) and the deformation strain(η). The letter “A” means without intermediate heat treatment during wire drawing. It is clear that both the ultimate tensile strength(UTS) and the yield strength(YS) increase with the increasing deformation strain, and the yield strength is in linear relationship with deformation strain.
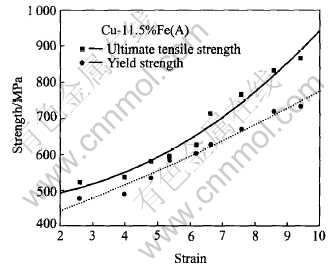
Fig.2 Strength of deformation-processed Cu-11.5%Fe in-situ composite(A) with progressing wire deformation
Fig.3 shows the influence of the Fe content and deformation strain on the UTS and YS. Both the UTS(Fig.3(a)) and YS(Fig.3(b)) of the deformation-processed Cu-11.5%Fe in-situ composite(B) and the deformation-processed Cu-17.5% Fe in-situ composite(B) increase with the increasing deformation strain. It is obvious that the iron content plays an important part on the strength of deformation-processed Cu-Fe in-situ composite. The higher the iron content in deformation-processed Cu-Fe in-situ composite is, the greater the strength increases.
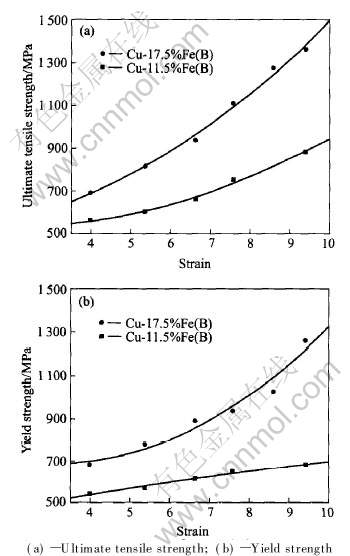
Fig.3 Effect of Fe content on strength of deformation-processed Cu-Fe in-situ composites(B)
The study on the strain hardening of pure Cu points out that the strength of pure Cu wire reaches a saturated value around 450-460MPa with the increasing deformation strain. The behavior is the result of dynamic recovery, which results in equilibrium between the multiplication and annihilation of dislocations[10, 11]. The strength of pure Fe wire keeps a linear relationship with strain[12], and is greater than that of pure Cu at the same deformation strain[13]. Obviously the contribution to strength by pure Fe is more than that by pure Cu. Therefore, the higher the Fe content in deformation-processed Cu-Fe in-situ composites is, the greater the strength is. The same phenomena are observed in the study of deformation-processed Cu-Nb in-situ composite. As the Nb content increases, the strength increases[14].
From Figs.2 and 3, it can be concluded that the effect of intermediate heat treatments on the strength of the deformation-processed Cu-11.5%Fe in-situ composite is insignificant. Some researches pointed out that the deformed fibers could be broken up or spheroidized during intermediate heat treatment, and much thinner fibers formed after progressing wire deformation. That means, the intermediate heat treatment could make the fibers finer[15]. In this study, the intermediate heat treatment temperature is not very high, consequently no obvious breakup of Fe fibers is found under SEM observation. But, the SEM observation indicates that the intermediate heat treatment can accelerate the change from Fe dendrites to fibers[16]. It is certain that the heat treatment softens the Fe phase and readily enables the formation of fibers in the later deformation process; therefore the appearance of small fibers enhances the strength and compensates the loss of strength during heat treatments. It is also seen that Fe particles precipitate out from Cu matrix during heat treatments and change into fibers in the later deformation process, which evidences the fiber strengthening effects.
Fig.4 shows the correlation of the strength and the thickness of Cu phase (tCu). When tCu is small, the strength increases sharply as the tCu decreases; at the same thickness, the strength increases with the Fe content. Fig.4 displays the linear correlation between strength of deformation-processed Cu-Fe in-situ composite and t-1/2Cu. It is clear that the slope of the lines having higher Fe content is greater than that of having lower Fe content, that is, the strength dependence of t-1/2Cu of higher Fe content composite varies more intensively. Meanwhile, the different deformation routes result in different changing tendency and route A enhances the strength more greatly than that of route B.
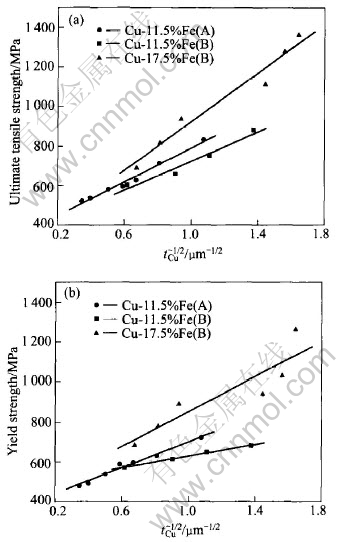
Fig.4 Relationship between strength and thickness of Cu phase(tCu) in deformation-processed Cu-Fe in-situ composites
It is generally accepted that the strength of a composite obeys the rule of mixture (ROM). Thus the strength of deformation-processed Cu-Fe in-situ composite could be expressed as
σc=σCuφCu+σFeφFe(1)
where σCu and σFe are the strength of Cu and Fe phase, respectively; φCu and φFe are the corresponding volume fractions.
Based on the conclusions of Funkenbusch[13] and solid solution strengthening increment 70MPa due to Fe solution in Cu phases, the strength values for Cu and Fe can expressed by
σCu(Fe)=228+70+156η0.24
σFe=330+153η
The comparisons of the experimental data with the theoretical calculated values by the ROM are shown in Fig.5. The results got from deformation- processed Cu-11.5%Fe in-situ composite(A) are well matched with the calculated values when η≤6; however the values of ROM are smaller than those of experiments when η≥6. The identical results can be referred to Ref.[10]. At the initial stage of deformation, the mechanism can be well interpreted by the traditional rule of mix- ture, but when the deformation strain gets greater, reaching nano-level in size, the real strength is much greater than that of rule of mixture.
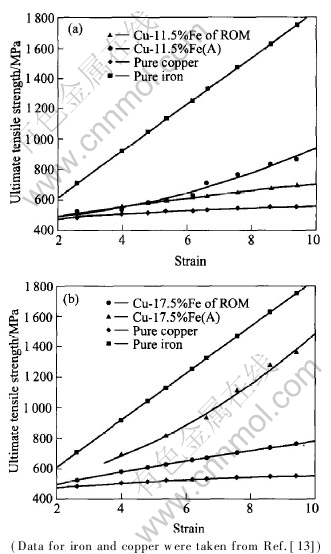
Fig.5 Ultimate tensile strengths of deformation-processed Cu-Fe in-situ composites compared with those calculated based on rule of mixture strength
3.3 Fracture morphologies
Morphologies of fracture surfaces of deformation-processed Cu-11.5%Fe in-situ composites(A) are shown in Fig.6. They exhibited ductile fractures. The fracture surfaces show many dimples, and the dimples are relatively fine with higher deformation strain. The diameters of the fracture cross sections are measured and the shrinkage rate are ψ=32.2% for η=3.98 and ψ=27.8% for η=6.63.
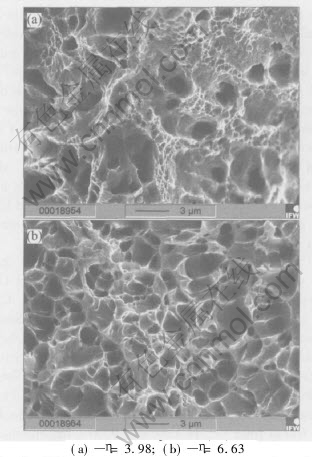
Fig.6 SEM micrographs of fracture surface for deformation-processed Cu-11.5%Fe in-situ composites(A)
4 DISCUSSION
Figs.4 and 5 indicate that the correlation between the strength of deformation-processed Cu-Fe in-situ composite and Cu phase thickness is conformed to the Hall-Petch relationship and the strength is higher than theoretically calculated value based on ROM, which are all in consistence with others conclusions[1, 2, 17]. The research work on the hardness of nano-sized Cu-Fe alloy, which was fabricated by high-energy grinder and annealing treatments, demonstrates that real hardness is higher than the calculated one based on ROM and a maximum value appears when the Fe content is 70%(volume fraction). This is the result of interface hardening effects. The changing of slip system during the stress passing through Cu/Fe interface generates high-density geometrical necessary dislocations at the interface. The interface effects of Cu/Fe system are stronger than those of Cu/Cu and Fe/Fe accordingly[18]. There are many analyses on the mechanism of strengthening, basically being classified into two aspects: 1) strengthening is attributed to the dislocation; 2) strengthening is a direct consequence of the presence of barriers (filaments) in the materials. Factually, they are all related to the interfaces between the fiber and the matrix, which affects the density of dislocations, their structure and movement. The reason why the strength of deformation-processed Cu-base in-situ composite is greater in experiments than in calculating by ROM is that the system has high interfaces density[19] and the blockage of the movement of dislocations[20]. There were also views that the interface absorbed dislocations and created greater stress due to mismatch at the interface, which brought about higher strength in experiments[21]. Anyway, the interface of Cu/Fe is an indispensable factor when the strength of the deformation-processed Cu-Fe in-situ composites is in consideration. The geometrical necessary dislocation model and interface as dislocation source model are discussed in the following.
4.1 Geometrical necessary dislocation model
The geometrical necessary dislocation was firstly found in the plastic deformation of non-homogeneous material[22]. Composite materials comprising phases with pronounced difference in their respective deformation behavior develop a strong deformation gradient. The gradient is then compensated for by generation of dislocation, referred to as geometrical necessary dislocation. The stronger the gradient is, the higher the density of geometrical necessary dislocations is[3, 4]. Ashby[23] gave out a formula on the density of geometrical necessary dislocations with small deformation strain.

where ρG is the density of geometrical necessary dislocations; K is geometrical constant; η is strain; λ is space between phases.
K is the compatibility coefficient, which reflects the incompatibility of the shear strain of two phases and depends on the mismatched degree between two phases. It was proved that ≈Kb[4] (: the rotation angle, b: burgers vector), therefore the maximum value of K could be figured out by putting the maximum rotation angle 90° during a wire-drawing process into the formula, which equals 6.3×109/m.
According the previous researches, the spacing between two phases could be replaced by, consequently a more proper expression of the density is drawn out:
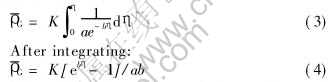
After integrating:

When the deformation strain is small enough(η1), Eqn.(2) is more accurate; when η1, the following is better,

The strength of deformation-processed Cu-Fe in-situ composite is the sum contribution of geometrical necessary dislocation ρG effects and statistical dislocations ρS based on the bulk strength:
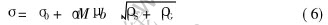
where σ0 is lattice friction force, M is Talyor coefficient, μ is shear modulus, ρS is statistical density of dislocation. All parameters are referred to the reference[24].
The calculated densities of geometrical necessary dislocations based on Eqn.(5) and the correlation between the thickness of Fe fiber and the strain of the composite are as follows: when K=7×108/m[3] and η=2.6-9.4, the ρG value of deformation processed Cu-11.5%Fe in-situ composite(A) and deformation processed Cu-17.5%Fe in-situ composite(B) lie in the range of 1.8×1010-2.9×1011cm-2 and 4.4×1010-6.7×1011cm-2, respectively. When K=2×109/m[4], that of deformation processed Cu-17.5%Fe in-situ composite(B) is 1.3×1011-1.9×1012cm-2. The higher the Fe content is, the higher the dislocation density is. The reason is that with the same deformation strain, higher Fe content leads to higher interface density between Cu and Fe phases.
Fig.7 shows the comparison between experimental and calculated values. It can be seen that the data match well when the compatibility coeffi-cient K=7×108/m for deformation processed
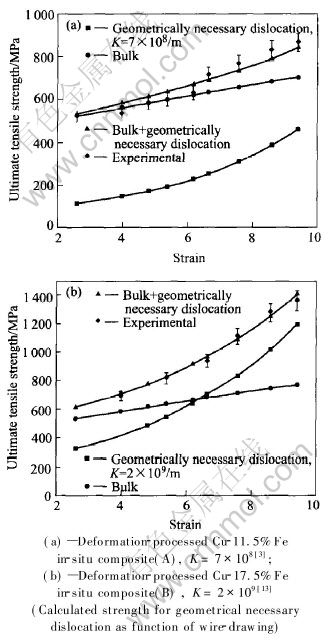
Fig.7 Comparison between calculated results and experimental ones
Cu-11.5%Fe in-situ composite(A) and K=2×109/m for deformation processed Cu-17.5%Fe in-situ composite(B).
4.2 Interface as dislocation source
Spitzig et al[6, 7] put forward that the interfaces of Cu/Nb acted as sources of dislocations which controlled plastic flow across the interfaces. In the model the number of dislocations generated per unit of deformation is proportional to the interfacial surface area per unit volume(S). Hong[21] modified the Hall- Petch equation by taking total area of phase boundaries into consideration:

where S is the total area of the phase boundaries, k′ is a constant.
The comparison between experimental strength and calculated strength based on this model is demonstrated in Fig.8. The results when
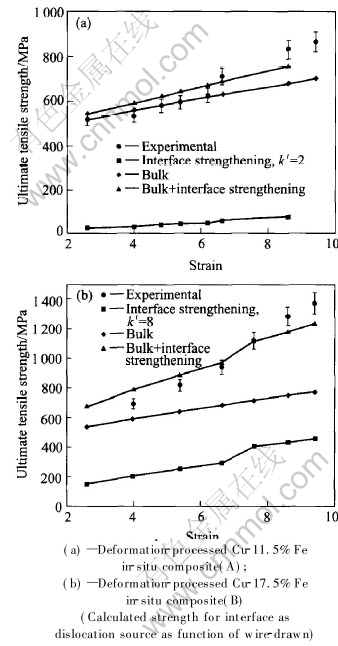
Fig.8 Comparison between calculated results and experimental ones
k′=2MPa·mm-1/2 are similar to each other for the deformation processed Cu-11.5%Fe in-situ composite(A), while k′=8MPa·mm-1/2, the data fit well with the deformation processed Cu-17.5%Fe in-situcomposite(B).
From the above results the conclusion can be educed that the geometrical necessary dislocation model and interface as dislocation source model can describe the strength of deformation- processed Cu-Fe in-situ composite.
5 CONCLUSIONS
1) The strength of deformation processed Cu-Fe in-situ composite increases with the increasing deformation strain and Fe content, and its dependence on the thickness of Cu phase obeys Hall-Petch relationship.
2) The strength can be described by geometrical necessary dislocation model and interface as dislocation source model with a fitting parameters.
Acknowledgements
The work was finished in Leibniz-Institute of Solid State and Materials Research Dresden, Germany. The authors thank Professor Ludwig Schultz and Professor Jürgen Eckert for their generous supports.
REFERENCES
[1]Go Y S, Spitzig W A. Strengthening in deformation-processed Cu-20%Fe composites [J]. J Mater Sci, 1991, 26: 163-171.
[2]Spitzing W A, Downing H L, Laabs F C, et al. Strength and electrical conductivity of a deformation-processed Cu-5 pct Nb composite [J]. Metall Trans, 1993, A24: 7-14.
[3]Funkenbusch P D, Courtney T H. On the strength of heavily cold worked in-situ composites [J]. Acta Metall, 1985, 33: 913-922.
[4]Funkenbuch P D, Lee J K, Courtney T H. Ductile two-phase alloys: prediction of strengthening at high strains [J]. Metall Trans, 1987, A18: 1249-1256.
[5]Funkenbusch P D, Courtney T H. On the role of interphase barrier and substructural strengthening in deformation processed composite materials [J]. Scripta Met, 1989, 23: 1719-1724.
[6]Spitzig W A. Strengthening in heavily deformation processed Cu-20%Nb [J]. Acta Metall Mater, 1991, 39: 1085-1090.
[7]Spitig W A, Pelton A R, Laabs F C. Characterization of the strength and microstructure of heavily cold worked Cu-Nb composites [J]. Acta Metall, 1987, 35: 2427-2442.
[8]Hangen U, Raabe D. Modelling of the yield strength of a heavily wire drawn Cu-20%Nb composite by use of a modified linear rule of mixtures [J]. Acta Metall Mater, 1995, 43: 4075-4082.
[9]Raabe D, Hangen U. Simulation of the yield strength of wire drawn Cu-based in-situ composites [J]. Computational Materials Science, 1996. 5: 195-202.
[10]Spitzig W A, Biner S B. Comparison of strengthening in wire-drawn or rolled Cu-20%Nb with a dislocation accumulation mode [J]. J Mater Sci, 1993, 28(17): 4623-1629.
[11]Thilly L, Véron M, Ludwig O, et al. High-strength materials: in-situ investigations of dislocation behaviour in Cu-Nb multifilamentary nanostructured composites [J]. Philos Mag, 2002, A82: 925-942.
[12]Langford G, Cohen M. Strain hardening of iron by severe plastic deformation [J]. Transactions of the ASM, 1969, 62: 623-638.
[13]Funkenbusch P D, Courtney T H. Microstructural strengthening in cold worked in-situ Cu-14.8%Fe composites [J]. Scripta Metall, 1981, 15: 1349-1354.
[14]Kasaba K, Katagiri K, Shoji Y, et al. Stress/strain dependence of critical current in Nb3Sn superconducting wires stabilized with Cu-Nb microcomposites-effect of Nb content [J]. Cryogenics, 2001, 41(1): 9-14.
[15]Hong S I, Hill M A. Microstructural stability and mechanical response of Cu-Ag microcomposite wires [J]. Acta Metall Mater, 1998, 46: 4111-4122.
[16]GE Ji-ping, YAO Zai-qi. High strength and high electrical conductivity deformation-processed Cu-Fe in-situ composites [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(4): 568 -573.(in Chinese)
[17]Song J S, Hong S I. Strength and electrical conductivity of Cu-9Fe-1.2Co filamentary microcomposite wires [J]. Journal of Alloys and Compounds, 2000, 311(2): 265-269.
[18]He L, Ma E. Processing and microhardness of bulk Cu-Fe nanocomposites [J]. Nanostructured Materials, 1996, 7(3-4): 327-339.
[19]Konstantinidis D A, Aifantis E C. On the “anomalous” hardness of nanocrystalline materials [J]. Nanostruct Mater, 1998, 10: 1111-1118.
[20]Yao Y, Wang T C. The modified peierls-nabarro model of interfacial misfit dislocation [J]. Acta Materialia, 1999, 47(10): 3063-3068.
[21]Hong S I. Yield strength of a heavily drawn Cu-20%Nb filamentary micro composite [J]. Scripta Mater, 1998, 39: 1685-1691.
[22]Nye J F. Some geometrical relations in dislocation crystals [J]. Acta Metal Mater, 1953, 1: 153-162.
[23]Ashby M F. The deformation of plastically non-homogeneous materials [J]. Philos Mag, 1970, 21: 399-424.
[24]Biselli C, Morris D G. Microstructure and strength of Cu-Fe in-situ composites obtained from prealloyed Cu-Fe powders [J]. Acta Mater, 1994, 42: 163-176.
(Edited by LI Xiang-qun)
Received date: 2004-05-13; Accepted date: 2005-01-15
Correspondence: GE Ji-ping, Professor, PhD; Tel: +86-411-84106686; E- mail: ge@dlru.edu.cn