DOI: 10.11817/j.issn.1672-7207.2015.03.017
一种鲁棒的递推总体最小二乘无源定位算法
吴昊1,陈树新1,张衡阳1,张艺航1,倪娟2
(1. 空军工程大学 信息与导航学院,陕西 西安,710077;
2. 94303部队,山东 潍坊,261051)
摘要:针对机载无源定位易受异常误差影响的问题,提出一种基于角度信息的鲁棒递推总体最小二乘定位(RRTLS)算法。建立机载无源定位模型,得出递推总体最小二乘(RTLS)解。推导RTLS算法的加权形式,构建鲁棒总体最小二乘极值准则。在此基础上建立等价权函数,使得当出现异常误差时,算法能够自动识别异常误差,并利用降权、剔除奇异点的方式减小异常误差的影响。研究结果表明:随着误差的增大,RRTLS算法的影响函数绝对值减小,抗异常误差能力较强。仿真结果表明:存在异常误差时,递推最小二乘(RLS)和RTLS定位结果受到扭曲,而RRTLS算法能够获得理想的估值,具有较强的鲁棒性。
关键词:无源定位;鲁棒估计;总体最小二乘估计;影响函数
中图分类号:TN971 文献标志码:A 文章编号:1672-7207(2015)03-0886-08
Robust recursive total least squares passive location algorithm
WU Hao1, CHEN Shuxin1, ZHANG Hengyang1, ZHANG Yihang1, NI Juan2
(1. College of Information and Navigation, Air Force Engineering University, Xi’an 710077, China;
2. Unit 94303, Weifang 261051, China)
Abstract: To solve the problem that airborne passive location is susceptible to outliers, a robust recursive total least squares (RRTLS) airborne passive location algorithm was proposed based on the angle information. The airborne passive location model was established and the recursive total least squares(RTLS) solution was obtained. The RTLS solution was transformed into the weighted pattern, and robust TLS extreme value criterion was formulated. Then, the equivalent weight function was founded, which made the algorithm distinguish the outliers automatically, and the effects from outliers were reduced by the weight-reduction and the singular points elimination. The results show that with the increase of error, the value of the influence function in the RRTLS algorithm decreases, and the algorithm has high anti-outliers ability. When there are outliers, the results on the RLS and RTLS location are not reliable. On the other hand, the RRTLS algorithm performs an ideal estimation with good robustness.
Key words: passive location; robust estimation; total least squares estimation; influence function
机载单站无源定位因具有较高的军用和民用价值而得到广泛应用,其采用的定位方式主要有测角定位、到达时间定位、多普勒效应定位等[1-5]。一些测量环境较复杂的应用,角度信息也许是唯一能够得到的观测量,因此,研究单站测角无源定位具有重要的理论意义和实用价值。观测到目标位置的角度信息后,无源定位就转化为利用角度信息估计目标位置的问题。最小二乘(LS)估计是常用的定位算法,它计算简便、适用性强,但对于非线性的机载无源定位会导致估计结果不准确。Chan等[6]提出了一种两步加权的最小二乘定位算法,可以提高定位精度,但它是依据TDMA相关参数之间的关系推导的,且为批处理算法,依赖于初值的选取,不符合机载单站定位的要求。总体最小二乘算法(TLS)同时考虑了系数矩阵和观测向量中的误差,能够得到更为准确的定位结果[7]。Lim 等[8-9]将批处理TLS算法转化为递推形式(RTLS),提高了算法实时性,降低了运算复杂度,并应用到无源定位中。利用以上算法进行定位估计的前提是测量误差严格服从高斯或其他对称分布。然而在实际中,测量环境恶劣、观测站受到扰动等问题可能导致偏离正态分布的测量误差即异常误差的出现,它们往往呈非对称分布,会对定位结果造成较大影响[10]。对于异常数据的处理,通常有2种方式:一是对观测数据进行预处理,利用一定的准则将其剔除;二是采用鲁棒算法降低、消除异常误差的影响。前者往往需要预判观测值的统计特性,且预处理过程会对系统造成额外负担,实用性受到限制;后者精度较高,且可以合理利用观测数据的有用部分。为此本文作者根据广义M估计原理构建了鲁棒极值原则,推导出1种鲁棒的递推总体最小二乘定位算法,通过对异常数据进行降权的方式,有效解决了异常误差导致的定位结果不准确的问题。
1 定位模型及递推总体最小二乘解
图1所示为定位模型。如图1所示,假定定位目标T位于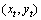 ,令飞机匀速直线运动并测向,
,令飞机匀速直线运动并测向,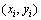 为第i个测向点的坐标,
为第i个测向点的坐标,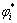 为飞机第i个测向点到辐射源的方位角。
为飞机第i个测向点到辐射源的方位角。
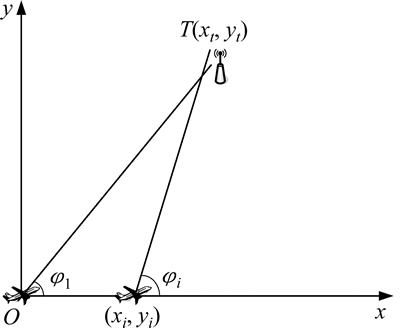
图1 定位模型
Fig. 1 Location model
于是有
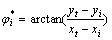 (1)
(1)
在实际中测得的角度总是存在误差的,即
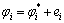 (2)
(2)
式中:ei为测角误差,一般假定其服从均值为0的高斯分布。为求解以上非线性方程,令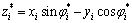 ,假定观测数据相互独立,n个测向点的测量方程可化为线性形式:
,假定观测数据相互独立,n个测向点的测量方程可化为线性形式:
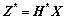 (3)
(3)
其中:
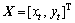 ,
,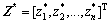 ;
;
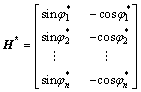
由式(2)可知观测向量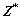 、系数矩阵
、系数矩阵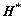 均受到噪声污染,即
均受到噪声污染,即
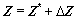 ,
, 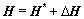 (4)
(4)
式中: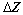 和
和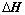 分别为观测向量和系数矩阵的误差矩阵。以上即为机载无源定位的二维观测方程,可以很容易推广至三维定位情况。式(3)最小二乘意义下的解为
分别为观测向量和系数矩阵的误差矩阵。以上即为机载无源定位的二维观测方程,可以很容易推广至三维定位情况。式(3)最小二乘意义下的解为
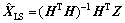 (5)
(5)
式(5)没有考虑H的扰动,估计结果有偏,为此同时考虑Z和H中干扰的影响,令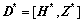 ,
, 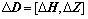 ,
,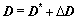 ,使方程组:
,使方程组:
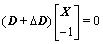 (6)
(6)
满足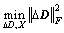 的
的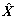 即为总体最小二乘解。其中
即为总体最小二乘解。其中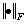 表示Frobenius范数。
表示Frobenius范数。
为求解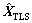 ,对D进行奇异值分解,得
,对D进行奇异值分解,得
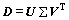 (7)
(7)
其中估计参量的个数为m,在本文二维定位中m=2。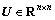 ,
,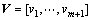 ,
,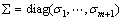 ,且
,且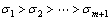 。
。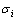 为矩阵D的奇异值。则得到目标的总体最小二乘解为[11]
为矩阵D的奇异值。则得到目标的总体最小二乘解为[11]
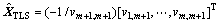 (8)
(8)
从以上讨论看出:TLS算法与式(5)相比,减小了由系数矩阵噪声引入的误差,可以得到更加精确估计结果。然而式(8)所示的批处理算法需要所有测量数据,且要进行奇异值分解和求逆运算,运算复杂度高、实时性差。于是将其推导为递推形式[7]:
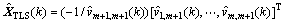 (9)
(9)
式中:
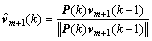 (10)
(10)
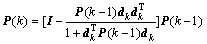 (11)
(11)
其中: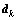 为
为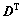 矩阵的第k列,
矩阵的第k列,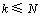 。
。
2 鲁棒递推总体最小二乘(RRTLS)算法
从式(2)和(4)看出:Z和H的扰动都来自测量数据的测角误差。如果扰动严格服从高斯分布,RTLS算法能够得到较准确的位置估计值。但在实际中,严格服从某一分布的测量数据是不存在的,一旦测量数据受到异常误差的污染,定位结果就会受到扭曲。为此引入污染分布[12]:
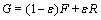 (12)
(12)
其中:F为主体分布;R为干扰分布;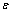 为污染率,表示污染的数据在所有测量数据中所占的比例。
为污染率,表示污染的数据在所有测量数据中所占的比例。
为了得到数据受到污染时的准确估计,本节首先推导RTLS算法的加权形式,然后利用广义M估计原理,识别并降低异常数据权值,从而减小异常误差对定位结果的影响。
2.1 加权递推总体最小二乘(WRTLS)算法
加权总体最小二乘准则可表示为[13]
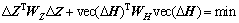 (13)
(13)
式中: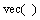 表示将矩阵元素按从左到右的顺序写为向量形式,
表示将矩阵元素按从左到右的顺序写为向量形式,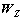 为
为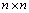 对角加权矩阵;
对角加权矩阵;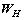 为
为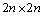 对角加权矩阵。
对角加权矩阵。
考虑到观测向量和系数矩阵的扰动均是由方位角噪声所引起的,且同一测量数据对观测向量和系数矩阵的影响是一致的,故对同一测量数据对应的观测值和系数矩阵值赋予同样的权值。即令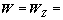
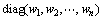 ,
,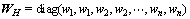 ,此时,
,此时,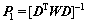 。记
。记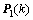 为k个数据得到的P1矩阵,即
为k个数据得到的P1矩阵,即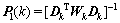 ,则可将其化简为
,则可将其化简为
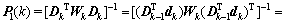
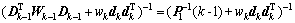 (14)
(14)
矩阵反演公式为
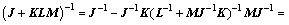
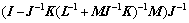 (15)
(15)
式中:J为非零方阵。
利用式(14)和(15)可将P1矩阵递推如下:
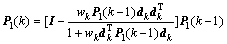 (16)
(16)
将式(10)中的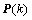 替换为
替换为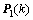 ,并利用式(9)和(16),即可求得WRTLS解。
,并利用式(9)和(16),即可求得WRTLS解。
2.2 鲁棒的递推总体最小二乘(RRTLS)算法
TLS准则是使Z和H中的误差平方和极小化,由于异常误差对误差平方和的影响较大,因而会造成估计结果偏离真实值。为此考虑极小化误差的某一函数,使其比二次函数增长速度慢,以得到更具鲁棒性的估值。估值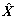 的误差方程为
的误差方程为
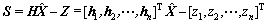 (17)
(17)
其中: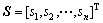 为残差向量。对于系数矩阵准确的情况,S仅来自观测向量Z,其M估计的极值函数为
为残差向量。对于系数矩阵准确的情况,S仅来自观测向量Z,其M估计的极值函数为
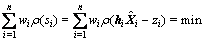 (18)
(18)
事实上,系数矩阵也是不准确的,所以,S中既有来自观测向量Z的部分,又有来自系数矩阵H的部分。故可将极值函数表示为
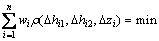 (19)
(19)
将式(19)对X求导并令为0,有
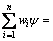
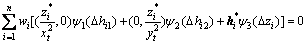 (20)
(20)
为了达到抵抗异常误差的目的,使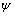 函数为有界函数,且当误差超过一定界限时,
函数为有界函数,且当误差超过一定界限时,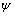 函数单调递减,这样误差对估值的影响就是有界的,从而减小异常误差对估值的影响。为此取权矩阵
函数单调递减,这样误差对估值的影响就是有界的,从而减小异常误差对估值的影响。为此取权矩阵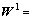
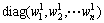 ,令
,令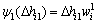 ,
,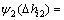
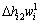 ,
,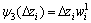 ,并令等价权因子
,并令等价权因子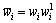 ,则式(20)可化为
,则式(20)可化为
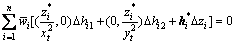 (21)
(21)
其中: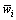 为有界、非增函数。
为有界、非增函数。
事实上,若取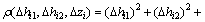
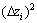 ,以上极值原则退化为式(19)表示的总体最小二乘极值原则,对其求导有
,以上极值原则退化为式(19)表示的总体最小二乘极值原则,对其求导有
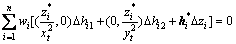 (22)
(22)
比较式(22)与式(21)可以看出鲁棒总体最小二乘估计和加权总体最小二乘估计的区别只是权矩阵不同,因此,鲁棒估计包容了总体最小二乘估计。将式(16)中先验权换为等价权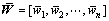 ,得到RRTLS算法为
,得到RRTLS算法为
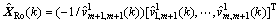 (23)
(23)
式中:Ro代表Robust,表示稳健或鲁棒。此时,
 (24)
(24)
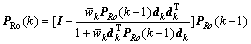 (25)
(25)
至此,将鲁棒估计问题转化为对等价权矩阵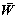 的设计问题。
的设计问题。
从以上讨论看出,RRTLS估计需要构造合适的等价权函数,使得当存在异常误差时权值减小或归零,以减小甚至消除异常误差对定位造成的不利影响。
考虑一阶Taylor展开:
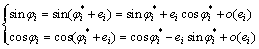 (26)
(26)
忽略测量误差的高阶项,由式(17)可知:

 (27)
(27)
从式(27)看出: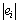 越大,
越大,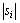 越大,也就是说残差绝对值大小反映了测量误差。因此,测量数据信息区间依据
越大,也就是说残差绝对值大小反映了测量误差。因此,测量数据信息区间依据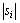 来划分,即取等价权因子
来划分,即取等价权因子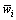 为
为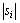 的函数。常用的等价权函数有Huber权函数、丹麦权函数、IGGⅢ权函数等[14]。其中,IGGⅢ权函数为
的函数。常用的等价权函数有Huber权函数、丹麦权函数、IGGⅢ权函数等[14]。其中,IGGⅢ权函数为
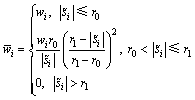 (28)
(28)
式中: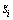 为标准化残差,
为标准化残差,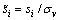 ,
,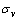 为残差的标准差;r0和r1为信息区间划分临界点。
为残差的标准差;r0和r1为信息区间划分临界点。
从式(28)知:IGGⅢ权函数将测量数据划分为可信域、怀疑域、淘汰域3个区域。权函数对可信域的数据采用原始权值;对怀疑域的数据降低权值,且权值随着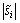 的增大而逐渐减小;将淘汰域的数据剔除,以消除大异常误差的影响。可信域保障了鲁棒估计的效率,其中的数据应当是测量数据的主体;可疑域综合考虑了估计的效率和可靠性,表示其中的数据出现异常但还可以利用;怀疑域和淘汰域共同体现了鲁棒估计的抗异常误差能力。而Huber权函数、丹麦权函数为两段权函数,仅有可信域和怀疑域,不能完全消除大异常误差的影响。
的增大而逐渐减小;将淘汰域的数据剔除,以消除大异常误差的影响。可信域保障了鲁棒估计的效率,其中的数据应当是测量数据的主体;可疑域综合考虑了估计的效率和可靠性,表示其中的数据出现异常但还可以利用;怀疑域和淘汰域共同体现了鲁棒估计的抗异常误差能力。而Huber权函数、丹麦权函数为两段权函数,仅有可信域和怀疑域,不能完全消除大异常误差的影响。
r0和r1反映了权函数对异常误差的敏感程度,一般来说,r0和r1的选取和异常误差出现的概率有关。测量环境越好,异常误差出现的概率越低,可将r0和r1取大,提高算法的效率;测量环境越恶劣,异常误差出现的概率越大,可将r0和r1取小,提高算法的可靠性。通常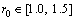 ,
,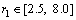 ,可根据应用环境的不同进行选取。
,可根据应用环境的不同进行选取。
需要注意的是,式(23)~(25)为实时递推算法,不能通过批处理算法的估计值计算残差。因此,在进行第i次递推时,先以第i-1次的RRTLS定位估计结果为初值进行一次RTLS估计,再利用该结果计算残差的估计值,即
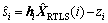 (29)
(29)
为保证残差估计值的准确,必要时还可对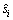 作迭代计算。
作迭代计算。
2.3 鲁棒性能分析
影响函数是统计量在相应母体分布下的一阶导数,反映了不同位置上的异常值对估值造成的相对影响[15]。其绝对值越小,抗异常误差能力越强。对于式(19)所示的准则,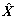 的影响函数为
的影响函数为
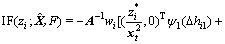
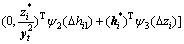 (30)
(30)
当主体分布确定后,A就是常数矩阵。于是得到RTLS算法和鲁棒RTLS算法的影响函数为

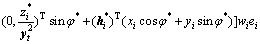 (31)
(31)
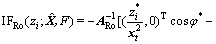
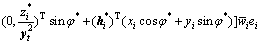 (32)
(32)
对于LS估计,由于 ,故其影响函数为[10]
,故其影响函数为[10]
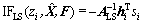 (33)
(33)
从式(30)看出:影响函数与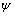 函数相关。对于TLS和LS算法,其
函数相关。对于TLS和LS算法,其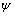 函数绝对值随测量误差的增大而增大,所以影响函数绝对值也增大,异常误差对其影响较大。而RRTLS算法的
函数绝对值随测量误差的增大而增大,所以影响函数绝对值也增大,异常误差对其影响较大。而RRTLS算法的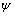 函数有界,其影响函数也是有界的,因此异常误差对算法的影响也是有界的,且当
函数有界,其影响函数也是有界的,因此异常误差对算法的影响也是有界的,且当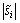 >
>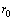 时,等价权函数随着误差的增大而递减,使影响函数绝对值减小直至为0,从而减小了异常误差对估计结果的影响。
时,等价权函数随着误差的增大而递减,使影响函数绝对值减小直至为0,从而减小了异常误差对估计结果的影响。
3 仿真分析
仿真参数设置如下:目标T(30 km, 180 km),递推初始值为(0, 0)。为研究方便,令飞机从原点出发,沿x正半轴等间距探测,探测间距为0.3 km。假定测量噪声主体服从均值为0,标准差为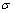 =0.6°的高斯分布。相对距离误差(
=0.6°的高斯分布。相对距离误差(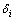 ):
):
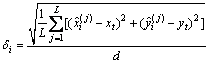 (34)
(34)
式中:d为目标T到飞机航迹的距离;L为仿真次数,这里令L=200,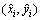 为目标位置的递推估计值。相对距离误差反映了算法定位精度。
为目标位置的递推估计值。相对距离误差反映了算法定位精度。
取先验权矩阵W为单位矩阵,鲁棒总体最小二乘估计的等价权函数为IGGⅢ,并令r0=1.5,r1=5。下面比较各个算法的性能。
3.1 仿真实验
仿真实验1:无异常误差。测量噪声严格服从均值为0,标准差为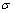 =0.6°的高斯分布。RLS算法、RTLS算法、XRTLS算法、RRTLS算法比较结果如图2所示。其中XRTLS算法是指利用
=0.6°的高斯分布。RLS算法、RTLS算法、XRTLS算法、RRTLS算法比较结果如图2所示。其中XRTLS算法是指利用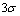 准则进行异常误差预处理后再利用RTLS法进行计算的方法。图3所示为各算法的标准化残差直方图。
准则进行异常误差预处理后再利用RTLS法进行计算的方法。图3所示为各算法的标准化残差直方图。
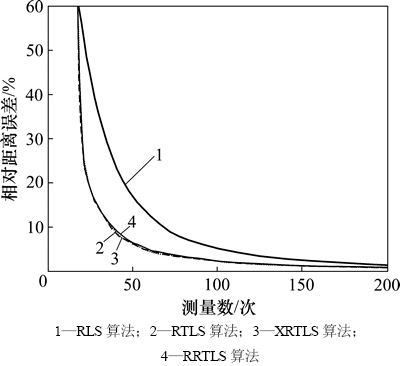
图2 算法性能比较(无异常误差)
Fig. 2 Performance of various algorithms (no outliers)
仿真实验2:有异常误差干扰。数据主体的测量噪声服从均值为0,标准差为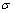 =0.6°的高斯分布,异常误差设置如表1所示。
=0.6°的高斯分布,异常误差设置如表1所示。
表1 异常误差设定
Table 1 Outliers setting

图4和图5分别为上述条件下的算法性能曲线和标准化残差直方图。
仿真实验3:污染率与算法鲁棒性的关系。主体数据服从均值为0,标准差为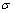 =0.6°的高斯分布,设定异常误差大小为
=0.6°的高斯分布,设定异常误差大小为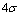 。不同污染率下算法性能比较如图6所示。
。不同污染率下算法性能比较如图6所示。
3.2 仿真结果分析
1) 由图2可见:不存在异常误差时,4种算法均能逐渐趋于收敛,其中RTLS算法、XRTLS算法和RRTLS算法的收敛速度和定位精度明显优于RLS算法,具有更高的估值效率。总体来看,由于测量噪声严格服从高斯分布,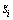 超过r0的概率较低,故RTLS算法、XRTLS算法和RRTLS算法的收敛速度和定位精度基本一致。但递推初期RTLS算法略优于XRTLS和RRTLS算法,这是由于此时RRTLS算法的估值离真实值较远,利用式(29)估计的
超过r0的概率较低,故RTLS算法、XRTLS算法和RRTLS算法的收敛速度和定位精度基本一致。但递推初期RTLS算法略优于XRTLS和RRTLS算法,这是由于此时RRTLS算法的估值离真实值较远,利用式(29)估计的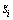 存在偏差,可能导致估值效率受到影响。从图3可见:4种算法的后验标准化残差直方图基本符合高斯分布,并且标准化残差均分布在(-3, 3)内,估值较为理想。
存在偏差,可能导致估值效率受到影响。从图3可见:4种算法的后验标准化残差直方图基本符合高斯分布,并且标准化残差均分布在(-3, 3)内,估值较为理想。
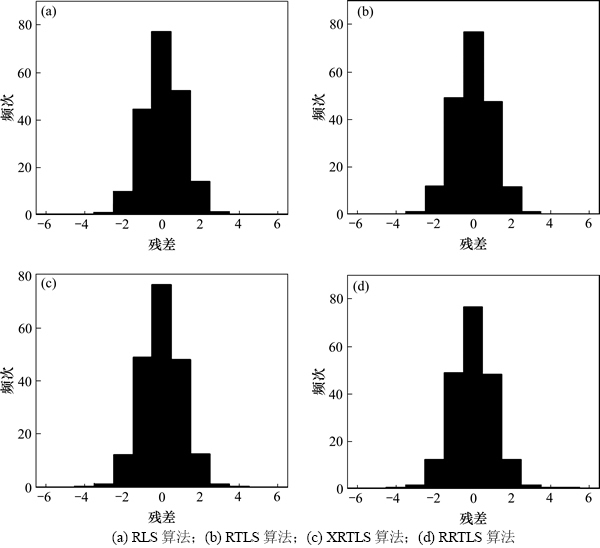
图3 标准化残差直方图(无异常误差)
Fig. 3 Standard residual histograms (no outliers)
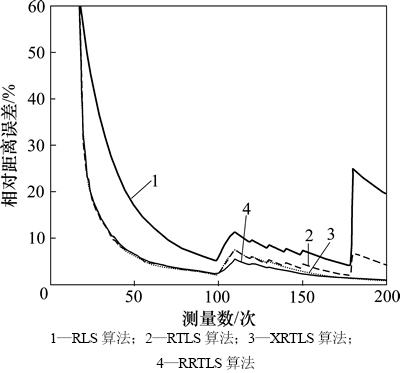
图4 算法性能比较(有异常误差)
Fig. 4 Performance of various algorithms (outliers)
2) 由图4可见:当测量数据存在异常误差时,RLS和RTLS算法定位结果受到不同程度的影响,均未达到定位精度需求;XRTLS算法虽然能够识别较大的异常误差,但对于连续的小异常误差则判别能力较差,而RRTLS算法仍然能够较快收敛。从图5可看出:异常误差使4种算法的残差变大,但RRTLS算法的后验标准化残差分布在(-6, 3)范围内,仍基本符合标准高斯分布,可信度较高,而RLS算法、RTLS算法的标准化残差明显偏离高斯分布,且平均最大残差分别达到了59.3和52.4,算法受到质疑。
3) 当飞机受到小的扰动(101~110测量点),4种算法的定位精度均受到影响,但RRTLS算法受到的影响较小。这是因为RRTLS算法通过残差估计值识别出该部分测量数据存在异常,进行降权处理,从而降低了异常误差的干扰。而采用“硬判决”方式的XRTLS算法则对这部分异常误差的识别能力较差;同时XRTLS算法可能将有效数据判别为异常数据,影响定位效率,而RRTLS算法采取对可疑数据降权的方式,同时考虑了算法的效率和可靠性。在120,130,140和150测量点,由于降低了异常误差的影响,RRTLS算法曲线更为平缓。当出现大异常误差(180测量点)时,RLS算法和RTLS算法定位结果明显受到扭曲,而RRTLS算法将该处数据的权值降为0,消除了大异常误差对估值的影响。
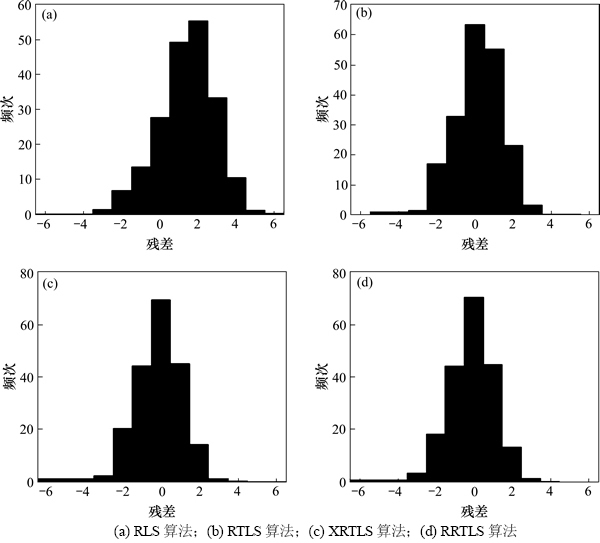
图5 标准化残差直方图(有异常误差)
Fig. 5 Standard residual histogram (outliers)
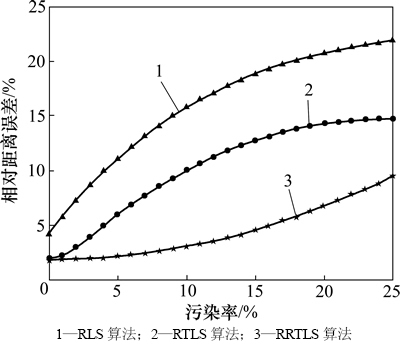
图6 不同污染率下算法性能比较
Fig. 6 Performance of various algorithms in different pollution rate
4) 由图6可见:3种算法的定位精度随着污染率的增加而降低。其中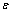 >4%时,RTLS算法的相对距离误差超过5%,而RRTLS算法在
>4%时,RTLS算法的相对距离误差超过5%,而RRTLS算法在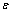 =13%时仍然能够满足定位精度需求,鲁棒性较强。当然,污染分布不同,算法的鲁棒性能也会不同。
=13%时仍然能够满足定位精度需求,鲁棒性较强。当然,污染分布不同,算法的鲁棒性能也会不同。
4 结论
1) 机载单站无源定位易受到异常误差的干扰。同时考虑定位模型中观测向量和系数矩阵扰动的影响,推导了一种鲁棒的递推总体最小二乘定位算法。该算法运算复杂度低,所需存储空间小,能够满足机载无源定位的实时性需求。它通过标准化残差绝对值自动识别异常误差,利用等价权函数对其进行降权,从而减小或消除异常测量数据对定位精度和收敛速度的影响。从影响函数可以看出,RRTLS算法具有较强的鲁棒性。仿真结果表明,RRTLS算法能够有效抵抗异常误差的干扰,优于传统抗异常误差方法,且具有较高的估值效率,可以提供更为真实的辐射源位置信息。
2) 算法初期,残差估计的不准确可能导致RRTLS算法估值效率略低,下一步将针对这一问题对算法进行改进,同时进一步讨论噪声、定位初值等因素对算法鲁棒性的影响。
参考文献:
[1] 刘学, 焦淑红, 孙亮. 基于改进的平方根中心差分卡尔曼滤波的单站无源定位算法[J]. 吉林大学学报(工学版), 2011, 41(6): 1777-1782.
LIU Xue, JIAO Shuhong, SUN Liang. Improved central difference Kalman filter for single observer passive location[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1777-1782.
[2] WANG Zhi, LUO Jian, ZHANG Xiaoping. A novel location-penalized maximum likelihood estimator for bearing-only target localization[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6166-6181.
[3] SHEN Junyang, Molisch A F, Salmi J. Accurate passive location estimation using TOA measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(6): 2182-2192.
[4] Amar A, Weiss J. Localization of narrowband radio emitters based on Doppler frequency shift[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5500-5508.
[5] Deming R, Schindler J, Perlovsky L. Multi-target/multi-sensor tracking using only range and Doppler measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 593-611.
[6] Chan Y, Ho K. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915.
[7] Golub G H, van Loan C F. An analysis of total least-squares problem[J]. SIAM J Number Anal, 1980, 17(6): 883-893.
[8] Lim J S, Choi N, Sung K M. Robust recursive TLS (Total Least Square) method using regularized UDU decomposed for FNN (Feedforward Neural Network) training[J]. Lecture Notes in Computer Science, 2005, 3496(1): 578-584.
[9] 吴昊, 陈树新, 张衡阳. 基于递推总体最小二乘的机载单站无源定位算法[J]. 空军工程大学学报(自然科学版), 2013, 14(1): 62-65.
WU Hao, CHEN Shuxin, ZHANG Hengyang. Recursive total least square-based airborne single-observer passive location algorithm[J]. Journal of Air Force Engineering University (Natural Science Edition), 2013, 14(1): 62-65.
[10] 杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006: 95-98.
YANG Yuanxi. Adaptive navigation and kinematic positioning[M]. Beijing: Surveying and Mapping Press, 2006: 95-98.
[11] Bertrand A, Moonen M. Low-complexity distributed total least squares estimation in Ad hoc sensor networks[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4321-4333.
[12] Tukey J W. A Survey of sampling from contaminated distributions in contributions to probability and statistics[M]. Stanford Calif: Stanford University Press, 1960: 14-25.
[13] Schaffrin B, Wieser A. On weighted total least-squares adjustment for linear regression[J]. Journal of Geodesy, 2008, 87(7): 415-421.
[14] 颜伟, 宋林滔, 余娟, 等. 基于权函数的电网参数分区辨识与估计方法[J]. 电力系统自动化, 2011, 35(5): 25-30.
YAN Wei, SONG Lintao, YU Juan, et al. A divisional identification and estimation method of network parameter errors based on weight function[J]. Automation of Electric Power Systems, 2011, 35(5): 25-30.
[15] Sehirlioglu A K. Influence functions for the moment estimators[J]. Journal of Science, 2010, 23(1): 7-11.
(编辑 陈爱华)
收稿日期:2014-05-10;修回日期:2014-08-19
基金项目(Foundation item):国家自然科学基金资助项目(61202490) (Project(61202490) supported by the National Natural Science Foundation of China)
通信作者:吴昊,博士研究生,从事无源定位跟踪算法的研究;E-mail: wuhaostudy@163.com