基于模拟退火算法的低温余热发电系统参数优化
王志奇1, 2,周乃君1 ,郭静1,王晓元1
(1. 中南大学 能源科学与工程学院,湖南 长沙,410083;
2. 湘潭大学 机械工程学院,湖南 湘潭,410005)
摘要:为提高低温余热发电系统的综合性能,以单位发电量所需换热面积为目标函数,采用模拟退火算法对ORC系统的参数进行优化。研究结果表明:当热源温度和流量分别为120 ℃与62 kg/s,蒸发器内最小传热温差为10 ℃时,蒸发器内的最佳压力和流速分别为0.615 MPa与1.23 m/s;冷凝器内的最佳压力和流速分别为0.102 MPa与1.37 m/s;与传统算法相比,优化结果使单位发电量所需换热面积减少23%。随着热源温度的升高,最优目标函数值先降低后升高,在热源温度为200 ℃时达到最低值;综合考虑目标函数值及系统输出净功,蒸发器内合适的最小传热温差为15 ℃。
关键词:参数优化;模拟退火;余热发电
中图分类号:TK11 文献标志码:A 文章编号:1672-7207(2012)01-0366-06
Parametric optimization of low-temperature waste heat power generation system by simulated annealing algorithm
WANG Zhi-qi1, 2, ZHOU Nai-jun1, GUO Jing1, WANG Xiao-yuan1
(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;
2. Institute of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)
Abstract: An optimized mathematical model was established to improve the performance of low-temperature waste heat power generation system. The ratio of the total heat exchanger area to net power output was used as the objective function and it was optimized using the simulated annealing algorithm. The heat resource is the flue gas when the mass flow is 62 kg/s and temperature is 120 ℃. When the minimum temperature difference between evaporator and flue gas is 10℃, the results show that the optimal pressure and velocity in evaporator are 0.615 MPa and 1.23 m/s, respectively. And the optimal pressure and velocity in condenser are 0.102 MPa and 1.37 m/s, respectively. The ratio of the total heat exchanger area to net power output decreases by 23% compared with conventional method. The optimal value of objective function reaches the minimum when the heat source temperature is 200 ℃. In order to get lower value of objective function and higher net power output, the proper temperature difference of evaporator is 15 ℃.
Key words: parametric optimization; simulated annealing algorithm; waste heat power generation
随着化石能源消耗量的不断攀升,能源已成为全世界共同关注的一个重大问题。然而,工业生产中大量低品位余热(温度低于230 ℃)都直接排放到环境中,造成了巨大的能量浪费。回收这部分低温余热可以缓解能源危机,达到节能减排的目的。有机朗肯循环(ORC)是回收低温余热的有效技术途径[1-3]。近年来,国内外许多学者对ORC系统进行了大量研究。Maizza等[4]比较了不同种类有机工质的效率,得出 R123具有较好性能的结论。Lee等[5]对ORC系统进行了热力分析,认为工质的蒸发温度和冷凝温度将对系统的经济性产生重要影响;Saleh等[6]指出随着工质临界温度的增加,循环的热效率增加。魏东红等[7]研究了环境温度对系统性能的影响,结果表明,环境温度对系统输出功率产生较大影响,环境温度波动时系统偏离额定功率最高可达30%。Dai等[8]研究了蒸发压力对ORC系统发电量的影响,指出ORC系统处于最佳蒸发压力时,系统产生的净输出功率最大。总的来看,针对ORC系统的研究工作主要集中在:工质的选择、循环方式的优化以及单一参数(如冷凝温度、汽轮机进口压力等)对系统性能的影响等方面。然而,这些研究工作并没有对如何组织多个参数使系统性能达到最优这一问题进行研究。模拟退火算法是一种高效的优化算法,能避免传统优化算法在寻优过程中只得到局部最优解的缺点,因而在很多工程优化问题中得到应 用[9-11]。本文作者采用模拟退火算法,以单位发电量所需的换热面积为目标函数,对低温余热发电系统中的蒸发压力、冷凝压力以及介质在换热器内的流速等参数进行优化,以获得ORC系统的最佳运行时这些参数的大小,为回收低温烟气余热提供理论依据。
1 理论分析
ORC系统利用低温余热加热循环工质,产生的高温高压蒸气推动膨胀机对外做功,从而达到余热动力利用的目的。系统由蒸发器、透平机、冷凝器以及泵组成,其系统构成及理论循环的温熵(T-S)图分别见图1(a)和(b)(图中,1~7表示不同状态点,具体是:1表示冷凝器出口;2表示泵出口;3表示蒸发器出口;3′为工质的饱和点;4表示膨胀机口;5为热源入口;6为饱和点对应的热源温度;7为热源出口温度;4S表示等熵膨胀时的出口状态)。
在循环中系统所需的工质流量为:
 (1)
(1)
式中:mg为烟气流量,kg/s;h为比焓,kJ/kg;下标2, 3, 5, 7为T-S图上不同状态点。
汽轮机输出的功:
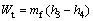 (2)
(2)
 (3)
(3)
式中:h4,is为工质在透平机内绝热等熵膨胀时的出口焓,kJ/kg;ηt为透平机的内效率,%。

图1 ORC系统构成及T-S曲线
Fig.1 Sketch map of ORC system and T-S curve
ORC系统中换热器内的压降可根据下式计算:
 (4)
(4)
式中:λ为阻力因数;l为换热管长度,m;D为换热管内径,m;ρ为管内介质密度,kg/m3;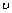 为管内介质流速,m/s。
为管内介质流速,m/s。
工质泵及水泵消耗的功率分别为[12]:
 (5)
(5)
 (6)
(6)
式中:p为压强,Pa;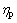 为泵的绝热效率,%;下标“f”表示工质;“e”表示蒸发器;“c”表示冷凝器;“w”表示水。
为泵的绝热效率,%;下标“f”表示工质;“e”表示蒸发器;“c”表示冷凝器;“w”表示水。
ORC系统的净输出功率为:
 (7)
(7)
系统中换热器传热面积的计算式为:
 (8)
(8)
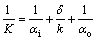 (9)
(9)
式中:Q为换热量,W;K为综合传热系数,W/(m2·K);?t为传热温差,℃; 和
和 分别为管内和管外对流换热系数,W/(m2·K);δ为管壁厚度,m;k为管壁热导率,W/(m·K)。
分别为管内和管外对流换热系数,W/(m2·K);δ为管壁厚度,m;k为管壁热导率,W/(m·K)。
烟气侧的换热系数可由下式计算得到[13]:
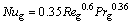 (10)
(10)
式中:Nu为努塞尔数;Re为雷诺数;Pr为普兰特数。
处于单相区时,管内换热系数采用Petukhov关系式[14]:
 (11)
(11)
 (12)
(12)
式中:f为管内湍流流动阻力因数。
对于水平管内两相流对流换热系数,采用Varme Atlas关系式计算[15]:
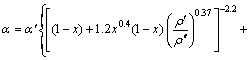
 (13)
(13)
式中:x为工质的干度;r为工质的蒸发潜热,kJ/kg;上标“′”表示饱和液相;“″”表示饱和气相。
管外凝结换热系数为[16]:
 (14)
(14)
式中:kf为工质的热导率,W/(m·K);μf为工质的黏度,Pa·s;tb为管壁温度,℃。
系统的循环热效率为:
 (15)
(15)
当蒸发器与热源间的最小传热温差的位置位于工质进口时,ORC系统从烟气获得的热量最多。由此,定义系统的热回收率为蒸发器吸热量除以蒸发器的最大吸热量。假定比热为常数时,系统的热回收率可表示为:
 (16)
(16)
式中:tmin为蒸发器与热源间的最小传热温差,℃。
2 优化模型及优化方法
2.1 优化模型
(1) 目标函数
在低温余热回收中,系统所需的换热面积大,使得换热器在系统总投资中所占的比例高。为提高系统综合性能、缩短投资回收期,以单位净输出功率所需的换热面积为目标函数。
 (17)
(17)
(2) 设计变量
蒸发器与冷凝器内的压力是影响系统输出电能的重要参数。此外,蒸发器及冷凝器内介质的流速将影响换热性能和介质压降,进而影响换热器面积及泵所消耗的功率。因此,本文确定的ORC系统设计变量为:
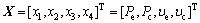 (18)
(18)
(3) 约束函数
为避免环境中的空气进入系统中,冷凝器内的压力应大于大气压力,则:
x2≥0.101
根据ORC系统的循环过程可知蒸发压力应高于冷凝压力:
x1-x2>0
蒸发压力应小于工质的临界压力:
x1<pL
管内介质的流速应大于零:
x3>0, x4>0
2.2 优化方法
模拟退火方法是一种模拟金属退火过程随机搜索方法。模拟退火算法采用Metropolis 准则来决定一个新解是接受还是舍弃。其具体描述如下:先给定粒子相对位置表征的初始状态i,该状态的固体能量为Ei。然后使随机选取的某个粒子位移随机地产生一个微小变化,得到一个新的状态j,该状态的能量Ej。如果Ej<Ei,则接受新状态j为当前状态。否则,考虑到热运动的影响,根据固体处于该状态的几率来判断。
模拟退火算法在求解优化问题过程中,将内能E模拟为目标函数值f;温度T演化成控制参数t。在算法的每一步,随机产生一个新的候选解,如果这个新解使目标函数减小,则可以接受;否则要以指数概率的形式来决定它是否接受。
对于一个新解,被接受的概率为:
 (19)
(19)
式中:i和j为模拟退火过程中不同状态点。
模拟退火算法过程中,当在给定邻域结构后,模拟退火过程从一个状态到另一个状态不断的随机“游动”。这个过程可用马尔可夫(Marvob)链来描述。当温度t为一确定值时,2个状态的转移概率定义如下:
 (20)
(20)
式中:G为从i到j的产生概率,%;|E|为状态集合中的状态个数。
由初始解x0和控制参数初值t0开始,对当前解重复“产生新解—计算目标函数差—判断是否接受—接受或舍弃”的迭代, 并逐步衰减t值。算法终止时的当前解即为所得最优解。模拟退火算法的迭代过程如图2所示。
3 结果与分析
ORC系统中,热源为120 ℃的烟气,流量为 62 kg/s;系统采用R123为循环工质,蒸发器及冷凝器中的最小传热温差分别为10 ℃和5 ℃,环境温度为20 ℃;汽轮机和泵的效率为0.8,工质以饱和蒸汽进入汽轮机膨胀做功。本文利用Matlab语言编写模拟退火算法程序,对ORC系统进行参数优化,结果如表1所示。

图2 模拟退火算法流程
Fig.2 Procedure of simulated annealing algorithm
只考虑蒸发压力变化时,以系统最大输出功率为目标函数,利用模拟退火算法所得的优化结果如表1中工况1所示。从表1可以看出:系统的最大输出功率为334 kW,这与文献[14]中的结果一致。当以单位输出净功所需换热面积为目标函数时(工况2),冷凝器内的最佳压力和流速分别为0.102 MPa与0.74 m/s;蒸发器内的压力和流速分别为0.615 MPa与0.98 m/s。与传统算法相比,ORC系统的净功虽然降至269 kW,然而总的传热面积降低39.1%,目标函数值降低23.1%。因此,通过参数优化,可以大幅提高单位换热面积上的发电量,从而提高系统的性能。
热源温度及蒸发器内最小传热温差对ORC系统的影响如图3~6所示。
表1 模拟退火算法优化结果
Table 1 Result of simulated annealing algorithm


图3 不同热源温度时目标函数值
Fig.3 Temperature of heat source versus value of objective function

图4 不同热源温度时系统热效率及热回收率
Fig.4 Temperature of heat source versus system efficiency and ratio of heat recovery
由图3可见:随着热源温度的提高,目标函数值显著减少。当热源温度为100 ℃时目标函数值为7.6,温度升至180 ℃时目标函数值为3.2,目标函数值降低58%,这表明热源温度对系统性能产生巨大的影响。
此外,随着热源温度的进一步升高,目标函数值将随之增加。当蒸发器内最小传热温差为10 ℃时,200 ℃下的目标函数值最低,为2.9。此时,蒸发器内的压力和流速分别为2.01 MPa与0.73 m/s;冷凝器内的压力和流速分别为0.102 MPa与1.45 m/s。
这主要是由于:一方面,随着热源温度的增加,系统的热效率及热回收率提高,如图4所示,使得系统从热源中吸收更多的热量并转化为有用功,导致输出净功增加;另一方面,热回收率的增加使得烟气出口温度降低,导致蒸发器两侧的传热温差降低,使得换热面积增大。当换热面积增加比例高于净功增加比例时,目标函数值增大,系统的综合性能降低。因此,当蒸发器内最小传热温差一定时,热源温度过低或过高都可能导致目标函数值较高。
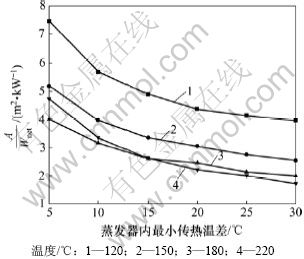
图5 不同蒸发器最小传热温差时的目标函数值
Fig.5 Minimum temperature difference in evaporator versus value of objective function

图6 不同蒸发器最小传热温差时系统输出净功
Fig.6 Minimum temperature difference in evaporator versus system net power
图5所示为不同热源温度下目标函数值随蒸发器内工质与热源间最小传热温差的变化趋势。从图5可以看出:随着最小传热温差的增加,系统的目标函数值降低。热源温度为120 ℃下,最小传热温差从5 ℃增加至30 ℃时,目标函数值从7.4降到3.9。此外,当最小传热温差大于15 ℃时,热源温度越高,目标函数值越小。
虽然随着最小传热温差的增加目标函数值降低,然而系统的输出净功也将减少,如图6所示。由图6可知:热源温度为120 ℃下,最小传热温差为5 ℃和30 ℃所对应的系统输出净功为332 kW与110 kW。因此,当热源温度一定时,蒸发器内最小传热温差过高将导致系统的输出净功过低,降低系统的总效益。
结合图5可知:当最小传热温差从5 ℃变化至15 ℃时,目标函数值下降幅度较高。而最小传热温差高于15 ℃时,目标函数值的变化比较平缓。热源温度为120 ℃与180 ℃下,最小传热温差从5 ℃变化至15 ℃时,目标函数值分别降低34.3%和34.7%,输出净功分别降低36.1%和30.8%;最小传热温差从15 ℃变化至25 ℃时,目标函数值降低15.1%和19.2%,输出净功分别降低32.5%和24.1%。因此,为获得较低的目标函数值以及较高的输出功率,蒸发器内合适的最小传热温差为15 ℃。
4 结论
(1) 热源温度为120 ℃,蒸发器内最小传热温差为10 ℃时,蒸发器内最佳压力和流速分别为0.615 MPa与1.23 m/s;冷凝器内的最佳压力和流速分别为0.102 MPa与1.37 m/s;与传统分析方法相比,优化结果使系统单位输出净功所需换热面积降低23%。
(2) 蒸发器内最小传热温差为10 ℃时,随着热源温度的升高,目标函数值先降低后升高,200 ℃下的目标函数值最低。
(3) 随着蒸发器内最小传热温差的升高,目标函数值及系统输出净功降低;综合考虑目标函数值及系统输出净功,蒸发器内合适的最小传热温差为15 ℃。
参考文献:
[1] Larjola J. Electricity from industrial waste heat using high-speed organic Rankine cycle (ORC)[J]. International Journal of Production Economics, 1995, 41(3): 227-235.
[2] Schuster A, Karellas S, Kakaras E, et al. Energetic and economic investigation of organic Rankine cycle applications[J]. Applied Thermal Engineering, 2009, 29(7): 1809-1817.
[3] 顾伟, 翁一武, 曹广益, 等. 低温热能发电的研究现状和发展趋势[J]. 热能动力工程, 2007, 22(2): 115-120.
GU Wei, WENG Yi-wu, CAO Guang-yi, et al. The lastest research findings concerning low-temperature heat energy-based power generation and its development trend[J]. Journal of Engineering for Thermal Energy and Power, 2007, 22(2): 115-120.
[4] Maizza V, Maizza A. Unconventional working fluids in organic Rankine-cycles for waste energy recovery systems[J]. Applied Thermal Engineering, 2001, 21(3): 381-390.
[5] Lee M, Tien D, Shao C. Thermophysical capability of ozone-safe working fluids for an organic Rankine cycle system[J]. Heat Recovery Systems and CHP, 1993, 13(5): 409-418.
[6] Saleh B, Koglbauer G, Martin W, et al. Working fluids for low-temperature organic Rankine cycles[J]. Energy, 2007, 32(7): 1210-1221.
[7] 魏东红, 陆震, 鲁雪生, 等. 废热源驱动的有机朗肯循环系统变工况性能分析[J]. 上海交通大学学报, 2006, 40(8): 1398-1392.
WEI Dong-hong, LU Zhen, LU Xue-sheng, et al. Performances analysis of the organic Rankine cycle driven by exhaust under disturbance conditions[J]. Journal of Shanghai Jiaotong University, 2006, 40(8): 1398-1402.
[8] DAI Yi-ping, WANG Jiang-feng, GAO Lin. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery[J]. Energy Conversion and Management, 2009, 50(3): 576-582.
[9] 邹恩, 李祥飞, 刘耦耕, 等. 最优模糊神经网络参数的设计—混沌模拟退火学习法[J]. 中南大学学报: 自然科学版, 2004, 35(3): 443-447.
ZOU En, LI Xiang-fei, LIU Ou-geng, et al. Optimization de sign for parameters of FNN: Learning algorithm of chaos simulated annealing[J]. Journal of Central South University: Science and Technology, 2004, 35(3): 443-447.
[10] 周龙, 牟怿, 尤新革. 模拟退火算法在粮虫图像分割中的应用[J]. 华中科技大学学报: 自然科学版, 2010, 38(5): 72-74.
ZHOU Long, MOU Yi, YOU Xin-ge. Application of simulated annealing algorithm in image segmentation of pests in stored grain[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2010, 38(5): 72-74.
[11] 徐林, 吴效明, 张燕儒. 基于模拟退火算法的AEI-CPR外作用力优化[J]. 华南理工大学学报: 自然科学版, 2009, 37(12): 95-99.
XU Lin, WU Xiao-ming, ZHANG Yan-ru. Optimization of external force of AEI-cardiopulmonary resuscitation based on simulated annealing algorithm[J]. Journal of South China University of Technology: Natural Science Edition, 2009, 37(12): 95-99.
[12] Madhawa Hettiarachchia H.D, Golubovica M, Woreka W M. Optimum design criteria for an organic Rankine cycle using low-temperature geothermal heat sources[J]. Energy, 2007, 32(9): 1698-1706.
[13] 杨世铭, 陶文铨. 传热学[M]. 3版. 北京: 高等教育出版社, 2003: 177.
YANG Shi-ming, TAO Wen-quan. Heat transfer[M]. 3rd ed. Beijing: High Education Press, 2003: 177.
[14] Lakew A A, Bolland O. Working fluids for low-temperature heat source[J]. Applied Thermal Engineering, 2010, 30(10): 1-7.
[15] Jensen J M. Dynamic modeling of thermo-fluid systems with focus on evaporators for refrigeration[D]. Denmark: Technical University of Denmark. Department of Mechanical Engineering, 2003: 1-173.
[16] 钱颂文. 换热器设计手册[M]. 北京: 化学工业出版社, 2002: 67-68.
QIAN Song-wen. Heat exchanger design handbook[M]. Beijing: Chemical Industry Press, 2002: 67-68.
(编辑 杨幼平)
收稿日期:2010-12-10;修回日期:2011-02-28
基金项目:湖南省科技厅计划项目(2009GK2009);科技部中小企业创新基金资助项目(08C26224302178)
通信作者:王志奇(1979-),男,湖南湘潭人,博士研究生,讲师,从事工业过程节能研究;电话:13789306990;E-mail: wangzhiqi@xtu.edu.cn