Phase-field simulation of dendritic sidebranching induced by thermal noise
ZHU Chang-sheng(朱昌盛)1, 2, WANG Zhi-ping(王智平)1, JING Tao(荆 涛)3, LIU Bai-cheng(柳百成)3
(1. CAD Center, Lanzhou University of Technology, Lanzhou 730050, China;
2. State Key Laboratory of Gansu New Nonferrous Metal Materials,Lanzhou University of Technology, Lanzhou 730050, China;
3. Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China)
Abstract: The influence of undercooling and noise magnitude on dendritic sidebranching during crystal growth was investigated by simulation of a phase-field model which incorporates thermal noise. It is shown that, the sidebranching is not influenced with inclusion of the nonconserved noise, therefore, in order to save the computational costs it is often neglected; while conserved noise drives the morphological instability and is dominant origin of sidebranching. The dependence of temperature field on magnitude of thermal noise is apparent, when Fu gets an appropriate value, noise can induce sidebranching but not influence the dendritic tip operating state. In the small undercooled melt, the thermal diffusion layer collected around the dendrite is thick, which suppresses the growth of its sidebranching and makes the dendrite take on the morphology of no sidebranching, but when the undercooling is great, the thermal diffusion layer is thin, which is advantageous to the growth of the sidebranching and the dendrite presents the morphology of the developed sidebranching.
Key words: phase-field method; undercooling; thermal noise; dendritic sidebranching; numerical simulation CLC number: TG248; TG244
Document code: A
1 INTRODUCTION
Dendrites are intricate patterns that make up the microstructure of many important commercial alloys[1]. They develop a complex shape due to the emission of secondary branches behind the growing tips of primary branches. This side-branching mechanism requires some continuous source of noise at the tip. Therefore, thermal noise, originating from microscopic scale fluctuations inherent in bulk matter, is the most natural and quantifiable candidate to consider[2, 3]. Barber et al[4] studied the evolution of time-dependent deformations of the needle crystal (Ivantsov) solution of the two-dimensional symmetric model of solidification in the limit of small Pèclet number within a WKB approximation. The amplitude of a localized wave packet grows exponentially as z1/4, where z is the distance measured from the tip along the symmetry axis of the dendrite. Brener and Temkin[5] considered anisotropic needle crystals in three dimensions and concluded that experimentally observed sidebranching could be explained by considering noise of a thermal origin. The growth of the sidebranching amplitude was found to behave exponentially as a function of z2/5, which is faster than z1/4 dependence obtained in the axisymmetric case[6]. The sidebranching wavelength was found to be a function of z1/5, very similar to that obtained in the [CM(22]axisymmetric case. Recently, many studies on side-[CM)]branching with a phase-field model have been carried out[7-11]. They obtained good quantitative agreement between the computed sidebranching amplitude as a function of distance to the tip and the prediction of the linear WKB theory for anisotropic crystals in two dimensions[2, 7]. In this paper, dendritic sidebranching during crystal growth is investigated by simulation of a phase-field model which incorporates thermal noise of microscopic origin. Some key problems in modeling and numerical computation of this kind of advanced microstructure simulation method are solved, the dendrite growth behavior under the different conditions are finely described, and mechanism of the dendrite growth in the undercooled melt is discussed.
2 MATHEMATICAL MODEL AND NUMERICAL ISSUES
Methods to incorporate thermal noise in the phase-field model have been developed by Karma and Rappel[1]. Although some previous phase-field simulations have obtained dendritic sidebranchings that resemble those observed in experiments[12-14], those sidebranchings are generated by either numerical noise or by randomly driving the tip. In the model of Karma and Rapple, thermal noise is incorporated in a thermodynamically consistent manner using the Langevid formalism. The nonconserved noise and conserved noise are added to the phase equation and the energy conservation equation respectively in the following manner:
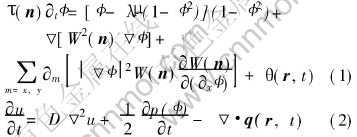
The dimensionless temperature u is defined as (T-TM)/(L/cp), where TM, L and cp are the melting temperature, latent and specific heat at constant pressure, respectively. D is the thermal diffusivity, λ is coupling constant, both τ and W are functions of the interfacial normal n in order to account for anisotropic surface energy and kinetics, respectively:

θ and q stand for the thermal noise vector, obeying Gaussian distribution with variances respectively:
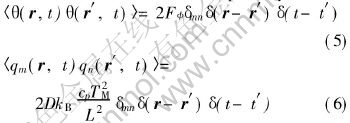
where kB is the Boltzmann constant and δ is the delta function. Using W0 as a length scale and τ0 as a time scale, all dimensional variables are cast into their dimensionless form as r/W0→r, t/τ→t, Dτ0/W20→D, τθ→θ, qτ0/W0→q, the dimensionless variance of the thermal noise vector are then given by
〈θ(r, t)θ(r′, t)〉= 2Fδmnδ(r-r′)δ(t-t′)(7)
〈qm(r, t)qn(r′, t)〉= 2DFuδmnδ(r-r′)δ(t-t′)(8)
where Fu is the magnitude of the thermal noise defined as
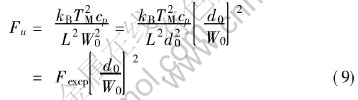
The phase field Eqn.(1) is solved using Euler algorithm, while ADI algorithm is applied for the heat Eqn.(2). The space step is selected as Δx≤W0, the time step is specified in such a way that  for keeping stable under time-step iterations. In order to save the computational cost, the computation region is extended according to the increasing dendritic scale.
for keeping stable under time-step iterations. In order to save the computational cost, the computation region is extended according to the increasing dendritic scale.
For an initial nucleus of the radius r0, when x2+y2≤r2, =1, u=0; when x2+y2>r2, =-1, u=-Δ. Where x and y are the coordinate axes, u is dimensionless temperature.
The Zero-Neumann boundary conditions for and u are imposed at the boundaries of the computational domain[15].
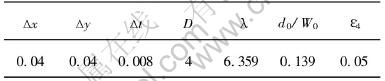
All phase-field parameters are given in Table 1.
Table 1 Computational parameters used in simulation
3 NUMERICAL RESULTS AND DISCUSSION
3.1 Dendrite morphology and temperature field with no noise
Without consideration of noise, the morphology of no-sidebranching is obtained by reducing W0 gradually to eliminate numerical error, so that it can be compared with the dendrite morphology where noise was introduced. Fig.1 (a) shows the morphological interfaces plotted every 5000 iterations at different growth time. From the figure, it can be found that the dendrite keeps smooth all the time during the course of development and no sidebranching appears. The corresponding temperature field of dendritic pattern 1 shown in Fig.1(a) is presented in Fig.1(b). From the figure, we can see that the higher temperature of solid fall gradually to the initial temperature of liquid by the thermal diffusion layer. The temperature gradient between dendritic tips is bigger, while the roots is the smallest.
3.2 Effect of undercooling on equiaxed dendritic growth pattern
The undercooling has great effects on both dendritic nucleation and growth. The lower the undercooling, the smaller the nucleation rate, that is, in the same volume melt, each nucleus possesses more free space to grow. On the other hand, with the decrease of undercooling, the growth velocity slows down, and dendrite needs more time to grow. It is on the assumption that thermal magnitude is constant (Fu=2×10-4). Fig.2(a) shows the equiaxed dendrite without sidebranching obtained by the simulation of dimensionless temperature u=0.2 and growth time t=60h. Fig.2(c) presents the equiaxed dendrite with the developed sidebranching under high dimensionless undercool-ing of u=0.65 and growth time t=15h. The corresponding temperature distributions near equiaxed dendrite shown in Figs.2(a) and (c) are presented in Figs.2(b) and (d) respectively. From the figures, it can be found that under the low undercooling, the thermal diffusion layer surrounding the equiaxed dendrite is thicker than that of the high undercooling. The latent heat given out during the equiaxed dendrite growing releases through the thermal diffusion layer, the thermal diffusion length is DT/Vc. Because the growth velocity under low undercooling is slower than that of high undercooling, so the thermal diffusion length under low undercooling melt is longer than that of high undercool-
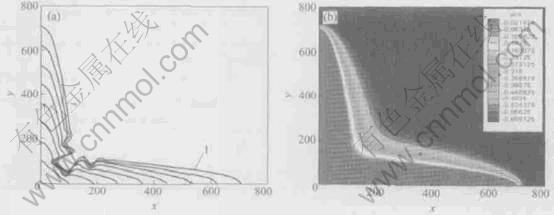
Fig.1 Dendritic pattern interface plotted every 5000 iterations(no noise, Δ=0.65) (a) and temperature field at time of dendritic pattern 1 growth in
Fig.1(a) (b)

Fig.2 Dendritic pattern and temperature field
ing melt, which makes the equiaxed dendrite surrounded by thicker thermal diffusion layer. Thermal diffusion layer baffles the release of latent heat and restricts the perturbation of interface, as a result, side-branches are suppressed, so the equiaxed dendrite takes on the morphology of no sidebranching. Moreover under high undercooling, thin thermal diffusion layer facilitates the release of latent heat and promotes the development of sidebranching, therefore, the equiaxed dendrite presents the morphology of highly developed sidebranching.
3.3 Effect of magnitude of thermal noise on sidebraching
The influence of thermal amplitude value on the simulation results is obvious. Fig.3(c) shows the temperature field of dendrite growth at some time with noise amplitude Fu=10-4. From the figure, it can be found that the inclusion of thermal noise does not change the law of temperature field distribution, but makes temperature field fluctuate randomly and the highest temperature is beyond 0 and the lowest is under initial undercooling, which disagrees with the actual law of temperature field distribution. With the increase of the noise level Fu, the fluctuations of temperature field enhance. The curves 1 and 2 shown in Fig.3(a) represent dendrite patterns of no noise and Fu=10-4 at time t=20h respectively. From the figures, we can see that with the noise included, durative fluctuations are formed near the interface, and side-branches appear behind the dendrite tip from several wavelength, but the phase fields of dendritic tip in two cases superpose, which indicates that the noise enhances the emergence of sidebranching, but it doesnt influence the steady state of the dendrite tip. As shown in Fig.3(b), the dendritic tip of pattern 1 with no noise and the dendritic tip of pattern 2 with Fu=10-3 at time t=20h dont superpose, and the vertical branch velocity outgrows the horizontal branch velocity, which indicates that great noise will disturb the steady state. Therefore, the value of Fu must be tried again and again.
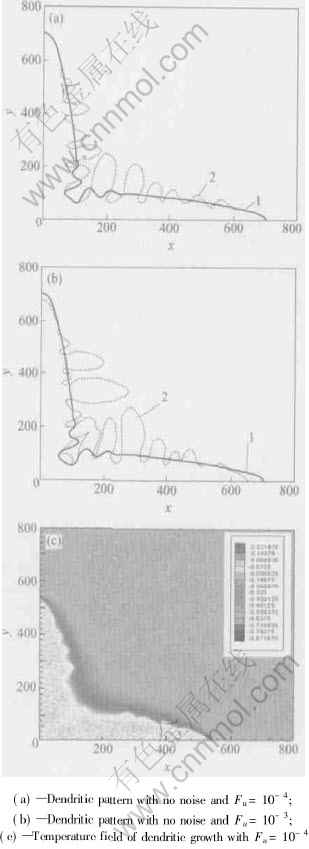
Fig.3 Dendritic pattern and temperature field
3.4 Effect of conserved noise and nonconserved noise on sidebranching
On the assumption that noise level Fu is assigned to a constant, simulation is carried out with both noises (conserved noise q and nonconserved noise θ) and only the conserved noise q. The result shows that sidebranching characteristics are identical in the two cases at the same iterative times, which indicates that the conserved noise which is the main origin of the sidebranching can make dendritic sides unstable and while the nonconserved noises contribute little to the sidebranching. This can be explained as follows: when growth velocity is small, the conserved noise drives long-wavelength interface fluctuations that become amplified to a macroscopic scale by the morphological instability on the sides of dendrites[2]. Contrarily, the nonconserved noise drives short-wavelength fluctuations that are damped and do not affect sidebranching[2]. Consequently, the nonconserved noise is ignored in actual computations, the random numbers per site at each time step will be reduced from 3 to 2. In this way, computational costs will be saved and computational efficiency will be improved, but the simulation results are not influenced.
4 CONCLUSIONS
1) In the phase-field simulation of dendritic sidebranching, different undercooling and magnitude of thermal noise lead to different dendrite sidebranching behaviors.
2) When the undercooling is small, the thick thermal diffusion layer is collected around the equiaxed dendritic, which suppresses the growth of its sidebranching and makes the equiaxed dendritic take on the morphology of no sidebranching.
3) In the great undercooled melt, the thermal diffusion layer is thin, which is advantageous to the growth of the sidebranching and the equiaxed dendritic presents the morphology of the developed sidebranching.
4) The conserved noise drives the morphological instability on the sides of dendrites and is dominant origin of sidebranching.
5) The sidebranching is unaffected with inclusion of the nonconserved noise, so it can be negligible from the point of view of computational saving for long simulation runs.
6) The magnitude of thermal noise influences temperature field obviously, when appropriate value is assigned to Fu , noise can enhance the emergence of sidebranching but not influence the tip operating state.
REFERENCES
[1]Huang S C, Glicksman M E. Fundamentals of dendritic solidification-I. Steady-state tip growth[J]. Acta Metallurgica, 1981, 29: 701-715.
[2]Karma A, Rappel W J. Phase-field model of dendritic sidebranching with thermal noise[J]. Phys Rev E, 1999, 60(4): 3164-3624.
[3]Dougherty A, Kaplan P D, Gollub J P. Development of side branching in dendritic crystal growth[J]. Phys Rev Lett, 1987, 58(16): 1652-1655.
[4]Barber M N, Barbieri A, Langer J S. Dynamics of dendritic sidebranching in the two-dimensional symmetric model of solidification[J]. Phys Rev A, 1987, 36(7): 3340-3349.
[5]Brener E, Temkin D. Three-dimensional dendritic growth[J]. Physica A, 1999, 263(4): 338-344.
[6]Langer J S. Dendtitic sidebranching in the three-dimensional symmetric model in the presence of noise[J]. Phys Rev A, 1987, 36(7): 3350-3358.
[7]Kobayasi R. Modeling and numerical simulation of the dendritic growth[J]. Physica D, 1993, 63: 410-423.
[8]Li Q, Beckermann C. Evolution of the sidebranch structure in free dendritic growth[J]. Acta Mater, 1999, 47(8): 2345-2356.
[9]Karma A, Rappel W J. Phase field method for computationally efficient modeling of solidification with arbitrary interface kinetics[J]. Phys Rev E, 1996, 53(4): R3017-3020.
[10]Kobayashi R. Modeling and numerical simulation of dendritic crystal growth[J]. Journal of Computation Physics, 1999, 154(1): 410-415.
[11]Pieters R, Langer J S. Noise-driven sidebranching in the boundary-layer model of dendritic solidification[J]. Phys Rev Lett,1986, 56(18): 1948-1951.
[12]Murray B T, Wheeler A A, Glicksman M E. Simulation of experimentally observed dendritic growth behavior using phase-field model[J]. J Cryst Growth, 1995, 154: 386-400.
[13]Tong X, Beckermann C, Karma A, et al. Phase-field simulation of dendritic crystal growth in a forced flow[J]. Phys Rev E, 2001, 63: 1-16.
[14]Gonzálet-Cinca R, Ramírez-Piscina L. Sidebranching induced by external noise in solutal dendritic growth[J]. Phys Rev E, 2000, 63: 1-9.
[15]YU Yan-mei, YANG Gen-cang, ZHAO Da-wen, et al. Effects of temperature boundary conditions on equiaxed dendritic growth in phase-field simulations of binary alloy[J ]. Trans Nonferrous Met Soc China, 2002, 12(6): 1063-1068.
(Edited by YUAN Sai-qian)
Foundation item: Project (59990470; 50005011) supported by the National Natural Science Foundation of China
Received date: 2004-06-12; Accepted date: 2004-08-26
Correspondence: ZHU Chang-sheng, PhD; Tel: +86-931-2756739; E-mail: zhucs@lut.cn