Analytical solution for coupled diffusion of three-components liquid in porous pellet
XU Zeng-he(徐曾和)1, WANG Jin-xia(王锦霞)2
(1. School of Resource and Civil Engineering, Northeastern University,Shenyang 110004, China;
2. School of Materials and Metallurgy, Northeastern University, Shenyang 110004, China)
Abstract: The coupled three-components liquid diffusion within a porous pellet was investigated. The coupled diffusion model was given according to irreversible thermodynamics, and the rigorous solutions of the model subject to the homogeneous boundary conditions of the first kind are derived by employing Hankel transform technique and the standard technique resolving ordinary differential system. The method can also be used to solve the other coupled diffusion problems within a pellet with different kinds of boundary conditions. Then the case computations were conducted. The calculation results show that the effect of interdiffussion on the concentration of components depends upon the diffusion time strongly, after a long diffusion period, a very small cross diffusion coefficient will induce the observable change of concentration profile, and that, when the cross coefficients are close to 5%-7% of the main coefficients, the significant effect of coupled diffusion on the concentration profiles of components is observed. The case computations also show that interdiffussion can induce non-monotonous concentration profiles. So, for the diffusion taking place within ternary system, the concentration profiles obtained by the analysis of interdiffussion can be very different from that obtained by the equivalent binary system analysis method.
Key words: ternary system; coupled diffusion; analytical solution; irreversible thermodynamics CLC number: TQ021.4
Document code: A
1 INTRODUCTION
Diffusion in liquid in presence of multi-components is common in engineering practice, for example, the separation operation as liquid-liquid extraction, gas absorption and distillation. Many phenomena in nature, even in organism bodies, are dealt with, such as the diffusion of air in rivers and salt in blood. Because the diffusion in ternary system is more common, much attention has been, recently, paid to it. Van den Berg et al[1] reviewed in detail the developments in membrane separation. Nagata et al[2] investigated the diffusion in ternary system associated with metallurgy processes. Palicia et al[3] studied the diffusion of three-component liquids in food. However, the new developments on the diffusion in ternary systems are still found seldom in literatures. Bochet et al[4] proposed a method for calculating interdiffusion coefficients by inverse numerical computation. Oleg et al[5] suggested that the available experimental data on the diffusion in ternary system should be verified by Onsagers reciprocal relations. So far, it is the common method that the diffusion in ternary system are studied as the equivalent binary system[6], owing to the complexity of the interdiffusion problems in theory and especially in experiment in ternary system. The diffusion of three-component fluids in porous media is also common. Xin et al[7] reported the effective diffusivities of gas in porous media. Most of gas-solid heterogeneous noncatalytic reactions in metallurgy are associated with the intraparticle diffusion of ternary gases. Although the metallurgy kinetics is a mature field, the intraparticle coupled diffusion of ternary gases is ignored completely in the study of the kinetics of a single particle so far. For example, Muchi et al[8] reported the kinetics of a single particle associated with reaction system of aA(g)+bB(s)=cC(g)+dD(s) without considering the intraparticle coupled diffusion of ternary gases. Patisson et al[9], Eddings et al[10], Hindmarsh et al[11] also ignored the interaction between gaseous reactant and product in the investigation of the overall rate of a single pellet. Likewise, at the reactor level, the diffusion of tri-components fluids is often neglected. For example, in spite of the presence of ternary gases, Winkelman et al[12] , Boaventura et al[13] neglected the coupled effect between the gaseous reactant and gas product in their investigation on the mass transfer within reactor.
According to irreversible thermodynamics[14], the diffusion flux of the ith species depends on not only the gradient of chemical potential itself but also that of all others in the system. In this paper, the coupled diffusion of three-components liquid in a porous pellet is studied. First, the model of coupled diffusion is given, then, the exact solution of the problem is derived, and finally the impacts of the interaction of diffusion between different components are discussed.
2 MODEL OF COUPLED DIFFUSION IN PELLET AND ITS ANALYTICAL SOLUTION
Consider the mass transfer in a porous pellet in presence of three gas components and in absence of convection and chemical reaction. If solvent is taken as the third species, the mass fluxes for two solutes according to irreversible thermodynamics are
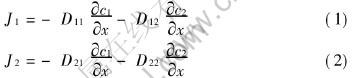
Here, the assumptions that the diffusions in ternary system take place under the isothermal condition, and that diffusion coefficients are independent of solution concentrations, i.e. they are constants, have been employed. In Eqns.(1) and (2), D11 and D22 are main diffusion coefficients of components 1 and 2, respectively, which represent the effects of the concentration gradient of specific components on the diffusions themselves. D12 and D21 are cross diffusion coefficients, which represent the interactions of the diffusion between component 1 and 2.
To a pellet, the mass conservations in spherical coordinate without reaction and convection are

Eqns.(3) and (4) are coupled and can be solved after initial and boundary conditions are specified. The asymptotical solutions of Eqn.(3) and (4) have been obtained by using perturbation method in Ref.[15]. However, the rigorous solutions for Eqns.(3) and (4) exist. Here, we devote to the derivation of rigorous solutions of Eqns.(3) and (4).
The initial conditions are
t=0, c1(r, 0)=c10; c2(r, 0)=c20(5)
where subscript 10 denotes component 1 at t=0; 20 denotes component 2 at the same time. Boundary conditions on the surface of pellet are
c1(R, t)=0; c2(R, t)=0(6)
where subscripts 1 and 2 denote components 1 and 2, respectively.
Because of the symmetry, the fluxes of the mass of components 1 and 2 are always zero at the center of the pellet, that means
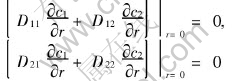
Then Eqn.(7) can be derived easily from the above two equations
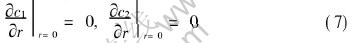
Eqns.(3)-(7) are the coupled diffusion model with homogeneous boundary condition of the first kind.
Introducing new functions in the form
w1(r, t)=rc1(r, t)(8)
w2(r, t)=rc2(r, t)(8′)
By differentiating Eqns.(8) and (8′), the following formula can be derived easily

Substitution of Eqns.(9), (9′) and Eqns.(10), (10′) into Eqns.(3) and (4) yields
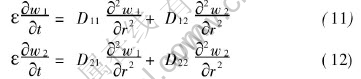
From Eqns.(8) and (8′) and Eqns.(5)-(7), the initial and boundary conditions for w1, w2 can be derived
t=0 w1(r, 0)=rc10;
w2(r, 0)=rc20 0≤r〈R(13)
r=R w1(R)=0; w2(R)=0(14)
r=0 w1(0)=0; w2(0)=0(15)
Eqns.(11)-(15) are basically the same equations as Eqns.(3)-(7), but, now, they are in the rectangular coordinate system with variables w1 and w2. The coupled problems (11)-(15) can be resolved analytically.
We employ first Hankel transform technique to remove the partial derivatives with respect to space variable[16]. It is well known from Refs.[16, 17] that the eigenvalue problem corresponding to Eqns.(11)-(15) is

The eigenfunctions and the positive eigenvalue roots satisfying problem (Ⅰ) can be derived easily

Inversion formula[16] is
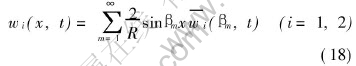
Multiplying both sides of Eqns.(11) and (12) by sinβmx, then integrating over the region R, the we get
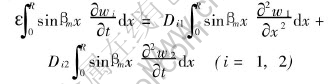
The integral on the right-hand side of above equations can be evaluated by making use of Greens theorem[18], the application of the theorem yields
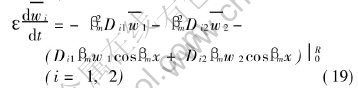
The third term on the right-hand side of Eqn.(19) is evaluated by boundary conditions of variables wi of Eqns.(14) and (15), and the boundary conditions of eigenfunctions (x,βm)=sinβmx. Obviously, the third term on the right-hand side of Eqn.(19) is zero. So, it leads to
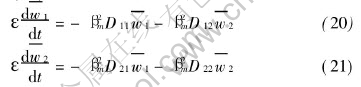
The integral transform of the initial conditions become
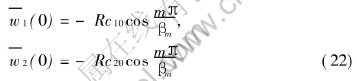
All the partial derivatives with respect to space variables have been now removed from the diffusion equation system (11)-(15) and the original partial differential equations have been reduced to ordinary differential equation system (20)-(22). In the process of integral transformation, the boundary conditions have been employed, therefore they have been incorporated into the resultant solutions.
The analytical solutions of the ordinary equation system (20) and (21) subject to the initial condition given as Eqns.(22) can be obtained easily by using the standard technique resolving ordinary differential system, which can be found in any text books on ordinary differential equations, so the procedure of evaluation are not repeated here, only resultant solutions are written as
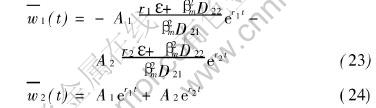
where
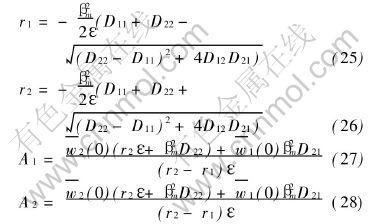
For any problems of ternary system which make sense in theory and practice, the main diffusion coefficients D11 and D22 are larger than the cross diffusion coefficients D12 and D21. It can be observed from Eqns.(28) and (29) that both r1 and r2 are less than zero. In fact, it is the necessary condition for series (29) and (30) to be convergent.
Substitution of Eqns.(23) and (24) into Eqn.(18) yields
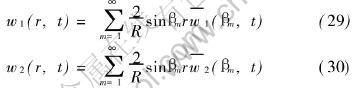
The analytical solutions of equation system (3) and (4) can now be written as
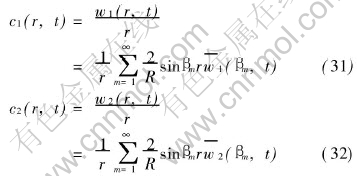
The solutions obtained are derived under the homogeneous boundary conditions of the first kind. The rigorous solutions of Eqns.(3) and (4) subject to the other boundary conditions are also obtained by employed successively Hankel transformation and the standard technique resolving ordinary differential system.
Because of the symmetry, the conditions at the center of pellet are always the same, so, only the boundary conditions on the outer boundary of pellet can be changed.
For the non-homogeneous boundary condition of the first kind, the eigenvalue problem, eigenfunctions and eigenvalue roots, integral transform and inversion formula still remain unchanged. However, the ordinary differential equation system after removing the partial differential with respect to space variable by Hankel transformation is the ordinary differential system with non-homogeneous terms on the right side of the equation system
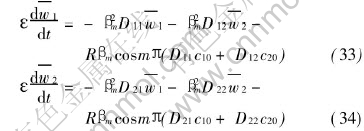
The standard technique resolving ordinary differential equation system can be still utilized to obtain the analytical solutions of the equation systems (33) and (34).
The boundary conditions of the second kind at outer boundary of pellet are
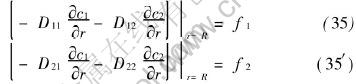
The boundary conditions of c1 and c2 equivalent to (35) and (35′) can be derived easily as follows
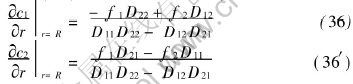
Obviously, homogeneous boundary conditions of second kind at the outer boundary of pellet have been included in Eqns.(35), (35′) and (36), (36′) as special case. The eigenvalue problem corresponding to Eqns.(11) and (12) and boundary condition (36) and (36′) is[16, 17]

Eigenfunctions and the positive eigenroots satisfying eigenvalue problem (Ⅱ) are[16, 17]

Multiplying both sides of Eqns.(11) and (12) by sinβmx, and repeating the same procedure, the exact solutions of Eqns.(11) and (12) subject to boundary conditions (36) and (36′) can be obtained, from which the corresponding exact solutions of Eqns.(3) and (4) can be derived.
3 CASE COMPUTATIONS AND DISCUSSION
Investigate the effects of cross diffusion on the concentration of components through cases computation of the diffusion of ternary system H2O-NaCl-KCl in a pellet, in which H2O is taken as solvent, NaCl and KCl as solutes 1 and 2, respectively. The diffusion coefficients, D11=3.40×10-6cm2/s, D12=-0.02×10-6cm2/s, D21=0.32×10-6cm2/s, D22=4.58×10-6cm2/s, the porosity of pellet, ε=0.575, are taken out of Ref.[12]. The initial concentrations of NaCl and KCl, c10=0.25mol/L, c20=0.25mol/L are also taken out of Ref.[12]. Put the radius of pellet R=1cm, and the concentration of NaCl and KCl in main fluid out of pellet are always zero, i.e. c1|r=R=0, c2|r=R=0.
Fig.1 shows the evolutions of concentration profile of components 1 and 2 with time. Since the main diffusion coefficients of components dominate their diffusion, and D11〈D22, the diffusion of component 1 is slower than that of component 2. Because both components 1 and 2 move outwards under specified initial and boundary conditions here, the concentration of component 1 is higher than that of component 2.
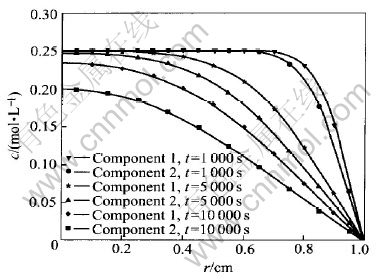
Fig.1 Evolution of concentration profile of components 1 and 2 with time
Fig.2 shows the interaction of the diffusion between components 1 and 2. To component 1, the effect of cross diffusion on its concentration is very small, since the cross diffusion coefficient is three orders lower than the main diffusion coefficient. As to component 2, the ratio of cross diffusion coefficient to its main diffusion coefficient D21/D22 is 7%. So the effects of cross diffusion are observable. Cross diffusion coefficient D12〈0 indicates that the diffusion of component 1 is going to be slowed down because of the presence of the concentration gradient of component 2, i.e. the motion of component 1 is going to be slower and its concentration will be higher than that in absence of component 2. Since D21>0, according to the same reason, the motion of component 2 will be faster and its concentration will be lower than that in absence of component 1.
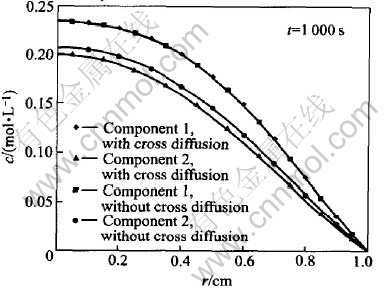
Fig.2 Interaction of diffusion between components 1 and 2
Fig.3 shows the concentrations of components 1 and 2 schematically. Except the calculation is conducted at t=50000s, the other parameters and coefficients employed in the calculation of Fig.3 are the same as those in Fig.2. For component 1, the concentration difference obtained by coupled analysis and non-coupled analysis, which is so small to be distinguished in Fig.2, can be observed in Fig.3 now. For component 2, the maximal relative concentration difference between interdiffusion and non-coupled diffusion reaches almost 100%. The comparison of Figs.2 and 3 shows that the effect of interdiffusion depends upon the diffusion time obviously.
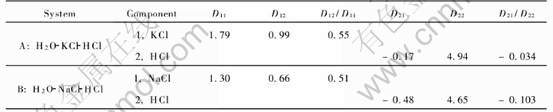
Fig.4 shows the computation results schematically for the two different ternary systems. The coefficients and parameters used in computation are listed in Table 1, which are taken from Ref.[12]. The initial concentrations of components 1 and 2, which are also taken from Ref.[12] are 0.3mol/L and 0.2mol/L, respectively. The ratio of main diffusion coefficients of component 1 in system B to the component 1 in system A (DB11/DA11) is 0.726, where superscripts B and A denote H2O-NaCl-HCl system and H2O-KCl-HCl system, respectively. The ratios of their cross diffusion coefficients to main diffusion coefficients themselves are 50% and
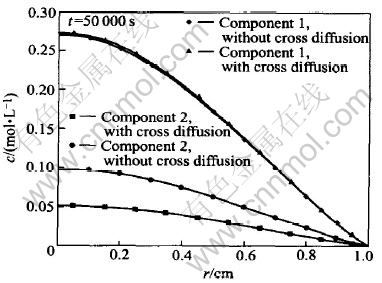
Fig.3 Effect of long diffusion period on coupled diffusion

Fig.4 Coupled diffusion in two different ternary systems
55%, respectively. This means the effect of cross diffusion on the diffusion of component 1 in H2O-KCl-HCl system and that in H2O-NaCl-HCl system are approximately equal. Therefore, the concentration difference of component 1 between H2O-KCl-HCl system and H2O-NaCl-HCl system mainly induced by the difference of their main diffusion coefficients. Since the main diffusion coefficient of component 1 in H2O-KCl-HCl system is greater than that in H2O-NaCl-HCl system, the motion of [CM(22]component 1 in H2O-KCl-HCl system is faster and[CM)]
Table 1 Parameters of two different ternary systems
its concentration is lower.
The ratio of the main diffusion coefficient of component 2 in B to that in A (DB22/DA22) is 0.94. To component 2 in H2O-KCl-HCl system, the ratio of cross diffusion coefficient to main diffusion coefficients is -3.4%, while in H2O-NaCl-HCl system the same ratio is -10.3%. These facts mean that the concentration concentration difference of component 2 HCl in different systems is induced mainly by interdiffusion. The diffusion of component 2 HCl in system H2O-KCl-HCl and in system H2O-NaCl-HCl system will be both slowed down owing to the presence of the other component, since the cross diffusion coefficients of component 2 in different system are both negative. Because the cross diffusion coefficient of component 2 HCl in system H2O-KCl-HCl is less than that in H2O-NaCl-HCl system, according to the above discussion, component 2 in H2O-KCl-HCl system migrated more quickly than in H2O-NaCl-HCl system, and the concentration is less than that in H2O-NaCl-HCl system.
If no other component is in present, the concentration difference of component 2 in different systems should not observed, since the main diffusion coefficients of component 2 in these two systems are approximately equal. Therefore, the obvious concentration difference of component 2 in systems, which is shown schematically in Fig.4, should be attributed to the interaction of diffusion between different components. This computation result implicates once again that the interaction of diffusion between the two components in ternary system cant be neglected if the ratio of cross diffusion coefficients to main diffusion coefficients are close to 10%.
Fig.5(a) shows the computation results for component 1 schematically, the ratio of cross diffusion coefficient to the main diffusion coefficient is only 0.59% there. Component 2 has hardly any impact on the migration of component 1, unless the cross diffusion coefficient is amplified. The impact of cross diffusion on the migration of component 2 is shown in Fig.5(b). For component 2, the ratio of cross diffusion coefficient to main diffusion coefficient reaches 7%, the obvious impact of component 1 on the motion of component 2 can be observed. Because D21 and D22 are the same in sign, the diffusion of component 2 is speeded up due to the presence of component 1, the motion of component 2 will be faster and its concentration will be lower with the increase of D21. If the sign of D21 is changed, the migration of component 2 will be slowed down due to the presence of component 1 (see curve 4 in Fig.5(b)).
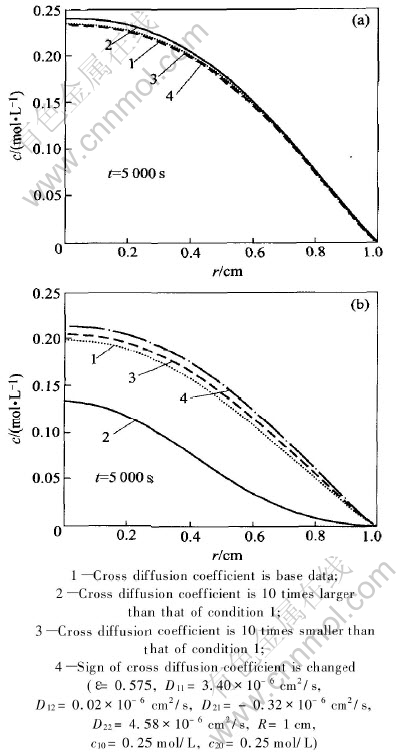
Fig.5 Effects of cross diffusion on components 1(a) and 2(b)
The investigation on the three-components fluids diffusion by applying the equivalent binary system method indicates that the components profiles are always monotonous[19, 20]. The above case computation of interdiffusion also exhibits the monotonous concentrations profiles of components 1 and 2. It seems that the difference between the interdiffusion and the non-coupled diffusion is only in magnitude and not in property. In order to further discuss the possible difference between coupled diffusion and non-coupled diffusion, we re-calculate the concentration profiles of components 1 and 2. Except that the computation is conducted at t=1000s, the other parameters and coefficients employed in the calculation in Fig.6, are the same as those in Fig.4.
It can be known from Table 1 that the cross diffusion coefficients D12 of components 1 in sys-
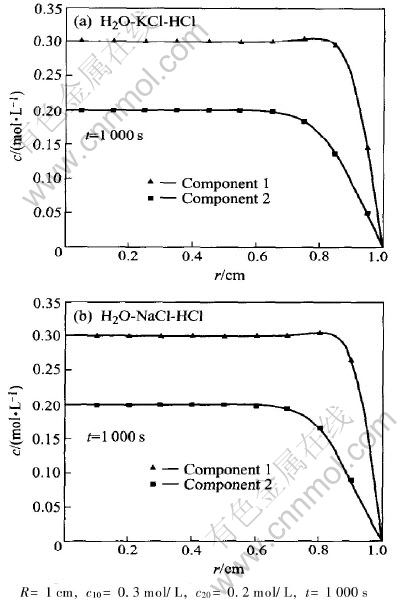
Fig.6 Effect of long diffusion period on coupled diffusion of systems A(a) and B(b)
tem A and B are both positive, and the main diffusion coefficients of components 1 in system A and B are much lower than those of components 2 in system A and B. The former means that component 2 will promote component 1 to move more quickly outward out of pellet than it does in absence of coupled diffusion effect, while the latter means that component 2 will move more quickly than component 1 will do, and the concentration of components 2 will be much lower than that of component 1. It can be observed from Fig.6 that at the place close to the surface of pellet, the motion of component 2 steeps up suddenly, and their concentration drop dramatically. It will inevitably lead to the more quick motion of component 1. Because the main diffusion coefficients of components 1 is not enough large, they can't migrate in time out of pellet, and pile up in the local region, therefore, their concentrations increase in the local region. Noting that the region where component 1 piles up is roughly equal to the region where the concentration of component 2 drops suddenly. It is agree to the effect of interdiffusion on the migration of components.
The calculation results in Fig.6 indicate that the concentration profiles obtained by the analysis of interdiffussion can be very different from those obtained by the equivalent binary system analysis. This also indicates once more that the effect of interdiffussion on the concentration of components depends upon the diffusion time strongly.
4 CONCLUSIONS
1) On irreversible thermodynamics, the coupled partial differential system describing three-component liquids diffusions within a porous pellet is presented. The rigorous solutions of the problems are derived by employed Hankel transform technique and the standard technique resolving ordinary differential system successively.
2) The impact of coupled diffusion on the components migration and concentrations change can't be neglected when the cross coefficients are close to 5%-7% of the main diffusion coefficient.
3) The effect of interdiffussion on the concentration of components depends upon the diffusion time strongly.
4) The concentration profiles obtained by the analysis of interdiffussion can be very different from those obtained by the equivalent binary system analysis.
In this paper, the exact solution of the coupled diffusion problems within a porous pellet with boundary conditions of the third kind are not given, because the mass transfer within boundary layer of a pellet is not discussed. That attributes mainly to the three-component liquids diffusing in the boundary layer of porous media is a big problem itself. So, for coupled diffusion problems in porous media, it is a ambiguous problem itself what is the correct boundary condition of the third kind.
REFERENCES
[1]Van den Berg G B, Smoblers C A. Diffusional phenomena in membrane separation processes [J]. Journal of Membrane Science, 1992, 73: 103.
[2]Nagata K, Goto K S. Transport coefficients of ions and interdiffusivities in multicomponent ionic solution of CaO-SiO2-Al2O3 at 1500℃ [J]. Journal of Electrochemical Society, 1976, 123(12): 1814-1820.
[3]Patricia E G, Amelia C R. A model for determination of multiocomponent diffussion coefficients in food[J]. J Food Engng, 2003, 56: 401-410.
[4]Biuchet R, Meverl R. A numerical inverse method for calculation the interdiffudsion coefficients along a diffusion path in ternary systems[J]. Acta Materials, 2002, 50: 4887-4900.
[5]Oleg O M, Alexander A S. Verifying reciprocal relations for ecperimental diffusion coefficients in multicomponent mixtures[J]. Fluid Phase Equilibria, 2003, 208: 291-301.
[6]MO Ding-cheng. Kinetics of Metallurgy [M]. Changsha: Central South University Press, 1987. 30-52. (in Chinese)
[7]XIN Feng, YIN Xiao-hong, WANG Fu-min, et al. Effective diffusivities of gas diffusion in porous alumina [J]. Journal of Chemical Industry and Engineering, 2001, 52(4): 306-310. (in Chinese)
[8]Muchi I, Yagi J, Tamura K, et al. Reaction kinetics in the blast furnace[J]. Journal of the Japan Institute of Metals, 1966, 30: 826-831.
[9]Patisson F, Francois M G, Ablitzer D. A non-isothermal, non-equimolar transient kinetic model for gas-solid reactions[J]. Chemical Engineering Science, 1998, 53(4): 697-708.
[10]Eddings E G, Sohn H Y. Simplified treatment of the rates of gas-solid reactions involving multicomponent diffusion[J]. Industry Engineering Chemistry Review, 1993, 32: 42-48.
[11]Hindmarsh A C, Johnson S H. Dynamic simulation of multispecies reaction/diffusion in nonisothermal porous spheres[J]. Chemical Engineering Science, 1991, 46: 1445-1463.
[12]Winkelman J G M, Beenackers A A C M. Simultaneous absorption and desorption with reversible first-order chemical reaction analytical solution and negative enhancement factors[J]. Chemical Engineering Science, 1993, 48(16): 2951-2955.
[13]Boaventura R A, Eodrigues A E. Consectutive reactions in fluidized bed biological reactors: modeling and experimental study of wastewater denitrification[J]. Chemical Engineering Science, 1988, 43(10): 2715-2728.
[14]De Groot S R, Mazur P. Non-equilibrium thermodynamics[M]. Amsterdam: North-Holland Pub, 1962. 235-284.
[15]CHEN Yu-fei, CHEN Jia-yong. Mathematical model for diffusion of electrolyte mixtures in porous particles[J]. Journal of Chemical Industry and Engineering, 1992, 43(2):125-131. (in Chinese)
[16]zisik M N. Heat Conduction[M]. New York: John Wiley & Sons Ins, 1993. 502-563.
[17]Tranter C J. Integral Transforms in Mathematical Physics[M]. New York: John Wiley and Sons, 1962. 387-401.
[18]CHEN Fu-zhang, JIN Fu-lin, HU Jia-gan, et al. Mathematical Analysis[M]. Shanghai: Shanghai Science and Technology Press, 1978. 545-583.
[19]SONG Ying-tao, XU Zeng-he. Study of the effect of convection and diffusion on gas-solid reaction in porous media[J]. J Materials and Metallurgy, 2004, 3(3): 176-180.
[20]SONG Ying-tao, XU Zeng-he. Study on gas-solid reaction and convection, reaction and diffusion of gas[J]. J Chinese Rare Earth Society, 2004, 22(Special Issue): 239-244.
(Edited by LONG Huai-zhong)
Foundation item: Project (50136020) supported by the National Natural Science Foundation of China; Project (01056) supported by the Key Project of Education Ministry of China
Received date: 2004-07-09; Accepted date: 2004-11-15
Correspondence: XU Zeng-he, Professor; Tel: +86-24-83681145; E-mail: xuzhenghe@yahoo.com.cn