Risk assessment of water inrush in tunnels based on attribute interval recognition theory
来源期刊:中南大学学报(英文版)2020年第2期
论文作者:李利平 王升 成帅 胡慧江 张明光 文桃
文章页码:517 - 530
Key words:water inrush; risk assessment; attribute interval recognition model; TFN-AHP
Abstract: Water inrush is one of the most serious geological hazards in underground engineering construction. In order to effectively prevent and control the occurrence of water inrush, a new attribute interval recognition theory and method is proposed to systematically evaluate the risk of water inrush in karst tunnels. Its innovation mainly includes that the value of evaluation index is an interval rather than a certain value; the single-index attribute evaluation model is improved non-linearly based on the idea of normal distribution; the synthetic attribute interval analysis method based on improved intuitionistic fuzzy theory is proposed. The TFN-AHP method is proposed to analyze the weight of evaluation index. By analyzing geological factors and engineering factors in tunnel zone, a multi-grade hierarchical index system for tunnel water inrush risk assessment is established. The proposed method is applied to ventilation incline of Xiakou tunnel, and its rationality and practicability is verified by comparison with field situation and evaluation results of other methods. In addition, the results evaluated by this method, which considers that water inrush is a complex non-linear system and the geological conditions have spatial variability, are more accurate and reliable. And it has good applicability in solving the problem of certain and uncertain problem.
Cite this article as: WANG Sheng, LI Li-ping, CHENG Shuai, HU Hui-jiang, ZHANG Ming-guang, WEN Tao. Risk assessment of water inrush in tunnels based on attribute interval recognition theory [J]. Journal of Central South University, 2020, 27(2): 517-530. DOI: https://doi.org/10.1007/s11771-020-4313-2.

J. Cent. South Univ. (2020) 27: 517-530
DOI: https://doi.org/10.1007/s11771-020-4313-2
WANG Sheng(王升)1, 2, LI Li-ping(李利平)1, CHENG Shuai(成帅)1,
HU Hui-jiang(胡慧江)1, ZHANG Ming-guang(张明光)3, WEN Tao(文桃)2
1. Geotechnical and Structural Engineering Research Center, Shandong University, Ji’nan 250061, China;
2. School of Civil Engineering, Yangtze Normal University, Chongqing 408100, China;
3. College of Safety and Environmental Engineering, Shandong University of Science and Technology,Qingdao 266590, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Water inrush is one of the most serious geological hazards in underground engineering construction. In order to effectively prevent and control the occurrence of water inrush, a new attribute interval recognition theory and method is proposed to systematically evaluate the risk of water inrush in karst tunnels. Its innovation mainly includes that the value of evaluation index is an interval rather than a certain value; the single-index attribute evaluation model is improved non-linearly based on the idea of normal distribution; the synthetic attribute interval analysis method based on improved intuitionistic fuzzy theory is proposed. The TFN-AHP method is proposed to analyze the weight of evaluation index. By analyzing geological factors and engineering factors in tunnel zone, a multi-grade hierarchical index system for tunnel water inrush risk assessment is established. The proposed method is applied to ventilation incline of Xiakou tunnel, and its rationality and practicability is verified by comparison with field situation and evaluation results of other methods. In addition, the results evaluated by this method, which considers that water inrush is a complex non-linear system and the geological conditions have spatial variability, are more accurate and reliable. And it has good applicability in solving the problem of certain and uncertain problem.
Key words: water inrush; risk assessment; attribute interval recognition model; TFN-AHP
Cite this article as: WANG Sheng, LI Li-ping, CHENG Shuai, HU Hui-jiang, ZHANG Ming-guang, WEN Tao. Risk assessment of water inrush in tunnels based on attribute interval recognition theory [J]. Journal of Central South University, 2020, 27(2): 517-530. DOI: https://doi.org/10.1007/s11771-020-4313-2.
1 Introduction
With the implementation of “One Belt and Road” initiative, the construction focus in China such as highway, railway, hydraulic and hydroelectric engineering and other major projects is transferred to western karst mountainous areas with complex terrain and geological conditions [1-3]. A number of tunnel projects have emerged, and most of them show obvious characteristics of large buried depth, high stress and strong karst. Because the disaster-causing mechanism is unclear, and the geological conditions along the tunnel can’t be accurately detected, it is difficult to contain water inrush. Once water inrush occurs, it will not only lead to the machine damage and other economic loss, but also cause heavy casualties, and even be forced to change line [4-7]. In order to realize active prevention and control of water inrush, it is very important to study risk assessment theory and methods.
A number of researches on water inrush mechanism were performed based on theoretical analysis, numerical simulation and geo-mechanical model test. LI et al [8] studied the mechanism of water-rock interaction by using karst geology, engineering hydraulics and fracture mechanics, and revealed the mechanism of water inrush process. YANG et al [9] presented a fully coupled flow- stress-damage model based on porous media flow and damage mechanics, and simulated the evolution of water inrush channels. ZHAO et al [10] proposed a seepage-stress coupling method based on 3D digital models, and explored the change law of seepage field, stress field and displacement in the process of water inrush. LI et al [11] and YANG et al [12] carried out a large-scale true triaxial geo-mechanical model test to study the evolution law of multivariate physical information, and then analyzed the mechanism of water inrush.
However, many scholars have conducted quite a few researchers regarding risk management and risk assessment of underground engineering, which is an effective method to predict the occurrence of water inrush. The International Tunnelling Association promulgated “Guidelines for Tunneling Risk Management” to manage and avoid risks in tunnel construction [13]. BUKOWSKI [14] developed a risk assessment system of water flowing considering inflow intensity, suspended material, shaft condition and the mine history. ZHANG et al [15] proposed a quantitative evaluation method of water inrush and a four-color mechanism of disaster warning for high-risk karst tunnels. XU et al [16] analyzed the key influencing factors of water or mud inrush and calculated their weight based on AHP, and then put forward a three- stage risk assessment method in karst tunnels. LI et al [4, 17] established two-stage attribute synthetic evaluation system, which is applied in design stage and construction stage; and then put forward an attribute interval evaluation methodology. In addition, a lot of evaluation models were established to evaluate the water inrush risk in tunnels, such as attribute model [3, 4, 6, 18], cloud model [19], fuzzy model [20, 21], unascertained measure model [5], grey theory [22]. With the development of computer technology, LI et al [23] studied the risk assessment system based on GIS to predict dynamically the water inrush risk in the karst tunnel. LI et al [24, 25] developed risk evaluation software for water inrush, which improved the efficiency of risk management in tunnel construction. But the variability of factors measure values, nonlinearity of evaluation models and the uncertainty of factor weights are not comprehensively considered.
The paper aims to propose a new method to predict the water inrush risk in karst tunnels. The multi-grade hierarchical index system for tunnel water inrush risk assessment is established, and an interval rather than a certain value is used to quantify the evaluation indices. The traditional attribute evaluation model is improved nonlinearly by introducing the idea of normal distribution, and improved intuitionistic fuzzy sets theory is adopted to calculate attribute measure interval. Meanwhile, the weights of multi-grade indices are determined by TFN-AHP. The theory and method realizes the quantitative identification of disaster risk level and provides an effective approach for risk assessment of water inrush in karst tunnels.
2 Improved attribute interval recognition theory
Let X be evaluation object space, and X={x1, …, xi, …, xn}. The object xi has m evaluation indexes Ij (j=1, 2, …, m). Each evaluation index Ij has K risk grades Ck (k=1, 2, …, K). In the work, the attribute space C is defined as risk level of water inrush in karst tunnels, and C={C1, C2, C3, C4}={very high risk, high risk, medium risk, low risk}.
2.1 Single-index attribute measure analysis
According to the measured value tj of evaluation index Ij, the single-index attribute measure function is used to compute the single- index attribute measure μijk which can determine tj belonging to risk level Ck. In general, the single- index attribute measure function is determined according to grade form and grading standard presented in Table 1.
Table 1 Grade subdivision of single index
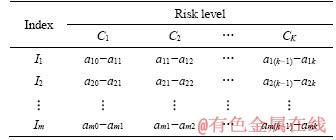
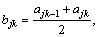 k=1, 2, …, K (1)
k=1, 2, …, K (1)
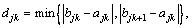 k=1, 2, …, K-1 (2)
k=1, 2, …, K-1 (2)
The common single-index attribute measure function is shown in Figure 1. It can be seen from Figure 1 that the traditional single-index attribute measure function is linear; that is, the attribute measure value exhibits linear change along with measured value of influencing factor. A large number of project experiences show that water inrush in tunnels is a non-linear complex system affected by many factors. Therefore, the non-linear improvement is conducted (Figure 2).
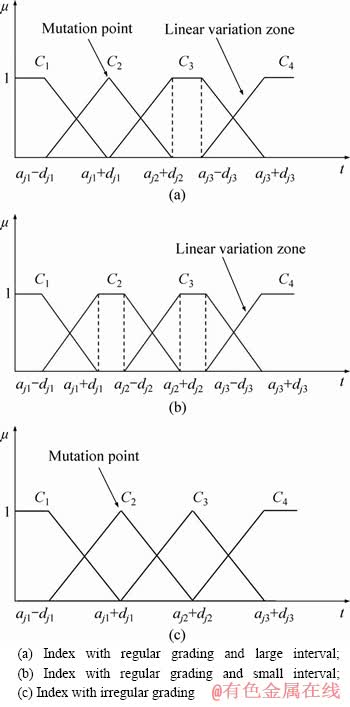
Figure 1 Linear attribute measurement functions:
Figure 2 Non-linear attribute measurement function
The formula of normal distribution (μ, σ2) is as follows:
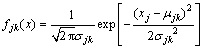 (3)
(3)
where fjk(x) is single-index attribute measure value of the j-th evaluation index belonging to risk level Ck; μjk is the mutation point value of the j-th evaluation index belonging to risk level Ck; σjk is equilibrium coefficient of the j-th evaluation index belonging to risk level Ck. And fjk meets:
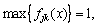 that is
that is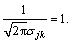
Formula is transformed as follows:
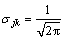 .
.
Formula (3) is simplified by substituting Eq. (4):
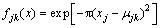 (4)
(4)
From the above equation, when x=-∞ or +∞, fij(x)→0; and fij(xa)=exp[-π]=0.043, approaching to zero. Therefore, let (xj-ujk)∈[0, 1] while let fij(x)∈[0, 1].
When 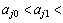 …
…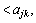
 (5)
(5)
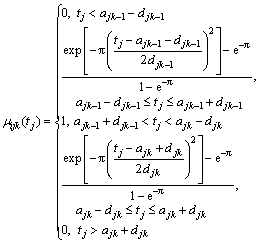 (6)
(6)
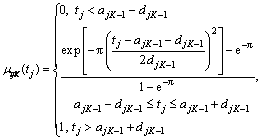 (7)
(7)
When aj0> aj1>…>ajK
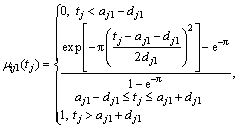 (8)
(8)
 (9)
(9)
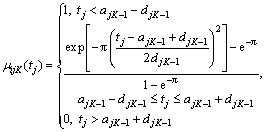 (10)
(10)
where j=1, 2, …, m; k=1, 2, …, K.
2.2 Attribute interval recognition based on intuitionistic fuzzy sets
1) Basic concept of intuitionistic fuzzy sets
Definition 1: concept. For a given universe X, let a intuitionistic fuzzy set A={
Definition 2: score function. The score function not only reflects the size of intuitionistic fuzzy number well, but also accurately expresses support degree for decision-making. Therefore, whether score function is reasonable or not is particularly important. Let α=(uα, vα) be intuitionistic fuzzy value, where (uα, vα) is intuitionistic fuzzy number. Formula (11) is the traditional score function [28, 29], but the value S is often equal, for example (0.6, 0.1) and (0.7, 0.2). Therefore, the score function is improved in Formula (12).
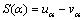 (11)
(11)
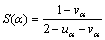 (12)
(12)
2) Attribute interval recognition
The discontinuity and heterogeneity of rock mass medium in the underground space complicate the geological conditions. The more complicated the geological conditions that underground engineering passes through are, the more easily the geological disasters are induced. Therefore, for accurately quantifying the geological parameters, the measured value of evaluation index Ij is quantified in the form of interval [tjx, tjy] considering the complexity and variability of geological conditions. Then the single-index attribute measure matrices of tjx and tjy are respectively calculated by formulae (5)-(10), as follows:
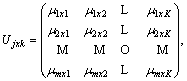
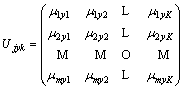 .
.
Let membership degree ujk=min{μjxk, μjyk}, hesitancy degree πjk=max{μjxk, μjyk}-min{μjxk, μjyk}, non-membership degree vjk=1-max{μjxk, μjyk} in the intuitionistic fuzzy set. The intuitionistic fuzzy decision matrix D=(djk)m×K is constructed.
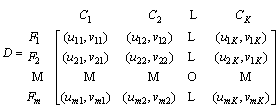 (13)
(13)
The score matrix S=(sjk)m×K is obtained based on score function (12).
2.3 Attribute recognition analysis
After m single-index attribute measure values of evaluation object xi are obtained, the comprehensive attribute measure values μik belonging to every risk grade are calculated as follows:
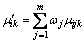 (14)
(14)
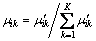 (15)
(15)
where ωj is the weight of the jth index, s.t., 0≤ωj≤1 and 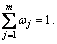
In the attribute recognition model, attribute space F={C1, C2, C3, C4} is an ordered segmentation comment set. On the basis of comprehensive attribute measure matrix, confidence criterion is adopted to identify which risk grade Ck is preferred by the evaluation object xi. The confidence criterion: let an ordered comment set F={C1, C2, …, CK}, the confidence λ∈(0.5, 1], usually between 0.6-0.7.
When C1< C2<…
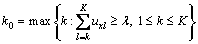 (16)
(16)
x belongs to Ck0.
When C1> C2>…>CK, if
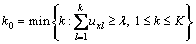 (17)
(17)
x belongs to Ck0.
3 Risk evaluation method of water inrush in tunnels
3.1 Attribute recognition analysis
For a complex dynamic disaster, water inrush in tunnels is caused by the instability of groundwater storage system or groundwater movement system disturbed by outside forces. The occurrence mechanism for a water inrush disaster is very complex and influenced by multiple factors. If selecting too many factors as evaluation indices will weaken the contribution degree of key control factors, thus the accuracy of evaluation results is affected. If fewer factors are selected as evaluation indices, the applicability is limited. In order to resolve the above problem, the multi-grade hierarchical index system for water inrush in tunnels is established. By systematically summarizing and analyzing over 100 cases of water inrush in Chinese tunnels[4, 17, 30], the index system consists of 5 first-grade evaluation indices, which are geology and tectonic I1, ground water I2, topography and geomorphology I3, construction situation I4, climate condition I5. The first-grade indices are divided into 15 second-grade evaluation indices, as shown in Figure 3.
3.2 Grading standards of water inrush risk in tunnels
According to existing management achievement and literature material of water inrush risk in tunnels [3-5, 17, 31], combining with rich field construction experience, each evaluation index is divided into 4 risk levels. The evaluation space is {C1, C2, C3, C4}, i.e., C1={very high risk}, C2={high risk}, C3={medium risk}, C4={low risk}, as shown in Table 2.
Since the evaluation indices such as unfavorable geology I13, crack growth degree I15, rich aquifer I23, surface karst I32, forecast and monitoring technology I41, construction and management level I42 and rainfall season distribution I53, which are mainly of qualitative analysis, are difficultly quantified, the expert evaluation method is used for quantitative grading. The surrounding rock grade is discontinuous and cannot meet the continuous form of data in Table 1. The method of the rock grade is proposed as shown in Table 2. And the values are only taken as integers. The formation lithology can be graded by expert evaluation method or rock layer solubility [4, 6, 17]. According to Ref. [30], the single-index attribute measure of attitude of rocks is represented by 0 or 1. The other evaluation indices can use formulae (5)- (10) to construct single-index attribute measure function.
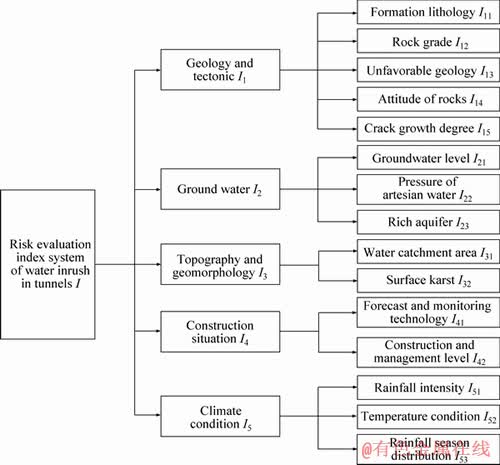
Figure 3 Risk evaluation index system of water inrush in tunnels
3.3 Weight method based on TFN-AHP
The weight reflects the importance of each evaluation index to evaluation object. Whether the weight is accurate or not directly affects the evaluation results. At present, the common weight methods can be divided into subjective weighting method and objective weighting method. The subjective weighting method is to calculate the weight by constructing judgement matrix, which is obtained by comparing the importance of each risk factor in pairs, such as AHP [6, 32, 33], expert grade method. This method can give full play to experts’ experience, but it is easy to be influenced by decision maker’s experience, thinking mode and individual preference. Therefore, the weight is subjectively random. The objective weighting method is to calculate the weight by the difference of evaluation index data, such as entropy method and variation coefficient method. This method avoids the bias caused by human factors, but has high requirements for the evaluation index data, and the importance degree of evaluation index in the actual situation is neglected. In order to overcome the shortcoming of the above methods, the triangular fuzzy number theory is used to optimize the judgment matrix [34]. Meanwhile, possibility degree matrix is introduced to solve consistency check of judgment matrix and calculation difficulty of factor weight in the traditional AHP.
3.3.1 Preparative knowledge of triangular fuzzy number theory
Let fuzzy number M=(l, m, u), s.t., l≤m≤u and l>0. The l, m and u are minimum possible value,middle value and maximum possible value of M respectively, which called a triangular fuzzy number of M. The operational rule is determined by arbitrarily selecting two triangular fuzzy numbers M1=(l1, m1, u1) and M2=(l2, m2, u2).
1) 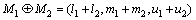 ;
;
2) 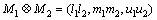 ;
;
3) 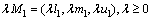 ;
;
4) 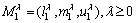 ;
;
5) 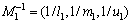 .
.
Table 2 Indices and criteria for risk assessment of water inrush
3.3.2 Weight method
Step 1: According to 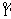 -
-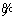 triangular fuzzy scale method (Table 3), the judgment matrix M=(dij)n×n is constructed by experts.
triangular fuzzy scale method (Table 3), the judgment matrix M=(dij)n×n is constructed by experts.
dji=(dij)-1 (18)
where dij is importance degree of Ii relative to Ij,and is also a triangular fuzzy number.
Table 3 Scale method of triangular fuzzy linguistic variables
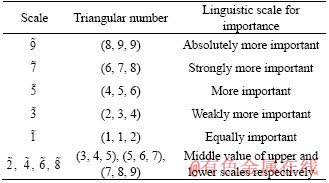
Step 2: The comprehensive fuzzy number of evaluation index Ii is calculated. Then the comprehensive triangular fuzzy number Mi is determined.
 (19)
(19)
where i and j=1, 2, …, n.
Step 3: The defuzzification of comprehensive triangular fuzzy number Mi is conducted. Let Mi=(li, mi, ui) and Mj=(lj, mj, uj), possibility degree of Mi≥Mj is
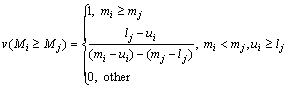 (20)
(20)
Step 4: Let ωi′=minv(Mi≥M1, M2, …, Mi-1, Mi+1, …, Mn), i=1, 2, …, n. The W′=(ω1′, ω2′, …, ωn′) is obtained. Then W′ is made normalized processing. Finally, weight vector of evaluation index is determined as follows:
W=(ω1, ω2, …, ωn)T (21)
3.4 Water inrush risk assessment procedure in tunnels
The risk evaluation procedure of water inrush in tunnels based on improved attribute interval recognition model is as follows:
1) A multi-grade hierarchical index system for water inrush in tunnels is established. Index set I={ I1, I2, I3, I4, I5} can be divided into 5 index subsets according to some attribute. For example, I1={ I11, I12, I13, I14, I15}.
2) The judgment matrix M is constructed based on 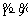 triangular fuzzy scale method. The weight vector W of first-grade evaluation indices and the weight vector Wj (j=1, 2, …, 5) of second-grade evaluation indices are calculated according to formulae (18)-(20).
triangular fuzzy scale method. The weight vector W of first-grade evaluation indices and the weight vector Wj (j=1, 2, …, 5) of second-grade evaluation indices are calculated according to formulae (18)-(20).
3) The measured interval value [tjrx, tjry] of second-grade evaluation indices belonging to Ij (j=1, 2, …, 5) is determined by experienced experts based on detailed data of geological survey and construction information. The single-index attribute measures of tjrx and tjry are respectively calculated by formulae (5)-(10). The single-index attribute measure matrices Ujx and Ujy of Ij are formed.
4) The intuitionistic fuzzy decision matrix is constructed. The score matrix is obtained according to formula (12). The comprehensive attribute measure vector is calculated according to formulae (14)-(15). Finally, the risk grade of water inrush in tunnels is determined according to formulae (16)-(17).
4 Engineering applications
4.1 Engineering background of Xiakou tunnel
The Xiakou tunnel is a dominant engineering of the expressway from Yichang to Badong, located in Xiakou Town, Xingshan County, Hubei Province. It passes through a south-north mountain and has two separate lanes, with the left line length 6456.0 m and right line length 6487.0 m. The Xiakou tunnel is a deep and extra-long with a maximum burial depth of 1500 m. The geomorphic unit of tunnel area belongs to low semi mountainous gorge area with layered monoclinic of structural denudation and corrosion. The mountain strata is composed of the carbonate rock intercalated with clastic rock from Cambrian to Triassic period, in which the carbonate rock is soluble rock. The surface karst forms such as karst marsh land, funnels and falling water holes are well developed in combination. The geological conditions and the karst hydrologic conditions are extremely complex, especially in the section from K107+800 to K109+700 of Xiakou tunnel. The engineering geological profile of tunnel section K107+800-K109+700 is shown in Figure 4.
There is a ventilation incline on the left line of Xiakou tunnel. The dip of ventilation incline is 24.5° and its overall length is 780.95 m. The spatial relationship of ventilation incline and Xiakou tunnel is presented in Figure 5. In Figure 5, “K108+…” represents the distance numbers of Xiakou tunnel, while “XJK0+…” represents the distance numbers of ventilation incline. In this paper, the water inrush risk for XJK0+110- XJK0+060 section of ventilation incline is evaluated by attribute interval recognition theory proposed.
4.2 Risk assessment of water inrush
4.2.1 Determination of weights with TFN-AHP
The experienced tunnel expert is invited to construct fuzzy judgment matrixes of evaluation indices by  triangular fuzzy scale method. Then, the weight vectors are determined according to Eqs. (18)-(20).
triangular fuzzy scale method. Then, the weight vectors are determined according to Eqs. (18)-(20).
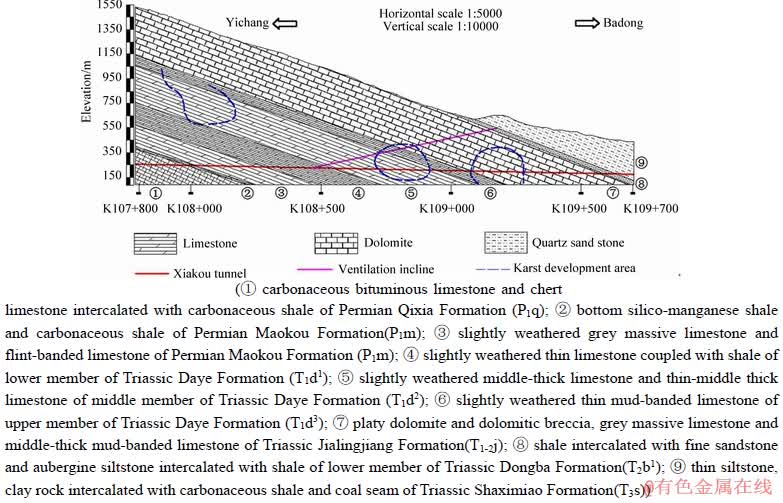
Figure 4 Engineering geological profile of Xiakou tunnel [17, 19]
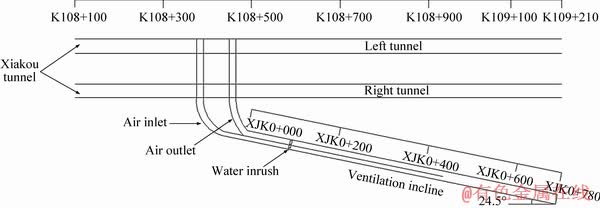
Figure 5 Spatial relationship of ventilation incline and Xiakou tunnel [17, 19]
Table 4 Fuzzy judgment matrix of evaluation index I1
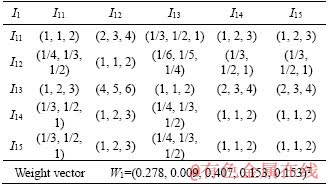
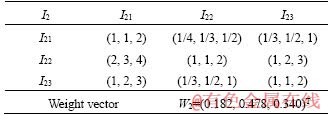
Table 5 Fuzzy judgment matrix of evaluation index I2
4.2.2 Risk assessment analysis of water inrush
By comprehensive analysis of geological investigation data, geological sketch and advanced geological prediction, the indices value of geology and tectonic I1 and ground water I2 are determined. According to geological survey combining with locale exploration, topography and geomorphology I3 is quantified. The values of construction situation I4 are obtained based on the construction and management level of the unit and the implementation situation of monitoring and forecast. The values of climate condition I5 are obtained based on meteorological and climatic data from the location of the tunnel.
Table 6 Fuzzy judgement matrix of evaluation index I5

Table 7 Fuzzy judgement matrix of first-grade evaluation index I
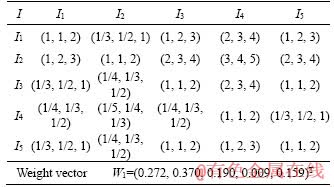
According to single-index attribute measure function in this paper, the attribute measure value of measured interval value [tjx, tjy] for evaluation indices is calculated. Based on intuitionistic fuzzy sets theory, single-index attribute measure intervals are determined, as shown in Table 8.
The improved score function (10) in this paper is used to calculate the single-index attribute measure intervals of second-grade evaluation indices, and then the support degrees that can accurately describe the single index belonging to each risk level are obtained, as shown in Table 9.
According to formula (12), the comprehensive attribute measure values of second-grade indices and first-grade indices are calculated respectively. It is worth mentioning that the comprehensive attribute measure values of second-grade indices are taken as single-index attribute measure values of first-grade indices. The initial comprehensive attribute measure values are normalized by formula (16), and the final comprehensive attribute measure value can be obtained, as shown in Table 10.
The higher the risk of water inrush, the lower the probability of occurrence. So, let the ordered set (C1, C2, C3, C4) meet C1
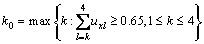 .
.
If k=2, 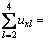 0.342+0.278+0.014=0.634< 0.65, the inequality doesn’t hold.
0.342+0.278+0.014=0.634< 0.65, the inequality doesn’t hold.
Table 8 Single-index attribute measure intervals
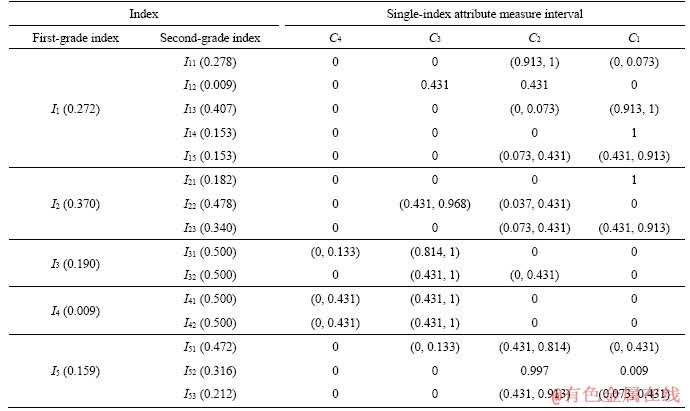
Table 9 Single-index attribute measure of second-grade indices
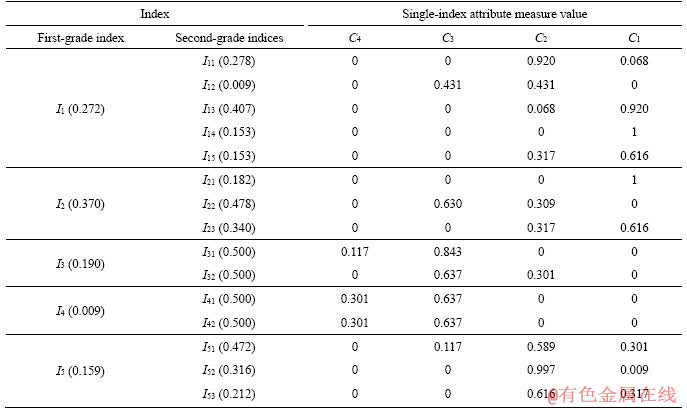
Table 10 Attribute measure calculation of multi-grade evaluation indices
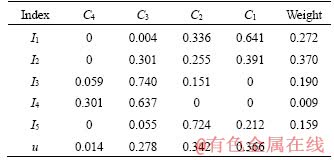
If and only if k=1,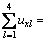 0.366+0.342+0.278+0.014=1>0.65, the inequality holds. Therefore, the risk level of water inrush in the section XJK0+110-XJK0+060 is C1. That is very high risk. According to the previous studies, the risk level was evaluated as C1 (very high risk) based on the attribute mathematical theory [17] and the novel cloud model [19]. The evaluation result in this paper shows good agreement with the former results. Furthermore, the prediction result obtained by using attribute interval recognition theory in this paper coincides with the actual condition. On August 7, 2011, water inrush occurred from blast holes in the left side of ventilation incline face XJK0+101; the jet distance was approximately 4 m; and the inflow of water was 64 m3/h, as shown in Figure 6(a). Until August 30, 2011, the total inflow of water was about 28000 m3, as shown in Figure 6(b). The attribute interval recognition theory is verified to be useful for the risk assessment of water inrush. Moreover, the method can provide better accuracy and satisfy the requirement for practical projects.
0.366+0.342+0.278+0.014=1>0.65, the inequality holds. Therefore, the risk level of water inrush in the section XJK0+110-XJK0+060 is C1. That is very high risk. According to the previous studies, the risk level was evaluated as C1 (very high risk) based on the attribute mathematical theory [17] and the novel cloud model [19]. The evaluation result in this paper shows good agreement with the former results. Furthermore, the prediction result obtained by using attribute interval recognition theory in this paper coincides with the actual condition. On August 7, 2011, water inrush occurred from blast holes in the left side of ventilation incline face XJK0+101; the jet distance was approximately 4 m; and the inflow of water was 64 m3/h, as shown in Figure 6(a). Until August 30, 2011, the total inflow of water was about 28000 m3, as shown in Figure 6(b). The attribute interval recognition theory is verified to be useful for the risk assessment of water inrush. Moreover, the method can provide better accuracy and satisfy the requirement for practical projects.
5 Conclusions
1) A new attribute interval recognition theory and method is proposed based on improved attribute evaluation model and intuitionistic fuzzy sets theory. The measure value of evaluation index is an interval rather than a certain value. The index weights are determined by improved TFN-AHP. The methodology solves the variability of geological condition, nonlinearity of evaluation model and the uncertainty of weight.

Figure 6 Verification by excavation result [17, 19]:
2) Based on the information of water inrush examples in karst tunnels, geology and tectonic I1, ground water I2, topography and geomorphology I3, construction situation I4, climate condition I5 are selected as risk evaluation indices. Five first-grade evaluation indices are divided into 15 second-grade evaluation indices. Therefore, a multi-grade hierarchical index system for tunnel water inrush risk assessment is established, which fully considers the influencing factors, and does not affect the accuracy of evaluation results.
3) This new theory and method in the paper is successfully applied to ventilation incline XJK0+110-XJK0+060 section of Xiakou tunnel. The evaluation result is not only consistent with the results of attribute mathematical theory and the novel cloud model, but only shows good agreement with the actual situation, which provides a new way for water inrush risk evaluation method in karst tunnels.
References
[1] LI T Z, YANG X L. Risk assessment model for water and mud inrush in deep and long tunnels based on normal grey cloud clustering method[J]. KSCE Journal of Civil Engineering 2018, 22(5): 1991-2001. DOI 10.1007/s12205-017-0553-6
[2] LI X Z, HUANG Z, XU Z H. Hazard-causing structures for water and mud inrush in tunnels and the corresponding detailed, multiscale observation technology [J]. China Journal of Highway and Transport, 2018, 31(10): 79-90. (in Chinese)
[3] WANG J, LI S C, LI L P, LIN P, XU Z H, GAO C L. Attribute recognition model for risk assessment of water inrush [J]. Bulletin of Engineering Geology and the Environment, 2017, 78(2): 1057-1071. DOI 10.1007/s10064-017-1159-4.
[4] LI S C, ZHOU Z Q, LI L P, XU Z H, ZHANG Q Q, SHI S S. Risk assessment of water inrush in karst tunnels based on attribute synthetic evaluation system [J]. Tunnel Underground Space Technology, 2013, 38: 50-58. DOI: https://doi.org/10.1016/j.tust.2013.05.001.
[5] LI S C, WU J, XU Z H, LI L P. Unascertained measure model of water and mud inrush risk evaluation in karst tunnels and its engineering application [J]. KSCE Journal of Civil Engineering, 2017, 21(4): 1170-1182. DOI 10.1007/s12205- 016-1569-z.
[6] WANG S. Regional dynamic risk assessment and early warning of tunnel water inrush and application [D]. Ji’nan: Shandong University, 2016. (in Chinese)
[7] ZhANG D, FANG Q, LOU H. Grouting techniques for the unfavorable geological conditions of Xiang’an subsea tunnel in China [J]. Journal Rock Mechanics and Geotechnical Engineering, 2014, 6(5): 438-446. DOI: http://dx.doi.org/ 10.1016/j.jrmge.2014.07.005.
[8] LI Li-ping, LI Shu-cai, ZHANG Qing-song. Study of mechanism of water inrush induced by hydraulic fracturing in karst tunnels [J]. Rock and Soil Mechanics, 2010, 31(2): 523-528. DOI:10.16285/j.rsm.2010.02.016.
[9] YANG T H, LIU J, ZHU W C, ELSWORTH D, THAM L G, TANG C A. A coupled flow-stress-damage model for groundwater outbursts from an underlying aquifer intomining excavations [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44: 87-97. DOI: https://doi.org/10.1016/j.ijrmms.2006.04.012.
[10] ZHAO J, YIN L, GUO W. Stress–seepage coupling of cataclastic rock masses based on digital image technologies [J]. Rock Mechanics and Rock Engineering, 2018, 51: 2355-2372. DOI: https://doi.org/10.1007/s00603-018- 1474-5.
[11] LI S C, GAO C L, ZHOU Z Q, LI L P, WANG M X, YUAN Y C, WANG J. Analysis on the precursor information of water inrush in karst tunnels: A true triaxial model test study [J]. Rock Mechanics and Rock Engineering, 2019, 52: 373-384. DOI: https://doi.org/10.1007/s00603-018-1582-2.
[12] YANG W M, WANG M X, ZHOU Z Q, LI L P, YUAN Y C, GAO C L. A true triaxial geomechanical model test apparatus for studying the precursory information of water inrush from impermeable rock mass failure [J]. Tunnelling and Underground Space Technology, 2019, 93: 103078. DOI: https://doi.org/10.1016/j.tust.2019.103078.
[13] ESKESEN S D, TENGBORG P, KAMPMANN J, VEICHERTS T H. Guidelines for tunnelling risk management: International tunneling association [J]. Tunnelling and Underground Space Technology, 2004, 19(3): 217-237. DOI: 10.1016/j.tust. 2004.01.001.
[14] BUKOWSKI P. Water hazard assessment in active shafts in upper Silesian Coal Basin mines [J]. Mine Water and the Environment, 2011, 30(4): 302-311. DOI: 10.1007/ s10230-011-0148-2.
[15] ZHANG Q S, LI S C, HAN H W, GE Y H, LIU R T, ZHANG X. Study on risk evaluation and water inrush disaster preventing technology during construction of karst tunnels [J]. Journal of Shandong University: Engineering Science, 2009, 39(3): 106-110. (in Chinese)
[16] XU Z H, LI S C, LI L P, HOU J G, SUI B, SHI S S. Risk assessment of water or mud inrush of karst tunnels based on analytic hierarchy process [J]. Rock and Soil Mechanics, 2011, 32(6): 1757-1766. (in Chinese)
[17] LI S C, ZHOU Z Q, LI L P, SHI S S, XU Z H. Risk evaluation theory and method of water inrush in karst tunnels and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1858-1867. (in Chinese)
[18] LI L P, ZHOU Z Q, LI S C, XUE Y G, XU Z H, SHI S S. An attribute synthetic evaluation system for risk assessment of floor water inrush in coal mines [J]. Mine Water and the Environment, 2015, 3(34): 288-294. DOI 10.1007/s10230-014-0318-0.
[19] WANG Y C, YIN X, JING H W, LIU R C, SU H J. A novel cloud model for risk analysis of water inrush in karst tunnels [J]. Environmental Earth Science, 2016, 75: 1450. DOI 10.1007/s12665-016-6260-7.
[20] CHU H D, XU G L, YASUFUKU N., YU Z, LIU P L, WANG J F. Risk assessment of water inrush in karst tunnels based on two-class fuzzy comprehensive evaluation method [J]. Arabian Journal of Geosciences, 2017, 10: 179. DOI: 10.1007/s12517-017- 2957-5.
[21] YUAN Y C, LI S C, ZHANG Q Q, LI L P, SHI S S, ZHOU Z Q. Risk assessment of water inrush in karst tunnels based on a modified grey evaluation model: Sample as Shangjiawan Tunnel [J]. Geomechanics and Engineering, 2016, 11(4): 493-513. DOI: https://doi.org/10.12989/ gae.2016.11.4.493.
[22] ZHANG K, TANNANT D D, ZHENG W B, CHEN S G, TAN X R. Prediction of karst for tunnelling using fuzzy assessment combined with geological investigations [J]. Tunnelling and Underground Space Technology, 2018, 80: 64-77. DOI: https://doi.org/10.1016/j.tust.2018.06.009.
[23] LI Xue-ping, LI Yun-an. Research on risk assessment system for water inrush in the karst tunnel construction based on GIS: Case study on the diversion tunnel groups of the Jinping II Hydropower Station [J]. Tunnelling and Underground Space Technology, 2014, 40: 182-191. DOI: http://dx.doi.org/10.1016/j.tust.2013.10.005.
[24] LI L P, LEI T, LI S C, ZHANG Q Q, XU Z H, SHI S S, ZHOU Z Q. Risk assessment of water inrush in karst tunnels and software development [J]. Arabian Journal of Geosciences, 2015, 8: 1843-1854. DOI: 10.1007/s12517-014-1365-3
[25] LI L P, LEI T, LI S C, XU Z H, XUE Y G, SHI S S. Dynamic risk assessment of water inrush in tunnelling and software development [J]. Geomechanics and Engineering, 2015, 9(1): 57-81. DOI: https://doi.org/10.12989/gae.2015.9.1.057
[26] ATANASSOV K T. Intuitionistic fuzzy sets [J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96. DOI: https://doi.org/ 10.1016/S0165-0114(86)80034-3.
[27] ATANASSOV K T. Intuitionistic fuzzy sets: Theory and application [M]. Heidelberg: Physica-Verlag, 1999.
[28] XU Z S, YAGER R R. Some geometric aggregation operators based on intuitionistic fuzzy sets [J]. International Journal of General System, 2006, 35(4): 417-433. DOI: https://doi.org/10.1080/03081070600574353.
[29] KUMAR K, GARG H. Connection number of set pair analysis based TOPSIS method on intuitionistic fuzzy sets and their application to decision making [J]. Applied Intelligence, 2018, 48(8): 2112-2119. DOI: https://doi.org/ 10.1007/s10489-017-1067-0.
[30] YIN Y, TIAN J, ZHANG Y J. Study on statistical analysis of karst tunnel disaster cases [J]. Highway Engineering, 2018, 43(4): 210-214. (in Chinese)
[31] ZHOU Z Q, LI S C, LI L P, SHI S S, WANG K. Attribute recognition model of fatalness assessment of water inrush in karst tunnels and its application [J]. Rock and Soil Mechanics, 2013, 34(3): 818-826. (in Chinses)
[32] WANG S, WEN T, YING S, CAI F, PANG B. Engineering application of attribute model with varying weights in risk identification of high and steep slope in Three Gorges Reservoir Area [J]. Ecology and Environmental Monitoring of Three Gorges, 2017, 2(4): 59-65.
[33] ZHANG K, ZHENG W B, XU C, CHEN S G. Risk assessment of gas outburst in tunnels in non-coal formation based on the attribute mathematical theory [J]. Geomatics, Natural Hazards and Risk, 2019, 10(1): 483-504. DOI: https://doi.org/10.1080/19475705.2018.1530305.
[34] ZHANG K, ZHENG W B, XU C, CHEN S G. An improved extension system for assessing risk of water inrush in tunnels in carbonate karst terrain [J]. KSCE Journal of Civil Engineering, 2019. DOI 10.1007/s12205-019-0756-0.
(Edited by YANG Hua)
中文导读
基于改进属性区间辨识模型的隧道突涌水灾害风险评价方法
摘要:突涌水灾害是地下工程建设过程中最严重的地质灾害之一。为了实现突涌水灾害的有效主动防控,提出了一种新的属性区间辨识模型来系统地评价岩溶隧道突涌水风险。其创新主要在于评价指标的取值是一个区间,而不是一个确定值;引入正态分布理念对传统属性综合评价模型进行非线性改进,提出基于改进直觉模糊理论的综合属性区间测度分析方法;并采用TFN-AHP法进行突涌水评价指标权重分析。同时,通过分析岩溶隧道突涌水灾害的地质影响因素和工程影响因素,建立了一个多层次突涌水风险评价指标体系。将建立的评价方法应用于峡口隧道斜井某段的突涌水风险分析,通过与现场情况和其他方法的评估结果对比,验证了该方法的合理性与实用性。此外,本方法考虑了突涌水这一复杂非线性系统与围岩的空间变异性,评价结果更准确、可靠;且在解决确定与不确定问题方面具有较好的适用性。
关键词:突涌水灾害;风险评价;属性区间辨识模型;三角模糊层次分析法
Foundation item: Project(51722904) supported by the National Science Fund for Excellent Young Scholars, China; Project(51679131) supported by the National Natural Science Foundation of China; Project(2019JZZY010601) supported by the Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project), China; Project(KJ1712304) supported by the Science and Technology Research Program of Chongqing Municipal Education Commission, China; Project(2016XJQN13) supported by the Yangtze Normal University Research Project, China
Received date: 2019-06-08; Accepted date: 2019-12-09
Corresponding author: LI Li-ping, PhD, Professor; Tel: +86-13853182832; E-mail: liliping@sdu.edu.cn; ORCID: 0000-0003-0947- 757X

