J. Cent. South Univ. (2020) 27: 2173-2184

DOI: https://doi.org/10.1007/s11771-020-4439-2

Numerical simulation of intelligent compaction for subgrade construction

MA Yuan(马源)¹, LUAN Ying-cheng(栾英成)¹, ZHANG Wei-guang(张伟光)¹, ZHANG Yu-qing(张裕卿)^{2, 3}

1. School of Transportation, Southeast University, Nanjing 210096, China;

2. National Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology, Changsha 410114, China;

3. Aston Institute of Materials Research, Engineering Systems & Management Group, Aston University,Birmingham, B4 7ET, UK

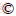Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: During the compaction of a road subgrade, the mechanical parameters of the soil mass change in real time, but current research assumes that these parameters remain unchanged. In order to address this discrepancy, this paper establishes a relationship between the degree of compaction K and strain ε. The relationship between the compaction degree K and the shear strength of soil (cohesion c and frictional angle φ) was clearly established through indoor experiments. The subroutine UMAT in ABAQUS finite element numerical software was developed to realize an accurate calculation of the subgrade soil compaction quality. This value was compared and analyzed against the assumed compaction value of the model, thereby verifying the accuracy of the intelligent compaction calculation results for subgrade soil. On this basis, orthogonal tests of the influential factors (frequency, amplitude, and quality) for the degree of compaction and sensitivity analysis were carried out. Finally, the ‘acceleration intelligent compaction value’, which is based on the acceleration signal, is proposed for a compaction meter value that indicates poor accuracy. The research results can provide guidance and basis for further research into the accurate control of compaction quality for roadbeds and pavements.

Key words: intelligent compaction; numerical simulation; dynamic change; control indicators; orthogonal experiment

Cite this article as: MA Yuan, LUAN Ying-cheng, ZHANG Wei-guang, ZHANG Yu-qing. Numerical simulation of intelligent compaction for subgrade construction [J]. Journal of Central South University, 2020, 27(7): 2173-2184. DOI: https://doi.org/10.1007/s11771-020-4439-2.

1 Introduction

Subgrade compaction quality is critical because it greatly affects the final degree of compaction as well as the subgrade’s modulus and integrity. To overcome disadvantages of traditional compaction processes in which the degree of compaction is dependent mostly on the roller operator’s experience, the concept of intelligent compaction technology has been proposed and has developed rapidly [1-3]. Intelligent compaction technology incorporates a series of new technologies, such as precision sensing technology, computer technology, high-precision positioning technology, electro-hydraulic control technology,and other high-tech technologies, for compaction control. Intelligent compaction technology can realize the integrated control of machine, electricity, liquid, and information about the compacting equipment, and transmit the information to the client in real time. In addition, adaptive and self- learning technologies (such as B-P neural networks) have been introduced to adjust various working　parameters of the body continuously in response to the analysis of relevant information transmitted by high-precision sensors to achieve the highest compaction efficiency and the best compaction quality [4]. Intelligent compaction technology records and displays compaction information that includes the number of roller passes, roller speed, loose laying depth, and roller parameters (amplitude and frequency). Also, several indicators can be used to evaluate the compaction quality of roads, such as acceleration amplitude [5, 6], harmonic value ratio [7], the compaction meter value (CMV) [8-11] compaction control value, and machine drive power [12]. Among these indicators, the CMV is the most widely used to evaluate compaction quality.

Calculation of the CMV is as follows. First, the acceleration signal of the vibration wheel is collected and the Fourier transform is discretized. The second harmonic amplitude in the obtained frequency signal is divided by the first harmonic amplitude and then multiplied by a fixed coefficient to obtain the CMV. The CMV can be used to reflect the stiffness of the compacted material. The higher the CMV value, the greater the stiffness of the compacted material, and vice versa. Compared with traditional compaction quality evaluation indicators, the CMV has the advantage of allowing real-time and comprehensive detection and identifying the uniformity and stability of the compaction.

However, current intelligent compaction technology still has some shortcomings in the following three aspects. First, the intelligent compaction measurement value is based mostly on results obtained from field tests and regression analysis; therefore, this value contains certain inherent errors [13]. Second, for the numerical simulation of intelligent compaction technology, the input parameters, which include parameters for the roller and compacted material, are fixed. Compared with practice, errors are associated with such fixed parameters [14, 15]. For example, as the soil is compacted gradually, the shear strength indices (cohesion c and friction angle φ) of the soil continue to increase, but this change is not taken into account in the numerical simulation. Third, higher harmonics are not taken into account in the calculation of the CMV in the later stages of compaction, which leads to errors in the calculation of the CMV. This shortcoming is a common problem when using the CMV as an evaluation indicator.

This paper establishes a relationship between the degree of compaction K and the strain value ε. The relationship between the degree of compaction K and the mechanical parameters c and φ is derived theoretically. A separate indoor test was performed to develop a UMAT subroutine. In this way, the real-time variations of the soil mechanical parameters during compaction can be identified. The displacement and degree of compaction of the soil compaction process and the dynamic response rules of the CMV also were analyzed in this study. Due to calculation errors associated with the CMV, this paper proposes a more precise compaction quality control indicator, referred to as the acceleration intelligent compaction value (AICV), to provide guidance and a theoretical reference for the intelligent compaction of subgrade soil. In addition, using numerical simulations, orthogonal tests were carried out to assess three roller input factors (frequency, amplitude, and quality) that affect compaction quality, and sensitivity analysis of each factor was carried out. The most significant factors that affect compaction quality were identified and provide reference for adjusting the input parameters for the intelligent compaction of subgrade soil.

2 Methodology

In order to simulate the characteristics of the mechanical parameters as they change in real time during road compaction, the relationship between the degree of compaction K and strain ε was established in this study using a formula derivation. In this way, only the strain values in three directions at any point needed to be collected, and then the degree of compaction at any point could be calculated. In the laboratory tests, cylindrical specimens with degrees of compaction of 80%, 85%, 90%, 93%, 94%, 96% and 100% were prepared for direct shear testing. The cohesion c and friction angle φ of the soil under different degrees of compaction were obtained from the direct shear tests. The relationships between the degree of compaction K and cohesion c and frictional angle φ were obtained by formula fitting, and in this way, the relationships among strain ε, cohesion c, and frictional angle φ of the soil also could be established.

In order to analyze the changes in the degree of compaction during compaction, a model was established and calculated using ABAQUS finite element numerical simulation software. Also, the ABAQUS subroutine UMAT was developed to determine the dynamic changes of the soil parameters. Using a 3×3 orthogonal test table, orthogonal tests of the influential factors (frequency, amplitude, quality) of the roller parameters in terms of compaction quality were carried out. The CMVs for nine cases were calculated via numerical simulation and the subroutine UMAT. Also, the sensitivity of each input parameter of the roller to the degree of compaction was analyzed. The most significant factors that affect compaction quality were determined and some suggestions are given for practical engineering.

As mentioned earlier, the CMV calculation has inherent problems, notably that high harmonics are not considered. When the soil mass reaches a certain compaction state, high-order harmonics appear, resulting in inaccurate CMV calculations. In response, a more accurate evaluation index of compaction quality, the AICV, is herein proposed that can evaluate the compaction quality more objectively and reasonably than the CMV.

2.1 Relationship between degree of compaction K and strain ε

During the subgrade compaction process, the strain of the subgrade soil should correlate well with the degree of compaction [16-18]. At the beginning of the process, the materials are loosely connected and the compaction energy can induce high magnitudes of strain [19]. During compaction, the soil particles gradually become compacted, resulting in less room for the particles to move and rotate, and thus, the strain values decrease accordingly. Establishing a mathematical model (within the linear elastic range) that relates the degree of compaction and strain value would be helpful to provide a direct way to calculate the degree of compaction via strain values. The strain values potentially can be obtained by monitoring the displacement of the soil during compaction. The following assumptions were made in this study during the mathematical model development.

1) Soil particles deform slightly during the compaction process and the strain value is small compared with the size (length, width, and height; x, y and z, respectively) of the original model, and the model is still a cuboid.

2) The initial state of the soil satisfies three basic assumptions of soil mechanics: continuity, uniformity, and isotropy.

First, the initial degree of compaction of the soil was set at 0.8. According to the three basic assumptions, the model volume V₁ can be calculated using Eq. (1) for the compaction process.

V₁=xyz(1+ε₁)(1+ε₂)(1+ε₃)                  (1)

Compaction K is calculated according to Eq. (2):

K=ρ/ρ_max                                                  (2)

Density ρ is calculated according to Eq.(3):

p=m/V                                  (3)

where K is the degree of compaction, ρ is the density that corresponds to the current degree of compaction K, ρ_max is the maximum dry density, m is the quality that corresponds to density ρ, V is the volume that corresponds to density ρ.

During compaction, the quality m does not change, and the maximum dry density ρ_max does not change; only the volume V and density ρ change in real time. As a result, Eq. (4) concludes the process.

K=m/[xyz(1+ε₁)(1+ε₂)(1+ε₃)ρ_max]                     (4)

In addition,

ρ₁=m/(xyz)                              (5)

where ρ₁ is the initial density.

Equations (4) and (5) are combined to obtain Eq. (6):

K=ρ₁/[(1+ε₁)(1+ε₂)(1+ε₃)ρ_max]                        (6)

From assumptions 3, the initial degree of compaction is 0.8, and substituting this value into Eq. (6) gives Eq. (7).

K=0.8/(1+ε₁)(1+ε₂)(1+ε₃)                   (7)

By establishing the relationship between the medium ‘field variable’ degree of compaction K and strain ε, the real-time degree of compaction K is obtained in the finite element simulation. The established formula not only can be used in finite element numerical simulations to obtain the compaction degree of any point, but also can be applied for other aspects. For example, it can be used to calculate the degree of compaction of the soil in field tests or laboratory tests. In the following sections, the relationships between the degree of compaction K and each of the soil strength indicators, c and φ, are established to account for the real-time variation of the soil parameters during the compaction process.

2.2 Relationships between degree of compaction K and cohesion c and phase angle φ

In this study, the soil sample was taken from silty clay in Shandong Province, China, and direct shear tests of soil samples with different degrees of compaction were carried out, as shown in Figure 1. The c and φ values of the soil mass with different degrees of compaction were obtained to provide the mechanical parameters of the soil mass for the next numerical simulation. The relationships between the degree of compaction and c and φ values of the soil mass were defined through data fitting.

Direct shear tests with degrees of compaction of 80%, 85%, 90%, 93%, 94%, 96% and 100% were carried out. The soil mass required by specimens with different degrees of compaction was calculated according to the direct shear test process [20], as described by Eq. (8).

m=ρ_dmaxK(1+ω)V                         (8)

where m is the quality of the soil required for different degrees of compaction (g); ρ_dmax is the maximum dry density of the soil (g/cm³); K is the degree of compaction; ω is the water content (%); V is the hydrostatic bucket volume (cm³).

Figure 1 Direct shear testing in laboratory

In this study, four samples were taken and the tests were repeated by applying 100, 200, 300 and 400 kPa of vertical stress. This can also be seen from the experimental results in Figure 3.

2.3 Establishment of finite element numerical simulation model

2.3.1 Subroutine UMAT

ABAQUS is a powerful finite element software for engineering simulation, whose solutions range from relatively simple linear analysis to many complex nonlinear problems. The finite element software ABAQUS was adopted in this study to evaluate any changes in the degree of compaction during the compaction process as well as to identify the most influential factors [21, 22]. The potential factors considered are c and φ. A subroutine, UMAT, reads the ε₁, ε₂ and ε₃ of the model body in real time [23-26]. With the degree of compaction K as the intermediate variable, dynamic changes in the mechanical parameters of the soil during the compaction process can be determined.

2.3.2 Subgrade structure and mesh

According to previous studies [27-32], the range of influence of the vibration wheel in the horizontal direction during compaction is about 5 m, so the length and width of the numerical model are each 10 m. During actual construction, the thickness of the pavement is 20 cm to 30 cm. In this study, 30 cm was used, and 3.7 m was used for the lower foundation. Tables 1 and 2 present the parameters of the compacted soil.

Table 1 Mechanical parameters of soil

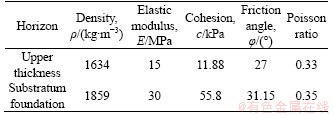
Table 2 Basic parameters of roller

The selection of the mesh density not only should ensure the accuracy of the numerical simulation, but also maintain sufficient computational efficiency. In this study, fine mesh was used in the vicinity of the loading area whereas coarse mesh was used further away from the loading area. The fine and coarse mesh were connected by the gradient mesh. The element thickness was found to be critical for calculation accuracy. The selected element thickness is 0.1 m for the loading area and 0.2 m for the edge of the area.

2.3.3 Bonding and boundary conditions

In terms of boundary conditions, because the model is large enough, the boundary conditions will have no effect on the simulation results, so the four sides and the bottom surface are set as fixed constraints.

2.3.4 Loading conditions

The width of the wheel is 2.1 m and the ground width of the wheel in the forward direction and the roller is 20-30 cm; this study used 25 cm. Therefore, loading is periodic surface loading. Surface loading consists of two parts; the first part is the weight of the roller and the second part is the vibration force. According to the actual parameters of the roller presented in Table 2, the surface load that is caused by the weight of the roller is 107 kPa. Similarly, the surface loading caused by the vibration force is 11.4 kPa and the angular velocity of the roller is 219.8 rad/s, or approximately 　　220 rad/s. Therefore, the periodic surface load applied is P=114+107sin220t kPa. Figure 2 shows the structure of the finite element model.

2.4 Orthogonal testing based on finite element numerical simulation

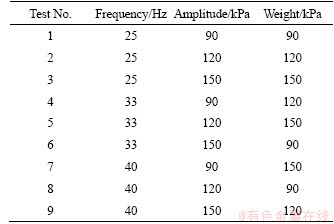
In this paper thus far, the subroutine of the finite element numerical simulation has been described and the dynamic changes of the strength indicators of the compacted materials used in the process of road compaction have been determined. In studying the effects of the different input parameters of the roller on compaction quality, each condition takes a long time to simulate. Therefore, an orthogonal test design is employed that uses three factors and three levels to explore the impact of various factors on compaction quality. Because the selected roller input parameters have three factors, each factor has three different variables. Therefore, the working conditions are comprised of 27 groups. Using this orthogonal test design, only nine sets of working conditions need to be calculated, which greatly improves the calculation efficiency.

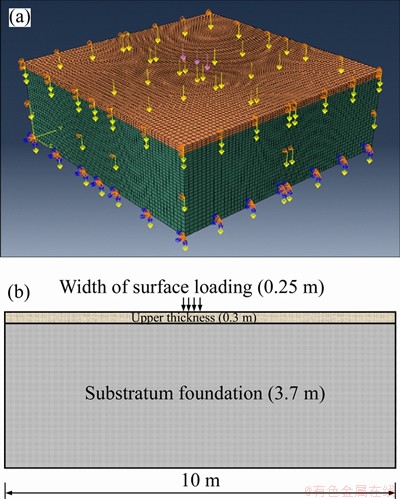
Figure 2 Finite element model (a) and subgrade structure (b)

Frequency, amplitude, and quality are the three factors that constitute the surface load input in the numerical simulation. Therefore, the three factors selected for this study likewise are frequency, amplitude, and quality. Each factor corresponds to three levels. Level 1 and Level 3 are the maximum and minimum values of most roller input parameters, whereas Level 2 adopts the interpolation method for selection. Thus, an orthogonal test table with three factors and three levels was established, as shown in Tables 3 and 4. They show that the selection of each level corresponds to each factor in the nine groups of the working conditions used in the orthogonal tests.

Table 3 Three factors and three levels of orthogonal test table

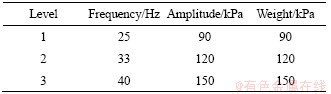
Table 4 Orthogonal test conditions

3 Results and analysis

The relationship between the degree of compaction and shear strength was obtained via laboratory tests. Based on the above numerical calculation, the dynamic response of the soil mass in the compaction process was determined, the displacement response, degree of compaction, and CMV change rules of the soil mass were extracted and analyzed, and a quality compaction control indicator, the AICV, was proposed. Through orthogonal testing and sensitivity analysis, the most important factor that affects compaction quality was obtained.

3.1 Results of laboratory direct shear tests

Figure 3 presents the relationship between vertical stress and shear strength under various degrees of compaction. The shear strength linearly increases with an increase in the degree of compaction as well as an increase in vertical stress.Additionally, the intersection point of each curve with the y-coordinate (shear strength) increases gradually with the increase in the degree of compaction, which indicates that the cohesive force c of the test specimens increases accordingly.

Based on the test results presented in Figure 3, the c and φ values of soil with different degrees of compaction were calculated. Under a certain degree of compaction, c is the value of the y-coordinate when the x-coordinate is 0 in the direct shear test curve under the degree of compaction, and φ is the angle between the direct shear test curve and the x-axis at a certain degree of compaction.

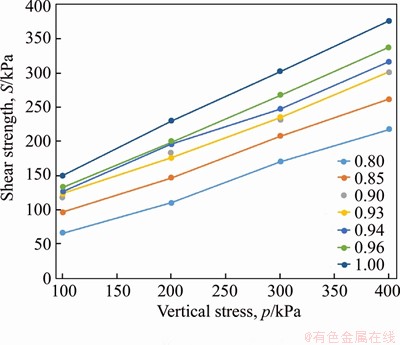
Figure 3 Relationship between shear strength and vertical stress

Also, the cohesion increases with an increase in the degree of compaction and cohesion is also the same. Figure 4 shows the fitted results for the degree of compaction K with cohesion c and friction angle φ.

3.2 Analysis of displacement response and degree of compaction during compaction

A roadway can be regarded as a semi-infinite space; therefore, the displacement of its horizontal plane (XOY) changes little and can be ignored under the action of vibration compaction. The change in vertical displacement, U₃, is used to represent the degree of compaction.

Compaction K can be calculated according to K=ρ/ρ_max. Of these values, ρ=m/V and ρ_max=m/V_min, so the degree of compaction K also can be calculated according to K=V_min/V. Considering the model as a semi-infinite space, X and Y remain unchanged. Therefore, the degree of compaction K can be characterized by vertical displacement U₃: K=U_3min/U₃.

Note: V_min is the volume at the maximum degree of compaction. V is the real-time volume during the compaction process.

Thus, the relationship between vertical cumulative displacement and time can be obtained through numerical simulation, and the relationship between degree of compaction and time can be obtained through the above calculation also, as shown in Figure 5. This figure indicates the phenomena that occur during the following stages.

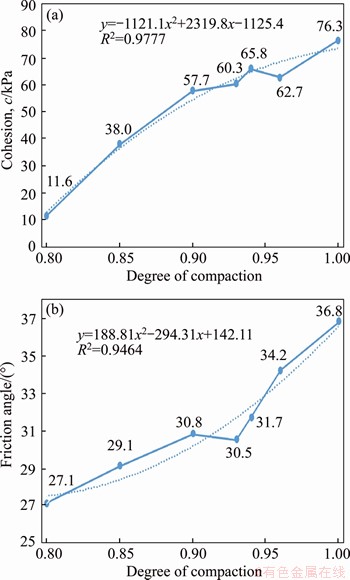
Figure 4 Degree of compaction-cohesion curve (a) and degree of compaction-friction angle curve (b)

1) In the first stage, the vertical displacement increases rapidly by about 1 cm. At the same time, the degree of compaction also increases rapidly,from the initial 0.8 to about 0.85. This phenomenon occurs because at the moment the roller contacts the soil, the weight of the roller will be at a certain degree of compaction of the soil. This part of the deformation is referred to as the static compaction depth.

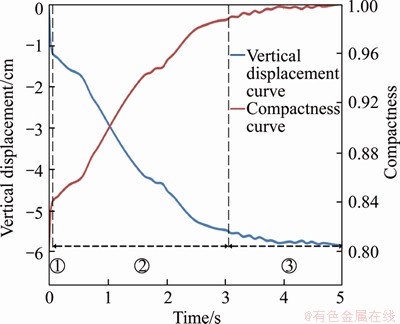
Figure 5 Displacement and degree of compaction of compacted soil

2) In the second stage, the vertical displacement of the soil is uniform and increases linearly, as does the degree of compaction of the soil. At the end of the second stage, the vertical displacement of the soil reaches 5.5 cm and the corresponding degree of compaction has exceeded 98%. The process of soil compaction occurs mainly in this stage. Also in this stage, the roller compacts the soil particles by vibration so that the pores of the soil are reduced and the degree of compaction of the soil is increased.

3) In the third stage, the vertical displacement tends to be stable to 5.9 cm; that is, 5.9 cm is the final displacement of the soil mass. However, the degree of compaction gradually increases to the maximum degree of compaction. In addition, in this model, the initial degree of compaction is 0.8, the soil thickness is 30 cm, and the expected settlement is 6 cm, which is close to the numerical calculation result of 5.9 cm. This outcome indicates that the amount of vertical settlement calculated by the numerical calculation is reasonable.

3.3 Analysis of compaction quality evaluation index

The CMV is based on the vertical acceleration of the vibration wheel and takes into account the diameter, weight, frequency, amplitude, and other factors that affect the compaction quality of the vibration wheel, which is a common evaluation indicator for the compaction quality of roadbeds and pavements. The CMV equation is shown here as Eq. 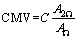(9).

                            (9)

where A_Ω is the amplitude of the fundamental frequency of the vibration wave in the acceleration of the vibration wheel; A_2Ω is the amplitude of the second harmonic component in the acceleration vibration wave of the vibration wheel; C is the constant coefficient.

Given the correlation between the CMV and settlement, the settlement analysis results show that the soil settlement changes most significantly in the first three seconds. The CMV and settlement also can reflect the compaction quality of the roadbed. In addition, the calculation of the CMV is based on a certain amount of data. If the amount of data is too small, the calculation of the CMV is not accurate. If the amount is too large, then fewer time domain segments will correspond to the CMV, leading to a decrease in the number of CMVs and an increase in the instability of the analysis results. Therefore, the CMV was calculated and analyzed for the first three seconds and every 0.5 s; thus, the CMV was calculated six times.

During the numerical calculation, the acceleration signal is extracted and the time domain signal is converted to the frequency domain signal by discrete fast Fourier transform in MATLAB. The CMV is calculated according to Eq. (9), as shown in Figure 6, which indicates the following.

1) The CMV has a certain volatility, but the overall trend is that the CMV increases with compaction because when the degree of compaction reaches a certain level, the compacted material will increase its resistance to the vibration wheel. This resistance is unstable and affects the acceleration signal together with the vibration force. Therefore, the acceleration signal will be disturbed within a certain range. This phenomenon is in good agreement with field test results [33-39].

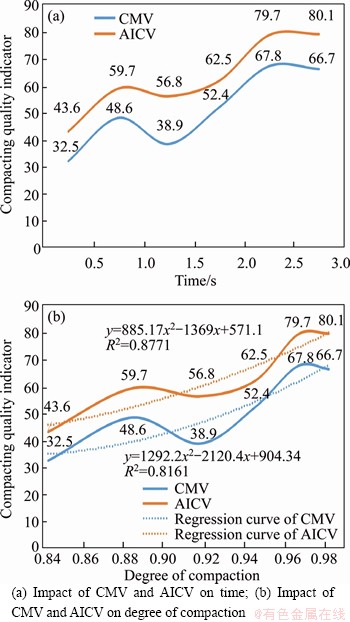
Figure 6 Comparison of CMV and AICV curves:

2) A temporary drop in the CMV occurred between 1 and 1.5 s. This occurrence is a common problem with the CMV. That is, at some point, no one-to-one relationship with the degree of compaction is present because the third or higher harmonic appears in the frequency domain as the degree of compaction increases, and the CMV does not take higher harmonics into account. In addition, the CMV is calculated by picking the acceleration signal over a period of time rather than at a particular point. The error associated with selecting the acceleration signal (such as not selecting a complete period) will cause calculation errors of the CMV. Therefore, the CMV generally is used to reflect the compaction quality roughly, but cannot accurately reflect the compaction quality.

Based on this information, a compaction quality evaluation indicator, the AICV with a third harmonic is proposed, which can be calculated using Eq. 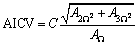(10).

                  (10)

Figure 4 presents comparison curves between the CMV and AICV, which shows the impact of the CMV and AICV on the degree of compaction. Figure 4 indicates the following.

1) The overall trend of both the CMV and AICV is consistent. Although the degree of compaction increases, the CMV and AICV show an overall growth trend. In the interval of 1 s to 1.5 s, both the CMV and AICV show a temporary decrease.

2) The CMV and AICV are fitted by a quadratic polynomial, and the AICV has the higher fitting degree, which is reflected mainly in the lower disturbance of the AICV between 1 and 1.5 s when the acceleration signal appears. When the degree of compaction reaches a certain level, the acceleration signal disturbance will lead to the frequency domain in the third or even higher harmonic. The AICV value takes the third harmonic into account in the compaction quality evaluation index, so it reduces the disorder degree of the compaction quality evaluation index.

3) Compared with the CMV’s correlation coefficient of 0.8161, the correlation between the AICV and degree of compaction is 0.8771, indicating that the AICV correlates better with the degree of compaction than the CMV.

3.4 Sensitivity analysis of influential factors of compaction quality

Using the numerical simulation method, the corresponding acceleration responses of the nine groups of orthogonal tests presented in Table 5 can be obtained. In this study, the CMV and AICV were selected as the evaluation indices for compaction quality. Specifically, the CMV and AICV within 5 s (calculated once every 0.5 s) were selected as the indices for compaction quality evaluation. Using the fast Fourier transform mentioned earlier, the averages of the CMV and AICV that correspond to each group of tests were obtained.

Based on Table 5, range analysis was adopted to analyze the main control factors of the compaction quality evaluation indices, the CMV and AICV. The analysis protocol is as follows. m_ij is assumed to be the sum of the factor i level j, and 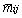is the average of m_ij.reflects the effect of factor i on the CMV or AICV, andmagnitude is expressed in range R_i, where 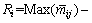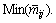The larger the R_j value, the greater the effect of this factor on the CMV or AICV. The factor that corresponds to Max(R_j) is the most important factor and the factor that corresponds to Min(R_j) is the least influential among all the factors.

Tables 6 and 7 present the range analysis results of the orthogonal tests and indicate the following.

1) The R_j values of the frequency, amplitude, and weight gradually decrease, so the effects of frequency, amplitude, and weight on the CMV and AICV likewise gradually decrease.

Table 5 CMV and AICV for each group of tests

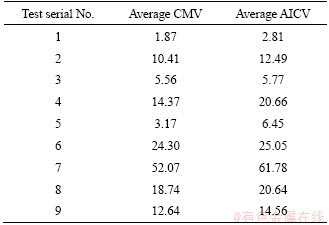
Table 6 CMV range analysis table of orthogonal tests

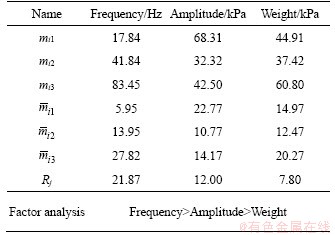
Table 7 AICV range analysis table of orthogonal tests

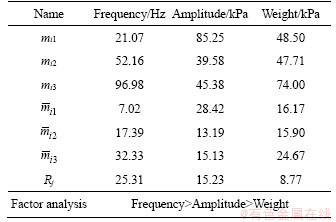
2) The R_j of the frequency and amplitude are greater than the R_j of weight, which shows that frequency and amplitude have a significant effect on the CMV and AICV.

Figure 7 shows the trends for the effect of each factor on the CMV and AICV and indicates the following.

1) Within the roller working range parameter, the CMV and AICV show consistency. Frequency is the most significant factor. Compaction quality is positively related to frequency; that is, compaction quality increases with an increase in frequency and decreases with a decrease in frequency.

2) Within the roller working range parameter, the responses of amplitude and weight to compaction quality are not simply linear, but the CMV and AICV first decrease and then increase with an increase in amplitude or frequency.

3) Within the roller working range parameter, the most effective way to increase or decrease the compaction quality is to adjust the frequency of the roller.

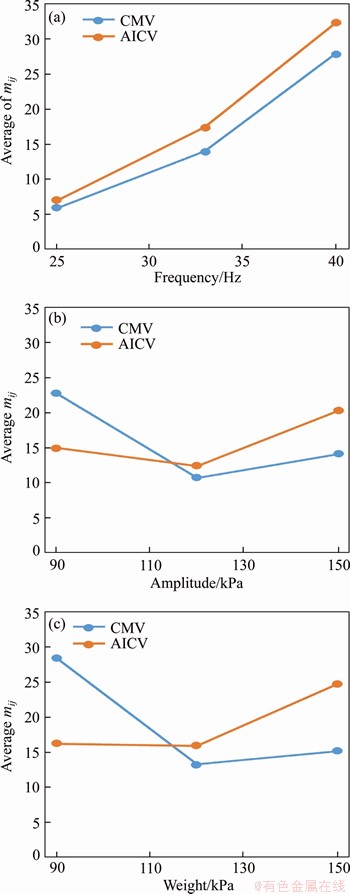
Figure 7 Trends of influential factors on CMV and AICV

4 Conclusions

Based on real-time changes of the mechanical parameters of the soil mass in an intelligent compaction process, intelligent compaction numerical calculations were carried out in this study and the following conclusions can be drawn.

1) Through theoretical derivations and laboratory tests, the relationship between the degree of compaction K and strain, and the relationship between the degree of compaction K and each of the soil strength indicators, c and φ, were established. The real-time variations of the soil strength indicators during the compaction process also were determined.

2) The numerical results show that displacement increases rapidly during the initial stage of compaction and that the displacement changes are relatively uniform and gradually tend to stabilize at 5.9 cm. This result is close to the experimental hypothesis value of 6 cm, which verifies the accuracy of the numerical results.

3) In this paper, the AICV compaction quality evaluation index is proposed, which takes into account the effect of the third harmonic. The accuracy of the AICV is better than that of the CMV.

4) Frequency is the most important factor that affects compaction quality. During the compaction process, compaction quality should first be controlled by adjusting the frequency.

Attributor

The authors confirm contributions to the paper as follows. Study conception and design: ZHANG Wei-guang and ZHANG Yu-qing; data collection: MA Yuan; analysis and interpretation of results: MA Yuan and LUAN Ying-cheng; draft manuscript preparation: MA Yuan, LUAN Ying-cheng; draft revision: ZHANG Wei-guang, ZHANG Hui. All authors reviewed the results and approved the final version of the manuscript.

References

[1] XU Qin-wu, CHANG G K. Evaluation of intelligent compaction for asphalt materials [J]. Automation in Construction, 2013, 30: 104-12. DOI: 10.1016/j.autcon. 2012.11.015.

[2] XU Qin-wu, CHANG G. K, GALLIVAN V L. Development of a systematic method for intelligent compaction data analysis and management [J]. Construction and Building Materials, 2012, 37: 470-480. DOI: 10.1016/j.conbuildmat. 2012.08.001.

[3] VENNAPUSA P K R, WHITE D J, SCHRAM S. Roller-integrated compaction monitoring for hot-mix asphalt overlay construction [J]. Journal of Transportation Engineering, 2013, 139: 1164-1173. DOI: 10.1061/(ASCE) TE.1943-5436.0000602.

[4] Intelligent Compaction Website. What is intelligent compaction in learn ICT in 2011: America [EB/OL]. http://www.intelligentcompaction.com.

[5] ZHAO Xiao-ping. Study on intelligent compaction control technology of subgrade [D]. Xi’an: Changan University, 2016. (in Chinese)

[6] MOONEY M A, GORMAN P B, GONZALEZ J N. Vibration based health monitoring during earthwork construction [J]. Journal of Structural Health Monitoring, 2005, 2(4): 137-152.

[7] MINCHIN R E, THOMAS H R. Validation of vibration- based onboard asphalt density measuring system [J]. Journal of Construction Engineering and Management, 2003, 129: 1-7. DOI: 10.1061/(ASCE)0733-9364(2003)129:1(1).

[8] CAI Hu-bo, KUCZEK T, DUNSTON P S, LI Shuai. Intelligent compaction data to in situ soil compaction quality measurements [J]. Journal of Construction Engineering and Management, 2017, 143(8): 04017038. DOI: 10.1061/(ASCE)CO.1943- 7862.0001333.

[9] WHITE D J, THOMPSON M J. Relationships between in situ and roller integrated compaction measurements for granular soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134: 1763–1770. DOI: 10.1061/(ASCE)1090-0241(2008)134:12(1763).

[10] LING Jian-ming, LIN Sheng, QIAN Jin-song. Continuous compaction control technology for granite residual subgrade compaction [J]. Journal of Materials in Civil Engineering, 2018, 30(12): 04018316. DOI: 10.1061/(ASCE)MT.1943- 5533.0002522.

[11] HU Wei, SHU Xiang, JIA Xiao-yang. Geostatistical analysis of intelligent compaction measurements for asphalt pavement compaction [J]. Automation in Construction, 2018, 89: 162-169. DOI: 10.1016/j.autcon.2018.01.012.

[12] THOMPSON M J, WHITE D J. Field calibration and spatial analysis of compaction-monitoring technology measurements [J]. Transportation Research Record Journal of the Transportation Research Board, 2007, 2004: 69-79. DOI: 10.3141/2004-08.

[13] WHITE D J, VENNAPUSA P K R, GIESELMAN H H. Field assessment and specification review for roller- integrated compaction monitoring technologies [J]. Advances in Civil Engineering, 2011(2): 1-15. DOI: 10.1155/2011/ 783836.

[14] ZHANG Yao, MA Tao, LING Meng, ZHANG De-yu, HUANG Xiao-ming. Predicting dynamic shear modulus of asphalt mastics using discretized- element simulation and reinforcement mechanisms [J]. Journal of Materials in Civil, 2019, 31(8). DOI: 10.1061/ (ASCE)MT.1943-5533.0002831.

[15] ZHANG Yao, MA Tao, DING Xun-hao, HUANG XIAO-ming, XU Guang-ji. Impacts of Air-void structures on the rutting tests of asphalt concrete based on discretized emulation [J]. Construction and Building Materials, 2018, 166: 334-344. DOI: 10.1016/ j.conbuildmat.2018.01.141.

[16] CHEN Tian, LUAN Ying-cheng, MA Tao, ZHU Jun-qing, HUANG Xiao-ming, MA Shi-jie. Mechanical and microstructural characteristics of different interfaces in cold recycled mixture containing cement and asphalt emulsion [J]. Journal of Cleaner Production, 2020, 258. DOI: 10.1016/j.jclepro.2020.120674.

[17] MA Tao, WANG Hao, ZHANG De-yu, ZHANG Yao. Heterogeneity effect of mechanical property on creep behavior of asphalt mixture based on micromechanical modeling and virtual creep test [J]. Mechanics of Materials, 2017, 104: 49-59. DOI: 10.1016/j.mechmat.2016.10.003.

[18] TANG Fan-long, MA Tao, ZHANG Jun-hui. Integrating three-dimensional road design and pavement structure analysis based on BIM [J]. Automation in Construction, 2020, 113: 103152. DOI: 10.1016/j.autcon.2020.103152.

[19] ZHANG Yao, MA Tao, LING Meng, HUANG Xiao-ming. Mechanistic sieve-size classification of aggregate gradation by characterizing load-carrying capacity of inner structures [J]. Journal of Engineering Mechanics, 2019, 145(9). DOI: 10.1061/(ASCE)EM.1943-7889.0001640.

[20] JTG E40-2007: Test methods of soils for highway engineering, China [S]. (in Chinese)

[21] MA Tao, ZHANG De-yu, ZHANG Yao, WANG Si-qi. Simulation of wheel tracking test for asphalt mixture using discrete element modelling [J]. Road Materials and Pavement Design, 2018, 19: 367-384. DOI: 10.1080/ 14680629.2016.1261725.

[22] DING Xun-hao, MA Tao, HUANG Xiao-ming. Discrete- element contour-filling modeling method for micro-and micromechanical analysis of aggregate skeleton of asphalt mixture [J]. Journal of Transportation Engineering, Part B: Pavements, 2019, 145(1): 04018056. DOI: 10.1061/JPEODX.0000083.

[23] DING Xun-hao, CHEN Lu-chuan, MA Tao, MA Hai-xia, GU Lin-hao, CHEN Tian, MA Yuan. Laboratory investigation of the recycled asphalt concrete with stable crumb rubber asphalt binder [J]. Construction and Building Materials, 2019, 203: 552-557. DOI: 10.1016/j.conbuildmat. 2019.01.114.

[24] TANG Fan-long, MA Tao, GUAN Yong-sheng, ZHANG Zhi-xiang. Parametric modeling and structure verification of asphalt pavement based on BIM-ABAQUS [J]. Automation in Construction, 2020, 111: 103066. DOI: 10.1016/j.autcon. 2019. 103066.

[25] DING Xun-hao, MA Tao, GU Lin-hao, ZHANG De-yu, HUANG Xiao-ming. Discrete element methods for characterizing the elastic behavior of the granular particles [J]. Journal of Testing and Evaluation, 2020, 48(3): 20190178. DOI: 10.1520/JTE20190178.

[26] ZHANG Wei-guang, AKBER M A, HOU Shu-guang, BIAN Jiang, ZHANG Dong, LE Qi-qi. Detection of dynamic modulus and crack properties of asphalt pavement using a non-destructive ultrasonic wave method [J]. Apply Science, 2019, 9(15): 2946. DOI: 10.3390/ app9152946.

[27] XIA Wei-yi, DU Yan-jun, LI Fa-sheng, LI Chun-ping, YAN Xiu-lan, ARUL A, WANG Fei, SONG De-jun. In-situ solidification/stabilization of heavy metals contaminated site soil using a dry jet mixing method and new hydroxyapatite based binder [J]. Journal of Hazardous Materials, 2019, 369: 353-361. DOI: 10.1016/j.jhazmat.2019.02.031.

[28] XIA Wei-yi, FENG Ya-song, JIN Fei, ZHANG Li-ming, DU Yan-jun. Stabilization and solidification of a heavy metal contaminated site soil using a hydroxyapatite based binder [J]. Construction and Building Materials, 2017, 156: 199-207. DOI: 10.1016/ j.jhazmat.2019.02.031.

[29] WU Hao-liang, JIN Fei, BO Yun-lin, DU Yan-jun, ZHENG Jun-xing. Leaching and microstructural properties of lead contaminated kaolin stabilized by GGBS-MgO in semi-dynamic leaching tests [J]. Construction and Building Materials, 2018, 172: 626-634. DOI: 10.1016/j.conbuildmat.2018.03.164.

[30] JIANG Ning-jun, DU Yan-jun, LIU Kai. Durability of lightweight alkali-activated ground granulated blast furnace slag (GGBS) stabilized clayey soils subjected to sulfate attack [J]. Applied Clay Science, 2018, 161: 70-75. DOI: 10.1016/j.clay.2018.04.014.

[31] LIU Guo-qiang, YANG Tao，LI Jing, JIA Yan-shun, ZHAO Yong-li, ZHANG Jun-peng. Effects of aging on theological properties of asphalt materials and asphalt-filler interaction ability [J]. Construction and Building Materials, 2018, 168: 501-511. DOI: 10.1016/ j.conbuildmat.2018.02.171.

[32] CHEN An-qi, LIU Guo-qiang, ZHAO Yong-li, LI Jing, PAN Yuan-yuan, ZHOU Jian. Research on the aging and rejuvenation mechanisms of asphalt using atomic force microscopy [J]. Construction and Building Materials, 2018, 167: 177-184. DOI: 10.1016/ j.conbuildmat.2018.02.008.

[33] MA Tao, WANG hao, HE Liang, ZHAO Yong-li, HUANG Xiao-ming, CHEN Jun. Property characterization of asphalt and mixtures modified by different crumb rubbers [J]. Journal of Materials in Civil Engineering, 2017, 29(7): 1-10. DOI: 10.1061/(ASCE)MT. 1943-5533.0001890.

[34] MA Tao, ZHANG De-yu, ZHANG Yao, WANG Si-qi, HUANG Xiao-ming. Simulation of wheel tracking test for asphalt mixture using discrete element modelling [J]. Road Materials and Pavement Design, 2018, 19(2): 367-384. DOI: 10.1080/14680629.2016.1261725.

[35] ZHANG Jun-hui, DING Le, LI Feng, PENG Jun-hui. Recycled aggregates from construction and demolition wastes as alternative filling materials for highway subgrades in China [J]. Journal of Cleaner Production, 2020, 255: 120223. DOI: 10.1016/ j.jclepro.2020.120223.

[36] ZHANG Jun-hui, PENG Jun-hui, LIU Wei-zheng, LU Wei-hua. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction [J]. Road Materials and Pavement Design, 2019, 1: 1-13. DOI: 10.1080/ 14680629.2019.1651756.

[37] ZENG Ling, XIAO Liu-yi, ZHANG Jun-hui, PENG Jun-hui. The role of nanotechnology in subgrade and pavement engineering: A review [J]. Journal of Nanoscience and Nanotechnology, 2020, 255120223. DOI: 10.1016/j.jclepro. 2020.120223.

[38] YU Hua-nan, SHEN Shi-hui, QIAN Guo-ping, GONG Xiang-bing. Packing theory and volumetrics-based aggregate gradation design method [J]. Journal of Materials in Civil Engineering, 2020. 32(6): 04020110. DOI: 10. 1061/(asce) mt.1943-5533.0003192.

[39] YU Hua-nan, HE Zhi-yu, QIAN Guo-ping, GONG Xiang-bing, QU Xiang. Research on the anti-icing properties of silicone modified polyurea coatings (SMPC) for asphalt pavement [J]. Construction and Building Materials, 2020, 242, 117793. DOI: 10.1016/ j.conbuildmat.2019.117793.

(Edited by HE Yun-bin)

中文导读

路基智能压实技术的数值仿真

摘要：在路基压实过程中，土体的力学参数是实时变化的，但在目前的研究中，假设这些参数保持不变。为了解决这一矛盾，本文建立了压实度K和应变ε之间的关系，并通过室内实验得到压实度K与土体的抗剪强度(黏聚力c和摩擦角φ)之间的关系。为了实现路基压实质量的精确计算，对ABAQUS有限元数值软件进行了二次开发。将数值仿真的结果与模型假定的压实值进行对比分析，验证了路基土智能压实计算结果的准确性。在此基础上，对影响压实度的因素进行了正交试验和敏感度分析。最后，针对精度较差的压实质量评价指标，提出了更为精确的压实质量评价指标。研究结果可为进一步研究路基路面压实质量的准确控制提供指导和依据。

关键词：智能压实；数值模拟；动态变化；指标；正交试验

Foundation item: Project(51878164) supported by the National Natural Science Foundation of China; Projects(BK20161421, BK20140109) supported by the Natural Science Foundation of Jiangsu Province, China; Project(141076) supported by the Huoyingdong Foundation of the Ministry of Education of China; Project(BZ2017011) supported by the Science and Technology Support Project of Jiangsu Province, China; Project(2242015R30027) supported by the Fundamental Research Funds for the Central Universities, China; Project(grant number KFJ170106) supported by the Changsha University of Science & Technology via Open Fund of National Engineering Laboratory of Highway Maintenance Technology, China; Project(2018B51) supported by the Science and Technology Support Project of Qilu Transportation Development Group, China

Received date: 2020-03-25; Accepted date: 2020-06-23

Corresponding author: ZHANG Wei-guang, PhD, Associate Professor; Tel: +86-13912956989; E-mail: wgzhang@seu.edu.cn; ORCID: 0000-0002-3323-5557