
J. Cent. South Univ. (2021) 28: 2131-2139
DOI: https://doi.org/10.1007/s11771-021-4664-3

Channel aware receiver for next generation wireless communication system
MUHAMMAD Asim, ASFANDYAR Khan, JAVED Iqbal Bangash, ABDULLAH Khan
Department of Computer Science and Information Technology, ICS/IT, FMCS,The University of Agriculture, Peshawar, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: We consider an iterative phase synchronization scheme based on maximum a posteriori probability algorithm. In classical approaches, the phase noise estimation model considers one sample per symbol at the channel and receiver. However, information theoretic studies suggested use of more than one sample per symbol at the channel and receiver for achieving higher performance. In this article, a soft-information aided iterative receiver is derived, which uses off-the-shelf blocks for detection and demodulation by keeping the complexity of the receiver acceptable. We consider here two samples per symbols at the channel and receiver in a pragmatic paradigm. It is shown that phase noise estimation can be significantly improved at the expense of modest processing overhead. Simulation results are presented for low-density parity check coded quadrature amplitude modulations. Our results show a significant performance improvement for strong phase noise values compared to classical receiver approaches.
Key words: phase noise channel; iterative receiver; multi-sample; LDPC coded modulations
Cite this article as: MUHAMMAD Asim, ASFANDYAR Khan, JAVED Iqbal Bangash, ABDULLAH Khan. Channel aware receiver for next generation wireless communication system [J]. Journal of Central South University, 2021, 28(7): 2131-2139. DOI: https://doi.org/10.1007/s11771-021-4664-3.
1 Introduction
Burgeoning demand to provide greater information capacity with spectrally efficient communication systems has made significant progress with the advent of newer communication techniques. To meet the ever increasing demand for spectral efficiency in the next generation wireless communication, the carrier synchronization plays a pivotal role. The main task of the carrier synchronization is to synchronize the local oscillators at the receiver with the incoming carrier signal for both frequency and phase terms. Commonly, phase lock loop (PLL) is used to perform carrier synchronization, where their performance for phase noise is not very essential [1]. The presence of phase noise causes distortion or complete loss of information in traditional receivers and, consequently, high bit error rate (BER).
A common phase noise channel model assumes additive white Gaussian noise (AWGN) channel with slowly varying phase noise over one sample per symbol duration [2] and is commonly known as symbol-time model. In this model, the samples at the channel and receiver are defined over one sample per symbol-time [3]. In a multi-sample communication system, we consider an AWGN channel with phase noise over more than one sample per symbol-time duration, where samples at the channel and receiver are characterized with more than one sample per symbol-time and are referred here as “sample-time” model [4].
Many techniques for phase synchronization have been proposed mostly focusing on a phase noise channel having no inter-symbol interference (ISI) with varieties of detection/decoding schemes as in Ref. [5] and references therein. A theoretical analysis using binary offset carrier pulse shape in a multi-sample phase noise channel is performed [6], whereas with higher complexities, the joint detection and decoding in an oversample environment have shown higher performance [7, 8]. The multi-sample per symbol inherently adds a well-known transmission impairment known as ISI. To calculate the a posteriori probability (APP) of the symbols from the ISI channel, Bahl-Cocke- Jelinek-Raviv (BCJR) algorithms can be used. However, the BCJR algorithms are not feasible for a longer ISI channel, larger constellation sizes and greater sampling rates [9]. From an implementation point of view, soft ISI cancellation and detection in block-processing fashion can be regarded as more attractive solution for any modulation, ISI channels and sampling rates [10]. Further enhancement like using improvement log likelihood ratios (LLRs) can increase the performances of the proposed systems as in Refs. [11-13] and can be a subject of future work.
In this paper, we derive a channel model in the presence of phase noise for sample-time model. We exploit the received multiple samples from the channel in an iterative fashion to compensate the phase noise and cancel the ISI to achieve robust convergence. We design an iterative phase synchronization algorithm based on maximum a posteriori probability (MAP), which uses the APPs of the transmitted symbols for phase noise estimation. It is shown that the proposed multi- sample receiver achieves significant performance improvement for QAM modulations.
The remainder of the paper is organized as follows. Section 2 discusses the system models for the considered setup with phase noise characteristics. In Section 3, the proposed iterative receiver for phase synchronization is presented. A brief discussion on iterative receiver operation is presented in Section 4. Section 5 and Section 6 demonstrate the simulation results and conclude the paper, respectively.
2 System characteristics
Figure 1 shows the continuous-time phase noise impaired channel. The signal received at the front-end filter is given by
 (1)
(1)
where 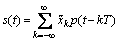 is the signal being transmitted, where
is the signal being transmitted, where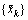 is the modulated symbol shaped by a unit-energy pulse shape p(t). A low density parity check (LDPC) coded sequence {ak} is used in quadrature amplitudes modulation (QAM) symbols
is the modulated symbol shaped by a unit-energy pulse shape p(t). A low density parity check (LDPC) coded sequence {ak} is used in quadrature amplitudes modulation (QAM) symbols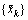 at T time-spacing and shaped by root raised cosine (RRC) pulse shape having a roll-off factor
at T time-spacing and shaped by root raised cosine (RRC) pulse shape having a roll-off factor The wireless communication channel adds AWGN n(t) and phase noise. The baseband complex output of the local oscillator can be expressed by
The wireless communication channel adds AWGN n(t) and phase noise. The baseband complex output of the local oscillator can be expressed by and is modeled by random Wiener process generated by integrating a white Gaussian noise process with power spectral density 2πBθ. The random Wiener process is nonstationary and phasor
and is modeled by random Wiener process generated by integrating a white Gaussian noise process with power spectral density 2πBθ. The random Wiener process is nonstationary and phasor has a Lorentzian spectrum with 3-dB spectral width Bθ.
has a Lorentzian spectrum with 3-dB spectral width Bθ.
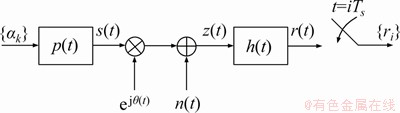
Figure 1 A typical continuous-time phase noise channel model
As we know that the RRC pulses have linear phase response and they satisfy the Nyquist criterion resulting no ISI. A front-end filter h(t) is used at reception, which is defined as a convolution of the transmitted pulse with channel response having filter bandwidth Bh and frequency response H(f), such that
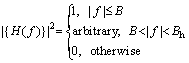 (2)
(2)
Note that the signal bandwidth for the RRC band-limited pulse shapes is strictly limited to B=(1+β)/2T.
The useful signal is not attenuated by the front-end filter due to the unitary frequency response in the bandwidth. As the frequency response |H(f)|2 in Eq. (2) has a vestigial symmetry with respect to 1/2Ts, multiple samples at Ts instant result in an independent and identically distributed (IID) samples. The sampling of the received sequence ri at period Ts<1/2Bh after front-end filter is a sufficient statistic [14]. To simplify the operation, we consider Ts a function of T, such that Ts=T/Nu, where Nu is the oversampling factor.
In particular, the QAM symbols are generated by using coded information sequence {cj} through an LDPC channel coding scheme with coding rate R. Here, we consider LDPC coded modulation with 16-QAM signaling having size M=2b and symbol energy Es. In another case, we consider multi-level coding (MLC) [15] scheme for 64-QAM modulation such that b-b1 are coded and b1 is left uncoded. Note that the proposed scheme relies on the soft-information of the detection/ decoding part, so any coding/demodulation scheme can be easily integrated.
are generated by using coded information sequence {cj} through an LDPC channel coding scheme with coding rate R. Here, we consider LDPC coded modulation with 16-QAM signaling having size M=2b and symbol energy Es. In another case, we consider multi-level coding (MLC) [15] scheme for 64-QAM modulation such that b-b1 are coded and b1 is left uncoded. Note that the proposed scheme relies on the soft-information of the detection/ decoding part, so any coding/demodulation scheme can be easily integrated.
Pilot (known) symbols in the transmitted frames are used to perform initial phase synchronization. A number Np of pilot symbols having symbol energy Ep are used from a QPSK modulations and placed in every N consecutive number of data symbols. Here we define  which is a ratio between the pilot and data symbol energies. The average data symbol energy can be expressed as
which is a ratio between the pilot and data symbol energies. The average data symbol energy can be expressed as
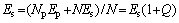
where the factor (1+Q) can be regarded as the energy loss due to the insertion of pilot symbols in the data.
As shown in Figure 1, a block diagram of continuous-time phase noise channel, after front-end filtering the received signal r(t) is sampled at Tstime instant. The samples ri can be written as:
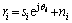 (3)
(3)
with
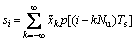

where xn is obtained by interpolating the 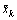 with zeros, which can be expressed as:
with zeros, which can be expressed as:
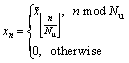
in which 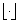 denotes the floor function used to take the greatest integer less than or equal to the argument and Eq. (3) is given by
denotes the floor function used to take the greatest integer less than or equal to the argument and Eq. (3) is given by

The RRC filter pn can be defined over an infinite length, so we assume here a finite length filter in which only the significant L filter terms are used, where L=2v+1 to avoid any energy and memory constraints [16], such that
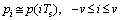 (4)
(4)
Received samples at the i-th instant can be given by
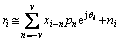 (5)
(5)
In Eq. (5), the θi can be regarded as discrete-time phase noise, which can be modeled as Wiener phase noise process, where
θi=θi-1+△i mod 2π (6)
where △i~N 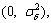 where
where 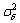 =2πBθTs is the variance at a given Ts sample time. The symbol-time phase noise process can be defined at instant T and can be expressed as:
=2πBθTs is the variance at a given Ts sample time. The symbol-time phase noise process can be defined at instant T and can be expressed as:
θk=θk-1+△k mod 2π (7)
where △k~N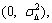 with
with 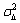 =Nu
=Nu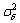 =2πBθTs.
=2πBθTs.
The received signal in Eq. (5) after matched-filtering can be represented as:

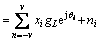 (8)
(8)
given 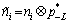 is an AWGN process with variance
is an AWGN process with variance and
and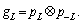 Note that the symbol and sample time as discussed in Eq. (7) can be related by
Note that the symbol and sample time as discussed in Eq. (7) can be related by 
Considering a slowly varying phase noise with matched filtering, the traditional receiver with sampling at kTs, i.e., sampling at symbol time, can be expressed as follows:
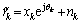 (9)
(9)
which is a common phase noise estimation model. The received energy per information bit can be defined as  and the SNR γb is given by
and the SNR γb is given by
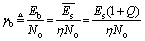 (10)
(10)
3 Phase synchronization receiver
Initially, we consider the iterative MAP based phase noise estimation strategies in Ref. [2], which is based on the symbol time phase noise process discussed in Eq. (9).
3.1 Phase synchronization at symbol-time
The phase noise is assumed to be constant for a given consecutive received symbols refer to as an observation window of length  and such schemes are known as block-window (BW) phase noise estimation. Note that observation window is assumed to sufficiently short compared to data being transmitted. In BW algorithm, we use disjoint observation windows for given symbols. For example, the k-th symbol belongs to the
and such schemes are known as block-window (BW) phase noise estimation. Note that observation window is assumed to sufficiently short compared to data being transmitted. In BW algorithm, we use disjoint observation windows for given symbols. For example, the k-th symbol belongs to the  window block having length d, and the following k-th disjoint windows i.e., k=d
window block having length d, and the following k-th disjoint windows i.e., k=d , d
, d +1, …, (d+1)
+1, …, (d+1) -1 will be used and the phase noise estimates can be given by
-1 will be used and the phase noise estimates can be given by
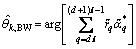 (11)
(11)
where 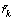 is the k-th received observable;
is the k-th received observable;  is obtained from APPs of the transmitted constellation some time referred as soft-symbol or center of gravity of the constellation at instant k; (·)* denotes the complex conjugate operation.
is obtained from APPs of the transmitted constellation some time referred as soft-symbol or center of gravity of the constellation at instant k; (·)* denotes the complex conjugate operation.
In another optimal approach, the sliding variant of the window based approach known as phasor linear prediction (PLP) is used. For given k-th received observable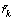 is related to
is related to overlapping observable windows that start from k-
overlapping observable windows that start from k- +1 and lasts till epoch k, such that Eq. (11) can be expressed as
+1 and lasts till epoch k, such that Eq. (11) can be expressed as
 (12)
(12)
where the following weights are used
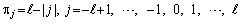 (13)
(13)
where πj are the weights having a triangular shape. For uniform weights during the phase noise estimation, some border management should be performed due to the nature of weights. Note that the phase noise estimation is performed on received observable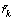 as in Eq. (9), which is obtained after matched filtering.
as in Eq. (9), which is obtained after matched filtering.
3.2 Phase synchronization at sample-time
From information theoretic perspective, the phase noise channel with more samples can improve the receiver performance. The proposed work is a step towards realizing the concept of multiple samples at the channel and receiver. From Eq. (8), we noticed that the received observable ri at the i-th instant is correlated with future and past samples [10]. In particular, ri consists of L=2v+1 samples as an input to the matched filter. The output of a matched filtering at the i-th instant can be represented by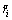 as shown in Figure 2. We have
as shown in Figure 2. We have
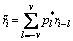 (14)
(14)
As to accurately perform phase noise estimation, we need to reconstruct signal received at the channel. Similarly, the soft-information aided signal is based on the received information. In order to keep the ISI minimum, we consider a received observable at the i-th instant, such that
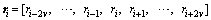
having a 2L-1 length.
The vector ri of the receiver samples can be process as
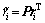 (15)
(15)
where (·)T is the transpose of the argument and P is a circular matrix of dimension L×(2L-1), which can be given by:

The corresponding soft symbols can be given by:
αi=[αi-2v, …, αi-1, αi, αi+1, …, αi+2v]
with length 2L-1. Similarly, we can perform processing using the APPs of the transmitted symbols with pulse shape in reconstructing the soft symbols, which can be expressed as follows:
 (16)
(16)
here G is also a circular matrix of dimension L×(2L-1) and can be expressed as:

in which 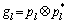 is the matched filter response of the shaping at sample-time with filter length L=2v+1 samples.
is the matched filter response of the shaping at sample-time with filter length L=2v+1 samples.
Finally, formulation in Eq. (12) can be used, such that at epoch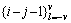 for a given observable, the received samples as in Eq. (15) and the soft symbols in Eq. (16) can be processed. Therefore, the l-th phase estimate with respect to l=-v,…, v, associated with the i-th sample can be written as
for a given observable, the received samples as in Eq. (15) and the soft symbols in Eq. (16) can be processed. Therefore, the l-th phase estimate with respect to l=-v,…, v, associated with the i-th sample can be written as
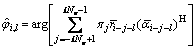 (17)
(17)
where πj are the weights having triangular shape as in Eq. (13) and (·)H is the Hermitian operator for argument. Finally, the phase estimates are obtained by averaging out the 2v+1 phase estimates in Eq. (17) such that
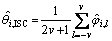 (18)
(18)
Due to nature of this scheme, we term it as inter-sample correlated (ISC) phase synchronization.
4 Iterative receiver
In Figure 2, an iterative structure of the proposed low-complexity receiver for sample time phase noise estimation is shown. The principle of operation of the receiver structure is described, which has following main components: (i) matched filtering (MF), (ii) linear interpolator (INT), (iii) demapper and soft-input soft-output (DEM/SISO) decoder block which consists of demodulation, and channel decoder. The soft-information from the demapper and decoder is used to perform phase noise estimation.
The receiver works in two modes. In the first mode, the processing is carried out in the sample-time. In the second mode, the symbol-time processing is performed solely to obtain the soft-information from the decoder to improve the accuracy of soft symbol αi and improve the phase accuracy of the received samples. Note that in traditional phase noise estimation approaches, the phase noise estimation is performed at symbol-time; however, this work proposes phase correction at sample-time, which can be regarded as a main contribution of this work.
Initially, ISI is reduced by performing matched filtering for the received observables followed by down sampling by a factor Nu to be fed for symbol-time processing. Linear interpolator will be used to perform the initial phase synchronization. Note that some advanced feed forward filtering such as Weiner filter can be employed with better performance; however, we consider linear interpolator due to its simple structure.
The interpolator operation relies on the information of the known consecutive pilot symbols placed between the transmitted data sequence. The estimated phase noise by the interpolator is the difference between the phase of the received and transmitted symbol, respectively. The observable after the interpolator processing can be denoted as 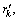 such that
such that
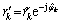 (19)
(19)
where 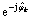 is the de-rotation introduced by the linear interpolator. Interpolator will be only operational for the first iteration of the receiver to obtain reliable APPs from the demodulator and detector. The remaining iterations will use ri directly for detection and phase noise estimation.
is the de-rotation introduced by the linear interpolator. Interpolator will be only operational for the first iteration of the receiver to obtain reliable APPs from the demodulator and detector. The remaining iterations will use ri directly for detection and phase noise estimation.
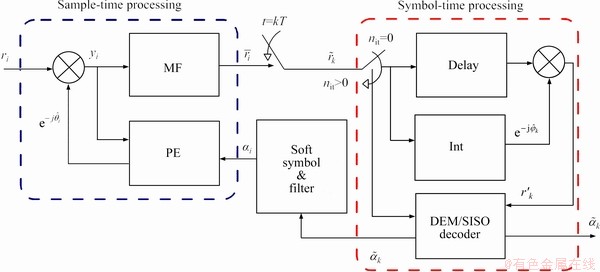
Figure 2 Systematic block diagram of iterative multi-sample phase noise estimation receiver
The output of the linear interpolator r′k is fed directly to soft demapper and decoder for obtaining reliable soft information in terms of bits. The log-likelihood ratios (LLRs) on the channel coded bits are used for APPs calculation on the transmitted constellation. The soft-symbols with pulse shape is then used to estimate the phase noise introduced by the channel.
The number of iterations can be expressed as n= 1, …, nit, where nit is the maximum number of iterations. After each phase noise estimation and compensation,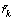 will be used for further processing for the generation of soft-information. At the n-th iteration, the phase estimator (PE) will perform phase noise compensation on the observables vector y[n]such that
will be used for further processing for the generation of soft-information. At the n-th iteration, the phase estimator (PE) will perform phase noise compensation on the observables vector y[n]such that
 (20)
(20)
where ri is the observable received from phase noise impaired channel, and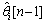 is the estimated phase noise at the n-th iteration. At each iteration, the observable y[n] is the derotated version of the ri, which is fed to the matched filtering and then to soft demodulator/decoder for the computation of the APPs of transmitted symbols as in Eq. (16). The estimated phase at each n-th iteration corresponds to phase estimated at the previous iteration and a residual phase error
is the estimated phase noise at the n-th iteration. At each iteration, the observable y[n] is the derotated version of the ri, which is fed to the matched filtering and then to soft demodulator/decoder for the computation of the APPs of transmitted symbols as in Eq. (16). The estimated phase at each n-th iteration corresponds to phase estimated at the previous iteration and a residual phase error 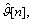 which can be given by
which can be given by
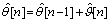 (21)
(21)
5 Simulation results
Finally, the performance of the proposed iterative receiver structure is presented in Figure 3. Multi-sample receiver system parameter settings have been shown in Table 1. LDPC coded QAM modulations are used with different levels of phase noise variances σ△. For 64-QAM modulation, an MLC scheme is adopted according to Ungerboeck set partitioning rules, and subsets are selected to maximize the Euclidean distance using a set partitioning [17]. Gray mapping, in terms of free bits, is used to label the points within a given subset [18]. We consider b-b1 LDPC coded bits whereas b1=2 is left uncoded. One pilot symbol is inserted i.e., Np=1 after every 48 data symbols, also referred to as pilot spacing. Every pilot symbol belongs to 4-QAM modulation having 2.5 times higher energy compared to the symbol energy of the respective QAM data symbols.
The performance of ISC multi-sample receiver is compared with an equivalent classical receiver using PLP approach presented in Ref. [2], using symbol-time channel model. In another approach, we used sample-time model, where two samples per symbol are available at the channel and only one sample at the receiver. We term it as PLP-matched filtering (PLP-MF) and as in this phase synchronization, the phase correction is performed after matched filtering. For our proposed receiver, we consider only two samples per symbol, i.e., Nu=2. From information theoretic studies as in Ref. [4], further performance improvement can be expected by increasing the sampling rate at the expense of additional overhead. We here consider two samples at the channel and at the receiver with RRC pulse shaping having a roll-off factor β=0.3 and L=2v+1=13. All the simulations are performed for nit=5 iterations, where the soft-decisions of the demodulator and detector are fed to the next iteration.
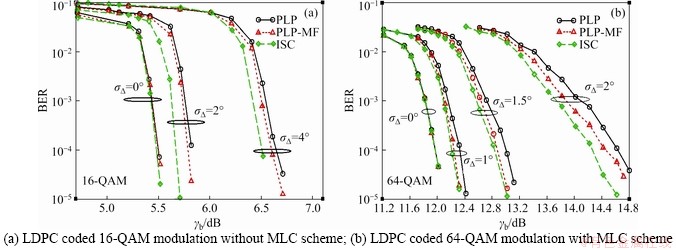
Figure 3 Bit error rate (BER) as a function of γb for phase noise impaired channel and different receiver structures:
Table 1 System parameter settings for simulation

All the phase noise estimation algorithms are analyzed with observation window length  symbols interval. This means that the ISC approach with Nu samples per symbols will have a window length of
symbols interval. This means that the ISC approach with Nu samples per symbols will have a window length of  Nu. Our simulation results not shown here demonstrate that
Nu. Our simulation results not shown here demonstrate that is an optimized window length for phase noise estimation for different values of phase noise σ△.
is an optimized window length for phase noise estimation for different values of phase noise σ△.
In Figure 3 (a), the BER is shown as a function of γb with different phase noise variances σ△ for LDPC coded 16-QAM modulation. Simulation results demonstrate that as we increase the values of the σ△, the performance of receiver starts degrading and at higher values σ△ the phase noise will be so much prominent that the receiver will not be able to recover the original information e.g., σ△=4°. In the considered scenarios, the symbol-time model which is denoted by “PLP” has the worst performance for the given parameters. Whereas with PLP-MC, the simulation results slightly improve as predicted in information theoretic results in Ref. [4]. With the proposed approach, the performance is significantly better than the other approaches. In particular, we notice a performance improvement of nearly 0.2 dB at σ△=2° and 0.1 dB at σ△=4°.
In Figure 3(b), the BER is shown as a function of γb with different phase noise variances σ△ for 64-QAM modulation with MLC scheme. As higher order modulations are more prone to phase noise which can be seen in Figure 3(b), in all the considered scenarios for different values of phase noise variance σ△, the proposed approach performs significantly better. It can be noticed from the simulation that for increased values of σ△, the performance of the proposed receiver is significantly better. The improvement in the performance of the receiver provides a significance of the effectiveness of the proposed approach at the expense of slight increase in processing overhead.
6 Conclusions
In this paper, we have investigated the performance of phase noise estimation algorithm in the presence of multiple samples available at the channel and receiver. An iterative receiver was designed, which inherently takes care of the ISI introduces due to the presence of multiple samples and performs phase synchronization. The proposed solution is particularly attractive from implementation point of view as it uses off- the-shelf block for detection and demodulation and can easily be extended to other demodulation and detection schemes. It was shown that the proposed scheme works significantly better than the commonly used well-known approaches. The proposed receiver structure confirms information theoretic studies and provides a low-complexity solution for implementing multi-sample receiver with robust performance at the expense of an increase in the processing overhead.
Contributors
All the authors equally contributed in this manuscript. In particular, MUHAMMAD Asim conceptualized the idea and derived the algorithms. ASFANDYAR Khan and JAVED Iqbal Bangash performed analysis of the proposed algorithms and finalized the receiver structure. Performance evaluation of the receiver structure was performed by the ABDULLAH Khan. Initial draft of the manuscript was written by MUHAMMAD Asim. All authors replied to reviewers’ comments and revised the final version. They appreciated anonymous reviewer’s for their constructive comments in improving the quality of this manuscript.
Conflict of interest
Authors of this manuscript declare that they have no conflict of interest.
References
[1] RUTMAN J, WALLS F. Characterization of frequency stability in precision frequency sources [J]. IEEE Proceedings, 1991, 79(7): 952-960. DOI: 10.1109/5.84972.
[2] MARTALO M, FERRARI G, ASIM M, GAMBINI J, MAZZUCCO C, CANNALIRE G, BIANCHI S, RAHELI R. Reduced-complexity synchronization for high-order coded modulations [C]// Proceedings of IEEE International Conference on Communication (ICC). London, UK, 2015: 4721-4726. DOI: 10.1109/ICC.2015.7249069.
[3] BARBIERI A, COLAVOLPE G. On the information rate and repeat accumulate code design for phase noise channels [J]. IEEE Transactions of Communication, 2011, 59(12): 3223-3228. DOI: 10.1109/TCOMM.2011.082011.100217.
[4] GHOZLAN H, KRAMER G. Multi-sample receivers increase information rates for Wiener phase noise channels [C]// Proc IEEE Global Telecommunication Conf (GLOBECOM). Atlanta, GA, 2013: 1897-1902. DOI: 10.1109/GLOCOM.2013.6831351.
[5] BARBIERI A, COLAVOLPE G, CAIRE G. Joint iterative detection and decoding in the presence of phase noise and frequency offset [J]. IEEE Transactions of Communication, 2007, 55(1): 171-179. DOI: 10.1109/TCOMM.2006.887501.
[6] VILA` VALLS L R J, BROSSIER J M. Joint oversampled carrier and time-delay synchronization in digital communications with large excess bandwidth [J]. Signal Processing, 2012, 92(1): 76-88. DOI: https://doi.org/10. 1016/j.sigpro.2011.06.008.
[7] SEPTIER F, DELIGNON Y, MENHAJ-RIVENQ A, GARNIER C. Particle filter with hybrid importance function for joint symbol detection and phase tracking [C]// IEEE 7th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC ’06). Cannes, France, 2006: 1-5. DOI: 10.1109/SPAWC. 2006.346358.
[8] SHEN Z, YU H, HU Y, SHEN C. Joint symbol detection for multireceiver without signal synchronization and array alignment [J]. IEEE Communication Letter, 2014, 18(10): 1755-1758. DOI: 10.1109/LCOMM.2014.2352644.
[9] FERTONANI D, BARBIERI A, COLAVOLPE G. Reduced-complexity BCJR algorithm for turbo equalization [J]. IEEE Transactions of Communication, 2007, 55(12): 2279-2287. DOI: 10.1109/TCOMM.2007.910638.
[10] ZHANG Lei, SHANG Yong, CHENG Yu-xin, XIANG Hai-ge. Improved turbo equalization base on soft ISI cancellation [J]. Signal Processing, 2009, 89(9): 1812-1820. DOI: https://doi.org/10.1016/j.sigpro.2009.03.019.
[11] NESHAASTEGARAN P, BANIHASHEMI A H. Log- likelihood ratio calculation for pilot symbol assisted coded modulation schemes with residual phase noise [J]. IEEE Transactions on Communications, 2019, 67(5): 3782-3790. DOI: 10.1109/TCOMM.2019.2896190.
[12] KREIMER A, RAPHAELI D. Efficient low-complexity phase noise resistant iterative joint phase estimation and decoding algorithm [J]. IEEE Transactions on Communications, 2018, 66(9): 4199-4210. DOI: 10.1109/ TCOMM.2018.2829865.
[13] ALFREDSSON A F, AGRELL E, WYMEERSCH H. Iterative detection and phase-noise compensation for coded multichannel optical transmission [J].IEEE Transactions on Communications, 2019, 67(8): 5532-5543. DOI: 10.1109/ TCOMM.2019.2912569.
[14] MEYR H, OERDER M, POLYDOROS A. On sampling rate, analog prefiltering, and sufficient statistics for digital receivers [J]. IEEE Transactions of Communication, 1994, 42(12): 3208-3214. DOI: 10.1109/26.339842.
[15] FORNEY G, GALLAGER R, LANG G, LONGSTAFF F, QURESHI S. Efficient modulation for band-limited channels [J]. IEEE Journal on Selected Areas in Communications, 1984, 2(5): 632-647. DOI: 10.1109/JSAC.1984.1146101.
[16] CASTOLDI P, RAHELI R. On recursive optimal detection of linear modulations in the presence of random fading [J]. European Transactions on Telecommunications, 1998, 9(2): 209-220. DOI: https://doi.org/10.1002/ett.4460090211.
[17] UNGERBOECK G. Channel coding with multilevel/phase signals [J]. IEEE Transactions on Information Theory, 1982, 28(1): 55-67. DOI: 10.1109/TIT.1982.1056454.
[18] LI Y, RYAN W E. Bit-reliability mapping in LDPC-coded modulation systems [J]. IEEE Communications Letters, 2005, 9(1): 1-3. DOI: 10.1109/LCOMM.200501010.
(Edited by YANG Hua)
中文导读
下一代无线通信系统的信道感知接收器
摘要:本文考虑一种基于最大后验概率算法的迭代相位同步方案。在经典方法中,相位噪声估计模型在信道和接收器的每个符号处考虑一个样本。但是,信息理论研究建议在信道和接收器的每个符号上使用多个样本以实现更高的性能。在本文中,得出了一种软信息辅助迭代接收器,该接收器使用现成的块进行检测和解调,以保持接收器的复杂性可接受。在这里,我们以务实的范例考虑每个符号在信道和接收器处的两个样本。结果表明,以适度的处理开销为代价,可以显著改善相位噪声估计。给出了针对低密度奇偶校验编码的正交幅度调制的仿真结果。结果表明,与传统的接收器方法相比,强相位噪声值具有显著的性能改善。
关键词:相位噪声通道;迭代接收器;多样本;LDPC编码调制
Received date: 2020-07-02; Accepted date: 2020-10-11
Corresponding author: MUHAMMAD Asim, PhD, Assistant Professor; Tel: +92-336-9147335; E-mail: muhammad.asim@aup.edu.pk; ORCID: https://orcid.org/0000-0003-3698-6126