Trans. Nonferrous Met. Soc. China 27(2017) 2512-2520

Relationship between alumina mixing characteristics and feeder configurations in aluminum reduction cells

Hong-liang ZHANG^1,2, Shuai YANG^1,2, Jie LI^1,2

1. School of Metallurgy and Environment, Central South University, Changsha 410083, China;

2. National Engineering Laboratory for High Efficiency Recovery of Refractory Nonferrous Metals, Central South University, Changsha 410083, China

Received 20 June 2016; accepted 9 October 2016

Abstract: Because of the increasingly prominent problem of alumina content inhomogeneity in large or super-scale aluminum reduction cells, a transient numerical model for the alumina mixing process was developed for a 400 kA cell, and the relationship between the alumina content distribution and electrolyte flow field was analyzed. In the ANSYS software platform, several numerical simulation cases were presented to display the influence of the feeder configuration on the alumina mixing characteristics. The results showed that a large vortex flow of the molten electrolyte is beneficial for alumina mixing and uniform distribution in the inner areas of the vortexes. The alumina particles reach the inter-electrode zone in 10-15 s from the beginning of the feeding action, and the risk of early precipitation occurs in 10-25 s after the feeding. It was also found that a suitable grouping of feeders could reduce the content fluctuation and gradient. Therefore, a feeding on demand strategy was proposed, and the simulation results showed that although the spatial characteristics are not changed, the uniformity of the alumina content was markedly improved.

Key words: aluminum electrolysis; content distribution; feeder configuration; alumina precipitation

1 Introduction

Alumina is one of the most important raw materials in the aluminum electrolysis industry. Its uniform distribution inside a molten electrolyte is conducive to a more stable magnetohydrodynamic (MHD) equilibrium, fewer pollutant emissions and a longer cell life. Otherwise, the distribution will seriously affect production. For example, if the alumina concentration is too high, alumina precipitation will occur, which can significantly reduce the current efficiency. However, if the concentration is too low, the anode effect (AE) will occur, which will dramatically increase the energy consumption and pollute emissions. Therefore, the alumina concentration distribution has become a key factor in achieving better economic and technological indexes in modern large-scale aluminum reduction cells in China [1].

Because of the high temperature, corrosive conditions of the electrolyte and the complex mixing and dissolution behavior of alumina, studies on the alumina concentration in industrial cells are extremely difficult, and computational fluid dynamics (CFD) is the only effective research approach. Many studies have been conducted in the past few years. PONCSAK et al [2] performed studies in a simulation cell, and the results showed that the alumina mixing time was shortened when the feeder was positioned in the cross area between the center channel and the gap between the anodes. FENG et al [3,4] studied the transport of alumina with CFD, and the alumina feeding and consumption were considered using a multicomponent model. Similar studies were also carried out by ZHAN et al [6-9]. ZHANG et al [10,11] analyzed the alumina concentration distribution using a vortex structure method. The above studies mainly focused on the modeling method and alumina transport mechanism, and location optimization was performed in some studies.

However, very few studies have been conducted on the relationship between the alumina concentration and the feeder configuration, especially for large scale cells that are over 400 kA. These studies are important for theoretical research and practice. As the cell size increases, the uniformity of the alumina concentration becomes a problem in many industrial cells. This can lead to failure of the control system, fluctuation in the cell status and high energy consumption.

Therefore, a transient numerical model for the alumina mixing process was developed based on the characteristics of a feeder system in the present 400 kA industrial cells, and the relationship between the alumina concentration distribution and electrolyte flow field was analyzed. Several application cases were calculated to study the influences of the feeder configuration, which mainly included the feeding sequence and feeder size, on alumina mixing behaviors.

2 Mathematic model

2.1 Electrolyte-gas two phase flow and alumina multicomponent model

The melt flow is governed by the laws of mass conservation, momentum conservation and energy conservation, which can be described by the Navier- Stokes equations:

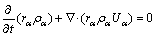                    (1)

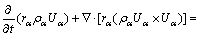
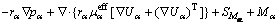     (2)

where r_α, ρ_α, 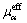, p_α and U_α represent the volume fraction, density, effective viscosity, pressure and velocity of the α phase, respectively; M_α is the interphase surface force; and S_Mα is the external force.

The external force are mainly the gravity force, buoyancy, Lorenz force F_EM, and interphase force, which is the drag force between the electrolyte phase and the bubble phase. These forces can be calculated using the following equations:

S_Mb=r_bF_EM                                      (3)

M_be=C_b,p(U_p-U_b)                              (4)

S_Mp=r_p(ρ_b-ρ_p)g                               (5)

where C_b,p is the friction coefficient between the electrolyte and the bubble phase, as shown in the following equation:

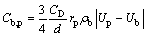                     (6)

where C_D is the drag coefficient, which can be calculated using the Ishii-Zuber equations. The Lorenz force F_EM, can be calculated using the following equation:

F_EM=J×B                                    (7)

where J is the current density, and B is the magnetic flux density.

In an aluminum reduction cell, the above Navier- Stokes equations can be solved using a homogeneous standard k-ε turbulence model.

The conservation component is also needed for the molten electrolyte with the dissolved alumina:

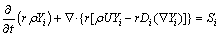          (8)

where r, r and U represent the volume fraction, density and velocity of the electrolyte phase, respectively; Y_i, D_i and S_i represent the mass fraction, diffusion coefficient and mass source terms of component i in the electrolyte, respectively [12].

2.2 Alumina feeding and consumption

1) Alumina consumption

Because of the inhomogeneous distribution of the current density, there are large differences in the alumina consumption rate. The consumption can be calculated using the following equation:

m_loc=1.76J_bη                                 (9)

where m_loc is the local consumption rate, J_b is the current density distribution of the bottom surface of the electrolyte layer, and η is the current efficiency.

2) Alumina feeding

The amount of alumina feeding was determined by the feeder size, and the amounts were mainly 1.2, 1.6, 1.8, 2.0 kg, etc. During the industrial alumina feeding control model, the feeding rate is controlled through a feeding interval. After the feeding operation, the alumina powder is gradually dissolved in the electrolyte via the flow field. Therefore, on the basis of the alumina behavior, the alumina travel time variable in the process could be transformed into an angular function. The feeding rate can be calculated using the following equation:

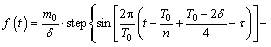
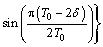                       (10)

where m₀ is the feeder size; δ is the time required for the dissolution of alumina, which is 10 s according to the previous work [13]; T₀ is the feeding time interval; n is the group of feeders; τ is the time delay for the dissolution of alumina, which is 5 s in this work; and t is the time variable.

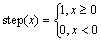                           (11)

2.3 Transient model calculation and case introduction

A transient numerical model for the alumina mixing process was developed in the ANSYS software platform, and the relationship between the alumina concentration distribution and the electrolyte flow field was studied in a 400 kA cell. The main structure and parameters are displayed in Table 1, where ACD is the anode cathode distance. There are six uniformly laid out feeders in the upper structure, which are labeled FD1 to FD6, respectively, as shown in Fig. 1. The anodes are labeled A1 to A24 and B1 to B24, as shown in Fig. 1. The coordinates of the observation points OB1 to OB12 are listed in Table 2. The boundary conditions of the multicomponent model are listed in Table 3 [14,15].

Procedure for calculations:

1) The electric and magnetic fields were calculated using previously developed finite element models (FEM). Based on these results, the Lorenz force and alumina consumption rate were calculated. The calculation mesh for the multicomponent model is shown in Fig. 2.

2) The electrolyte-bubble two phase steady flow field was then calculated using a homogeneous alumina content of 2.5%. The alumina contents discussed in the following are all given as a mass fraction.

3) By adopting the alumina feeding and consumption functions, the transient multicomponent multiphase model for the alumina concentration distribution was calculated with a feeder size of 1.6 kg and a feeding time interval of 136 s.

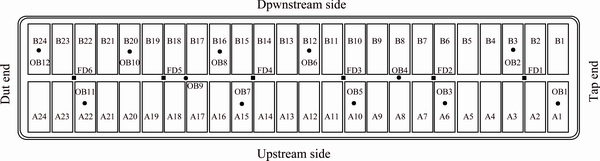
Fig. 1 Distribution of feeders and set observation points

Table 1 Main structure and parameters of studied 400 kA cell

Table 2 Coordinates of set observation points OB1 to OB12

Table 3 Boundary conditions of multicomponent model

2.4 Results

In previously published works, a number of analysis methods were used to determine the alumina content, such as the average mean value of content, maximum value of content, minimum value of content, regional area of content and other target variables [3,16]. However, to evaluate the content distribution characteristics, the cell was divided into 6 regions labeled 1-6 from the tape end to the duct end in this work. In each region, the distribution characteristics, combined standard deviation and other traditional analysis methods for concentration were discussed. The standard deviation was calculated using

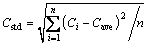                    (12)

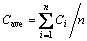                             (13)

where C_i is the content for each discrete element in the calculation domain; C_ave is the mean of alumina content in each region; and n is the number of the discrete element.

Furthermore, because of the limited abilities of the standard deviation to describe the characteristic regions, a method for judging and evaluating the concentration area was proposed. This method will be used to count the area of the alumina content distribution in each region.

3 Relationship between alumina content and electrolyte flow field

The steady state flow field distribution of a 400 kA cell is presented in Fig. 3, and the location of the feeders and the direction of the flow are also marked. Figures 4 and 5 show the inter-polar concentration distributions of feeder 6 after one feeding cycle and after 1360 s, respectively, in plane z=1.132 m (the z axis is the vertical direction of the cell, as shown in Fig. 2, and z=1.132 m is the middle layer between the anode and the cathode).

Figure 3 shows that there are two large vortexes, and the one near the duct end is smaller. The feeders are in different regions of the vortexes. FD4 and FD6 are located in the area of the fast velocity of the vortex edge, FD1 and FD3 are located in the vortex internal edge with a relatively low velocity, and FD2 and FD5 are located in the center of vortex with a very low velocity. Figure 4 indicates that the direction of the alumina mixing is along the flow direction. Figures 4(b), (d) and (e) show that the alumina from FD1 and FD6 is transported to side A, the alumina from FD3 and FD4 is transported to side B, and the alumina from FD2 and FD5 is limited to a small region around the feeder location.

Figures 3 and 5 show that the uniformity of the concentration in the vortex edge is better than that in the vortex center. As the alumina from FD4 and FD6 feeders was transported a longer distance in a larger region, the alumina content distribution is more uniform than in the FD2 and FD5 feeders. A similar phenomenon was found in the FD1 and FD3 feeders. Therefore, the content near the FD1 and FD3 feeders is larger because of the weaker dispersion.

Fig. 2 Mesh for multicomponent model

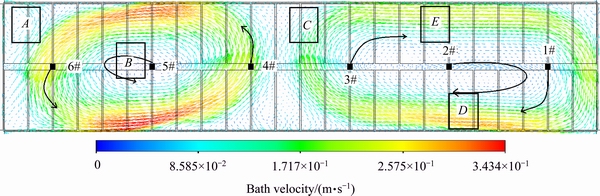
Fig. 3 Steady state flow field of 400 kA cell

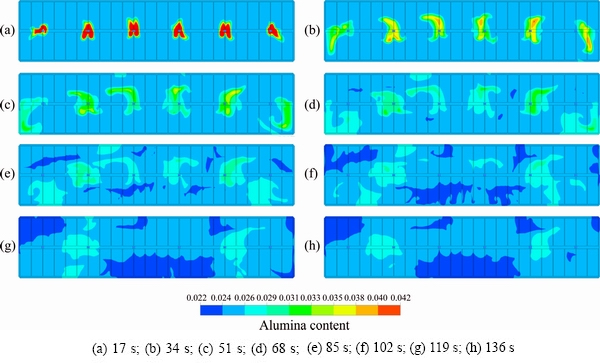
Fig. 4 Inter-polar concentration distribution of feeder 6 after one feeding cycle (z=1.132 m)

Fig. 5 Inter-polar concentration distribution of feeder 6 after 1360 s (z=1.132 m)

The alumina content is very low in region A of   Fig. 5. The reason is that it is difficult to transport alumina to this area because it is located at the external outside of the vortex, and the flow rate or the velocity will not affect the content in region A. A similar phenomenon can also be found in region C, whereas the concentration is higher in region D. The reason for this may be that region D is located in the cross transport direction of the FD1 and FD2 feeders, and alumina from both feeders can therefore be transported to region D.

Generally, the electrolyte flow field is the direct factor for alumina transport, especially for a large vortex. A more uniform concentration distribution will be achieved if the feeder is located at the edge of the vortex with a faster transport speed. However, if the feeder is located at the vortex center, there will be difficulties in transporting the alumina because of the very low  velocity. The consequence is that alumina precipitation occurs in this location. Moreover, the content will be very low in the region located outside of the vortex because of the slow alumina transport.

4 Relationship between alumina content and feeder configuration

4.1 Synchronous feeding

Synchronous feeding means that all the feeders feed at the same time with the same amount of alumina. For example, if the feeder size is 1.6 kg, then the total feeding amount will be 9.6 kg. Generally, the time interval for each feeding is 136 s. The contour distribution in the plane z=1.132 m after each feeding cycle is shown in Fig. 6. The mean values of the content, standard deviation and range of content are listed in Table 4.

Figure 6 indicates that there are large differences in the content distribution in the horizontal plane. Although the patterns are similar for each feeding cycle, the content is different for the first six cycles. After that, there is very little difference in the content, which can be regarded as a steady state. In region A to D, the largest challenge is the inadequate supply of alumina, which could lead to anode effect. However, in regions E and F, too much alumina is a problem, which will cause alumina precipitation.

In Table 4, the overall distribution range is from 2.227% to 3.05% with a deviation of 0.823%. This is a large deviation range, and the control accuracy of the concentration is below 1%. There is a similar deviation in every region, and negative deviations appeared in regions 3, 4 and 6 and positive deviations appeared in regions 1, 2 and 5. Moreover, the deviations in region 2, 5 and 6 are about two times greater than those in the other three regions.

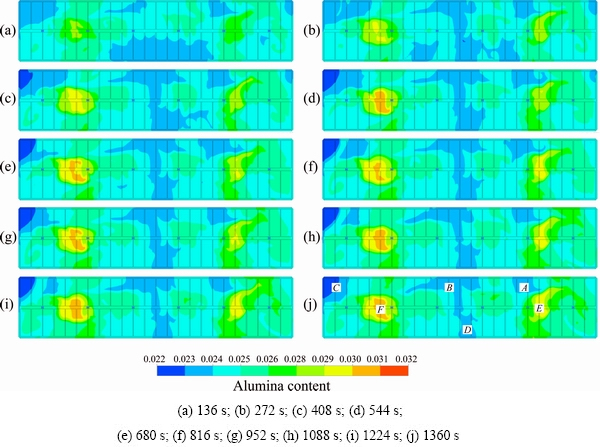
Fig. 6 Contour of alumina content distribution in plane z=1.132 m after each feeding cycle

Table 4 Average value, standard deviation and range of content

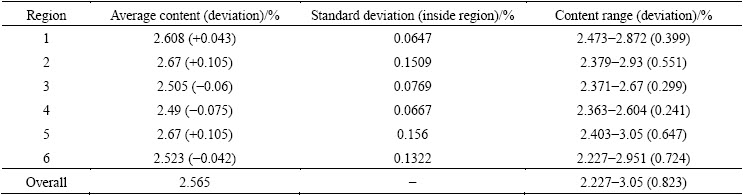
The time varying characteristic of the alumina content in the plane z=1.132 m in OB1 to OB12 is shown in Fig. 7, and the time varying characteristics for the area of high content (>2.8%) and low content (<2.3%) are shown in Fig. 8.

There is a clear distinction in the time varying characteristics for each observation point, where, except for OB12, the other 11 points appear to have a similar pattern with a different fluctuation range. Based on the range in Fig. 7(b), the characteristics are completely inconsistent for OB10 and OB12 compared with the others. This means that the alumina mixing characteristics are very complicated in both the space and time domain.

Figure 8 shows that the time varying characteristic for the area of high content is consistent with the feeding cycle. The high content peak area value can reach 12 m² and is gradually reduced to 4 m² after each feeding cycle. This indicates that there are large spatial differences even within one feeding cycle. However, the area of low content is relatively stable and is roughly ~1 m².

Figure 9 shows the content distribution in the vertical (z axis) section of the FD1 and FD2 feeders after feeding for 50 s. It can be seen that the transportation speed in the vertical direction is very fast after feeding. For approximately 10 s, alumina can reach the interface and transport horizontally, which agrees with the previous observation in the industrial cell [17]. Within 10-20 s, the vertical transportation will be finished, and the inter-electrode alumina content will remain stable. Therefore, from the perspective of vertical transportation of alumina, the greatest risk of alumina precipitation is between 10 and 25 s.

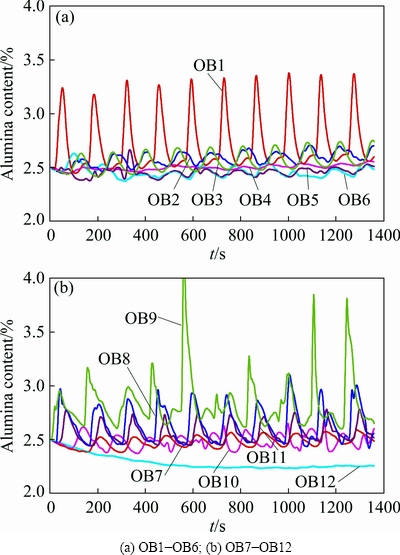
Fig. 7 Time varying characteristics of alumina content in plane z=1.132 m

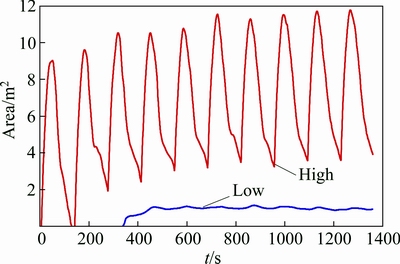
Fig. 8 Time varying characteristics for areas of high content (>2.8%) and low content (<2.3%) in plane z=1.132 m

4.2 Asynchronous feeding

Asynchronous feeding has been applied in some large aluminum reduction cells. All the feeders are divided into several groups, and the groups are fed by sequence. In this case, FD1, FD3 and FD5 feeders are defined as group 1, and the other three are defined as group 2. The feeding time interval for each group is 68 s, and the feeder size is still 1.6 kg. The alumina content for the asynchronous feeding in the plane z=1.132 m at  1292 s and 1360 s are shown in Fig. 10.

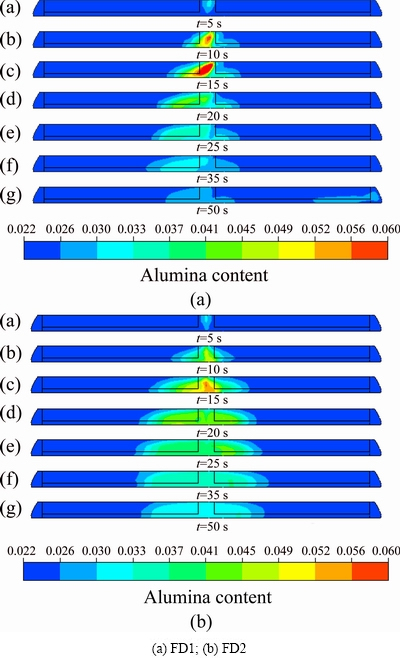
Fig. 9 Content distribution in vertical (z axis) section of feeders after feeding for 50 s

Although the distributions of the high content and low content areas are mostly consistent for the two feeding configurations, the values are slightly different. The reason is that the electrolyte flow field determines the content distribution. For the optimal content distribution, the feeding strategy for each should be different, which is called as feeding on demand.

4.3 Feeding on demand

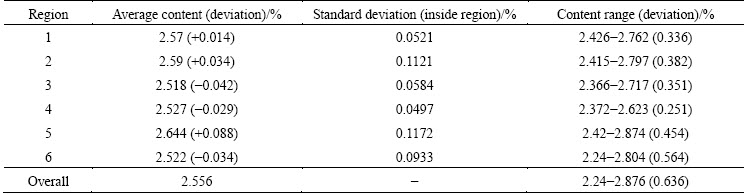
On the basis of the above studies, a feeding on demand strategy was proposed. The original symmetric feeding configuration (6 × 1.6 kg) was modified. The FD1, FD3, FD4 and FD6 feeder sizes were increased to 1.8 kg, and the FD2 and FD5 feeder sizes were reduced to 1.2 kg. The feeding time interval was still 136 s, and the total feeding amount each time was unchanged. The contour of the alumina content distribution for the feeding on demand strategy in plane z=1.132 m is shown in Fig. 11. The average values, standard deviation and range for the content in feeding on demand are listed in Table 5.

From Fig. 11, it can be observed that the spatial characteristics are unchanged, but the alumina contents in FD2 and FD5 are much higher. This means that the slight change in the feeder size does not have a fundamental impact on the concentration distribution. Table 5 and Table 4 show that the uniformity was improved in this case, and the standard deviation and the content fluctuation range were reduced. The feeding on demand strategy is beneficial for the uniform distribution of the alumina content.

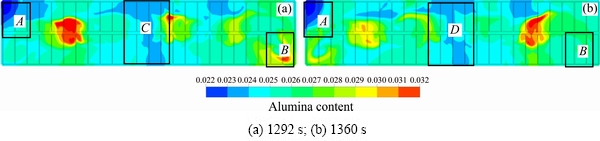
Fig. 10 Contour of alumina content distribution for asynchronous feeding strategy in plane z=1.132 m

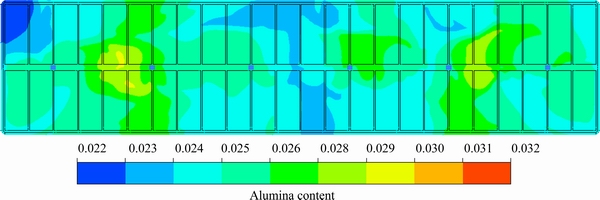
Fig. 11 Contour of alumina content distribution for feeding on demand strategy in plane z=1.132 m (t=1360 s)

Table 5 Average value, standard deviation and range of content for feeding on demand (t=1360 s)

Theoretically, feeding on demand can optimize the uniformity, but it has some defects, such as poor adjustability because of the current design of the upper system in a reduction cell, which cannot be modified once it is built. Moreover, it is neither economical nor applicable for single point feeding because of the complex electrical and mechanical structures in cell upper systems, which will lead to control failure in the regional concentration compensation or regional anode effect extinction. This is why feeding on demand should be continually studied theoretically and practically, especially in design and industrial experiments.

5 Conclusions

1) The most direct impact factor on the mixing of alumina is the flow field of the electrolyte. A large vortex flow is beneficial to alumina mixing, and a uniform content distribution can be achieved at the edge of the large vortexes. However, the alumina content can reach a high level with a large gradient because of the poor mixing ability at the center of the vortexes.

2) Alumina reaches the inter-electrode zone in 10-15 s from the beginning of the feeding action, and the risk of early precipitation is 10-25 s after feeding. The maximum alumina content can reach 5% near the metal-electrolyte interface at the end of the feeding cycle.

3) A suitable group of feeders and an asynchronous feeding strategy could reduce the content fluctuation and content gradient in the electrolyte, which is beneficial for overall uniformity. Although the distribution areas for the high and low contents are basically consistent for the two feeding configurations, the values are slightly different.

4) A feeding on demand strategy was proposed, and the simulation results showed that although the spatial characteristics are unchanged, the uniformity of the alumina content can be improved.

References

[1] LIU Ye-xiang, LI Jie. Modern aluminum electrolysis [M]. Beijing: Metallurgical Industry Press, 2008: 35-85. (in Chinese)

[2] PONCSAK S, KISS L, TOULOUSE D, PERRON A, PERRON S. Size distribution of the bubbles in the Hall-Héroult cells [C]// GALLOWAY T J. Light Metals 2006. San Antonio, TX: TMS, 2006: 457-462.

[3] FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells [C]//HAGNI A M. Light Metals 2010. Seattle, WA: TMS, 2010: 451-456.

[4] FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells [C]//LINDSAY J. Light Metals 2011. San Diego, CA: TMS, 2011: 543-548.

[5] VON K R, ANTILLE J, ROMERIO M, BESSON O. Impact of magnetohydrodynamic and bubbles driving forces on the alumina concentration in the electrolyte of an HallHéroult cell [C]//SADLER B. Light Metals 2013. San Antonio, TE: TMS, 2013: 585-590.

[6] ZHAN Shui qing, LI Mao, ZHOU Jie min, ZHOU Yi wen, YANG Jian hong. Numerical simulation of alumina concentration distribution in melts of aluminum reduction cells [J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2658-2667. (in Chinese)

[7] ZHAN Shui-qing, LI Mao, ZHOU Jie-min, YANG Jian hong, ZHOU Yi wen. CFD simulation of dissolution process of alumina in an aluminum reduction cell with two-particle phase population balance model [J]. Applied Thermal Engineering, 2014, 73(1): 803-816.

[8] ZHAN Shui-qing, LI Mao, ZHOU Jie-min, YANG Jian hong, ZHOU Yi wen. Analysis and modeling of alumina dissolution based on heat and mass transfer [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(5): 1648-1656.

[9] ZHAN Shui-qing, LI Mao, ZHOU Jie-min, YANG Jian hong, ZHOU Yi wen. CFD simulation of effect of anode configuration on gas-liquid flow and alumina transport process in an aluminum reduction cell [J]. Journal of Central South University, 2015, 22(7): 2482-2492.

[10] ZHANG He-hui. Numerical study of vortex flow of melts and transport process of alumina in aluminum reduction cells [D]. Changsha: Central South University, 2012. (in Chinese)

[11] LI Jie, ZHANG He-hui, ZHANG Hong-liang, XU Yu-jie, YANG Shuai, LAI Yan-qing. Numerical simulation on vortical structures of electrolyte flow field in large aluminium reduction cells [J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 2082-2089. (in Chinese)

[12] WONG D S, TABEREAUX A, LAVOIE P. Anode effect phenomena during conventional AEs, low voltage propagating AEs & non-propagating AEs [C]//GRANDFIELD J. Light Metals 2014. San Diego, CA: TMS, 2014: 529-534.

[13] LILLEBUEN B, BUGGE M, HOIE H. Alumina dissolution and current efficiency in Hall-Héroult cells [C]//BEARNE G. Light Metals 2009. San Francisco, CA: TMS, 2009: 389-394.

[14] SOLHEIM A. The density of molten NaF-LiF-AlF₃-CaF₂-Al₂O₃ in aluminium electrolysis [J]. Aluminum Transactions, 2000, 2(1): 162-168.

[15] TAYLOR M P, ZHANG W D, WILLS V, SCHMID S. A dynamic model for the energy balance of an electrolysis cell [J]. Trasactions of the Institution of Chemical Engineers, 1996, 74(8): 913-933.

[16] ZHANG Hong-liang, YANG Shuai, ZHANG He-hui, LI Jie, XU Yu-jie. Numerical simulation of alumina-mixing process with a multicomponent flow model coupled with electromagnetic forces in aluminum reduction cells [J]. JOM, 2014, 66(7): 1210-1217.

[17] MAJID N A A, TAYLOR M P, CHEN J J J, STAM M A, MULDER A YOUNG B R. Aluminium process fault detection by multiway principal component analysis [J]. Control Engineering Practice, 2011, 19(4): 367-379.

铝电解槽氧化铝输运特性与下料配置的关系

张红亮^1,2，杨 帅^1,2，李 劼^1,2

1. 中南大学 冶金与环境学院，长沙 410083；

2. 中南大学 难冶有色金属资源高效利用国家工程实验室，长沙 410083

摘  要：针对特大型铝电解槽内氧化铝含量不均匀性日益突出的问题，建立了铝电解槽内氧化铝输运过程的瞬态数学模型。以某400 kA铝电解槽为实例，计算分析了槽内氧化铝含量分布与电解质流动、下料系统配置的关系。结果表明，电解质的大漩涡流动有利于氧化铝在漩涡内快速输运，实现漩涡内部浓度均匀分布；氧化铝下料后10~15 s即可输运到极间，早期沉淀风险发生在下料后的10~25 s；分组交叉的下料配置可减少槽内含量波动，并一定程度上改善了含量分布的均匀性。在此基础上，提出了铝电解槽“分区按需下料”策略，尽管含量的空间分布特性未发生根本性改变，但全槽氧化铝含量分布的均匀性得到了明显的优化。

关键词：铝电解；含量分布；下料配置；氧化铝沉淀

(Edited by Xiang-qun LI)

Foundation item: Projects (51574289, 61533020, 51674300) supported by the National Natural Science Foundation of China; Project (2015CXS017) supported by Innovation-driven Plan in Central South University, China

Corresponding author: Hong-liang ZHANG; Tel: +86-13574831278; E-mail: csu13574831278@csu.edu.cn

DOI: 10.1016/S1003-6326(17)60278-4