大口径薄壁Ti-6Al-4V管材数控温弯中不同应变速率和温度下的Johnson-Cook本构模型
来源期刊:中国有色金属学报(英文版)2018年第2期
论文作者:陶智君 樊晓光 杨合 马俊 李恒
文章页码:298 - 308
关键词:数控温弯;Ti-6Al-4V管;Johnson-Cook本构模型
Key words:NC warm bending; Ti-6Al-4V tube; Johnson-Cook model
摘 要:大口径薄壁Ti-6Al-4V管是航空航天等高端制造领域亟需的典型轻量化高性能构件,数控温弯能够有效实现大口径Ti-6Al-4V管的精确成形。由于数控温弯工艺过程是多场耦合复杂变形过程,建立其材料本构模型并实现全过程有限元模拟是亟待解决的瓶颈技术。利用管材单向拉伸实验,结合温弯工艺参数变化,研究温度在25~600 °C和应变速率在0.00067~0.1 s-1情况下Ti-6Al-4V管的力学性能。考虑非线性硬化率和应变的交互作用,建立了修正的Johnson-Cook本构模型,并根据实验数据对相关修正参数进行了拟合。将该模型应用于温弯模拟中可发现,修正的JC模型与传统的模型相比,可降低最大误差90%,并且可以有效预测管材断裂、起皱等成形缺陷发生的位置,为大口径薄壁Ti-6Al-4V管数控温弯成形极限和工艺优化奠定基础。
Abstract: Numerical control (NC) warm bending is a proven strategy to form the large diameter thin-walled (LDTW) Ti-6Al-4V tubes, which are typical light-weight and high-performance structural components urgently required in many industries. In virtue of unveiling the thermo-mechanical coupled deformation behaviors, uniaxial tensile tests were conducted on Ti-6Al-4V tube within wide ranges of temperatures (25-600 °C) and strain rates (0.00067-0.1 s-1). Moreover, a modified Johnson-Cook (JC) model is proposed with a consideration of nonlinear strain rate hardening and the interaction between strain hardening and thermal softening. Resultantly, the present model gives more accurate predictions for flow stress over the entire deformation ranges and the maximum error decreases by about 90%. By employing proposed model to NC warm bending, preferable precision is obtained in predicting forming defects including fracture, wrinkling and over thinning. The present work lays foundation for the forming limit prediction and process optimization in NC warm bending of LDTW Ti-6Al-4V tubes.
Trans. Nonferrous Met. Soc. China 28(2018) 298-308
Zhi-jun TAO, Xiao-guang FAN, He YANG, Jun MA, Heng LI
State Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received 20 September 2016; accepted 24 March 2017
Abstract: Numerical control (NC) warm bending is a proven strategy to form the large diameter thin-walled (LDTW) Ti-6Al-4V tubes, which are typical light-weight and high-performance structural components urgently required in many industries. In virtue of unveiling the thermo-mechanical coupled deformation behaviors, uniaxial tensile tests were conducted on Ti-6Al-4V tube within wide ranges of temperatures (25-600 °C) and strain rates (0.00067-0.1 s-1). Moreover, a modified Johnson-Cook (JC) model is proposed with a consideration of nonlinear strain rate hardening and the interaction between strain hardening and thermal softening. Resultantly, the present model gives more accurate predictions for flow stress over the entire deformation ranges and the maximum error decreases by about 90%. By employing proposed model to NC warm bending, preferable precision is obtained in predicting forming defects including fracture, wrinkling and over thinning. The present work lays foundation for the forming limit prediction and process optimization in NC warm bending of LDTW Ti-6Al-4V tubes.
Key words: NC warm bending; Ti-6Al-4V tube; Johnson-Cook model
1 Introduction
Titanium alloys have been extensively used in aerospace, defense, energy and medical industries [1]. Tubes made from them, especially large diameter thin-walled (LDTW) Ti-6Al-4V tubes, satisfy the requirements of weight reduction, energy economization, high-pressure resistance, and gain increasing applications in hydraulic pneumatic, fuel or environment control systems for advanced aircraft and spacecraft [2].
Rotary draw bending (RDB) is advantageous in achieving stable bending and thus becomes an ideal forming technology for manufacturing LDTW titanium tubes [3]. However, the formability of Ti-6Al-4V tube is limited at room temperature, viz. cracking and tearing occurring during room-temperature bending [4]. Furthermore, under multi-die constraints as shown in Fig. 1, RDB is a tri-nonlinear physical process which is affected by various parameters. Many potential defects such as wrinkling, over thinning and cross-section distortion happen easily. Therefore, a new forming technology is urgently needed in the RDB of LDTW Ti-6Al-4V tube.
As reported by many investigators [5-10], increasing working temperature leads to the reduction of deformation resistance and the improvement of formability in many sheet metal forming processes, e.g. CP-Ti tubes warm bended at 300 °C [6,7], Ti-6242 sheets hot formed at 1050 °C (above the transition- temperature) [8] and TC4 sheets warm deep drawn at 400 °C [9]. According to LAI et al [8], the formability of TC4-tailored welded blanks (TWBs) can be enhanced by elevated tooling temperatures, and the optimum forming behavior of TC4-TWB is achievable under the nearly isothermal forming condition at (550±10) °C for both tooling and TWB specimen. Thus, it is believed to be a practical method to achieve bending of Ti-6Al-4V tube at suitable elevated temperature without inducing defects. An understanding of thermo-mechanical deformation behaviors of Ti-6Al-4V tube within wide ranges of temperature and strain rates is the prerequisite of reliable numerical simulation of above-mentioned warm rotary draw bending (WRDB) process and processing parameters optimization based on it, and is thus of great importance [11].
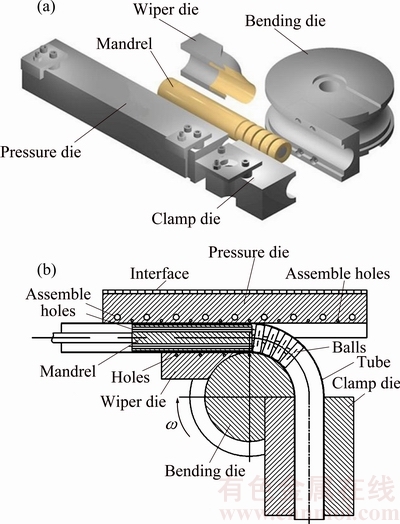
Fig. 1 Relative mounting position (a) and principle (b) of NC bending process [2]
To date, numerous efforts have been conducted to investigate the deformation behaviors and formability of titanium sheets and pillars at different strain rates and temperatures. LAI et al [12] proposed a set of isothermal uniaxial tests of Ti-6Al-4V using flat-sheet samples at temperatures ranging from room temperature up to 400 and 650 °C, respectively. Compared with room temperature condition, approximately half the ultimate tensile stress and twice the maximum strain are achieved at 650 °C. CHEN et al [13] studied the temperature dependent work hardening in Ti-6Al-4V alloy over large temperature ranges (20-900 °C) and strain rate ranges by the uniaxial compression tests. KOTKUNDE et al [14] also noticed the complicated interaction between strain hardening and thermal effects. Nevertheless, mechanical tests of Ti-6Al-4V based on curve-section samples at elevated temperatures are still less reported, resulting in limited comparability between mechanical tests and actual WRDB process. Additionally, an accurate prediction of flow behaviors of Ti-6Al-4V by considering the combined effects of strain, strain rate and temperature is essential for understanding flow responses in tube WRDB process.
In past decades, numerous phenomenological constitutive models, which unite high precision and simple implementation, have been developed in order to capture the coupling effects of deformation parameters. Among these models, the Fields-Bachofen model studied in Refs. [15-17] is a multiplication typed model with simple expression and is able to predict the thermal effect well. However, it is not suitable for predicting complex deformation process and thus satisfied prediction can only be achieved in a strain range of 0.1-0.3 and a temperature range of 150-300 °C for AZ31 alloy as indicated by CHENG et al [18] and LIN and CHEN [19]. Moreover, KOTKUNDE et al [20] also drew conclusion that Fields-Bachofen model was not suitable for prediction of flow behavior of Ti-6Al-4V alloy at elevated temperatures. The Johnson-Cook (JC) model [21] is another extensively used model which considers strain hardening, strain rate hardening/ softening and thermal softening separately by using multipliers. With certain modifications of the original JC model, many characteristic deformation behaviors become predictable including the nonlinearity of logarithmic strain rate dependence [22], complex thermal dependence [23] and flow localization induced softening [24]. And some modified forms of JC constitutive models and parameters calibration methods were also developed to achieve higher prediction accuracy [25-27]. KHAN and LIANG [28,29] established a series of half-phenomenological models comprising Khan-Huang-Liang model, Khan-Liang- Farrokh model [30], etc. With these models, the effects of temperature/ deformation history, grain size and also coupling effects between temperature and hardening behaviors are taken into consideration. Nevertheless, the complexity of model formulation and parameter optimization also multiplies.
With above-mentioned analyses in mind, isothermal uniaxial tensile tests of Ti-6Al-4V tube have been carried out using curve-section specimens in a temperature range of 25-600 °C and a strain rate range of 0.00067-0.1 s-1. Deformation behaviors of the alloy have been characterized via both microstructure observation and constitutive analyses. Finally, a modified JC model considering the coupling effects among strain, strain rate and temperature, was originally developed and verified within wide ranges of temperatures and strain rates.
2 Experimental
A commercial Ti-6Al-4V tube of 1 mm in wall thickness, with an average initial grain size of 10 μm (shown in Fig. 2), was used in this work. Quasi-static tensile tests were performed on a CMT5205 universal testing machine equipped with a heating furnace at temperatures ranging from 25 to 600 °C and strain rates of 0.00067-0.1 s-1. Three tests for every testing condition were carried out. The dimensions of specimens (GB/T 4338—2006) for tensile tests are shown in Fig. 3. The microstructures near the fracture zone of the deformed specimens were observed by means of scanning electron microscope (SEM) in order to compare the deformation behaviors of Ti-6Al-4V alloy at different strain rates and temperatures.

Fig. 2 Microstructure of as-received Ti-6Al-4V tube

Fig. 3 Test specimen and sampling schematic (unit: mm)
3 Experimental results
Figure 4 shows the flow curves at different temperatures and strain rates. It can be seen in Fig. 4(a) that with increasing testing temperature from 25 to 600 °C, the flow stress shows an obvious drop of about 50%. Moreover, increasing testing strain rate causes the evident increase of flow stress and the strain hardening rate, as observed in Fig. 4(b).
It is noteworthy that significant flow softening is observed with the increase of deformation temperature within the whole temperature range. However, fracture strain barely changes at 250-450 °C but exhibits remarkable increase at 500-600 °C. Overall, 500 °C can be approximately considered as the critical temperature for the warm/hot deformation of Ti-6Al-4V tube and also the threshold temperature of processing including machining and hot working [13].

Fig. 4 True stress-true strain curves of Ti-6Al-4V tube
The change of deformation behaviors is usually related with the variation of the microstructure evolution mechanisms. As a result, the microstructures of Ti-6Al-4V tube samples deformed at different temperatures and strain rates, as illustrated in Figs. 5 and 6, are further analyzed. When the temperature is lower than 500 °C, the microstructure of the specimen is characterized by light transformed β decorated around elongated coarse gray α. Within the scope of hot working, i.e., 500-600 °C, part of α phase transforms into β phase, and the increase of β phase at high temperatures leads to higher ductility and formability since β phase is relatively soft and is beneficial to the compatibility of deformation. Moreover, the change of volume fraction of β phase also leads to the variation of control mechanisms in hot deformation of titanium alloy, such as dynamic recovery, dynamic recrystallization, grain boundary sliding and adiabatic shear banding [31-34]. Especially at 600 °C and 0.00067 s-1, the elongation is significantly improved, as shown in Fig. 4(a); meanwhile, equiaxed and refined α grains are exhibited. The decrease of α grain size can be attributed to the recrystallization caused by the strain localization and the local adiabatic deformation heating [35]. Subsequently, the refined α grains bring about the change of deformation mechanism from dislocation gliding to grain boundary sliding, which can lead to the enhancement of plasticity.

Fig. 5 Microstructures of fracture zone of samples

Fig. 6 Microstructures of fracture zone of samples tested at different temperatures with strain rate of 0.00067 s-1
4 Constitutive modeling
In order to describe the constitutive response of the as-received Ti-6Al-4V tube, the flow stress (σ) in the Johnson-Cook (JC) model [21] is defined as a function of plastic strain (ε), strain rate (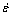 ) and temperature (T):
) and temperature (T):
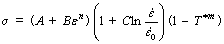 (1)
(1)
where 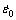 (0.00067 s-1 in this work) is the reference strain rate, T*=(T-Tr)/(Tm-Tr) (Tm is the melting temperature (1660 °C in this work) and the reference temperature Tr is determined as 25 °C in this work), A is the yield stress under the reference temperature and strain rate, B and n are strain hardening coefficient and exponential, respectively, C describes strain rate hardening and m accounts for thermal softening effects.
(0.00067 s-1 in this work) is the reference strain rate, T*=(T-Tr)/(Tm-Tr) (Tm is the melting temperature (1660 °C in this work) and the reference temperature Tr is determined as 25 °C in this work), A is the yield stress under the reference temperature and strain rate, B and n are strain hardening coefficient and exponential, respectively, C describes strain rate hardening and m accounts for thermal softening effects.
4.1 Procedure of data processing
The five constitutive parameters required by the JC model can be determined from experimental results using the following procedures:
1) Determination of A, B and n
At reference temperature and reference strain rate, Eq. (1) is reduced to
σ=A+Bεn (2)
By taking natural logarithm of Eq. (2), Eq. (3) is gained as follows:
ln(σ-A)=ln B+nln ε (3)
Then, ln(σ-A) is plotted against ln ε and thus B is obtained from the y-intercept and n from the slope.
2) Determination of C
At reference temperature, Eq. (1) can be expressed as
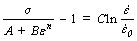 (4)
(4)
The flow stress at the same temperature and strain but different strain rates is used to plot [σ/(A+Bεn)-1] vs 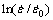 , and then C can be obtained from the slope of the curve.
, and then C can be obtained from the slope of the curve.
3) Determination of m
At reference strain rate, Eq. (1) can be expressed as
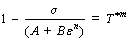 (5)
(5)
By taking natural logarithm of Eq. (5), Eq. (6) can be gained as follows:
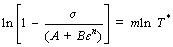 (6)
(6)
Using the flow stress at the same strain rate and strain but different temperatures to plot the curve ln[1-σ/(A+Bεn)] vs ln T* gives m from the slope of the curve. It should be noted that effective plastic strain in the JC model is used as a state variable for calculating work-hardening. In this work, the effective plastic strain is therefore calculated by subtracting the elastic portion from the true strain. By substituting the corresponding experimental data into Eqs. (3), (4) and (6), the relationships of ln(σ-A) vs ln ε, [σ/(A+Bεn)-1] vs 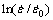 and ln[1-σ/(A+Bεn)] vs ln T* are obtained, respectively, as shown in Fig. 7. Then, the values of B, n, C and m are gained from the fitting curve, as summarized in Table 1. It is clear in Figs. 7(b) and (c) that the values of y-intercept for [σ/(A+Bεn)-1] vs
and ln[1-σ/(A+Bεn)] vs ln T* are obtained, respectively, as shown in Fig. 7. Then, the values of B, n, C and m are gained from the fitting curve, as summarized in Table 1. It is clear in Figs. 7(b) and (c) that the values of y-intercept for [σ/(A+Bεn)-1] vs 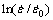 and ln[1-σ/(A+Bεn)] vs ln T* are not zero, which is against the requirements of Eqs. (4) and (6) that y-intercept must be zero.
and ln[1-σ/(A+Bεn)] vs ln T* are not zero, which is against the requirements of Eqs. (4) and (6) that y-intercept must be zero.
4.2 Results of JC model fitting
Using the parameters in Table 1, the flow stresses for the target materials were predicted by the JC model under various conditions. The comparisons between the experimental and predicted data are shown in Fig. 8. Obviously, the estimated values are not in good agreement with experimented data, especially at higher temperatures. This indicates that the JC model is inadequate to describe the flow behaviors of the target materials in the wide ranges of strain rates and temperatures.
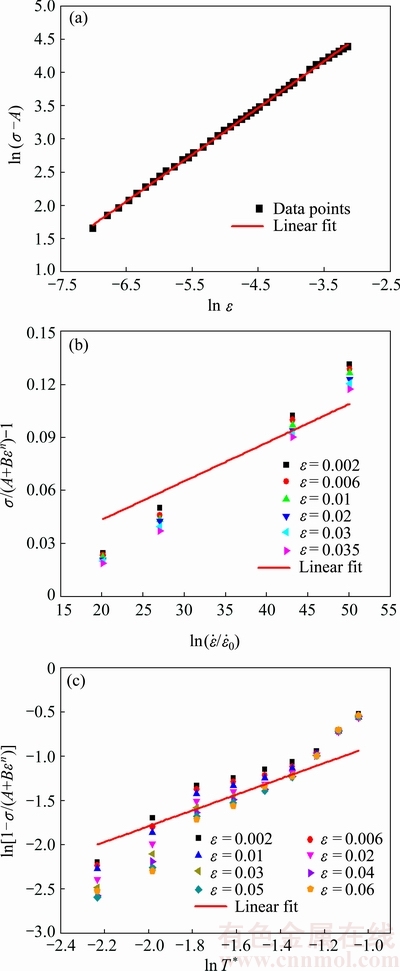
Fig. 7 Relationships of ln (σ-A) vs ln ε (a), [σ/(A+Bεn)-1] vs 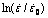 (b) and ln[1-σ/(A+Bεn)] vs ln T* (c)
(b) and ln[1-σ/(A+Bεn)] vs ln T* (c)
Table 1 Parameters of JC model for Ti-6Al-4V alloy

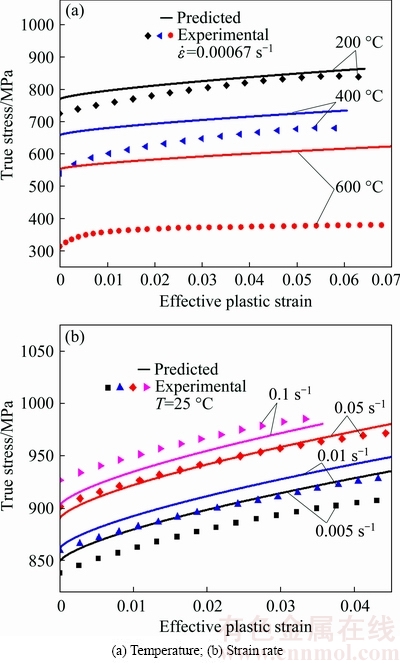
Fig. 8 Flow stress comparisons between experimental and predicted results by JC model
It is well known that the formulation of the JC model starts from an empirical basis and provides a fairly simple model, which may not always give precise predictions of flow stress, in particular, over wide ranges of strain rate and temperature [36-40]. This can be mainly attributed to the two shortcomings: 1) logarithmic function and power law function are unsuitable to fit the strain rate and temperature sensitivities of some materials since they determine a linear dependence of the yield stress on the natural logarithm of the dimensionless strain rate and temperature; 2) the effects of plastic strain, strain rate and temperature on the yield stress are totally independent. Hence, for a given equivalent plastic strain, its effect on the yield stress is the same whatever values the strain rate and temperature assume. This may cause heavy modeling errors as observed in Fig. 8.
4.3 Modification of JC model
4.3.1 Strain rate term
In the view of the two main shortcomings above, many researchers [36-41] have proposed modifications of the strain rate and temperature terms of the original JC model to improve the prediction precision. To date, the above-mentioned first issue of the JC model is partially solved or mitigated by the possibility of choosing different strain rate and temperature related terms so as to better fit the experimental data of the considered material. It is clear in Fig. 7(b) that the strain has almost no influence on the slope of [σ/(A+Bεn)-1] vs  , and thus there is no need to consider the effect of the strain on flow stress in the strain rate term. As a result, based on the work of HUH et al [42] and ULACIA et al [22], the quadratic term is added to the logarithmic strain rate term to correctly represent the effect of strain rate on flow stress in this work. Then, Eq. (1) becomes
, and thus there is no need to consider the effect of the strain on flow stress in the strain rate term. As a result, based on the work of HUH et al [42] and ULACIA et al [22], the quadratic term is added to the logarithmic strain rate term to correctly represent the effect of strain rate on flow stress in this work. Then, Eq. (1) becomes
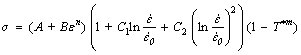 (7)
(7)
Following the same fitting procedure, C1 (0.0048) and C2 (0.004) are gained by the quadratic fit with the data of [σ/(A+Bεn)-1] vs  , as shown in Fig. 9. With the aid of Eq. (7), the flow stresses of the target material at different strain rates are predicted, and comparisons between the experimental and predicted results are shown in Fig. 10. Evidently, it can be observed that the material behavior is more accurately reproduced with the modified strain rate term not only at different strain rates but also at entire range of strain. This indicates that adding quadratic term to the logarithmic strain rate term is feasible for describing the change of flow stress with strain rate. Hence, there is no need to take into account the dependence of strain hardening parameter on strain rate in strain rate term of Eq. (7).
, as shown in Fig. 9. With the aid of Eq. (7), the flow stresses of the target material at different strain rates are predicted, and comparisons between the experimental and predicted results are shown in Fig. 10. Evidently, it can be observed that the material behavior is more accurately reproduced with the modified strain rate term not only at different strain rates but also at entire range of strain. This indicates that adding quadratic term to the logarithmic strain rate term is feasible for describing the change of flow stress with strain rate. Hence, there is no need to take into account the dependence of strain hardening parameter on strain rate in strain rate term of Eq. (7).
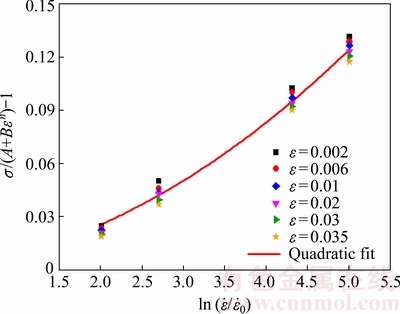
Fig. 9 Quadratic fit for data of [σ/(A+Bεn)-1] vs 
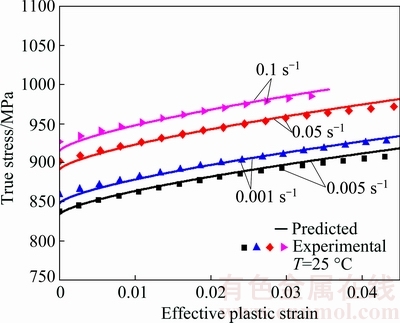
Fig. 10 Flow stress comparisons between experimental and predicted results by Eq. (7)
4.3.2 Temperature term
It is clear that the values of m, i.e. the slopes of the curves in Fig. 7(c), at different strains and temperatures are not a constant. Conversely, they are related to strain and temperature. That is against the initial assumption that m is a constant, never changing with the strain and temperature. Hence, a new model is proposed for better predictions based on Eq. (7) by modifying temperature term, i.e. accounting for the strain hardening change with temperature:
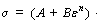
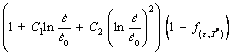 (8)
(8)
with
 (9)
(9)
where ai, bi, ci, di and ei (i=1, 2, 3, 4 and 5) are regression coefficients needed to be solved.
Firstly, according to the data of ln[1-σ/(A+Bεn)] vs ln T* shown in Fig. 11(a), the five coefficients (a-e) are solved. Subsequently, the changes of a, b, c, d and e with ε are obtained as shown in Fig. 11(b). From Fig. 11(b), ai, bi, ci, di and ei are determined directly by fitting. Now all the material constants in Eq. (8) for Ti-6Al-4V tube are obtained and given in Tables 2 and 3.
Using the parameters in Tables 2 and 3, the flow stress data for the target material are predicted using Eq. (8), and comparisons between the experimental and predicted results are shown in Fig. 12. Apparently, the modified JC model (Eq. (8)) provides good agreement with the experimental data in a wide range of temperature. In addition, this modified model captures the change of strain hardening with temperature.
4.3.3 Verifications and comparisons
In order to verify the modified JC model proposed in this work (i.e. Eq. (8)), new tensile experiments at different temperatures and strain rates were conducted.
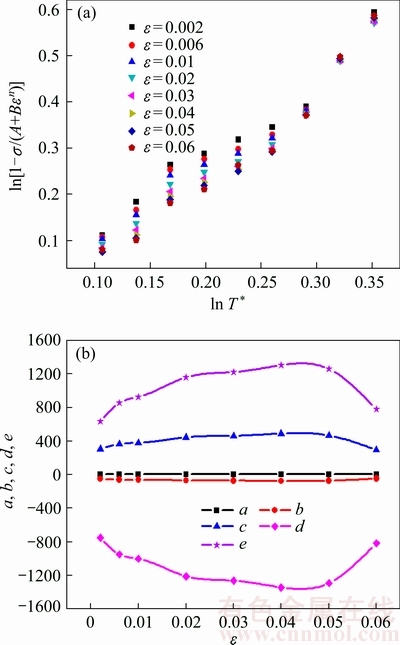
Fig. 11 Relationships of [1-σ/(A+Bεn)] vs ln T* (a), and five coefficients vs ε (b)
Table 2 Parameters of modified JC model for Ti-6Al-4V tube

Table 3 Parameters of f(ε, T*) in modified JC model

Comparison between the new experiment results and predicted results by Eq. (8) is shown in Fig. 13. It can be seen that the new modified JC model in this work also provides good agreement with all new experiments as observed in Figs. 9 and 11. Compared with the JC model, the parameters for Ti-6Al-4V tube are obtained by minimizing the relative errors of measured flow stress and calculated value by the model. The error of the predicted results and experimental results is quantified by employing statistical average absolute relative error (AARE) [43]. AARE is defined as
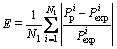 (10)
(10)
where 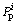 is the predicted value,
is the predicted value, 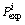 is the experimental value, and N is the total number of data. The AARE of the original JC model is about 10.7%, while the result of the modified JC model is about 1.2%. And the maximum error decreases from 30% to 3%. This clearly indicates that the modified JC model in this work is feasible to predict the flow behaviors of Ti-6Al-4V tube in a wide range of strain rates and temperatures.
is the experimental value, and N is the total number of data. The AARE of the original JC model is about 10.7%, while the result of the modified JC model is about 1.2%. And the maximum error decreases from 30% to 3%. This clearly indicates that the modified JC model in this work is feasible to predict the flow behaviors of Ti-6Al-4V tube in a wide range of strain rates and temperatures.
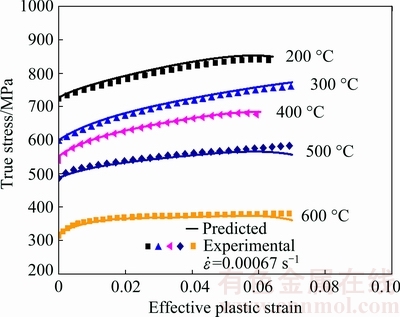
Fig. 12 Flow stress comparisons between experimental and predicted results by Eq. (8)
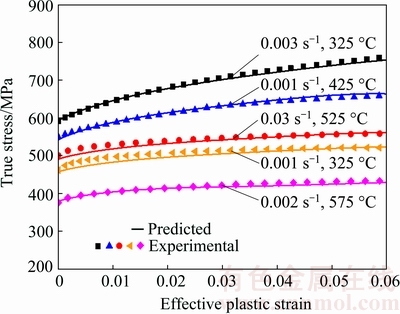
Fig. 13 Flow stress comparisons between new experimental and predicted results at different strain rates and temperatures
4.4 Application
The warm tube bending experiments are performed at different temperatures with modified W27YPC-159 tube bending equipment, as shown in Fig. 13.
Meanwhile, with the foundation of CP-Ti warm bending and cold tube bending [44], a 3D finite element (FE) model was developed to simulate the NC warm bending of the LDTW Ti-6Al-4V tube using ABAQUS platform. The 3D-FE model of NC warm bending includes the heat transfer process and the warm bending process. The detailed modeling issues can be found in Ref. [44]. The modified JC model proposed in this work was implemented into the FE code and the simulation of LDTW Ti-6Al-4V warm NC tube bending process was carried out.
The whole warm bending process was separated into two parts, as shown in Fig. 14: heating and bending. In the heating process, all of the dies were assembled with Ti-6Al-4V tube and were heated to proper temperature. In the bending process, Ti-6Al-4V tube, clamped by the clamp die and bend die, rotated along the bending die with mandrel filling inside to provide support and pressure die moving forward to provide boosting velocity.

Fig. 14 Simulation modeling of LDTW Ti-6Al-4V warm NC tube bending process
Figure 15 shows the simulated results and experimental parts after NC warm tube bending. The simulation results shown in Figs. 15(a, c, e) indicate that higher temperature brings about better deformation quality, which is in agreement with the material tensile tests. Then, the NC warm bending experiments under same conditions were carried out to compare with the simulation results, as shown in Figs. 15(b, d, f). As shown in Figs. 15(a) and (b), the evident stress concentration can be found especially at the extrados of the bending part, indicating the occurrence of fracture at the extrados of Ti-6Al-4V tube. Figures 15(c) and (d) exhibit that stress concentration at the inside of the bending part causes tube wrinkling. The comparison of simulation and experiment shows that the present model exhibits good ability to capture the deformation behaviors of Ti-6Al-4V LDTW tube over the entire temperature and strain rate ranges. As a result, the defects of over-thinning, wrinkling and fracture are predictable and the formation conditions of different kinds of defects can be well explained. The obtained results are very instructive for bending parameter optimization and process design. According to the results of high temperature tensile tests, proper bending temperature was set to be 500-600 °C and the FE simulations were further carried out. Resultantly, the steady bending of Ti-6Al-4V LDTW tube can be achieved in this temperature range without causing defects. Additionally, experimental results coincide well with the simulated ones, as illustrated in Figs. 15(e) and 15(f).

Fig. 15 Comparison of simulated and experimental results
In order to validate the reliability of the constitutive model, the wall thinning at the extrados and the wall thickening at the intrados of the preferable tube were used for comparison of experiment and the simulation results. Figure 16 shows the comparison of the wall thickness and wall thickening between experimental data and the predicted data by the modified constitutive model. Note that the definition of angle θ is illustrated in Fig. 16, representing the measured position in the tube. It can be seen that all the simulated results are very close to the experimental values. The maximum error of wall thinning ratio is 4% for LDTW Ti-6Al-4V warm NC tube bending at the bending angle of 65°, and the maximum error of wall thickening ratio is 2%, which are in the allowable range. Therefore, the established modified JC model is valid and reliable.
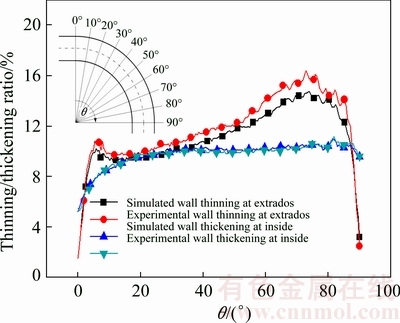
Fig. 16 Comparison of thinning/thickening ratio between experimental data and predicted data by modified JC model
5 Conclusions
1) Deformation behaviors of Ti-6Al-4V alloy have been characterized by SEM observations and constitutive analyses. Significant thermal softening and dramatically increased fracture strain, i.e., 4-5 times of the room temperature one, is exhibited at 600 °C and 0.00067 s-1. Correspondingly, homogeneous equiaxed grains rather than elongated grains are observable, indicating the change of deformation control mechanism from dislocation gliding to grain boundary sliding.
2) A modified JC model has been proposed by introducing nonlinear strain rate hardening and the interaction between strain hardening and thermal softening. In modeling, the temperature term is expressed by four strain related 3-order polynomials. Resultantly, the present model captures the variation features of temperature coefficient with strain which is failed to be predicted in original JC model, and thus maximum error decreases from 30% to 2%.
3) Applied to WRDB process, the present model exhibits good ability to capture the deformation behaviors of LDTW Ti-6Al-4V tube over the entire temperature and strain rate ranges, by successfully predicting the experimentally observed defects of over-thinning, wrinkling and fracture. The present work lays solid foundation for process optimization of NC WRDB forming of LDTW Ti-6Al-4V tube.
Acknowledgements
The authors would like to appreciate the help of Mr. Zhi-han ZHANG and Mr. Si-liang YAN for the model parameters calibration.
References
[1] BOYER R. An overview on the use of titanium in the aerospace industry [J]. Materials Science and Engineering A, 1996, 213(1-2): 103-114.
[2] LI Heng, YANG He, SONG Fei-fei, LI Guang-jun. Springback characterization and behaviors of high-strength Ti-3Al-2.5V tube in cold rotary draw bending [J]. Journal of Materials Processing Technology, 2012, 212(9): 1973-1987.
[3] BEAL J D, BOYER R, SANDERS D. Forming of titanium and titanium alloys [M]. Metalworking: Sheet Forming (ASM Handbook). 2006: 656-669.
[4] LI Xiao-qiang, GUO Gui-qiang, XIAO Jun-jie, SONG Nan, LI Dong-sheng. Constitutive modeling and the effects of strain-rate and temperature on the formability of Ti-6Al-4V alloy sheet [J]. Materials & Design, 2014, 55(6): 325-334.
[5] LIU Jaan-Ming, CHOU Sheh-Shon. Study on the microstructure and formability of commercially pure titanium in two-temperature deep drawing [J]. Journal of Materials Processing Technology, 1999, 95(1): 65-70.
[6] ZHANG Zhi-yong, YANG He, LI Heng, REN Ning, WANG Dan. Quasi-static tensile behavior and constitutive modeling of large diameter thin-walled commercial pure titanium tube [J]. Materials Science and Engineering A, 2013, 569(3): 96-105.
[7] ODENBERGER E L, PEDERSON R, OLDENBURG M. Thermo-mechanical material response and hot sheet metal forming of Ti-6242 [J]. Materials Science and Engineering A, 2008, 489(1-2): 158-168.
[8] LAI C P, CHAN L C, CHOW C L. Effects of tooling temperatures on formability of titanium TWBs at elevated temperatures [J]. Journal of Materials Processing Technology, 2007, 191(1-3): 157-160.
[9] KOTKUNDE N, DEOLE A D, GUPTA A K, SINGH S K. Experimental and numerical investigation of anisotropic yield criteria for warm deep drawing of Ti-6Al-4V alloy [J]. Materials & Design, 2014, 63(2): 336-344.
[10] ODENBERGER E L, SCHILL M, OLDENBURG M. Thermo-mechanical sheet metal forming of aero engine components in Ti-6Al-4VPART 2: Constitutive modeling and validation [J]. International Journal of Material Forming, 2012, 6(3): 391-402.
[11] THEPSONTHI T,  T. 3-D finite element process simulation of micro-end milling Ti-6Al-4V titanium alloy: Experimental validations on chip flow and tool wear [J]. Journal of Materials Processing Technology, 2015, 221: 128-145.
T. 3-D finite element process simulation of micro-end milling Ti-6Al-4V titanium alloy: Experimental validations on chip flow and tool wear [J]. Journal of Materials Processing Technology, 2015, 221: 128-145.
[12] LAI C P, CHAN L C, CHOW C L, YU K M. Thermal forming of light-weight alloys under a multi-stage forming process [J]. Journal of Mechanical Engineering Science, 2010, 224(4): 797-803.
[13] CHEN Guang, REN Cheng-zu, QIN Xu-da, LI Jun. Temperature dependent work hardening in Ti-6Al-4V alloy over large temperature and strain rate ranges: Experiments and constitutive modeling [J]. Materials & Design, 2015, 83: 598-610.
[14] KOTKUNDE N, DEOLE A D, GUPTA A K, SINGH S K, ADITYA B. Failure and formability studies in warm deep drawing of Ti-6Al-4V alloy [J]. Materials & Design, 2014, 60(8): 540-547.
[15] FIELDS D S, BACHOFEN W A. Determination of strain hardening characteristics by torsion testing [J]. Proceedings of ASTM International, 1957, 57: 1259-1272.
[16] KLOPP R W, CLIFTON R J, SHAWKI T G. Pressure-shear impact and the dynamic viscoplastic response of metals [J]. Mechanics of Materials, 1985, 4(3-4): 375-385.
[17] ZHANG Xian-hong, RUAN Xue-yu, OSAKADA K. Forgeability of AZ31B magnesium alloy in warm forging [J]. Transactions ofNonferrousMetals Society ofChina, 2003, 13(3): 632-635.
[18] CHENG Yong-qi, ZHANG Hui, CHEN Zhen-huang, XIAN Kui-feng. Flow stress equation of AZ31 magnesium alloy sheet during warm tensile deformation [J]. Journal of Materials Processing Technology, 2008, 208(1): 29-34.
[19] LIN Yong-cheng, CHEN Xiao-min. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials & Design, 2011, 32(4): 1733-1759.
[20] KOTKUNDE N, DEOLE A D, GUPTA A K, SINGH S K. Comparative study of constitutive modeling for Ti-6Al-4V alloy at low strain rates and elevated temperatures [J]. Materials & Design, 2014, 55(6): 999-1005.
[21] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Proceedings of the Seventh International Symposium on Ballistics. The Hague, Netherlands, 1983: 541-547.
[22] ULACIA I, SALISBURY C P, HURTADO I, WORSWICK M J. Tensile characterization and constitutive modeling of AZ31B magnesium alloy sheet over wide range of strain rates and temperatures [J]. Journal of Materials Processing Technology, 2011, 211(5): 830-839.
[23] CHEN Y, CLAUSEN A H, HOPPERSTAD O S, LANGSETH M. Stress-strain behavior of aluminum alloys at a wide range of strain rates [J]. International Journal of Solids & Structures, 2009, 46(21): 3825-3835.
[24] EI-MAGD E. Characterization, modeling and simulation of deformation and fracture behavior of the light-weight wrought alloys under high strain rate loading [J]. International Journal of Impact Engineering, 2006, 32(5): 741-758.
[25] LANGRAND B, GEOFFROY P, PETITNIOT J L, FABIS J, MARKIEWICZ E, DRAZETIC P. Identification technique of constitutive model parameters for crashworthiness modeling [J]. Aerospace Science and Technology, 1999, 3(4): 215-227.
[26] GAMBIRASIO L, RIZZI E. On the calibration strategies of the Johnson-Cook strength model: Discussion and applications to experimental data [J]. Materials Science and Engineering A, 2014, 610: 370-413.
[27] MILANI A S, DABBOUSSI W, NEMES J A, ABEYARATNE R C. An improved multi-objective identification of Johnson-Cook material parameters [J]. International Journal of Impact Engineering, 2008, 36(2): 294-302.
[28] KHAN A S, LIANG R. Behaviors of three BCC metal over a wide range of strain rates and temperatures: Experiments and modeling [J]. International Journal of Plasticity, 1999, 15(10): 1089-1109.
[29] KHAN A S, LIANG R. Behaviors of three BCC metals during non-proportional multi-axial loadings: Experiments and modeling [J]. International Journal of Plasticity, 2000, 16(12): 1443-1458.
[30] FARROKH B, KHAN A S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling [J]. International Journal of Plasticity, 2009, 25(5): 715-732.
[31] PEIRS J, TIRRY W, AMIN-AHMADI B, COGHE F, VERLEYSEN P, RABET L, SCHRYVERS D, DEGRIECK J. Microstructure of adiabatic shear bands in Ti6Al4V [J]. Materials Characterization, 2013, 75(2): 79-92.
[32] ZHANG X P, SHIVPURI R, SRIVASTAVA A K. Role of phase transformation in chip segmentation during high speed machining of dual phase titanium alloys [J]. Journal of Materials Processing Technology, 2014, 214(12): 3048-3066.
[33] JOSHI S, PAWAR P, TEWARI A, JOSHI S S. Influence of β phase fraction on deformation of grains in and around shear bands in machining of titanium alloys [J]. Materials Science and Engineering A, 2014, 618: 71-85.
[34] SCHNEIDER J, DONG L, HOWE J Y, MEYER H M III. Microstructural characterization of Ti-6Al-4V metal chips by focused ion beam and transmission electron microscopy [J]. Metallurgical & Materials Transactions A, 2011, 42(11): 3527-3533.
[35] ZHEREBTSOV S, MURZINOVA M, SALISHCHEV G, SEMIATIN S L. Spheroidization of the lamellar microstructure in Ti-6Al-4V alloy during warm deformation and annealing [J]. Acta Materialia, 2011, 59(10): 4138-4150.
[36] CAI Jun, WANG Kuan-she, ZHAI Peng, LI Fu-guo, YANG Jie. A modified Johnson-Cook constitutive equation to predict hot deformation behavior of Ti-6Al-4V alloy [J]. Journal of Materials Engineering & Performance, 2014, 24(1): 32-44.
[37] HOGE K G, MUKHERJEE A K. The temperature and strain rate dependence of the flow stress of tantalum [J]. Journal of Materials Science, 1977, 12(8): 1666-1672.
[38] HOLMQUIST T J, JOHNSON G R. Determination of constants and comparison of results for various constitutive models [J]. Journal De Physique IV, 1991, IV 1(C3): 299-306.
[39] KOTKUNDE N, KRISHNAMURTHY H N, PURANIK P, GUPTA A K,SINGH S K. Microstructure study and constitutive modeling of Ti-6Al-4V alloy at elevated temperatures [J]. Materials & Design, 2014, 54(2): 96-103.
[40] NEMAT-NASSER S, GUO W G. Thermomechanical response of DH-36 structural steel over a wide range of strain rates and temperatures [J]. Mechanics of Materials, 2003, 35(11): 1023-1047.
[41] GAMBIRASIO L, RIZZI E. An enhanced Johnson-Cook strength model for splitting strain rate and temperature effects on lower yield stress and plastic flow [J]. Computational Materials Science, 2016, 113: 231-265.
[42] HUH H, KANG W J, HAN S S. A tension split Hopkinson bar for investigating the dynamic behavior of sheet metals [J]. Experimental Mechanics, 2002, 42(1): 8-17.
[43] CAI Jun, LI Fu-guo, LIU Tai-ying, CHEN Bo. Microindentation study of Ti-6Al-4V alloy [J]. Materials & Design, 2011, 32(5): 2756-2762.
[44] ZHANG Zhi-yong, YANG He, LI Heng, TAO Zhi-jun, WANG Dan. Thermo-mechanical coupled 3D-FE modeling of heat rotary draw bending for large-diameter thin-walled CP-Ti tube [J]. The International Journal of Advanced Manufacturing Technology, 2014, 72(9-12): 1187-1203.
陶智君,樊晓光,杨 合,马 俊,李 恒
西北工业大学 材料学院 凝固技术国家重点实验室,西安 710072
摘 要:大口径薄壁Ti-6Al-4V管是航空航天等高端制造领域亟需的典型轻量化高性能构件,数控温弯能够有效实现大口径Ti-6Al-4V管的精确成形。由于数控温弯工艺过程是多场耦合复杂变形过程,建立其材料本构模型并实现全过程有限元模拟是亟待解决的瓶颈技术。利用管材单向拉伸实验,结合温弯工艺参数变化,研究温度在25~600 °C和应变速率在0.00067~0.1 s-1情况下Ti-6Al-4V管的力学性能。考虑非线性硬化率和应变的交互作用,建立了修正的Johnson-Cook本构模型,并根据实验数据对相关修正参数进行了拟合。将该模型应用于温弯模拟中可发现,修正的JC模型与传统的模型相比,可降低最大误差90%,并且可以有效预测管材断裂、起皱等成形缺陷发生的位置,为大口径薄壁Ti-6Al-4V管数控温弯成形极限和工艺优化奠定基础。
关键词:数控温弯;Ti-6Al-4V管;Johnson-Cook本构模型
(Edited by Bing YANG)
Foundation item: Projects (50905144, 51275415) supported by the National Natural Science Foundation of China; Project supported by the Program for New Century Excellent Talents in University, China; Project (3102014KYJD001) supported by Fundamental Research Funds for the Central Universities, China; Project (B08040) supported by Program of Introducing Talents of Discipline to Universities (“111” Project), China
Corresponding author: Xiao-guang FAN; Tel: +86-29-88495632; Fax: +86-29-88460212; E-mail: fxg3200@nwpu.edu.cn
DOI: 10.1016/S1003-6326(18)64663-1

