Particle swarm optimization algorithm for simultaneous optimal placement and sizing of shunt active power conditioner (APC) and shunt capacitor in harmonic distorted distribution system
来源期刊:中南大学学报(英文版)2017年第9期
论文作者:Mohammadi Mohammad
文章页码:2035 - 2048
Key words:shunt capacitor banks; active power conditioner; multi-objective function; particle swarm optimization (PSO); harmonic distorted distribution system
Abstract: Due to development of distribution systems and increase in electricity demand, the use of capacitor banks increases. From the other point of view, nonlinear loads generate and inject considerable harmonic currents into power system. Under this condition if capacitor banks are not properly selected and placed in the power system, they could amplify and propagate these harmonics and deteriorate power quality to unacceptable levels. With attention of disadvantages of passive filters, such as occurring resonance, nowadays the usage of this type of harmonic compensator is restricted. On the other side, one of parallel multi-function compensating devices which are recently used in distribution system to mitigate voltage sag and harmonic distortion, performs power factor correction, and improves the overall power quality as active power conditioner (APC). Therefore, the utilization of APC in harmonic distorted system can affect and change the optimal location and size of shunt capacitor bank under harmonic distortion condition. This paper presents an optimization algorithm for improvement of power quality using simultaneous optimal placement and sizing of APC and shunt capacitor banks in radial distribution networks in the presence of voltage and current harmonics. The algorithm is based on particle swarm optimization (PSO). The objective function includes the cost of power losses, energy losses and those of the capacitor banks and APCs.
Cite this article as: Mohammadi Mohammad. Particle swarm optimization algorithm for simultaneous optimal placement and sizing of shunt active power conditioner (APC) and shunt capacitor in harmonic distorted distribution system [J]. Journal of Central South University, 2017, 24(9): 2035–2048. DOI: https://doi.org/10.1007/s11771- 017-3613-7.
J. Cent. South Univ. (2017) 24: 2035-2048
DOI: https://doi.org/10.1007/s11771-017-3613-7

Mohammadi Mohammad
Department of Electrical Engineering, Borujerd Branch, Islamic Azad University, Borujerd, Iran
 Central South University Press and Springer-Verlag GmbH Germany 2017
Central South University Press and Springer-Verlag GmbH Germany 2017
Abstract: Due to development of distribution systems and increase in electricity demand, the use of capacitor banks increases. From the other point of view, nonlinear loads generate and inject considerable harmonic currents into power system. Under this condition if capacitor banks are not properly selected and placed in the power system, they could amplify and propagate these harmonics and deteriorate power quality to unacceptable levels. With attention of disadvantages of passive filters, such as occurring resonance, nowadays the usage of this type of harmonic compensator is restricted. On the other side, one of parallel multi-function compensating devices which are recently used in distribution system to mitigate voltage sag and harmonic distortion, performs power factor correction, and improves the overall power quality as active power conditioner (APC). Therefore, the utilization of APC in harmonic distorted system can affect and change the optimal location and size of shunt capacitor bank under harmonic distortion condition. This paper presents an optimization algorithm for improvement of power quality using simultaneous optimal placement and sizing of APC and shunt capacitor banks in radial distribution networks in the presence of voltage and current harmonics. The algorithm is based on particle swarm optimization (PSO). The objective function includes the cost of power losses, energy losses and those of the capacitor banks and APCs.
Key words: shunt capacitor banks; active power conditioner; multi-objective function; particle swarm optimization (PSO); harmonic distorted distribution system
1 Introduction
Capacitor placement in distribution networks for reactive power compensation, voltage regulation, power factor correction, and power/energy loss reduction has been extensively researched and documented in Refs. [1-5]. Some researchers have assumed linear system loads and used power flow for system solution [2-5]. However, limited attention is given to this problem in the presence of non-linear loads.
Nonlinear loads and devices generate and inject considerable harmonic currents into power system. If (shunt) capacitor banks are not properly selected and placed in the power system, they could amplify and propagate these harmonics and deteriorate power quality to unacceptable levels, resulting in creation of harmonic parallel resonances. Therefore, analyses, simulation, and optimal selection of capacitor banks under harmonic conditions are required in distribution networks.
The harmonics lead to a higher capacitor current, resulting in failure of capacitor in the power system network. Harmonic distortion can also affect the operation of power system components in a network, such as nuisance tripping of circuit breakers and other protective devices, failure or malfunctioning of motor drives and even malfunctioning of computers and lighting circuits.
The shunt capacitors are applied for reactive power compensation locally to reduce the power loss and sustain the voltage profile within an acceptable operating limit. The shunt capacitors can be considered as redundant lines in the system inasmuch reducing the reactive current leads to enhancing load-carrying capability of the lines, as discussed in Ref. [6]. Therefore, they can also improve the system reliability. In a real distribution network, harmonic distortion levels are high due to harmonic injection by non-linear loads. If the harmonic sources in the system are not considered in capacitor placement, it may lead to an increase in harmonic distortion levels due to resonance between shunt capacitors and the various inductive elements in the system. In Ref. [7], optimal placement of shunt capacitor was applied to reduce the total cost of power loss and capacitor installation as well as the harmonic distortion level, using fast harmonic power flow method presented in Ref. [8].
Installing some components, such as distributed generation, passive harmonic filters, active filters, DFACTS devices and reconfiguration feeder network, alters the impedance structure of the network, so it affects the network harmonic distortion level. This mainly can affect and change the optimal location and size of shunt capacitor bank in a harmonic distorted system.
One of custom power devices which are recently used in distribution system to improve power quality is APC. It is a parallel multi-function compensating device, which, depending on the available controller design, is able to mitigate voltage sag and harmonic distortion, perform power factor correction, and improve the overall power quality. APC has the potential to reduce harmonic distortion, transient voltage spikes and flicker by injecting equal but opposite distortion. APC employs power electronic devices to rapidly switch dc sources, synthesizing the chopped injection current waveform needed to compensate for existing voltage or current distortion [9]. Compared with the traditional harmonic compensation devices, APC has main advantages, such as the ability to mitigate voltage sag and harmonic distortion, performs power factor correction, and improve the overall power quality without the operational problems such as occurring resonance and using large number of filters required unlike shunt passive filters. Therefore, the utilization of APC can affect and change the optimal location and size of shunt capacitor bank in a harmonic distorted system. Some researchers have considered two or more items in capacitor placement. In Refs. [10, 11], the reconfiguration and capacitor placement are employed simultaneously to reduce the power loss. A sensitivity index-based methodology is presented in Ref. [12] to minimize the energy loss using network reconfiguration combined with capacitor allocation. Nonetheless,in previous papers such as Refs. [10-12], the reconfiguration and capacitor placement were performed without harmonics consideration. In Ref. [13] used combinatorial form of local searching and GA was for solving placing problems of DGs and capacitor simultaneously which is considered in radial distribution network with different load levels. In Ref. [14] authors provided a novel method for reaching optimal answer of locating and sizing for capacitors and DGs simultaneously in distribution systems as a multi- objective optimization problem. PSO based placement of multiple wind DGs and capacitors utilizing probabilistic load flow model was addressed in Ref. [15]. However, the effects of nonlinear load and harmonics have not considered in Ref. [10-15]. Newly some studies have investigated the capacitor placement in harmonic distorted distribution system. For instance authors have presented a new method for optimal location and sizing of capacitors in harmonic distorted distribution networks using PSO algorithm [16]. In Ref [17], authors proposed the fuzzy optimal placement of capacitors in the presence of nonlinear loads in unbalanced distribution networks using BF-PSO algorithm. In Ref. [18], a new method has been suggested to determine the optimal capacitor placement and sizing, taking into account fixed capacitors as well as potential harmonic interactions (losses, resonance and distortion factors) in the presence of distributed generators using GA.
However, the effect of utilization of custom power devices such as active power conditioner and other harmonic compensator equipment which have effective role in the harmonics content and harmonic routes in distribution systems have not been considered in the capacitor placement. Few researches have investigated the APC placement without considering the effect of shunt capacitor banks. In Ref. [19], the authors have proposed a new method to optimize the placement and size of multiple active power conditioners (APCs) with the objectives of minimizing the investment cost, while the voltage total harmonic distortion and the individual harmonic distortion were considered constraints.An improved solution for optimum placement of active power conditioner in distribution systems using improved discrete firefly algorithm for power quality enhancement has been presented in Ref. [20].
As reviewed in Refs. [9, 19, 20] with attention of APC capabilities in power loss and harmonic reduction, the presence of this device in distribution system can affect the capacitors placement problem. Therefore, to achieve a more effective planning and better management of the harmonic problem in the distribution system, the simultaneous placement and sizing of these two devices (shunt capacitor banks and active power conditions) could be analyzed.
This work presents an optimization algorithm for improvement of power quality using simultaneous optimal placement and sizing of APC and shunt capacitor banks in radial distribution networks in the presence of voltage and current harmonics. The algorithm is based on particle swarm optimization (PSO). The objective function includes the cost of power losses, energy losses and those of the capacitor banks and APCs.
2 Modeling of active power conditioner
APC is a parallel multi-function compensating device, which, depending on the available controller design, is able to mitigate voltage sag and harmonic distortion, perform power factor correction, and improve the overall power quality. The voltage-source converter is the main part of the APC, which converts the dc-link voltage into three-phase ac voltages with controllable amplitude, frequency and phase. Considering the steady-state APC losses such as transformer and inverter losses, an accurate load flow model of the APC should be obtained.
Figure 1 shows the schematic diagram of an APC and its Norton equivalent circuit with respect to bus N.
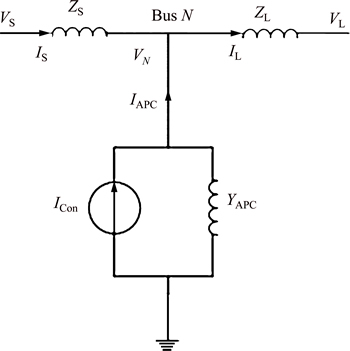
Fig.1 APC single-line Norton equivalent circuit
From the figure, the injected current IAPC at bus N in fundamental and harmonic frequencies can be expressed as
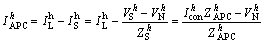 (1)
(1)
where IAPC is the injected current by APC with phase angle δi; Icon is the Norton current with phase angle δcon; IS is the utility side current with phase angle θi; VS is the utility side voltage with phase angle θv; VN is the voltage at bus N with phase angle θv-N-; IL is the load side current with phase angle λi; ZS is the utility impedance; ZAPC is APC Norton impedance (1/YAPC); h is harmonic orders, like 1, 2, 3, …, H.
Equation (1) shows that the injected APC current  can correct voltage sag, voltage variation and harmonic distortion at bus N by adjusting the voltage drop across the impedance ZAPC in the fundamental and harmonic frequencies.
can correct voltage sag, voltage variation and harmonic distortion at bus N by adjusting the voltage drop across the impedance ZAPC in the fundamental and harmonic frequencies.
To compute the bus voltage variations in fundamental and harmonic frequencies in the presence of APC, it is assumed that APC is added to the system as a PQ bus (the bus with the specified real power |P| and reactive power |Q|) with impedance  between the existing bus N and the newly added virtual bus K in a M-bus system.
between the existing bus N and the newly added virtual bus K in a M-bus system.
Therefore, the new impedance matrix of the system should be modified based on  as [21]
as [21]
 (2)
(2)
The new column accounts for the increase of all bus voltages due to  . Considering virtual bus K is short circuited to the reference node, the virtual bus K can be eliminated using the Kron reduction method on Eq. (2) as
. Considering virtual bus K is short circuited to the reference node, the virtual bus K can be eliminated using the Kron reduction method on Eq. (2) as
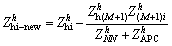 (3)
(3)
Hence, the bus voltages calculated at the fundamental and harmonic frequencies due to the presence of APC can be obtained using the modified impedance matrix as
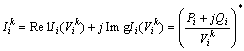 (4)
(4)
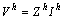 (5)
(5)
where 

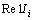 and
and 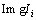 are the node voltage at the kth iteration, equivalent current injection at the kth iteration, and the real and imaginary parts of the equivalent current injection at the kth iteration, respectively. In addition, [V], [Z] and [I] are the bus voltage vector, system impedance matrix, and nodal injected current vector in fundamental and harmonic frequency, respectively.
are the node voltage at the kth iteration, equivalent current injection at the kth iteration, and the real and imaginary parts of the equivalent current injection at the kth iteration, respectively. In addition, [V], [Z] and [I] are the bus voltage vector, system impedance matrix, and nodal injected current vector in fundamental and harmonic frequency, respectively.
Equations (4) and (5) can be solved using the backward/forward sweep method [22, 23]. Note that the values of P and Q in Eq. (4) are positive for conventional PQ (load) buses and negative for bus with APC. The bus voltage at bus i in the fundamental and harmonic frequencies and the voltage THD can be changed by altering the rating of the installed APC during the optimization process.
3 Multi-objective problem formulation
The optimal APC and shunt capacitor placement and sizing problem as simultaneously in this work is essentially a multi-objective optimization problem, which aims to simultaneously enhance power quality and minimize the total investment costs of the active power conditioners and shunt capacitors in the system.Therefore, the problem is designed in terms of a single- objective function which comprises of three sub- functions and five constraints representing the control variables as follows.
3.1 Minimizing total cost
The first objective function is investment cost of the active power conditioners and shunt capacitors and is calculated as follows:
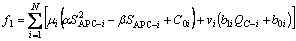 (6)
(6)
where N is the total number of buses; μi and videcide whether to install active power conditioner and shunt capacitor; μi,=1 represents a connection of APC at bus i; μi,=0 means no installation in the bus; vi=1 indicates a connection of shunt capacitor at bus i; vi=0 means no installation in the bus. SAPC-i demonstrates the capacity of the APC in bus i; QC-i is the reactive capacity size of shunt capacitor in bus i. Also, C0i is fixed installation cost of APC and b1i is the annual cost of the reactive power injection at bus i and b0i is fixed installation cost of capacitor. In addition, α and β are fixed coefficients,which are assumed in this work as 0.0002466 and 0.2243,respectively.
3.2 Minimizing total harmonic distortion of bus voltage
The second objective function is minimizing total harmonic distortion.
 (7)
(7)
where h is the harmonic order; U1i is the fundamental effective voltage at bus i; Uhi is the harmonic effective voltage at bus i; THDu,i is total harmonic voltage distortion at bus i; U1i and Uhi are gained by power flow calculation.
3.3 Minimizing total power loss
The third-objective function is power loss minimization under harmonic distorted environment and is formulated as follows [24]:

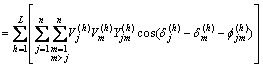 (8)
(8)
where  and
and  are magnitude and phase of the hth harmonic voltage at bus j, respectively;
are magnitude and phase of the hth harmonic voltage at bus j, respectively;  and
and 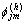 are also magnitude and phase of hth harmonic line admittance between buses j and m, respectively.
are also magnitude and phase of hth harmonic line admittance between buses j and m, respectively.
First to normalize three mentioned objective functions, Eqs. (6), (7) and (8) are normalized as follows:
 (9)
(9)
 (10)
(10)
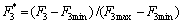 (11)
(11)
where F1*, F2* and F3* respectively presents the normalized value of f1, f2 and f3, which are reduced in (0-1). Then the linear weight is used to construct a multi-objective function.
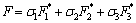 (12)
(12)
where σ1, σ2 and σ3 are weights of Eqs. (9), (10) and (11), σ1+σ2+σ3=1.
4 Problem constraints
4.1 Bus voltage limits
Voltage constraints will be taken into account by specifying lower (e.g., Vmin=0.9 pu) and upper (e.g., Vmax=1.1 pu) bounds of effective voltage (e.g., V) as below:
 (13)
(13)
where RMS magnitude voltage is:
 (14)
(14)
so that i and k, are the bus number and harmonic orders, respectively.
4.2 APC capacity limits
Considering that the APC capacity is inherently limited by the energy resources at any given location, the capacity has to be constrained within a permissible band, specified as [SAPC-min, SAPC-max], where SAPC-min and SAPC-max are the minimum and maximum permissible values of each APC capacity, respectively. These limits can be expressed in terms of an inequality function as
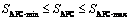 (15)
(15)
4.3 Shunt capacitor constraints
Shunt capacitors that are available in the industry are shown by Eq. (16), where L is an integer number and Q0 is the smallest available capacitor size.
 (16)
(16)
Moreover, due to economic problems and limited installation space, the maximum allowable capacitance at the buses should not be beyond the allowable constraint.
 (17)
(17)
4.4 Power flow limits
The apparent power Sl transmitted through branch l must not exceed its maximum thermal limit Sl-max in the steady state operation as
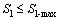 (18)
(18)
4.5 Shunt capacitors and APCs number limits
Let  denote the maximum number of shunt capacitors and active power conditioner allowed at the entire feeder, respectively. Hence, the number of capacitors and active power conditioner becomes limited by the following equation:
denote the maximum number of shunt capacitors and active power conditioner allowed at the entire feeder, respectively. Hence, the number of capacitors and active power conditioner becomes limited by the following equation:
 (19)
(19)
 (20)
(20)
5 Harmonic power flow
Harmonic power flow calculation is a basic calculation in this work, which would be repeatedly used many times throughout the optimal process. It is the purpose of computing buses harmonic voltage, current and the total voltage harmonic distortion in the system that provides theoretical basis for judging whether the proposed schemes from the filters optimization meet the harmonic distortion constraints.
Analysis methods of harmonic power flow mainly include nonlinear time domain analysis, frequency domain analysis and linear analysis. The linear analysis method has characters as quick computing speed, good convergence, simple programming, making it the most commonly used method. The steps of utilizing the linear analysis method of harmonic power flow in this paper are as follows.
5.1 Fundamental power flow calculation
Fundamental power flow is calculated for obtaining the fundamental voltages and the load of each bus, using Matpower components.
5.2 Formation of harmonic bus admittance matrix
The most of the distribution feeders are radial. Generically, each bus can have linear and nonlinear loads, and shunt capacitor banks.
To determine the harmonic flow in a radial distribution feeder, the current injection method can be used [25]. The advantages of this method are that solution can be obtained directly. It is able to handle several harmonic sources simultaneously, and it is computationally efficient. In this method, the network harmonic voltages are calculated by frequency-domain matrix:
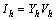 (21)
(21)
where Ih is the Harmonic current injection vector; Vh is the Harmonic voltage vector to be calculated; and Yh is the admittance matrix of the system. In the adopted notation, the superscript h assumes all values of harmonic orders of interest. The superscript 1 (h=1) corresponds to parameters in fundamental frequency.
The elements of admittance matrix should use models whose parameters are frequency-dependent. However, there is some disagreement regarding which harmonic models are the best for each component of system [26].
The admittances of each line feeder section and capacitor banks in end of each section are:
 (22)
(22)
and
 (23)
(23)
where Ri and Xi the resistance and the inductive reactance of feeder section i and 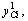 it is the shunt admittance of the capacitor bank in the bus i, in the fundamental frequency.
it is the shunt admittance of the capacitor bank in the bus i, in the fundamental frequency.
The linear loads are represented by a parallel combination of resistance and inductive reactance. These parameters are obtained through the load data in fundamental frequency. The harmonic admittance of these loads is given by
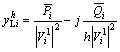 (24)
(24)
In that  and
and  they are the active and reactive powers of the linear loads in the bus i.
they are the active and reactive powers of the linear loads in the bus i.
The nonlinear loads are represented by harmonic currents sources whose nominal values to the fundamental frequency are:
 (25)
(25)
where 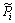 and
and 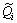 are the active and reactive power of the nonlinear load in the ith bus. In harmonic frequencies, the current source has nominal values:
are the active and reactive power of the nonlinear load in the ith bus. In harmonic frequencies, the current source has nominal values:
 (26)
(26)
where  the percentile value of the current, in the hth harmonic order.
the percentile value of the current, in the hth harmonic order.
5.3 Solution for harmonic power flow
With the determined admittance matrix and the injection harmonic current, the harmonic voltages and currents of the system can be calculated by the following array formula:
 (27)
(27)
where Ih is the injection harmonic currents column vector, in which bus without harmonic source is zero and the nonzero elements are injection harmonic current Iih and Uh is harmonic voltages column vector.
The flowchart of optimal location and sizing of shunt capacitors and active power conditioner is proposed in Fig. 2.
6 Particle swarm optimization (PSO) algorithm
Particle swarm optimization algorithm, which is tailored for optimizing difficult numerical functions and based on metaphor of human social interaction, is capable of mimicking the ability of human societies to process knowledge [27]. It has roots in two main component methodologies: artificial life (such as bird flocking, fish schooling and swarming); and evolutionary computation. Its key concept is that potential solutions are flown through hyperspace and are accelerated towards better or more optimum solutions. Its paradigm can be implemented in simple form of computer codes and is computationally in expensive in terms of both memory requirements and speed. It lies somewhere in between evolutionary programming and the genetic algorithms. As in evolutionary computation paradigms, the concept of fitness is employed and candidate solutions to the problem are termed particles or sometimes individuals, each of which adjusts its flying based on the flying experiences of both itself and its companion. It keeps track of its coordinates in hyperspace which is associated with its previous best fitness solution, and also of its counterpart corresponding to the overall best value acquired thus far by any other particle in the population. Vectors are taken as presentation of particles since most optimization problems are convenient for such variable presentations. In fact, the fundamental principles of swarm intelligence are adaptability, diverse response, proximity, quality, and stability. It is adaptive corresponding to the change of the best group value. The allocation of responses between the individual and group values ensures a diversity of response. The higher dimensional space calculations of the PSO concept are performed over a series of time steps. The population is responding to the quality factors of the previous best individual values and the previous best group values. The principle of stability is adhered to since the population changes its state if and only if the best group value changes. As reported in Ref. [28], this optimization technique can be used to solve many of the same kinds of problems as GA, and does not suffer from some of gas difficulties. It has also been found to be robust in solving problem featuring non-linearity, non-differentiability and high-dimensionality. PSO is the search method to improve the speed of convergence and find the global optimum value of fitness function.
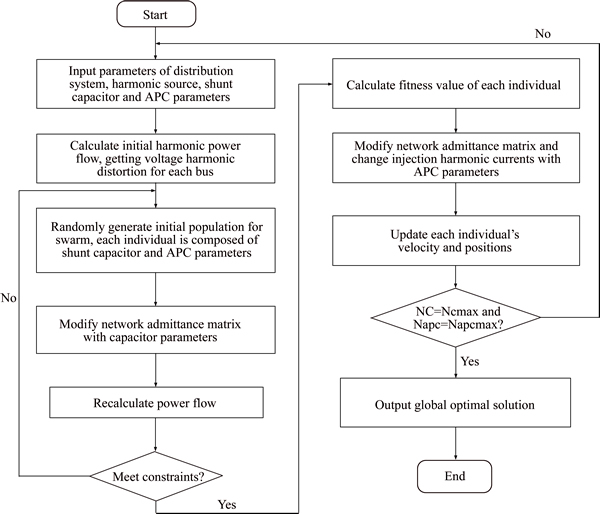
Fig. 2 Flowchart of optimal location and sizing of shunt capacitors and active power conditioner
PSO starts with a population of random solutions ‘‘particles’’ in a D-dimensional space. The ith particle is represented by  Each particle keeps track of its coordinates in hyperspace, which is associated with the fittest solution that it has achieved so far. The value of the fitness for particle i (pbest) is also stored as
Each particle keeps track of its coordinates in hyperspace, which is associated with the fittest solution that it has achieved so far. The value of the fitness for particle i (pbest) is also stored as 
The global version of the PSO keeps track of the overall best value (gbest), and its location obtained thus far by any particle in the population. PSO consists of, at each step, changing the velocity of each particle toward its pbest and gbest according to Eq. (28). The velocity of particle i is represented 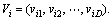
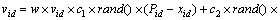
 (28)
(28)
Acceleration is weighted by a random term, with separate random numbers being generated for acceleration toward pbest and gbest. The position of the ith particle is then updated according to Eq. (29) [27].
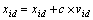 (29)
(29)
where Pid and Pgd are pbest and gbest. Several modifications have been proposed in the literature to improve the PSO algorithm speed and convergence toward the global minimum. One modification is to introduce a local-oriented paradigm (lbest) with different neighborhoods. It is concluded that gbest version performs best in terms of median number of iterations to converge. However, pbest version with neighborhoods of two is most resistant to local minima. PSO algorithm is further improved via using a time-decreasing inertiaon weight, which leads to a reduction in the number of iterations [28]. Figure 3 shows the flowchart of the proposed PSO algorithm.
This new approach features many advantages: it is simple, fast and easy to be coded. Also, its memory storage requirement is minimal. Moreover, this approach is advantageous over evolutionary and genetic algorithms in many ways. First, PSO has memory. That is, every particle remembers its best solution (local best) as well as the group best solution (global best). Another advantage of PSO is that the initial population of the PSO is maintained, and so there is no need for applying operators to the population, a process that is time- and memory-storage consuming. In addition, PSO is based on ‘‘constructive cooperation’’ between particles; In contrast with the genetic algorithms, it is based on “the survival of the fittest”.

Fig. 3 Flowchart of proposed PSO technique
7 Application of PSO to proposed problem
7.1 Swarm structure
In this paper, the swarm structure for PSO consists of SC values, where SC denotes the number of possible buses for capacitor placement in the entire feeder. These numbers indicate the size of the installed capacitor at the bus under consideration.
7.2 Proposed fitness function
The algebraic product of proposed penalty functions is used as the new fitness function to combine the objective and constraint functions, and reduce power losses according to the following relationship:
 (30)
(30)
where F is the objective function (Eq. (12)). A combination of 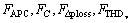 and F is used to improve population and convergence of the solution in consecutive generations. This proposed fitness function will automatically eliminate all solutions generating extreme values for total harmonic distortion, number of capacitor and active power conditioner allocated at buses, and power losses. In the problem considered in this article, attempt has been made to reduce the objective function, while the problem constraints are mostly satisfied. The swarms with lower fitness function are then used to generate the next population. By this procedure, the next population will be regenerated so that in addition to minimizing objective function, the problem constraints will be satisfied.
and F is used to improve population and convergence of the solution in consecutive generations. This proposed fitness function will automatically eliminate all solutions generating extreme values for total harmonic distortion, number of capacitor and active power conditioner allocated at buses, and power losses. In the problem considered in this article, attempt has been made to reduce the objective function, while the problem constraints are mostly satisfied. The swarms with lower fitness function are then used to generate the next population. By this procedure, the next population will be regenerated so that in addition to minimizing objective function, the problem constraints will be satisfied.
The  factor is applied for controlling the THD of buses voltage. If THD voltages were less than or equal to 5% (i.e.
factor is applied for controlling the THD of buses voltage. If THD voltages were less than or equal to 5% (i.e. 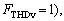 the optimization could be achieved [29]; otherwise for
the optimization could be achieved [29]; otherwise for 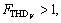 the corresponding swarm would be further away in the following optimization process. This factor is defined as
the corresponding swarm would be further away in the following optimization process. This factor is defined as
 (31)
(31)
The  factor is applied for decreasing the total power losses in distribution systems. If total power loss change is greater than zero, the optimization could be achieved; otherwise for
factor is applied for decreasing the total power losses in distribution systems. If total power loss change is greater than zero, the optimization could be achieved; otherwise for 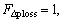 the corresponding swarm would be again further away in the optimization process. This factor is defined as
the corresponding swarm would be again further away in the optimization process. This factor is defined as
 (32)
(32)
The FC factor is applied for decreasing the total number of capacitor allocated at buses. If total number of capacitors was less than or equal to the maximum total number of capacitor allowed at each buses, FC is equal to unity and the optimization is achievable; otherwise for FC>1, the corresponding chromosome would be eliminated in the following optimization process. This factor is defined as
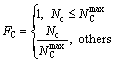 (33)
(33)
The FAPC factor is applied for decreasing the total number of active power conditioner allocated at buses. If total number of capacitors was less than or equal to the maximum total number of active power conditioners allowed at each buses, FAPC is equal to unity, the optimization is achievable; otherwise for FAPC>1, the corresponding chromosome would be eliminated in the following optimization process. This factor is defined as
 (34)
(34)
7.3 Convergence criterion
The iterations of the PSO algorithm are continued until the maximum number of iterations is achieved. In addition, the initial generation procedure of swarm and iterations of algorithm consists of improving particles and regeneration of swarm in the course of several steps such that the operational and PQ constraints are maintained within required limits.
8 Simulation and test results
To verify the effectiveness and applicability of the proposed PSO on radial distorted distribution systems, the IEEE 15-bus and IEEE 33-bus test systems are modified and shown in Figs. 4 and 5 respectively [30, 31].
In the IEEE 15-bus test system, a non-linear load as six-pulse rectifier with active and reactive powers of 0.07 pu (0.7 MW) and 0.055 pu (0.55 MVar), respectively, is connected to bus No. 12. The IEEE 33-bus test system is designed to feed the distributed linear and non-linear loads with a total power of 2.73 and 6.738 MVar,respectively.
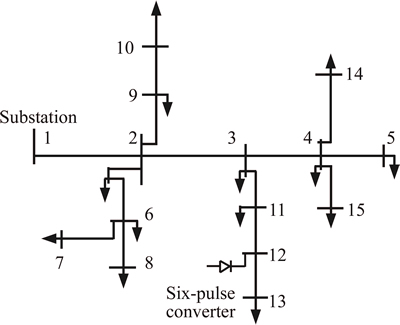
Fig. 4 15-bus IEEE test system
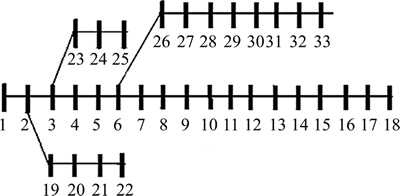
Fig. 5 33-bus IEEE test system
In IEEE 33-bus test system, the non-linear loads which distort system voltage and current waveforms are six-pulse rectifiers with active and reactive powers of 0.1 pu (1 MW) and 0.075 pu (0.75 MVar), respectively. These non-linear loads are in buses No. 5 and 26.Specification of IEEE 15-bus test systems, line data and load data are given in Tables 1 and 2 respectively.
Table 1 Line data in 15-bus test system
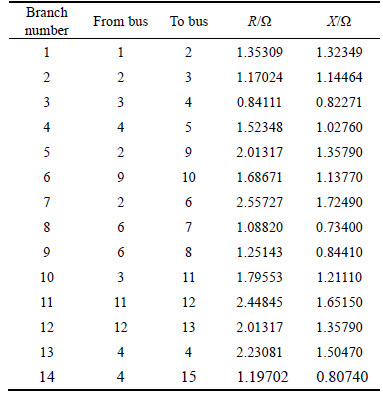
Table 2 Load data in 15-bus test system.
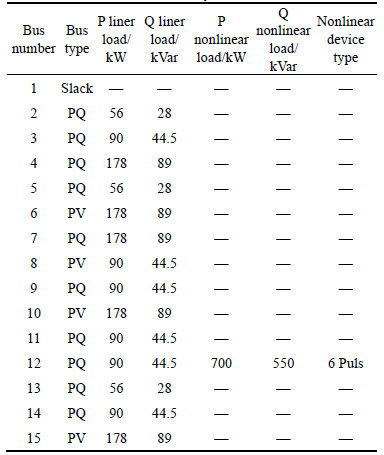
Using harmonic power-flow analysis before capacitor and active power conditioner allocation, the harmonic components including fundamental harmonic voltages, rms voltages and THD of voltages in all buses of 15-bus IEEE test system, are listed in Table 3.
Specification of IEEE 33-bus test systems, line data and load data are given in Tables 4 and 5 respectively.
Similar to before test system, using harmonic power-flow analysis without presence of capacitor and active power conditioner, the harmonic components including fundamental harmonic voltages, rms voltages and THD of voltages in all buses of 33-bus IEEE test system, are shown in Table 6.
Table 3 Simulation results for bus voltage and THD voltage before optimization in 15-bus IEEE test system
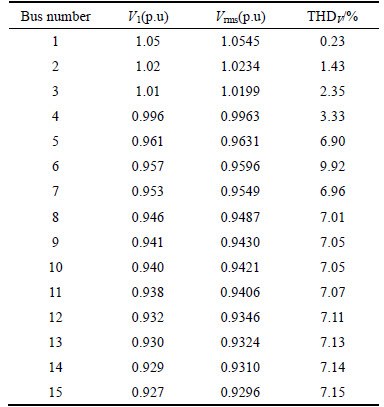
Table 4 Line data in 33-bus test system

Tables 7-11 compare four different cases which employ optimal capacitor and APC placement separately and simultaneously. The following cases are considered.
Case 1: Distribution system without APC and without shunt capacitor allocation (Base case).
Case 2: Only shunt capacitor allocation without APC allocation.
Table 5 Load data in 33-bus test system

Case 3: Only APC allocation without shunt capacitor allocation.
Case 4: Simultaneous APC and shunt capacitor allocation.
The simulation results in case 2 for 15-bus test system as listed in first row of Table 7, show that the power loss has been reduced to 202 kW (i.e. 12.38% compared to the initial condition of the network). Four capacitors (550, 450, 450 and 500 KVar) are used in the optimal case which are placed on buses 4, 8, 10 and 12, respectively. The results of capacitor placement for the 33-bus test system indicate that the power loss has been reduced to 340 kW (i.e. 12.38% compared to the initial condition of the network). Six capacitors (750, 550, 550, 450, 650 and 600 KVar) are used in the optimal case which are placed on buses 6, 13, 22, 25, 27 and 31, respectively. As listed in Table 8 the optimal APC allocation results show that three APCs (800, 700 and 500 KVar) are placed on buses 4, 9, and 13, respectively.
Table 6 Simulation results for bus voltage and THD voltage before optimization in 33-bus IEEE test system

Table 7 Results of only optimal capacitor allocation for systems (Case 2)
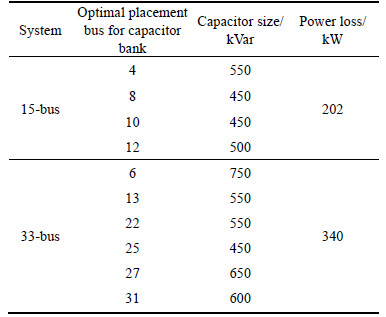
Table 8 Results of only optimal APC allocation for systems (Case 3)
.jpg)
Table 9 Results of optimal APC and capacitor banks simultaneously for systems (Case 4)

The power loss has been reduced to 196 kW for this case. The optimal results for 33-bus test show that the six APCs (800, 700, 500, 500, 800 and 600 KVar) are used in the optimal case in 33-bus system which are placed on buses 6, 8, 13, 23, 29 and 32, respectively. The power loss has been reduced to 287 kW for this case. In case 4, optimal active power conditioner and capacitor placement simultaneously lead to the most optimum network. The power loss of 15-bus system has been reduced to 128 kW and of 33-bus system has been reduced to 214 kW for this case. Employing APCs and capacitor banks simultaneously in a distribution system increases system efficiency, reduces THD index, reduces line losses, and improves system voltage profile.
Table 10 Comparison results for different cases using proposed method in 15-bus IEEE test system
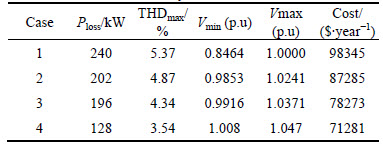
Table 11 Comparison results for different cases using proposed method in 33-bus IEEE test system

Figures 6 and 7 respectively show the THD index of all buses of test system under four case studies of 15-bus and 33-bus test systems. Simulation results showed that optimal allocation of APCs and capacitor banks simultaneously (case 4) reduces THD index.
Figure 8 shows the voltage profiles of 15-bus IEEE test system before and after optimal active power conditioner and capacitor placement. The voltage profile is obviously improved after the optimization.
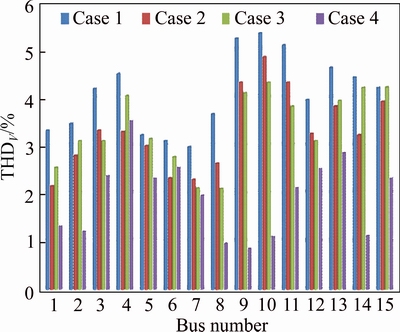
Fig. 6 THD analysis results of 15-bus IEEE test system
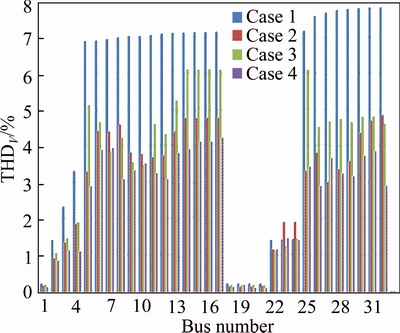
Fig. 7 THD analysis results of 33-bus IEEE test system
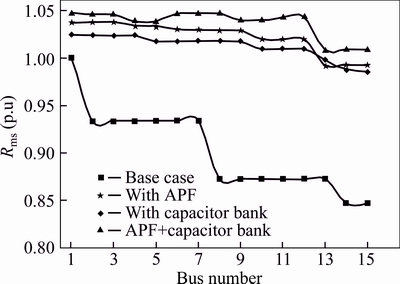
Fig. 8 Comparison of voltage profile in optimal APC and capacitor placement in 15-bus test system
Figure 9 shows the voltage profiles of 33-bus IEEE test system before and after optimal active power conditioner and capacitor placement. The voltage profile is obviously improved after the optimization. Figures10 and 11 show the active loss reduction of different cases of proposed method in 15-bus and 33-bus systems, respectively. Only capacitor bank placement, APC placement, employing APCs and capacitor banks simultaneously are considered different states. In Tables 10 and 11 the comparison of four ceases versus of power loss, total harmonic distortion index, the minimum voltage and the maximum voltage of obtained voltage profile and finally the economic comparison of different cases according to total cost of installed devices in network is presented. Also the comparison between the obtained results in case 2 (only shunt capacitor bank) using proposed method and Ref. [16] in 33-bus system has been presented in Table 11 to validate the proposed method.

Fig. 9 Comparison of voltage profile in optimal APC and capacitor placement in 33-bus test system

Fig. 10 Comparison of four case studies of proposed method for loss reduction in a 15-bus system
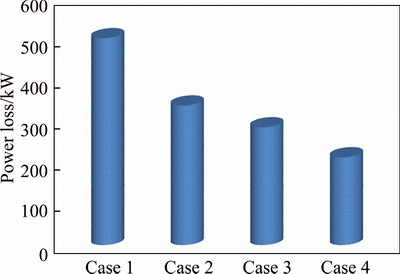
Fig. 11 Comparison of four case studies of proposed method for loss reduction in a 33-bus system
9 Conclusions
Distributed generation, passive harmonic filters, active filters, DFACTS devices and reconfiguration feeder network alter the impedance structure of the network, affecting the network harmonic distortion level. This mainly can affect and change the optimal location and size of shunt capacitor bank in a harmonic distorted system. Newly a custom power device which is recently employed in distribution system to improve power quality is APC. It is a shunt multi-function compensating device, which, depending on the available controller design, has the ability of voltage sag and harmonic distortion mitigation, performs power factor correction, and improves the overall power quality. This paper presents an optimization algorithm for improvement of power quality using simultaneous optimal placement and sizing of APC and shunt capacitor banks in radial distribution networks in the presence of voltage and current harmonics. A novel method is proposed for the discrete optimization problem of fixed shunt capacitor and APC placement and sizing in the presence of voltage and current harmonics using PSO method. The objective function includes the cost of power losses, energy losses and those of the capacitor banks and APCs. The simulation results verified that using simultaneous optimal placement and sizing of APC and shunt capacitor banks the power loss of system; the maximum THD index and annual cost deceased, to 50%, 45% and 63% respectively. Results show that the proposed method is suitable for optimal capacitor placement and sizing in the presence of voltage and current harmonic in distribution network.
References
[1] GALLAL Y, ISMAEL M, FAHMY A. Capacitor allocation and sizing for distribution system via fuzzy techniques [J]. Global Advanced Research Journal of Engineering, Technology and Innovation, 2013, 2(6): 173-180.
[2] de SOUZA B A, DO ALVES H N, FERREIRA H A. Micro-genetic algorithms and fuzzy logic applied to the optimal placement of capacitor banks in distribution networks [J]. IEEE Trans Power Syst, 2004, 19(2): 942-947.
[3] HUANG S J. An immune based optimization method to capacitor placement in a radial distribution system [J]. IEEE Trans Power Del, 2000, 15(2): 744-749.
[4] AURIZIO D, GRANELLI G P, MARANNINO P, MARIO M. Optimal capacitor placement using deterministic and genetic algorithms [J]. IEEE Trans Power Syst, 2000, 15(3): 1041-1046.
[5] SEGURA SILVIO, ROMERO RUBEN, RIDER M J. Efficient heuristic algorithm used for optimal capacitor placement in distribution system [J]. Int J Electr Power Energy Syst, 2010, 32(1): 71-78.
[6] ETEMADI A H, FOTUHI-FIRUZABAD M. Distribution system reliability enhancement using optimal capacitor placement [J]. IET Gener Transm Distrib, 2008, 2(5): 621-631.
[7] EAJAL A, EL-AREF HAWARY M. Optimal capacitor placement and sizing in unbalanced distribution systems with harmonics consideration using particle swarm optimization [J]. IEEE Trans Power Deliver, 2010, 25(3): 1734-1741.
[8] TENG J H, CHANG C Y. Backward/forward sweep-based harmonic analysis method for distribution systems [J]. IEEE Trans Power Deliver, 2007, 22(3): 1665-1672.
[9] BANAEI M R, HOSSEINI S H, KHANMOHAMADI S G B. Loss reduction of distribution system using APC [J]. Simulation Modelling Practice and Theory, 2005, 13: 169-178.
[10] FARAHANI V, VAHIDI B, ABYANEH H A. Reconfiguration and capacitor placement simultaneously for energy loss reduction based on an improved reconfiguration method [J]. IEEE Trans Power Syst, 2011, 2(5): 621-631.
[11] CHANG C F. Reconfiguration and capacitor placement for loss reduction of distribution systems by ant colony search algorithm [J]. IEEE Trans Power Syst, 2008, 23(4): 1747-1755.
[12] OLIVEIRA L, CARNEIRO S, de OLIVEIRA E, PEREIRA J, SILVA I, COSTAI J. Optimal reconfiguration and capacitor allocation in radial distribution systems for energy losses minimization [J]. Int J Electric Power Energy Syst, 2010, 32(8): 840-848.
[13] SAJJADI S M, HAGHIFAM M R, SALEHI J. Simultaneous placement of distributed generation and capacitors in distribution networks considering voltage stability index [J]. Int J Electr Power Energy Syst, 2013, 46: 366-375.
[14] SADIGHMANESH A, ZARE K, SABAHI M. Distributed generation unit and capacitor placement for multi objective optimization [J]. Int J Electr Commun Eng, 2012, 2(5): 615-620.
[15] JAIN N, SINGH S N, SRIVASTAVA S C. PSO based placement of multiple wind DGs and capacitors utilizing probabilistic load flow model [J]. Swarm and Evolutionary Computation, 2014, 19: 15-24.
[16] TAHER S A, KARIMIAN A, HASANI M. A new method for optimal location and sizing of capacitors in distorted distribution networks using PSO algorithm [J]. Simulation Modelling Practice and Theory, 2011, 19: 662-672.
[17] MOHKAMI V, HOOSHMAND R, KHODABAKHSHIAN A. Fuzzy optimal placement of capacitors in the presence of nonlinear loads in unbalanced distribution networks using BF-PSO algorithm [J]. Applied Soft Computing, 2011, 11: 3634-3642.
[18] TAHER S A, HASANI M, KARIMIAN A. A novel method for optimal capacitor placement and sizing in distribution systems with nonlinear loads and DG using GA [J]. Commun Nonlinear Sci Numer Simulat, 2011, 16: 851-862.
[19] ZIARI I, JALILIAN A. Optimal placement and sizing of multiple APLCs using a modified discrete PSO [J]. Int J Electric Power Energy Syst, 2012, 43: 630-639.
[20] FARHOODNEA M, MOHAMEDA A, SHAREEF H, ZAYANDEHROODI H. Optimum placement of active power conditioner in distribution systems using improved discrete firefly algorithm for power quality enhancement [J]. Applied Soft Computing, 2014, 23: 249-258.
[21] SAADAT H. Power system analysis [M]. 2nd ed. London: McGraw-Hill Higher Education, 2009.
[22] TENG J H, CHANG C Y. Backward/forward sweep-based harmonic analysis method for distribution systems [J]. IEEE Trans. Power Deliver, 2007, 22: 1665-1672.
[23] TENG J H. A network-topology-based three-phase load flow for distribution systems [J]. Proc Natl Sci Counc ROC (A), 2000, 24(4): 259-264.
[24] MOHAMMADI M. Bacterial foraging optimization and adaptive version for economically optimum sitting, sizing and harmonic tuning orders setting o LC harmonic passive power filters in radial distribution systems with linear and nonlinear loads [J]. Applied Soft Computing, 2015, 29: 345-356.
[25] Task force on harmonic modeling and simulation, modeling and simulation of the propagation of harmonics in electric power networks: Parts I and II [R]. IEEE Trans Power Deliv, 1996, 11(1): 435-474.
[26] RIBEIRO P F. Guidelines on distribution system and load representation for harmonic studies [C]// Proceedings of 5th International Conference on Harmonic in Power System, JCHPS. Atlanta, GA, USA: IEEE, 1992: 272-280.
[27] KENNEDY J, EBERHART R, SHI Yu-hui. Swarm intelligence [R]. San Francisco: Morgan Kaufmann Publishers, 2001.
[28] CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multi-dimensional complex space [J]. IEEE Trans Evolut Comput, 2002, 6(1): 58-73.
[29] IEEE recommended practices and requirements for harmonic control in electric power systems [R]. New York: IEEE Std, 1993: 519-1992.
[30] AMANIFAR O, GOLSHAN M E H. Optimal distributed generation placement and sizing for loss and THD reduction and voltage profile improvement in distribution systems using particle swarm optimization and sensitivity analysis [J]. International Journal on Technical and Physical Problems of Engineering, 2011, 7(3): 47-53.
[31] GOSWAMI S K, BASU S K. A new algorithm for the reconfiguration of distribution feeders for loss minimization [J]. IEEE Trans Power Del, 1992, 7(3): 1484-1491.
(Edited by YANG Hua)
Cite this article as: Mohammadi Mohammad. Particle swarm optimization algorithm for simultaneous optimal placement and sizing of shunt active power conditioner (APC) and shunt capacitor in harmonic distorted distribution system [J]. Journal of Central South University, 2017, 24(9): 2035–2048. DOI: https://doi.org/10.1007/s11771- 017-3613-7.
Received date: 2016-05-05; Accepted date: 2016-12-27
Corresponding author: Mohammadi Mohammad, PhD; Tel: +98-09188607414; E-mail: mohamadi.m@iaub.ac.ir

