型钢-钢管混凝土轴压柱核心混凝土应力-应变关系
肖阿林1,何益斌1,郭健1, 2
(1. 湖南大学 土木工程学院,湖南 长沙,410082;
2. 湖南大学 设计研究院,湖南 长沙,410082)
摘 要:对型钢-钢管混凝土轴压柱核心混凝土的受力特征进行分析;借鉴典型的约束混凝土本构关系,提出核心混凝土等效单轴受压应力-应变关系模型,该模型考虑了型钢翼缘对核心混凝土约束效应的贡献。利用所建立的核心混凝土应力-应变关系模型,采用数值方法对型钢-钢管混凝土轴压组合柱的荷载-变形关系进行分析。研究结果表明:核心混凝土内部存在双重约束区域,其力学性能与钢管混凝土柱中的核心混凝土存在差异;数值计算结果与试验结果较吻合,表明所提出的核心混凝土应力-应变关系模型能较准确地描述型钢-钢管混凝土轴压柱的受力过程、变形特征和承载能力等基本力学性能。
关键词:组合柱;核心混凝土;应力;应变;受力特征;数值分析
中图分类号:TU398.9 文献标志码:A 文章编号:1672-7207(2010)01-0341-06
Stress-strain relation of core concrete of aixally-loaded steel tubular columns filled with steel-reinforced concrete
XIAO A-lin1, HE Yi-bin1, GUO Jian1, 2
(1. School of Civil Engineering, Hunan University, Changsha 410082, China;
2. Institute of Design and Research for Architecture and Structure, Hunan University, Changsha 410082, China)
Abstract: The working mechanism and stress characters of core concrete of aixally-loaded steel tubular columns filled with steel-reinforced concrete were investigated. Based on the typical constitutive models of confined concrete, stress-strain relationship describing the equivalent single-axis compressive stress of the core concrete was put forward by considering the confining contribution of steel flanges. Moreover, full-range load-deformation relationship for the composite columns under axial load was calculated by using the proposed constitutive relationship. The results show that the mechanics performance of the core concrete is different from that of concrete-filled steel tubular column, due to the inner double confined area of core concrete of the composite columns. The calculated results and the experimental ones are in agreement well, which shows the proposed stress-strain relationship of core concrete is feasible in the evaluation of ultimate strength and deformation of aixally-loaded steel tubular columns filled with steel-reinforced concrete.
Key words: composite column; core concrete; stress; strain; mechanics characteristic; numerical analysis
型钢-钢管混凝土柱是一种先将型钢插入钢管后浇筑混凝土的新型复式组合柱。与钢管混凝土柱相比,它可以解决重载柱中厚壁钢管成型困难的问题,且具有更好的抗火性能;与型钢混凝土柱相比,它不需要绑扎钢筋和支模等繁琐工序,且由于混凝土受到钢管的约束使得其抗震性能明显比型钢混凝土柱的抗震性能更优[1-2],因此,这种组合柱在高层建筑及桥梁结构的重载柱中具有广阔的应用前景。工程材料的本构关系反映受力全过程中材料力和变形关系,是材料内部微观机理的宏观行为表现,是结构强度和变形计算中必不可少的依据。目前,国内外针对钢管约束核心混凝土应力-应变关系进行了大量的研究,并取得了一定成果[3-8]。然而,尚未发现有专门针对型钢-钢管混凝土组合柱核心混凝土应力-应变关系的研究报道。因此,建立简便、明确、准确度较高的核心混凝土应力-应变关系模型,对于深入认识型钢-钢管混凝土组合柱的力学性能和受力机理具有重要的意义。为此,本文作者在参考分析国内外应用较广、影响较大、典型的约束混凝土应力-应变关系模型的基础上,结合型钢-钢管混凝土组合柱核心混凝土的受力特征,考虑型钢翼缘对核心混凝土约束效应的贡献,提出核心混凝土极限应力、极限应变的计算方法和约束混凝土应力-应变关系模型。在此基础上,将其应用于数值计算中。
1 核心混凝土的受力特征
型钢-钢管混凝土中的钢管与约束混凝土结构中钢管、螺旋(圆形)箍筋和焊接网片等众多横向配筋构造一样,其主要作用是约束其内部混凝土的横向变形,使混凝土处于三轴受压状态,提高混凝土的强度和变形能力,改善受压构件或结构中受压部分的力学性能。与钢管混凝土类似,型钢-钢管混凝土中核心混凝土的强度和变形能力的提高程度,主要与所受侧向约束应力有关。与钢管混凝土不同的是,除了外围钢管对核心混凝土提供侧向约束以外,核心型钢翼缘对其内部区域混凝土也存在一定的约束效应[2]。因此,型钢-钢管混凝土轴压柱中核心混凝土存在一个约束区和一个双重约束区(如图1所示),故其力学性能与钢管混凝土柱中的核心混凝土力学性能有区别。
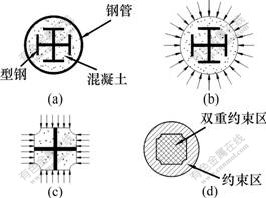
(a) 截面形式;(b) 钢管的约束效应;(c) 型钢翼缘的约束效应;(d) 约束机理
图1 组合柱核心混凝土约束机理
Fig.1 Confining mechanism of steel tube and structural steel to core concrete
2 应力-应变关系模型
2.1 模型的建立
虽然型钢-钢管混凝土轴压柱中核心混凝土的力学性能与钢管混凝土柱中的核心混凝土的力学性能不尽相同,但仍可通过修正既有钢管混凝土柱核心混凝土的应力-应变关系模型对其进行近似描述。目前,国内外学者通过试验回归或理论分析等方法,提出了10多种钢管约束混凝土的应力-应变关系模型[3-8]。其中,精度相对较高、应用较广泛、影响较大的圆钢管约束混凝土本构模型主要有韩林海等[4-8]提出的模型。据文献[9-11],并结合型钢-钢管混凝土组合柱核心混凝土的受力特征,本文建立基于Saenz模型的型钢-钢管混凝土柱核心混凝土受压应力-应变关系模型(如图2所示):
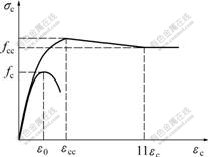
图2 核心混凝土的应力-应变模型
Fig.2 Stress-strain model of core concrete
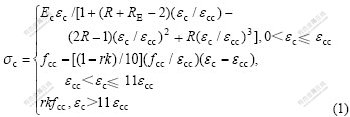
式中:σc和εc分别为核心混凝土的压应力和压应变;fcc为约束混凝土的抗压强度;εcc为fcc所对应的混凝土压应变;Ec为核心混凝土的初始弹性模量;R,RE,r和k均为待定参数[9]。
2.2 fcc和εcc等有关参数的确定
Mander等[12]提出的约束混凝土的抗压强度和极限压应变模型为:
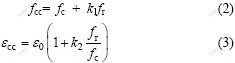
其中:fc和ε0分别为未受约束混凝土的轴心抗压强度及其所对应的压应变;fr为由于钢管壁的环箍作用核心混凝土所受到的径向约束应力。据文献[12]和有关试验结果,考虑到型钢-钢管混凝土柱中型钢翼缘对混凝土的约束影响,参数k1和k2分别按下式计算:k1= 3.3+ρ,k2=16.5+ρ,其中:ρ表示型钢-钢管混凝土柱的配骨指标。型钢翼缘对核心混凝土的约束效应应当采用型钢翼缘的约束刚度加以表述,在此,用配骨指标ρ粗略地表征型钢翼缘对核心混凝土的约束贡献。
采用式(2)和(3)计算fcc和εcc时需要确定钢管屈服时钢管壁环向应力,以求得等效侧向约束应力fr。在组合柱达到极限承载力时,钢管壁处于纵向受压、环向受拉和径向受压的多轴应力状态。要精确地确定钢管的环向应力非常困难。研究表明,极限状态时核心混凝土受到的径向约束应力与钢管的径厚比(D/t)(其中D为钢管外径,t为钢管壁厚)及钢管的屈服强度(fyt)关系密切[11]。在此,本文采用有关文献的推荐公式计算核心混凝土受到的径向约束应力fr[11]:

根据文献[13],核心混凝土的初始弹性模量Ec可由下式计算:
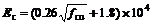 (5)
(5)
其中:fcu为混凝土立方体抗压强度。根据文献[9, 11],
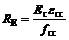 (6)
(6)
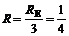 (7)
(7)
混凝土强度影响参数r按下式计算[14]:
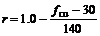 , 30≤fcu≤100 (8)
, 30≤fcu≤100 (8)
研究表明[11],峰值应力后线性下降段的斜率k主要取决于钢管的径厚比(D/t)。本文据文献[11]中的推荐公式计算k:
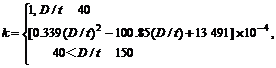 (9)
(9)
3 模型验证
为了检验上述核心混凝土应力-应变关系模型的合理性,下面采用上述模型通过数值方法对型钢-钢管混凝土轴压柱进行荷载-变形全过程分析。
3.1 钢材应力-应变关系模型的确定
首先必须确定钢材(钢管及型钢)和核心混凝土的应力-应变关系模型,本文将选取前面建立的核心混凝土应力-应变关系模型。下面介绍所采用钢管及型钢的应力-应变关系模型。
在型钢-钢管混凝土柱中,钢管和型钢的受力状态有所不同,因此,应分别采用不同的应力-应变关系模型。对于钢管,考虑其处于环向和轴向受力状态,采用两阶段的理想弹塑性模型(见图3(a));对于型钢,由于作用在型钢上的侧向力较小,可以认为型钢仅承受轴向荷载作用,同时,外围钢管和混凝土的存在有效地防止了型钢的局部屈曲。因此,型钢的应力-应变关系采用二次塑流模型(见图3(b))。钢管及型钢的应力-应变关系表达式见文献[4, 15]。
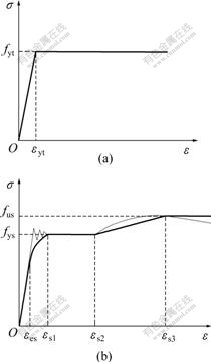
fus为型钢的抗拉强度;fys为型钢的屈服强度;fyt为钢管屈服强度;εes为比例极限应变;εs1为型钢屈服应变;εs2为型钢强化段初始应变;εs3为型钢抗拉强度应变
(a) 钢管的应力-应变模型;(b) 型钢的应力-应变模型
图3 钢管和型钢的应力-应变关系模型
Fig.3 Stress-strain model of steel tube and structural steel
3.2 数值计算模型的建立
在确定了钢材及核心混凝土的应力-应变关系模型基础上,利用数值分析方法,可计算出型钢-钢管混凝土轴压柱的荷载-变形全过程关系曲线。计算时采用如下假设:
(1) 钢与混凝土之间无黏结滑移,构件在变形过程中始终保持为平截面。
(2) 钢管及型钢的纵向应力-应变关系按文献[4]提供的模型进行计算,核心混凝土纵向应力-应变关系按式(1)确定。
(3) 对于轴压长柱试件,假定构件的挠曲线为正弦半波曲线,且考虑构件存在1/1 000柱长的初始挠度。
基于上述假设,型钢-钢管混凝土在受力过程中应符合如下条件。
(1) 内、外力平衡条件:
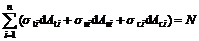 (10)
(10)
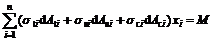 (11)
(11)
(2) 变形协调条件:
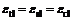 (12)
(12)
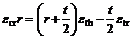 (13)
(13)
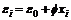 (14)
(14)
式中:n为截面的条带单元数;σti,σsi和σci分别为第i个单元中钢管、型钢和混凝土的轴向应力;Ati,Asi和Aci分别为第i个单元中钢管、型钢及混凝土所对应的面积;xi为第i个单元距截面形心轴的距离;N和M分别为外力和外弯矩;εtl,εsl和εcl分别为截面钢管、型钢及混凝土的轴向应变;εcr为混凝土径向应变;εth和εtr分别为钢管环向和径向应变;r和t分别为钢管的内半径和壁厚;εi和ε0分别为第i单元条带中心处的应变和截面形心处的应变;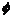 为截面曲率。
为截面曲率。
在进行荷载-变形关系计算时,首先将构件跨中截面分为若干个单元条带,然后,利用内外力平衡条件和变形协调条件通过迭代方法求解各级变形下构件所对应的荷载,依此类推,可计算出型钢-钢管混凝土轴压柱的荷载-变形关系曲线。有关纤维模型法的具体计算方法及相关步骤见文献[4,15]。
3.3 数值计算结果与试验结果的比较
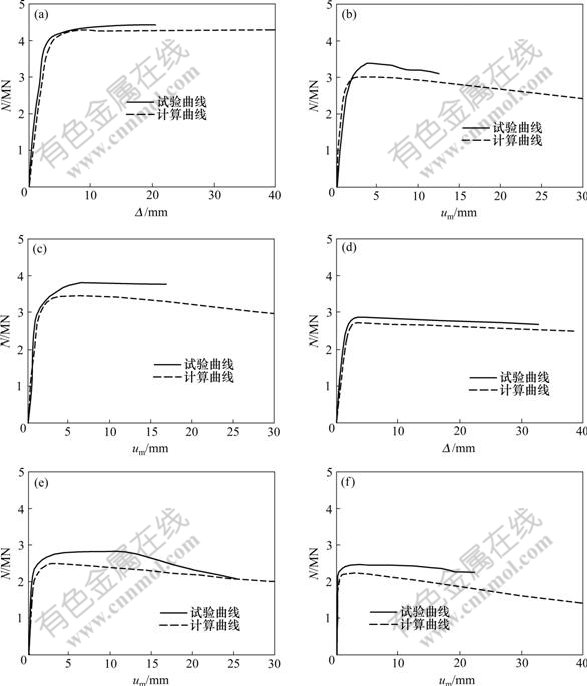
依据上述方法编制非线性分析程序,并通过试验对程序进行验证。表1所示为本文及文献[1]试验试件的详细参数和试验结果;图4所示为部分试件计算曲线与试验曲线的对比情况,其中:实线为试验结果;虚线为数值计算结果;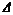 为轴向变形;um为柱中侧向挠度。由图4可以看出:计算曲线与试验曲线基本吻合,说明本文提出的核心混凝土本构模型可以较好地描述型钢-钢管混凝土轴压柱的荷载-变形关系;此外,轴压长柱计算结果吻合程度比短柱的吻合程度稍差。图5所示为对数值计算得到的轴压构件极限承载力(Nuc)和试验结果(Nue)的对比。同时,表1列出了不同试件二者的比值(Nuc/Nue), 其平均值为0.928,标准差为0.041,说明计算结果略低于试验值,偏于安全。
为轴向变形;um为柱中侧向挠度。由图4可以看出:计算曲线与试验曲线基本吻合,说明本文提出的核心混凝土本构模型可以较好地描述型钢-钢管混凝土轴压柱的荷载-变形关系;此外,轴压长柱计算结果吻合程度比短柱的吻合程度稍差。图5所示为对数值计算得到的轴压构件极限承载力(Nuc)和试验结果(Nue)的对比。同时,表1列出了不同试件二者的比值(Nuc/Nue), 其平均值为0.928,标准差为0.041,说明计算结果略低于试验值,偏于安全。
表1 试件试验参数及试验结果
Table 1 Experimental parameters and results
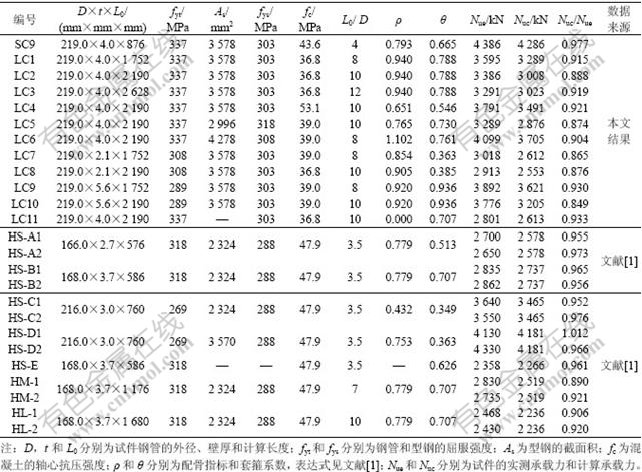
(a) 试件SC9; (b) 试件LC2; (c)试件LC10; (d) 试件HS-B; (e) 试件HM; (f) 试件HL
图4 试件承载力数值计算结果与试验结果的比较
Fig.4 Comparisons between calculation results and experimental results of specimens
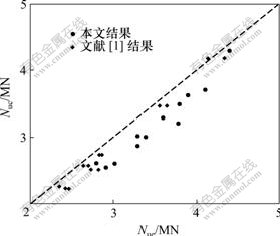
图5 轴压试件承载力计算值与试验值比较
Fig.5 Comparison of calculated strength and its test results
4 结论
(1) 对型钢-钢管混凝土轴压柱核心混凝土的受力特征进行了分析,提出型钢-钢管混凝土轴压柱中核心混凝土存在一个约束区和一个双重约束区,故其力学性能与钢管混凝土柱中的核心混凝土有所区别。
(2) 在综合比较国内外典型模型的基础上,结合型钢-钢管混凝土组合柱核心混凝土的受力特征,考虑型钢翼缘对核心混凝土约束效应的贡献,提出了核心混凝土等效单轴受压应力-应变关系模型。
(3) 利用所建立的核心混凝土应力-应变关系模型,采用数值方法对型钢-钢管混凝土轴压组合柱的荷载-变形关系进行了全过程分析,数值计算结果与试验结果较吻合,表明所提出的核心混凝土应力-应变关系模型和所采用的数值计算方法能较准确地描述型钢-钢管混凝土轴压柱的受力过程、变形特征和承载能力等基本力学性能。
参考文献:
[1] 王清湘, 赵大洲, 关萍. 钢骨-钢管高强混凝土轴压组合柱受力性能的试验研究[J]. 建筑结构学报, 2003, 24(6): 45-49.
WANG Qing-xiang, ZHAO Da-zhou, GUAN Ping. Study on the mechanical properties of axially loaded steel tubular columns filled with steel-reinforced high-strength concrete[J]. Journal of Building Structures, 2003, 24(6): 44-49.
[2] HE Yi-bin, XIAO A-lin. Limit analysis of steel tubular columns filled with structural steel[C]//Proceedings of the 8th International Conference on Steel-Con Crete Composite and Hybrid Structures (Special Issue of Steel Construction). Harbin, China, 2006: 544-550.
[3] 钟善桐. 钢管混凝土结构[M]. 北京: 清华大学出版社, 2003: 11.
ZHONG Shan-tong. The concrete-filled steel tubular structures[M]. Beijing: Tsinghua University Press, 2003: 11.
[4] 韩林海. 钢管混凝土结构: 理论与实践[M]. 北京: 科学出版社, 2004: 64-68.
HAN Lin-hai. Concrete filled steel tubular structures: From theory to practice[M]. Beijing: Science Press, 2004: 64-68.
[5] Sakino K, Hayashi H. Behavior of concrete filled steel tubular stub columns under concentric loading[C]//Proceedings of the Third International Conference on Steel-Concrete Composite Structure. Fukuoka, Japan, 1991: 25-30.
[6] Saenz L P. Discussion of ‘Equation for the stress–strain curve of concrete’ by P. Desayi, and S. Krishnan[J]. Journal of the American Concrete Institute, 1964, 61(7): 1229-1235.
[7] Scott, Park R, Priestly N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. American Concrete Institute Structure Journal, 1982, 79(1): 13-27.
[8] Ottosen N S. Constitutive model for short-time loading of concrete[J]. Journal of Structural Engineering, ASCE, 1979, 105(1): 127-141.
[9] Hu H T, Huang C S, Chen Z L. Finite element analysis of CFT columns subjected to an axial compressive force and bending moment in combination[J]. Journal of Constructional Steel Research, 2005, 61(5): 1692-1712.
[10] Ellobody E, Young B, Lam D. Behaviour of normal and high strength concrete-filled compact steel tube circular stub columns[J]. Journal of Constructional Steel Research, 2006, 62(11): 706-715.
[11] Hu H T, Huang C S, Wu M H, et al. Nonlinear analysis of axially loaded concrete-filled tube columns with confinement effect[J]. Journal of Structural Engineering, ASCE, 2003, 129(10): 1322-1329.
[12] Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, ASCE, 1988, 114(8): 1804-1826.
[13] 陈肇元, 朱金铨, 吴佩刚. 高强混凝土及其应用[M]. 北京: 清华大学出版社, 1992: 78-79.
CHENG Zhao-yuan, ZHU Jin-quan, WU Pei-gang. High-strength concrete and application[M]. Beijing: Tsinghua University Press, 1992: 78-79.
[14] Giakoumelis G, Lam D. Axial capacity of circular concrete-filled tube columns[J]. Journal of Constructional Steel Research, 2004, 60(7): 1049-1068.
[15] 肖阿林. 钢骨-钢管高性能混凝土轴压组合柱受力性能与设计方法研究[D]. 长沙: 湖南大学土木工程学院, 2009: 92-102.
XIAO A-lin. Research on behavior and design method of steel-reinforced high-performance concrete filled steel tubular columns under axial load[D]. Changsha: School of Civil Engineering, Hunan University, 2009: 92-102.
收稿日期:2009-04-10;修回日期:2009-07-02
基金项目:湖南省科技计划项目(2008GK312);湖南省杰出青年基金资助项目(05JJ10009)
通信作者:肖阿林(1980-),男,湖南宁乡人,博士,从事混凝土结构及组合结构研究;电话:13787049306;E-mail: xiaoalin1980@163.com
(编辑 陈灿华)