Microstructure formation and grain refinement of Mg-based alloys by electromagnetic vibration technique
来源期刊:中国有色金属学报(英文版)2010年第7期
论文作者:M. J. LI T. TAMURA N. OMURA K. MIWA
文章页码:1192 - 1198
Key words:magnesium alloy; electromagnetic vibration; microstructure formation; grain refinement; solidification
Abstract: The microstructure formation and grains refinement of two Mg-based alloys, i.e. AZ31 and AZ91D, were reported using an electromagnetic vibration (EMV) technique. These two alloys were solidified at various vibration frequencies and the microstructures were observed. The average size of grains was quantitatively measured as a function of vibration frequencies. Moreover, the grain size distribution was outlined versus number fraction. A novel model was proposed to account for the microstructure formation and grain refinement when considering the significant difference of the electrical resistivity properties of the solid and the liquid during EMV processing in the semisolid state. The remarkable difference originates uncoupled movement between the mobile solid and the sluggish liquid, which can activate melt flow. The microstructure evolution can be well explained when the fluid flow intensity versus vibration frequency is taken into account. Moreover, the influence of the static magnetic field on texture formation is also considered, which plays an important role at higher vibration frequencies.

M. J. LI, T. TAMURA, N. OMURA, K. MIWA
National Institute of Advanced Industrial Science and Technology,
Materials Research Institute for Sustainable Development, Nagoya 463-8560, Japan
Received 23 September 2009; accepted 30 January 2010
Abstract: The microstructure formation and grains refinement of two Mg-based alloys, i.e. AZ31 and AZ91D, were reported using an electromagnetic vibration (EMV) technique. These two alloys were solidified at various vibration frequencies and the microstructures were observed. The average size of grains was quantitatively measured as a function of vibration frequencies. Moreover, the grain size distribution was outlined versus number fraction. A novel model was proposed to account for the microstructure formation and grain refinement when considering the significant difference of the electrical resistivity properties of the solid and the liquid during EMV processing in the semisolid state. The remarkable difference originates uncoupled movement between the mobile solid and the sluggish liquid, which can activate melt flow. The microstructure evolution can be well explained when the fluid flow intensity versus vibration frequency is taken into account. Moreover, the influence of the static magnetic field on texture formation is also considered, which plays an important role at higher vibration frequencies.
Key words: magnesium alloy; electromagnetic vibration; microstructure formation; grain refinement; solidification
1 Introduction
Because of the eco-friendly characteristic of the magnesium based alloys, much interest has been attracted from the viewpoint of strategy in making the research and development roadmap in past decades. However, in addition to the poor corrosion resistance, the unsatisfactory mechanical property of the alloy system is another great constraint for engineering application, in particular when they are used as structural components. Hence, in order to widen the applicability of the alloys, more work is required to improve the mechanical properties. According to Hall-Petch relation, the finer the grain size of an alloy is, the higher the strength of the alloy will be. Therefore, to achieve a grain-refined microstructure is an effective approach in enhancing the performance of the alloy.
Several techniques have been developed for the production of refined structures in a solidified ingot, among which particle incubation has been successfully applied in Al-based alloys[1] and ironmaking and steelmaking industry. However, for the magnesium-based alloys, the externally added particle may deteriorate the alloy recyclability property that is one of the most important merits for the metallic system.
Without adding any incubation agent but imposing electromagnetic vibration (EMV) force, VIVES[2] obtained refined microstructures in a series of Al-based alloys. Here, it is supplemented that the generation of EMV force is simply based on the Fleming left hand rule, which requires a perpendicular relation between the direction of magnetic field and that of flowing electric current. Following this pioneering work, MIWA and co-workers[3-6] solidified a number of alloy systems using the EMV technique and examined the microstructure evolution, more often than not, as a function of vibration frequency. They found that microstructures of all materials investigated had a minimum average grain size at certain frequency bands, and lower or higher frequencies would result in relative coarse structures. DOND et al[7] and ASAI[8] were another two groups who used the technique to investigate the solidification behavior of various alloys.
In this work, we solidified AZ31 and AZ91D magnesium alloys in a superconductor-based static magnet field at the magnetic flux density of B0=10 T when an alternating current of 60 A flew through the alloys. The microstructure formation in these two alloys was examined as a function of vibration frequency, f, and the grains refinement mechanism was investigated when considering the vibration characteristic in the semi-solid mushy zone.
2 Experimental
Commercial AZ31 and AZ91D ingots were cleaned and then remelted, respectively, in an electric furnace under the protection of a gas mixture with a proportion of less than 2% of SF6 and balanced by CO2. The molten alloys were kept approximately 50 K above their liquidus, i.e., 953 K for AZ31 and 921 K for AZ91D to homogenize the chemical composition; and then poured into a pre-heated metallic mold to cast a rod. The rod was then machined into a short bar with the specification of 6 mm in diameter and then encapsulated in an alumina tube. At two extremes of the specimen, two carbon blocks were used to fix the sample. These two carbon blocks were connected with copper electrodes, by which the alternating current could flow through the specimen. More detailed description on the sample setup has been given elsewhere[9-10].
The as-set sample kit was placed into a superconducting magnetic bore, in which a static magnetic field could be generated with a magnetic flux density up to 10 T. An arc-shaped graphite heater was used to cover onto the alumina tube in the sample area. Thus, the sample could be heated to be melted. A thermocouple was embedded into an as-made hole in the alumina tube to monitor the sample thermal profile, which was important for the determination of the EMV timing moment during cooling. Both kinds of samples were heated and melted and then kept at the overheated temperature for about 120 s to homogenize the composition. And then, the graphite heater was pulled up to cool the sample naturally. When the sample temperature reached 953 K for AZ31 and 898 K for AZ91D alloys, the alternating current was switched on to vibrate the sample till a well-set temperature and then cooling water with a flow rate of 6 L/min was sprayed onto the alumina tube to quench the sample.
When a sample was solidified, it was sectioned along the diametric direction with the cutting plane being perpendicular to the direction of the magnetic field. The sample was then mounted, ground, and polished following the metallographic preparation procedure. The specimen was then etched and the microstructures were observed. To quantify the microstructure development as a function of vibration frequency, the average diameters of grains were measured using the centroidal method, i.e. the mean length of the grain was obtained at two degree intervals when passing through the grains centroid.
Moreover, the electron backscattering diffraction (EBSD) technique was employed on the basis of a scanning electron microscope. Here, it should be noted that, because Mg alloys are active to react with moisture and easy to be oxidized in air, attention was paid during sample preparation. The small atomic number of the Mg alloy generates low diffraction intensity during data acquisition. Therefore, in order to produce a clear Kikuchi pattern for identification, the sample was first polished and then etched using an ion beam shower system to remove the deformed layer. This operation was very important and essential for Mg alloys. The sample was set into the SEM chamber immediately as soon as ion beam etching was completed. During data acquisition, one-step scanning generated a single Kikuchi pattern which corresponded to an indexing pixel and was represented as one pixel in the EBSD pattern in the data analysis. The EBSD color map was produced using the image quality as gray scale and inverse pole figure to decode the color pixels.
3 Results
3.1 Qualitative results of AZ31 and AZ91D alloys
In Figs.1(a)-(d), four microstructures of the AZ31 alloys are depicted, which are solidified at the frequencies of 50, 500, 1 000, and 5 000 Hz, respectively. One can find that at the low frequency of 50 Hz and the high frequency of 5 000 Hz, the microstructures are coarse with rosette-like dendrites. When the vibration is operated at medium frequency, e.g. f=500 Hz and f= 1 000 Hz, the microstructures become rather fine and consist of almost equiaxed grains in Figs.1(b) and (c).
In Figs.1(e)-(h), four microstructures of the AZ91D alloys are shown, which are solidified at the frequencies of 50, 900, 2 000 and 5 000 Hz, respectively. Similar to those in the AZ31 alloy, the microstructures are rather coarse with independent equiaxed dendrites at f=50 Hz and f=5 000 Hz. When the alloy is vibrated at the frequency of f =900 Hz, the equiaxed grains characterize the microstructure. With the increase of vibration frequency to f =2 000 Hz, the number of equiaxed grains becomes rare and instead that of the equiaxed dendrites, though some of them are immature, predominates, and the overall structure exhibits a ripened feature, as shown in Fig.1(g).
3.2 Quantitative results of AZ31 and AZ91D alloys
In addition to the qualitative observation, the average grain size of these optical microstructures can be quantified. Fig.2 indicates the quantitative relation of average grain size versus vibration frequency for these two alloys. One can see that the quantitative relation curves exhibit good coincidence with the qualitative

Fig.1 Microstructures of AZ31 alloy (a-d) and AZ91D alloy (e-h) (B0=10 T, I=50 A) solidified at different vibration frequencies: (a) f=50 Hz; (b) f=500 Hz; (c) f=1 000 Hz; (d) f=5 000 Hz; (e) f=50 Hz; (f) f=900 Hz; (g) f=2 000 Hz; (h) f=5 000 Hz
Observation, i.e. the average grain sizes are rather large at low frequencies and decrease with the increase of frequencies and eventually to the minimum of about 53 μm for AZ31 and 57 μm for AZ91D alloys. A further increase of frequency leads to the increase of grain size to about 110 μm for both alloys at f=5 000 Hz. Although these alloys experience a similar transition tendency as a function of frequency, a detectable difference in Fig.2 is

Fig.2 Measured average gain size as function of vibration frequency for AZ31 and AZ91D alloys
that the average grain size of the AZ91D alloy is larger that that of the AZ31 alloy at the same vibration frequency. In addition to the difference in chemical compositions that may induce some difference in chemical and physical properties relating to refinement, one of the probable reasons lies in the fact that the freezing interval of the AZ91D alloy covers approximately 133 K whereas that of AZ31 alloy spans about 65 K, enabling the AZ91D alloy to have a longer ripening time than AZ31, and thus producing a comparatively coarse structure. Moreover, it should be supplemented that we actually solidified the AZ31 alloy at eight different vibration frequencies and the AZ91D alloy at nine frequencies, as marked in Fig.2. For simplicity, we only depicted four typical microstructures for each alloy in Fig.1.
The average grain size gives an overall impression of a structure. However, one can see that an optical microstructure is, more often than not, hybrid rather than absolutely uniform. Therefore, to evaluate the quotient of grains with different average diameters, we counted the number of grains within a certain size interval and then the number fraction corresponding to the grain size interval could be determined. Fig.3 shows eight histograms of grain number fraction as a function of average diameter of grain size for AZ31 and AZ91D, in which the solidification condition of each specimen corresponds exactly to that in Fig.1 for these two alloys. For the AZ31 alloys solidified at f=50 Hz and f=5 000 Hz in Figs.3(a) and (d), there are some number fractions for the grains with a large average diameter, e.g. more than 140 μm, while at the small average diameter region, the number fractions in these two histograms are relatively higher than those obtained with large grain size, indicating the structures yielded at these two conditions are highly hybrid with a large scattering tendency. At the medium frequency interval from f=500 Hz to f=1 000 Hz, however, one can see that more than 90% grains fall into the range from about 40 μm to less than 80 μm in average diameter, in which about 50% grains are around 60 μm, as shown in Figs.3(b) and (c). This indicates that the grains have a narrow scattering band in diameter distribution for the AZ31 alloy.
In terms of the variation of grain number fraction versus grain size of the AZ91D alloy, one can find that it undergoes a similar evolution process as a function of vibration frequency, as indicated by the four histograms of Figs.3(e)-(h). At the low frequency of 50 Hz, the number fraction with large grain size shares a large quotient; while at the medium frequency of 900 Hz, grains fall into a narrow region, in which about 90% grains have the average diameter in the range from around 40 μm to less than 80 μm. When the vibration frequency increases, the number fractions of grains with large average diameter once again increase and accordingly those of refined grains decrease. It is worth noting that grains with the average diameter larger than 200 μm have a proportion of about 10% at the maximum frequency of 5 000 Hz, as shown in Fig.3(h).
4 Discussion
Grain refinement is a great concern in metallurgy. With regards to the refinement mechanism during EMV processing, cavitation was one of the predominant mechanisms over past decades, which was originated from the cavitation phenomenon occurring in ultrasonics[11]. As more experimental evidence is required to enable the mechanism viable, here we propose another model to interpret microstructure development as a function of vibration frequency.
The grain refinement during EMV processing mainly takes place in a mushy zone where solid and liquid co-exist. Here, it is assumed that if the solid and the liquid are driven to displace in a synchronic manner, there would be no interactions between the solid and the liquid and thus the resultant microstructure should be similar to that formed at normal casting because of the similar condition for the solute redistribution boundary layer. However, there is a huge difference in electric resistivities between the pure Mg and Al liquids and their solid counterparts at the same melting temperature[12-13], as shown in Table 1, in which the electric resistivity value of the liquid is about twice that of the solid. As the electric resistivity of the Mg-based
Table 1 Electric resistivities of solid and liquid of pure Mg and Al at their melting points[12-13] (n??m)

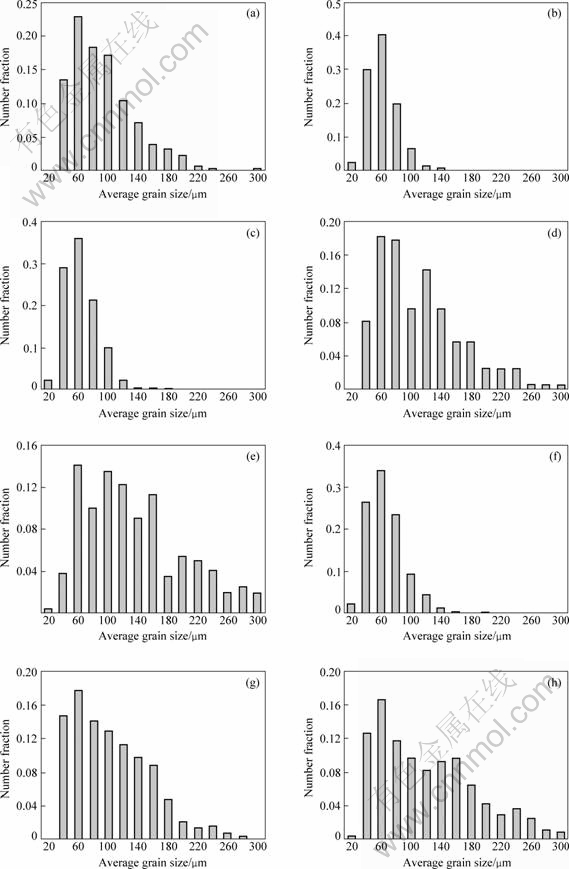
Fig.3 Histograms of AZ31 alloy (a-d) and AZ91D alloy (e-h) showing grain number fraction versus grain size: (a) f=50 Hz; (b) f=500 Hz; (c) f=1 000 Hz; (d) f=5 000 Hz; (e) f=50 Hz; (f) f=900 Hz; (g) f=2 000 Hz, (h) f=5 000 Hz
alloys, e.g. AZ31 and AZ91D, is more or less proportional to the amount of solute added[12], the overall electric resistivity of the liquid is estimated to be about twice that of the solid in the mushy zone, and thus the electrical resistance of the liquid is about twice that of the solid. Because the solid and the liquid in the mushy zone are more probably to be a parallel circuit, the electric current in the solid is about twice that in the liquid according to the Ohm’s law. Hence, according to the Newton’s second law of motion and electromagnetic theory, the Lorentz force induced upon the solid is about twice that on the liquid. Considering that there is little difference in density for the solid and the liquid in the mushy zone, the solid is driven to move with a larger acceleration and a higher velocity, and thus resulting in a longer displacement in comparison with that of the liquid within a half vibration cycle, as schematically depicted in Fig.4, which have been quantified elsewhere in detail[9].
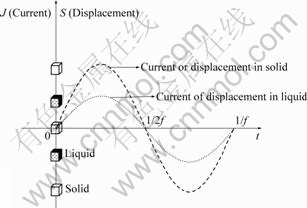
Fig.4 Schematic diagram to show difference of electric current and displacement between mobile solid and sluggish liquid within one vibration cycle
According to this deduction, it is readily to conclude that uncoupled motion takes place between the mobile solid and the surrounding sluggish liquid. As the mushy zone is confined within an alumina tube rather than in free space, such kind of uncoupled displacement can lead to melt flow during EMV processing. From the viewpoint of experiment, the effect of melt flow on grain refinement has been confirmed in many reports[14], in which dendrite fragmentation is considered to play the vital role though the detailed mechanism has not been well understood[15].
Based on several assumptions, the relative displacement of the leading solid was calculated as a function of vibration frequency[10], which spans about 60 mm at f=50 Hz. As the diameter of the Al2O3 tube is only 6 mm, the theoretical time duration for movement is about Dt=6/(60×2f)=0.001 s within a half cycle, i.e. that is only 10% of the half cycle interval of 0.01 s. This indicates that at this vibration frequency the total moving time for a solid particle is rather short while the dormant time is quite long. In this case, insufficient melt flow may be activated and thus the microstructure is rather coarse for both AZ31 and AZ91D alloys at f=50 Hz.
With the increase of vibration frequency, the relative leading displacement decreases and the dormant time correspondingly decreases, which may result in vigorous fluid flow in the semisolid state. The severe melt flow originates the grain multiplication and thus refined structures can be obtained. In addition to segment dendrites into fine pieces, melt flow can meanwhile rotate or transit fragments and thus disorder the crystallographic relation of crystals. Fig.5 shows EBSD map of the AZ91D alloy solidified at f=900 Hz, indicating that the grain structure is random and there is no preferential crystallographic orientation. Note that the triangle beside the EBSD map indicates the reference for decoding the inverse pole figure during analysis. This reference triangle will be used for the subsequent mapping.

Fig.5 EBSD map of AZ91D alloy solidified at vibration frequency of f=900 Hz
With the further increase of vibration frequency, the relative displacement covered by the mobile solid decreases. One example is that at f=3 500 Hz, the leading distance is about 12 μm, which is less than the average diameter of the measured grains size. Therefore, this relative leading distance covered by the mobile solid may be too short to agitate severe fluid flow and thus the fragmentation of crystals cannot be fully completed, which results in a coarse structure. This analysis also applies to the higher frequencies, e.g. f=5 000 Hz, at which the leading distance is decreased to about 8 μm.
Besides the Lorentz force during EMV processing, the hexagonal close packed Mg crystal is subjected to a magnetic torque due to the anisotropic magnetic susceptibilities along c-axis and a(b)-axis. For the present Mg-based alloy, there is a positive difference for the magnetic susceptibilities along c-axis and a(b)-axis [16] and thus the basal plane of the crystals should be rotated to align perpendicular to the direction of the magnetic field. Because the sectioning plane is perpendicular to the direction of the magnetic field, the observation plane should be the basal plane. Fig.6 shows an EBSD of the AZ91D alloy solidified at f=3 500 Hz, in which only a unique color can be identified. When referring the reference triangle for decoding the color pixel in Fig.5, one can readily tell that all grains have only a single crystallographic orientation to their (0001) plane. This should be the indirect evidence to demonstrate that melt flow produced at this high frequency, if it really exists, is so weak that it cannot stir the crystals to distribute randomly. Instead, the strength of the magnetic alignment prevails over that of melt flow and thus the static magnetic force aligns crystal to orientate to their easy magnetization plane of (0001). This is true not only at f=3 500 Hz, but also at high frequencies, e.g. f=5 000 Hz, as confirmed by X-ray diffraction in a large area[10].

Fig.6 EBSD map of AZ91D alloy solidified at vibration frequency of f=3 500 Hz
5 Conclusions
1) It is found that for both alloys of AZ31 and AZ91D the microstructures at low and high frequencies are rather coarse with developed equiaxed rosette dendrites. At medium vibration frequencies from f=500 Hz to f=2 000 Hz for AZ31 and f=900 Hz for AZ91D, the refined microstructures with equiaxed grains can be obtained.
2) With respect to the structure formation mechanism, there is a significant difference in electric resistivity between a solid and a liquid in the mushy zone of the alloy, which makes the solid move faster than the liquid, thus generating uncoupled motion between the mobile solid and the sluggish liquid during EMV processing, from which melt flow is initiated. Further analysis reveals that the melt flow intensity is strongly related to the vibration frequency. Meanwhile, the effect of the static magnetic field on structure formation is incorporated, which enables the crystals to align to their easy magnetization direction and thus yields a highly oriented texture at a high vibration frequency, e.g. f=3 500 Hz for the AZ91D alloy.
Acknowledgements
The authors are grateful to Mr. D. KAMIKIHARA for his technical assistance in ingot preparation and Dr. N. SAITO for his help in EBSD analysis.
References
[1] QUESTED T, GREER A. The effect of the size distribution of inoculant particles on as-cast grain size in aluminum alloys [J]. Acta Mater, 2004, 52: 3859-3868.
[2] VIVES Ch. Effects of forced electromagnetic vibrations during the solidification of aluminum alloys: Part 1. Solidification in the presence of crossed alternating electric fields and stationary magnetic fields [J]. Metall Mater Trans B, 1996, 27: 445-455.
[3] RADJAI A, MIWA K, NISHINO T. An investigation of the effects caused by electromagnetic vibrations in a hypereutectic Al-Si alloy melt [J]. Metall Mater Trans A, 1998, 29: 1477-1484.
[4] RADJAI A, MIWA K. Structural refinement of grey iron by electromagnetic vibrations [J]. Metall Mater Trans A, 2002, 33: 3025-3030.
[5] MIZUTANI Y, KAWAI S, MIWA K, YASUE K, TAMURA T, SAKAGUCHI Y. Effect of intensity and frequency of electromagnetic vibrations on refinement of primary silicon in Al-17% Si alloy [J]. Mater Trans, 2004, 45: 1939-1943.
[6] MIZUTANI Y, KAWATA J, MIWA K, YASUE K, TAMURA T, SAKAGUCHI Y. Effect of frequency of electromagnetic vibrations on microstructural refinement of AZ91D magnesium alloy [J]. J Mater Res, 2004, 19: 2997-3003.
[7] DONG J, CUI J, YU F, BAN C, ZHAO Z. Effect of low-frequency electromagnetic casting on the castability, microstructure, and tensile properties of direct-chill cast Al-Zn-Mg-Cu alloy [J]. Metall Mater Trans A, 2004, 35: 2487-2494.
[8] ASAI S. Application of high magnetic fields in inorganic materials processing [J]. Model Simul Mater Sci Eng, 2004, 12: R1-R12.
[9] LI M, TAMURA T, MIWA K. Controlling microstructures of AZ31 magnesium alloys by an electromagnetic vibration technique during solidification: From experimental observation to theoretical understanding [J]. Acta Mater, 2007, 55: 4635-4643.
[10] LI M, TAMURA T, MIWA K. On the role of vibration frequency on the solidification of AZ91D magnesium alloys during electromagnetic vibration [J]. J Mater Res, 2009, 24: 145-155.
[11] VIVES Ch. Grain refinement in aluminum alloys by means of electromagnetic vibrations including cavitation phenomena [J/OL] JOM-e 1998, 50. http://www.tms.org/pubs/journals/JOM/9802/ Vives/Vives-9802.html.
[12] AVEDESIAN M, BAKER H. Magnesium and magnesium alloys [M]//ASM Specialty Handbook. Materials Park, OH: The Materials International Society, 1999: 9-15.
[13] DAVIS J R. Aluminum and aluminum alloys [M]//ASM Specialty handbook. Materials Park, OH: The Materials International Society, 1993: 641.
[14] HELLAWELL A, LIU S, LU S Z. Dendrite fragmentation and the effects of fluid flow in castings [J]. JOM, 1997, 49(3): 18-20.
[15] FLEMINGS M C. Behavior of metal alloys in the semisolid state [J]. Metall Trans A, 1991, 22: 957-981.
[16] WU C, LI S, SASSA K, CHINO Y, HATTORI K, ASAI S. Theoretical analysis on crystal alignment of feeble magnetic materials under high magnetic field [J]. Mater Trans, 2005, 46: 1311-1317.
(Edited by YANG Bing)
Corresponding author: M. J. LI; Fax: +81-52-736-7406; E-mail: li.mingjun@aist.go.jp
DOI: 10.1016/S1003-6326(09)60277-6

