J. Cent. South Univ. Technol. (2008) 15(s1): 033-038

DOI: 10.1007/s11771-008-309-z

Thermal-rheology effect and temperature field of engineering polymers

LI Zhi-da (李之达)^{1, 2}, WANG Hua-ping (王花平)², HUANG Jing(黄 婧)²

(1. Department of Mechanic, Huazhong University of Science and Technology, Wuhan 430093, China)

(2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China)

Abstract: The formation and evolution laws of the defect temperature field, heat dissipation in the process of defect evolution were studied. On the basis, the formation and evolution laws of the defect temperature field were investigated, the interaction among defects in the process of defect evolution was carried out. The numerical simulation of the temperature field of ABS was made. The results show that the process of defect evolution is one of energy dissipation, in which the defect temperature field forms due to that its heat dissipation possesses fractal property and its fractal dimension not only relates to the interaction among the defects, but also is the function of time, this incarnates the efficiency of coordinated actions of striding over the different gradations in the process of defect evolution and among gradations. The increase of the local temperature with the increase of deformation-induced heating effect in ABS is obvious. Moreover, the shape of plastic zone and inner heat source density function has big effect on the temperature field.

1 Introduction

In order to study defect evolution process and explore the failure mechanism of material, our academic group launched fruitful discussions on the defect evolution laws at variant gradations and related characteristics^[1]. The continuum damage mechanics represented by KACHANOV^[2], who used the  internal variable to treat the damage problems. CURRAN et al^[3] considered that the damaged state of materials would depend on the statistic distribution law and evolution characteristics of their internal micro-defects, and put forward the model of nucleation and propagation. After 1970s, the research on critical phenomena raised the exceeding percolation model of damage and failure of material and introduced the scale invariance and the method of renormalization-group into the failure problem of material^[4-5]. In recent years, the research on the growth model of damage and failure of material was quite active, too. All these kinds of the researches on the models of defect evolution have much common, combining mechanics, physics, material science, mathematical statistics and non-linear science tightly to study the problems of defect evolution, and adopting the method in combination with the theoretical analysis, experimental research and numerical analogue by electronic computer^[6-8].

The investigation aimed to study the formation, distribution and the evolution law of the defect temperature field in the evolution process. Some authors^[9] considered that the average interaction among these micro-cracks could change the macro field. So, the nucleation, growth of defects and the interaction among these defects could be investigated indirectly through the variation of the macro field. The characteristics in the process of defect evolution would be the rheology and energy dissipation in the process. Heat dissipation was regarded as the essential part of energy dissipation, its main manifestation should change the temperature. Therefore, we can adopt the variation of the macro field defect temperature field to investigate the defect evolution process.

2 Basic principle

In view of the rheology of bodies with defects, the external factors, such as temperature, time, stress and environment, may cause the production of flow and deformation in material, even failure and accompany by energy dissipation^[10-12]. The increment ?E of the energy in unit volume of material within unit time is expressed as

                             (1)

where  ?E₁ is the effective energy; ?E₂ is the dissipated energy.

?E₂≥0, ≥0                            (2)

Generally, the dissipative energy may be resolved as

                             (3)

here  ?H is the heat dissipation; ?Q is the energy dissipation of the other forms except heat. Both satisfy Eqn.(2). Introducing the heat dissipation factor, the heat dissipation for energy dissipation is

                                 (4)

Defining the heat dissipation coefficient , let

                                (5)

here  θ is temperature. Further, deformation may be resolved into elastic deformation ?ε_e and non-elastic deformation ?ε_d. So, there would be

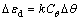                               (6)

This is the theoretical basis for the formation of the defect temperature field in the process of defect evolution.

From the principle of energy conservation, the variation rate of the inner energy  in unit volume of material would be

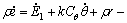??q                     (7)

where   r is the function of internal heat supply rate; q is the vector of heat flow. Compared with the  partial energy equilibrium equation related to continuum, the defect local temperature field may produce an appended heat-source within material, even without the internal heat supply (r=0), the defect local temperature field should also exist, this was confirmed in our tests.

The stress strain curve of the material is shown in Fig.1, which determines that the dissipation energy E₂ in the defect evolution process would be the triangular area of OPR. Obviously, the area is related to the slope of the straight lines PR and OR, that is, the energy dissipation of the material will be related to the factors, such as the increment of non-elastic deformation, the loss of the mechanics characteristic in the process of defect evolution.

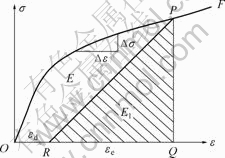
Fig.1 Stress—strain curve of material

The measurement of temperature field can determine the heat dissipation ?H in defect evolution process by the defect evolution law.

3 Experimental

3.1 Sample and measurement system

Taking ABS(Acrylonitrile-Butadient-Styrene)sheet as the sample, the defects with different distribution forms, the sample shape, dimension and defect distribution are shown in Fig.2. In Fig.2 the defect size , defect number N, the distance between defects d_i and the angle θ_i between d_i and loading direction are all adjustable parameters.

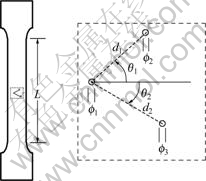
Fig.2 Sample shape and defect distribution

The loading equipment is the fatigue test system of LST-50S mode electro-liquid serve material. And tape-recorder and double-passageway analyzer simultaneously acquire the curves of load—time, displacement—time, still the stress—strain curve is obtained. The achieved results according essentially with the stress-strain curve are shown in Fig.1.

The temperature measure system is 6T61 mode infrared imaging-meter with high-sensitivity and non-touched type and the synchronized-signal trigger and numerical analog tape-recorder are adopted so as to achieve the temperature variation at any time, which is synchronous with loading information and at any point on the surface of the sample.

Afterwards, the reader and the scanner put the obtained experimental results in microcomputer. At last, the test data and images are analyzed.

3.2 Results and analyses

3.2.1 Formation of defect temperature field and its variation with time

Under the condition of single-axle tension with controlled displacement speed, the temperature near defect would vary with time.

Regardless of the distribution of defects (including macro cracks), at the beginning of loading, the body with defects shows a process of temperature drop. The variation laws of temperature at all the points near the defect location are nearly identical, they all first drop slowly 0.5-1.0 ℃.

After a period of time, as the load gets greater, the stress—strain relation of corresponding material becomes non-linear. The defect temperature field begins to form, then the damage will appear in the sample.

When the load increases, the isotherm would produce butted penetration. At last, the temperature will rise rapidly till the maximum before the sample fails. In Fig.3, there are a few thermal imaging pictures for the formation of defect temperature field and its process of variation with time.

From Fig.3, we can obtain the isotherm of any value of temperature on the surface of sample at any time in the process of defect evolution, and get the isotherm of the temperature field near defect which evolves with time, while the butted penetration of the isotherms would affect the direction and degree of defect evolution. Fig.4 shows the evolution process with time.

As the thickness of sample is much less than the sizes in other directions, the time of heat transfering along the thickness direction would be rather less than that along other directions. Because heat propagation is much faster than the response produced by the effectiveness of rheological mechanics, the heat dissipation is the main part of energy dissipation. So, the isotherm evolution with time (shown in Fig.4) shows essentially the variation of energy dissipation in the process of defect evolution.

3.2.2 Interaction between defects

The experimental results of the initial defect samples with different relative positions are obtained.

The relative positions(d_i , θ_i) between defects have great effect on the displacement of the body with defects, loads and the temperature field in defect localized area. The less the distance d_i between defects is, the stronger the effect will be. When the distance d_i between the defects becomes greater, the effect will weaken, even disappear.

The angle  between the connected line in defects and the load direction also has great effect on the displacement of the body with defects, load and the temperature field in defect localized area. When , the effect is strongest with  lessening, the effect is weakened; when , there nearly is no effect. The interaction between defects and temperature fields is shown in Fig.5. Fig.5(a) shows the state of an isolated defect, Fig.5(b) shows the stated of double defects, and Fig.5(c) shows the state of three different distribution defects.

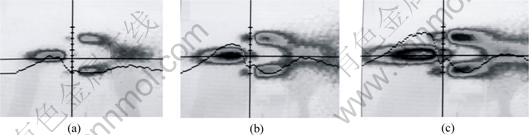
Fig.3 Formation of defect temperature field and its variation with time: (a) t=43 s; (b) t=45 s; (c) t=47 s

Fig.4 Isotherm evolution with time at defect temperature field of 15.40 ℃: (a) t=48 s; (b) t=50 s; (c) t=52 s; (d) t=54 s; (e) t=56 s

Fig.5 Interaction between defects and temperature field: (a) Isolated defect; (b) Double defects; (c) Three different distribution defects

4 Results and analysis

4.1 Statistical similarity

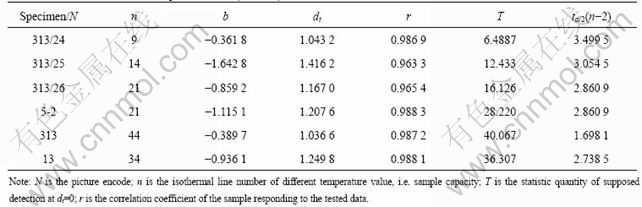
Let the measured perimeter L_i of the isotherm of the defect temperature field in the test and its enclosed area A_i be analyzed correlatively under a bi-logarithm coordinate system. According to the tested data, the statistic quantity T can be structured and calculated.  Table 1 shows the statistic data of the defect temperature field.

From the statistic data, we can find that the correlation coefficient r＞0.96, which shows that the perimeter L_i of isotherm of the defect temperature field and its enclosed area A_i under the bi-logarithm coordinate system possess very good linear correlation. Therefore, the regression equation may be obtained.

                      (8)

Under the condition of nakedness level , the regression of Eqn.(8) is obvious, d_t is the fractal dimensionality of the curve L_i.

4.2 Heat dissipation

Because the thickness of the sample h << 1, and the temperature variation along the thickness direction is small, it is considered that the  isothermal surface should be vertical to the surface of the sample. Suppose the mass density ρ of the material in the process of defect evolution and the specific heating capacity c are constants by Eqns.(3)-(5), the total heat dissipation of the body would be where  ?A_i is the area enclosed by isotherms i and i-1.

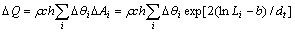
By calculation, we can see that the fractal dimensionality d_t of isotherm L_i is a function of time, which manifests the different gradations and cooperative actions of micro and macro-scopes factors in the process of defect evolution, and the fractal dimensionality d_t of isotherm L_i would be related to the defect distribution, i.e., the defect evolution would be related to the interaction between defects.

5 Numerical simulation

5.1 Shape of plastic zone

Heat dissipation is regarded as the essential part of energy dissipation. Therefore, we can adopt the variation of the temperature field to investigate the plastic deformation. The boundary of plastic zoon is similar to the isotherm of temperature.

Taking ABS specimen with a defect for an example by the experiment of temperature field, the boundary of plastic zoon can be express as

  (9)

5.2 Control equation of temperature field

Based on the laws of irreversible thermodynamics, considering the thermo-mechanical coupling in the material deformation and fracture processes, the control equation of the temperature field becomes^[13]

             (10)

where  and G are Lamé Constance. The internal heat source density function can be taken as

 (n＞1)          (11)

On the boundary of plastic zoon, satisfying:

 (r­_S≥r_m)                        (12)

And in the plastic zoon, satisfying:

Table 1 Statistic list of defect temperature field (α＝0.01)

          (13)

Taking k=0.2 W/mK, ρ=1 040 kg/m³, c=1 400 J/(kg?K), Q can be determined by the experiment of temperature field.

Using Mathcad, the temperature field of ABS specimen under uniaxial tension condition can be obtained. The isotherm evolution with time is shown in Fig.6. The isotherm evolution with n is shown in Fig.7. The isotherm evolution with m is shown in Fig.8.

Fig.6 Isotherm evolution with time (n=2, m=1)

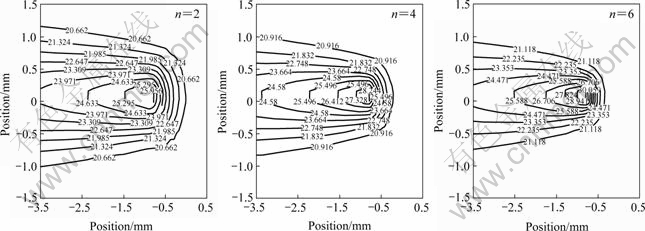
Fig.7 Isotherm evolution with n (t=52 s, m=1)

Fig.8 Isotherm evolution with m (t=46 s, n=2)

6 Conclusions

1) The temperature fields produce in the process of macro or micro crack propagation, the meso-defect evolution possesses self-similarity.

2) The defect evolution process exhibits the interaction between defects, mutual restraint and influence and follows by the process of heat dissipation. The defect evolution process can be inspected indirectly by the variation of the macro temperature field.

3) The isotherm surface of defect temperature field possesses the fractal characteristic, and the fractal dimensionality can be taken as the measurements to study the defect evolution, the interaction between defects and energy dissipation.

4) The numerical simulation of the temperature field of ABS is made. The local temperature rise by deformation-induced heating effect in ABS is obvious. Moreover, the shape of plastic zone and inner heat source density function has big effect on the temperature field.

References

[1] XIA Meng-fen, HAN Wen-sheng, KE Fu-jiu, BAI Yi-long. Statiscal meso-scopic damage mechanics and damage evolution induced catastrophe(Ⅰ)[J]. Advances in Mechanics, 1995, 25(1): 1-40. (in Chinese)

[2] KACHANOV L M. Introduction to continuum damage mechanics[M]. Netherlands: Dordrechet Maritinus Nijhoff Publishers, 1986.

[3] CURRAN D R, SHOCKEY D A, SEAMAN L. Dynamic fracture criteria for a polycarbonate[J]. J Appl Phys, 1973, 44(9): 4025-4038.

[4] SMALLEY R F, TURCOTTE D L, SOLLA S. Renormalization group approach to the stick-slip behavior of faults[J]. J Geophys Rev, 1985, 90(B2): 1894-1900.

[5] TURCOTTE P L, SMALLEY R F. Statistical models for the fracture of disordered media[M]. Elsevier Science Press B.V., 1990.

[6] LUO Wen-bo, YING Ting-qing, LI Zhi-da. Experimental studies on the temperature fluctuations in deformed thermoplastics with defects[J]. J Solid & Structures, 2000, 37(6): 887-897.

[7] LI Zhi-da, LIU Hong-jun, ZHANG Rong-feng. Research on time-temperature stress superposition principles of PMMA’ crazing damages under creep condition, advances in rheology and its applications[C]// Proceedings of the 4th Pacific Rim Conference on Rheology. Changsha: Central South University Press, 2005: 739-744.

[8] LI Zhi-da, YI Hui, ZHANG Rong-feng. Experimental research on temperature dependence of PMMA’s crazing damage[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering, 2005, 29(4): 478-480, 490.

[9] XIA Meng-fen, KE Fu-jiu, LU Yong-hua, BAI Yi-long. Effects of stochastic extrension in ideal microcrack system[J]. Science in China (Series A), 1991, 34(5): 579-589.

[10] YUAN Long-wei. Rheology of bodies with defects[M]. Beijing: National Defence Industry Press, 1994.

[11] YUAN Long-wei, LI Zhi-da. On the rheological and dissipative phenomena in the process of crack propagation(Ⅰ), (Ⅱ)[J]. Nat Sci J Xiangtan Uni, 1989, 11(1): 33-63.

[12] YUAN Long-wei, ZHI Rong-bing, LI Zhi-da. Rheology fracture[M]. Beijing: National Defence Industry Press, 1992.

[13] CHRISTENSEN R M. Theory of viscoelasticity, an introduction[M]. New York: Academic Press, 1982.

(Edited by LI Yan-hong)

Foundation item: Project(10372074) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: LI Zhi-da, Professor; Tel: +86-27-62388188; E-mail: zhidali@163.com