DOI: 10.11817/j.issn.1672-7207.2019.02.012
运动单站单基线解模糊定位算法
郭立民，谢强，陈涛，王梦馨
(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001)
摘要：针对传统干涉仪多频段测向定位系统复杂、单基线测向模糊等问题，提出一种基于运动单站单基线对地面静止辐射源解模糊无源定位方法。首先，建立基于模糊相位差几何特性的无源定位模型，然后推导出在最大似然比条件下模糊相位差的代价函数，通过樽海鞘群优化算法估计辐射源位置，最后推导出该无源定位模型下的定位误差几何精度因子(GDOP)。研究结果表明：本文所提出的方法能够在低信噪比条件下达到较高的定位精度，仅利用单基线干涉仪即可对多个频段辐射源进行定位。
关键词：无源定位；单站；干涉仪；相位差；樽海鞘群算法
中图分类号：TN971 文献标志码：A 文章编号：1672-7207(2019)02-0336-07
A single moving observer ambiguity resolution locating algorithm using single baseline interferometer
GUO Limin, XIE Qiang, CHEN Tao, WANG Mengxin
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract: To deal with the complexity structures of multiple frequency bands in the use of multichannel phase interferometers and the ambiguity of direction finding in using single baseline interferometer, a single moving observer ambiguity resolution passive location algorithm was proposed for the static ground emitter. Firstly, the passive location model of ambiguous phase difference(PD) based on geometric characteristics was established. Then the cost function of PD in the maximum likelihood principle was derived. The emitter position was then estimated by the salp swarm algorithm(SSA). Finally, the geometrical dilution precision (GDOP) of PD in the single observer passive location model was derived. The results show that the proposed method can achieve high positioning accuracy under low signal-to-noise ratio (SNR) conditions, and multiple frequency band emitters can be located only by using single baseline interferometer.
Key words: passive location; single observer; interferometer; phase difference; salp swarm algorithm
运动单站无源定位技术利用单个观测站被动接收非合作辐射源雷达或通信信号进而确定其位置，其在电子侦察、远距离预警及监视等领域受到了广泛的关注和研究[1-4]。为了提高测角精度，测向交叉定位需要采用长基线干涉仪比相测角的方法，但在基线长度大于信号的半波长时，相位差测量会出现模糊现象[2-3]，测向系统就必须采用多天线接收通道解相位差模糊，将导致系统复杂度高、天线间通道幅相不一致、载荷加重等问题[4]。同时，由于多天线间的指向关系，可能存在仅有2个天线能够接收到辐射源信号的情况，因此，有必要研究单基线定位方法。采用一维长基线干涉仪定位时，在无法测量得到无模糊相位差的条件下，不能采用解相位模糊测向交叉定位方法，而直接利用所测得相位差估计目标位置是解决该问题的方法之一。针对此类问题，TIRER等[5-6]基于辐射源信号的多普勒频移信息，直接利用接收信号进行定位方法建模，并提出了一种高分辨率的定位方法；TIRER等[7]分析了该直接定位方法的性能，验证了该方法的有效性；OUYANG等[8]利用跳频信号在频域中的稀疏性，在频域中构造互相关函数矩阵，通过在二维网格中搜索该矩阵的最大特征值，得到跳频信号的位置估计；陈曦等[9]基于干涉仪模糊相位差直接进行辐射源位置估计，省去了角度测量的过程；OISPUU等[10]直接利用空间谱分解的方法建立定位模型，省去了经典的空间谱测向过程；张敏等[11]提出一种基于信号子空间分解的单个长基线干涉仪直接定位方法，该方法采用量子粒子群优化方法获得定位初始值，再利用牛顿迭代方法得到精确估计值，定位精度较高。同时，张敏等[12]还提出了基于长短基线干涉仪相位差测量的多角度距离参数化高斯和滤波定位解算方法，在无相位差模糊、低信噪比下，该方法定位性能优于测向定位方法性能，且可以覆盖多个频段辐射源；王鼎等[13]同样基于单个运动阵列，针对相位调制信号的恒包络特征，提出一种新的定位模型，进一步提高了定位精度；王鼎等[14]分析了在信号波形已知条件下的多目标直接定位算法的理论性能，针对不同目标信号波形相关性会影响算法性能的缺点，提出了改进的多目标直接定位算法。利用干涉仪模糊相位差的几何特性，本文提出一种基于运动单站单基线解模糊定位算法；该方法仅以双通道单基线测得的模糊相位差为观测量，在观测器作曲线飞行的一段观测时间内，利用观测平台的机动带来的不同时刻相位差测量值之间的差异性，建立辐射源位置的代价函数，采用樽海鞘优化算法(SSA)行辐射源位置估计；最后，推导出该单基线模型的定位误差几何精度因子(GDOP)。
1 定位模型及原理
定位场景示意图如图1所示（其中t1~tN为不同的观测时间）。假设在某一观测时间内，运动观测器接收到某个地面静止辐射源发射的信号，平台基线垂直于机身安装，观测器沿曲线轨迹运动。利用观测器上的单基线干涉仪可多次测量来波方向相位差，再结合自身位置和姿态信息即可实现对辐射源位置的估计。而传统测向定位方法通过测量接收信号的相位差信息，然后解相位差模糊得到角度估计，通过交叉定位方法解得辐射源位置。该方法在远距离低信噪比情况下定位性能急剧下降，且由于角度估计误差增大导致存在测向定位虚假点的问题[15]。
图1 定位场景示意图
Fig. 1 Schematic diagram of locating scenario
假设辐射源位置为
，信号频率为f0。运动观测平台在第n个观测时刻tn的位置为
，干涉仪基线指向矢量为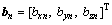
，则无模糊相位差
为
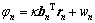(1)
式中：
(其中λ为波长) ；rn为辐射源到观测器的单位方向矢量，
(其中rn为辐射源xs与xn之间距离)，
）；wn为相位差测量随机误差，且假设其服从均值为0，方差为
的高斯分布；n=1，2，…，N。另外，假设不同测量时刻误差之间相互独立，且方差均为
。
由于干涉仪系统量测相位差只能在±180°范围内，由式(1)可知当基线长度大于λ/2时，实际测量的相位差φn可能存在2π的模糊：
(2)
从几何角度分析，单基线干涉仪1次观测收到来波信号相位差，若基线长度小于λ/2，对应着唯一的来波方向，可直接进行交叉定位；若基线长度大于λ/2，则对应着来波的多个方向，这些方向对应着1簇定位线。假设经过一段时间，基线在另一个位置又获得1簇定位线，2簇定位线相交得到的1组交点就对应辐射源位置的1组模糊解。在观测器运动的条件下，不同时刻的位置上干涉仪基线姿态存在差异性，正是这种差异性使得在多次测量的相位差对应的定位线中，只有经过辐射源的定位线才能交于1点[11]。
2 定位方法
本文考虑在双通道长基线干涉仪测量设备下，充分利用目标辐射源与观测平台之间的相对运动信息，以相位差为观测量，选取合适的代价函数，将定位模型的复杂非线性寻优问题转化为求解目标位置的多峰函数极值问题，并采用樽海鞘群优化算法获取目标位置的参数估计。
2.1 代价函数的选取
假设在某一段时间内共进行了N次测量，每次测量的相位差误差服从高斯分布，仅利用相位差测量值估计目标辐射源位置x的最大后验估计可表示为
。无源定位场景中，目标可能来自任何方向，当目标没有先验信息时，将最大后验估计变为最大似然估计
。
假设
每次测量相互独立，且误差符合高斯分布
，则条件概率可写为
(3)
条件概率的具体表达式可写为
(4)
式中：
为第n次相位差观测量的平均值；
为相位测量方差。假设每次相位差观测量误差服从相互独立的高斯分布，故各个测量时刻的相位差均值即为观测器相对于真实辐射源位置的理论值。该值由测量时观测平台的位置、观测器姿态状态和辐射源位置等因素共同决定。
由自然对数函数的单调性，对式(4)取自然对数函数变换，可得到最终状态估计公式为
(5)
2.2 樽海鞘群定位算法
MIRJALILI等[16]以樽海鞘的群体行为特征为启发，建立了樽海鞘链的数学模型，提出了樽海鞘群优化算法(SSA)。SSA不同于灰狼优化 [17](grey wolf optimization, GWO)和粒子群优化算法[18](particle swarm optimization, PSO)，后两者进行群体位置更新时全部个体都跟随最优者进行移动，若最优者前期搜索不充分，则后期常常会导致整个群体陷入局部极值而导致计算错误。而SSA是采用首尾相接组成链的形式，顺次跟随着移动。在樽海鞘链中，领导者对环境有着最优的判断，排在链的首端，但其不直接影响整个群体的移动方向，仅影响距自己最近的樽海鞘位置更新。同理，第2个樽海鞘再直接影响第3个樽海鞘，以此类推形成了完整的樽海鞘链。可见，SSA很好地平衡了寻找全局最优解过程中的探索行为和开发行为，使求解全局最优值更具有可靠性，且较其他优化算法控制参数极少。
NFL(no-free-lunch)理论[19]认为不同智能算法在解决不同优化问题具有不同的性能。因此，本文采用SSA解决模糊相位差无源定位问题，其基本流程如下。
1) 确定定位场景观测有效区域。根据观测器信号的探测能力、飞行高度等因素选定定位有效观测区域，提供算法初始化基本参数。
2) 种群初始化。设搜索状态空间是K×Q维的欧式空间，其中K为樽海鞘群的规模，Q为空间维数。假设空间中存在食物
，樽海鞘的位置为
(k=1，2，…，K)。搜索空间的上界表示为
，下界为
。在三维定位空间当中，随机初始化种群表达式可写为
(6)
式中：
表示向量
和向量
的Hadamard积。
3) 选定目标食物。由于实际定位时无法获得任何辐射源(即食物)的先验信息，故将樽海鞘群中最优适应度的位置作为当前迭代的食物位置。
4) 领导者与追随者位置更新。首先，选定领导者与追随者，排除作为目标食物的樽海鞘，将群体中剩余的樽海鞘一分为二，其中，前一半视为领导者，后一半视为跟随者。然后，进行领导者和追随者位置更新，领导者更新方式为
(7)
式中：Xqk表示对第k个樽海鞘第q维坐标值进行更新；q=1，2，…，Q；c1，c2和c3均为控制参数，其中c2与c3均是[0，1]之间的随机数，其作用为增强领导者移动的随机性与多样性；c1为主要的控制参数，控制整个群体搜索过程中的全局搜索性能，其表达式为
(8)
式中： lmax为最大迭代次数。
追随者更新方式为
(9)
式中：Xk为更新前第k个追随者位置；
为更新后追随者的相应位置。
5) 计算适应度。利用选定的代价函数计算更新后的群体中所有的樽海鞘个体适应度，同时选择其中最优个体，并将该个体适应度与当前目标食物适应度进行比较，选择其中更优者作为下一次迭代的新的目标食物位置。
6) 判断当前定位是否结束。若当前迭代满足结束条件，则停止计算，将当前选定的食物作为定位结果输出；若不满足，则返回步骤4)继续迭代。
樽海鞘群算法(SSA)流程如图2所示。
图2 樽海鞘群算法流程图
Fig. 2 Flow chart of SSA
3 定位误差GDOP
由于2π的取模运算，直接计算模糊相位差定位方法的GDOP较困难，因此，以无模糊相位差GDOP作为本文方法定位性能的评价指标。由式(1)可知影响辐射源目标定位精度因素主要包括相位差测量误差、载频测量误差、观测平台位置及基线姿态误差。下面参考文献[20]中的推导方法，对定位误差进行分析。
对式(1)求全微分得：
(10)
式中：
；
；
；
；
为第n次测量观测平台坐标位置；
为第n次测量干涉仪中天线坐标位置；
为第n次测量的信号载频。
在一段观测时间内，观测平台对辐射源进行多次观测后，可将所有的观测数据写成矩阵形式：
(11)
式中：
，为不同时刻测量相位差；
，为影响定位精度的不同因素，j=1，2，3。Aj表达式如下：
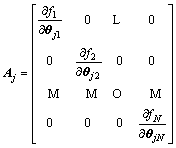(12)
式中：
，为信号载频；
，为平台位置；
，为干涉仪基线矢量；n=1，2，…，N。
H为测量函数对辐射源坐标位置的求导矩阵，其表达式如下：
(13)
假设RZ为相位差协方差阵，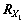
为载频测量协方差阵，
为平台位置协方差阵，
为基线矢量协方差阵，则定位误差的协方差矩阵PX为
(14)
式中：
。
根据式(14)可以得到理论误差GDOP为
(15)
4 仿真实验及分析
本文采用基于模糊相位差的SSA算法进行仿真实验，仿真场景及相关参数设置如下：观测平台飞行高度为3 km，沿X轴方向作曲线机动飞行，速度为300 m/s，平台初始时刻位置为(0，0，3) km，采用双通道一维干涉仪基线设置方式，基线长度为3 m，干涉仪垂直于机身安装。观测平台自身位置和姿态信息通过导航设备获得，假设位置测量精度为5 m，基线姿态测量精度为0.5 mm。辐射源位置为(105，100，0) km，辐射源信号频率为2 GHz，测频精度为1 MHz，观测器每次定位观测时间间隔为0.5 s。观测平台采用S形机动方式，即观测器沿X轴方向飞行，径向机动距离2 km。
1) 仿真1：定位精度GDOP分析。
根据前面所推导出的定位GDOP，假设辐射源信号载频为2 GHz，观测时间为60 s，根据式(15)得到在不同测量精度条件下辐射源定位精度分布结果，如图3所示(其中tg为每次观测时间间隔，
为相位差误差，
为基线姿态测量误差，其余参数与上述仿真场景参数一致)。
由图3可知：单站单基线相位差无源定位的误差关于运动平台轨迹呈对称分布。对比图3(a)和(b)可知：当信号载频为2 GHz时，天线姿态测量误差对定位精度影响较小，在一般情况下可以忽略。由图3(b)和(c)可以看出：相位差测量误差对定位精度影响较大，要实现高精度无源定位，相位差测量精度最好能够达到10°。由图3(c)和(d)可以看出：在相同运动轨迹和观测时长情况下，增加观测次数可以在一定程度上提高定位精度，同理也可以通过增加观测时长来提高定位精度。
2) 仿真2：测向模糊SSA定位。
在基本的仿真场景基础上和不同相位差测量随机误差下，验证本文定位算法的定位性能。本算法仿真中设置最大探测距离Rmax=200 km，樽海鞘数为30，迭代次数为500，领导者和跟随者数目各占一半。仿真中取相位差测量误差在5°~60°范围内，采用本文提出的定位方法对固定辐射源进行位置估计，设置Monte Carlo实验次数为200次。在相同的仿真条件下，本文方法与其他方法的定位均方根误差比较结果见图4。其中，SSA-PD为本文方法；GWO-PD为文献[17]中算法；PSO-PD为文献[9]中算法；CRLB为克拉美-罗下界。
由图4可知：在测向模糊条件下，本文方法能够在较低信噪比情况下实现对辐射源目标的定位估计，其定位精度高于文献[9]中定位方法的精度，且能够接近CRLB。在相位差误差为10°时，本文方法定位精度达到1.8%，且在整个误差范围内，定位精度也高于GWO算法的精度，可见该算法后期收敛效果较GWO算法更具有优势。
图3 不同条件下辐射源定位精度仿真结果
Fig.3 Simulation results of locating accuracy of emitter under different conditions
图4 测向模糊条件下不同算法的定位性能
Fig. 4 Locating performance of different algorithms in condition of ambiguous direction finding
3) 仿真3：不同频段辐射源。
为进一步分析本文方法对不同频段辐射源的定位性能，采用与仿真2中相同的定位场景。在仿真过程中，为统计定位性能，采用200次Monte Carlo重复试验，将单次定位误差大于5倍CRLB判断为错误定位结果。正确的定位概率即解模糊概率Pc表达式为
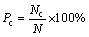(16)
式中：Nc为N次重复试验中正确定位的次数。
当相位差测量随机误差为10°，定位观测累积时间为60 s时，不同频率辐射源(2~18 GHz)下3种算法的定位正确概率的仿真结果见表1。
从表1可以看出：本文方法即SSA-PD可以对该频率范围辐射源目标进行有效定位，可见本文算法适用于干涉仪天线布阵要求较高及系统载荷空间小的定位场景当中；随着频率增大，正确解相位差模糊概率有所下降，将影响算法定位性能。由此可知：本文算法在2~10 GHz频段内辐射源定位性能较好，在10~18 GHz频段内辐射源定位性能有限；其次，GWO和SSA正确解模糊定位性能相当，仿真中使用的整体成员个数为30，较文献[9]中方法的解模糊性能有较大提升，可见本文所采用算法在前期的全局搜索性能较好。
表1 不同算法对不同频率辐射源的定位正确的概率
Table 1 Probabilities of locating correctly of different algorithms for emitters with different frequencies %
5 结论
1) 与相位差多峰代价函数的寻优搜索定位相比，本文算法具有明显优势；通过设置适当的参数，本文算法适用于运动单站单基线模糊相位差对地面固定辐射源的定位，且具有良好的定位性能。
2) 在辐射源频率超过干涉仪解模糊频段条件下，本文方法无需采用多基线或阵列天线完成干涉仪测向解模糊过程，仅利用单基线即可完成对宽频段地面固定辐射源定位，可降低系统的复杂性和成本，对有特殊要求的装备(如系统载荷有限等)具有一定参考意义。
参考文献：
[1] 孙仲康, 郭福成, 冯道旺. 等. 单站无源定位技术[M]. 北京: 国防工业出版社, 2008: 1-29.
SUN Zhongkang, GUO Fucheng, FENG Daowang, et al. Passive location and tracking technology by single observer[M]. Beijing: National Defense Industry Press, 2008:1-29.
[2] SHIEH C S, LIN C T. Direction of arrival estimation based on phase difference using neural fuzzy network[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(7): 1115-1124.
[3] XI Wei, YU Bianzhang, WANG Songshan. Theoretical analysis of direct-finding targets with rolling-airframe passive radar by phase interference technique[C]//Proceedings of International Conference on Radar (CIE' 06). New York, USA: Institute of Electrical and Electronics Engineers, 2006: 1-4.
[4] 郭福成, 贾兴江, 皇甫堪. 仅利用相位差变化率的机载单站无源定位方法及误差分析[J]. 航空学报, 2009, 30(6): 1090-1095.
GUO Fucheng, JIA Xingjiang, HUANG Fukan. A single observer passive localization method using phase difference changing rate only and its error analysis[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1090-1095
[5] TIRER T, WEISS A J. High resolution direct position of radio frequency sources[J]. IEEE Signal Processing Letters, 2015, 23(2): 192-196.
[6] TIRER T, WEISS A J. High resolution localization of narrowband radio emitters based on doppler frequency shifts[J]. Signal Processing, 2017, 141: 288-298.
[7] TIRER T, WEISS A J. Performance analysis of a high-resolution direct position determination method[J]. IEEE Transactions on Signal Process, 2017, 65(3): 544-554.
[8] OUYANG Xinxin, WAN Qun, CAO Jingmin,, et al. Direct TDOA geolocation of multiple frequency-hopping emitters in flat fading channels[J]. IET Signal Processing, 2017, 11(1): 80-85.
[9] 陈曦, 朱伟强. 基于新体制的单基线定位技术研究[J]. 航天电子对抗, 2012, 28(4): 53-55.
CHEN Xi, ZHU Weiqiang. The research of locating performance based on signal baseline[J]. Aerospace Electronic Warfare, 2012, 28(4): 53-55.
[10] OISPUU M, NICKEL U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal Processing, 2010, 90(12): 3056-3064.
[11] 张敏, 郭福成, 周一宇. 基于单个长基线干涉仪的运动单张直接定位[J]. 航空学报, 2013, 34(2): 378-386.
ZHANG Min, GUO Fucheng, ZHOU Yiyu. A single moving observer direct position determination method using a long baseline interferometer[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 378-386.
[12] 张敏, 郭福成, 周一宇, 等. 运动单站干涉仪相位差直接定位[J]. 航空学报, 2013, 34(9): 2185-2193.
ZHANG Min, GUO Fucheng, ZHOU Yiyu, et al. A signal moving observer direct position determination method using interferometer phase difference[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2185-2193.
[13] 王鼎, 张刚, 沈彩耀, 等. 一种针对恒模信号的运动单站直接定位算法[J]. 航空学报,2016,37(5):1622-1633.
WANG Ding, ZHANG Gang, SHEN Caiyao. A direct determination algorithm for constant modulus signals with signal moving observer[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1622-1633.
[14] 王鼎, 吴志东, 尹洁昕. 信号波形已知条件下多目标直接定位性能分析及其改进算法[J]. 电子学报, 2017, 45(12): 2881-2889.
WANG Ding, WU Zhidong, YIN Jiexin. A performance analysis and improvement algorithm for multiple-source direct localization with known signal waveforms[J]. Acta Electronica Sinica, 2017, 45(12): 2881-2889.
[15] 张旻, 罗争. 一种基于RSS估计的虚假点消除方法[J]. 电子学报, 2012, 40(10): 2117-2121.
ZHANG Min, LUO Zheng. A new method for eliminating ghost based on RSS estimation[J]. Acta Electronica Sinica, 2012, 40(10): 2117-2121.
[16] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191.
[17] MIRJALILI S, MIRJALILI S M, Lewis A. Grey wolf optimization[J]. Advances in Engineering Software, 2014, 69: 46-61.
[18] GAO Lipeng, SUN Heng, LIU Mengnan, et al. TDOA collaborative localization algorithm based on PSO and Newton iteration in WGS-84 coordinate system[C]//International Conference on Signal Processing. Chengdu, 2016: 1571-1575.
[19] WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82.
[20] 曹东波, 张敏, 姜文利. 单星多普勒变化率无源定位精度分析[J]. 航天电子对抗, 2010, 26(4): 1-4.
CAO Dongbo, ZHANG Min, JIANG Wenli. Accuracy analysis for passive localization of a single satellite based on Doppler rate-of-change[J]. Aerospace Electronic Warfare, 2010, 26(4): 1-4.
(编辑 伍锦花)
收稿日期：2018-04-07；修回日期：2018-06-09
基金项目(Foundation item)：国家自然科学基金资助项目(61571146)；中央高校基本科研业务费专项资金资助项目(HEUCFP201769) (Project(61571146) supported by the National Natural Science Foundation of China; Project(HEUCFP201769) by the Fundamental Research Funds for the Central Universities)
通信作者：郭立民，博士，副教授，从事宽带信号检测、处理和识别研究；E-mail：guolimin@hrbeu.edu.cn
