AZ31B镁合金板材中晶界滑移的晶体塑性仿真
来源期刊:中国有色金属学报(英文版)2021年第1期
论文作者:李子涵 周国伟 李大永 汪华苗 唐伟琴 彭颖红 Hatem S. ZUROB 吴沛东
文章页码:138 - 155
关键词:镁合金;晶界滑移;动态再结晶;多晶体塑性;织构
Key words:magnesium alloys; grain boundary sliding; dynamic recrystallization; polycrystal plasticity; texture
摘 要:建立一种耦合滑移、动态再结晶以及晶界滑移的晶体塑性模型以仿真镁合金的高温变形行为及织构演化。首先,通过实验测量单轴拉伸、压缩后的织构以及显微组织演化,研究AZ31B镁合金在300 °C 的变形机制。结果发现,动态再结晶在应变小于0.2时起到细化晶粒的作用,之后晶界滑移在变形过程中起显著作用。此外,建立晶界滑移模型来评估由晶界滑移产生的应变以及晶粒转动,并与多晶体塑性模型VPSC相耦合。所建立的VPSC-DRX-GBS模型可以很好地计算应力-应变曲线、晶粒尺寸、织构演化以及实验中所发现的拉伸与压缩织构演化显著差异。计算的晶界滑移贡献率在拉伸条件下显著高于压缩条件的,这是由于在拉伸时晶界上更易产生孔洞形核。
Abstract: The aim of present work is to develop a crystal plasticity modeling approach to integrate slip, dynamic recrystallization (DRX) and grain boundary sliding (GBS) for simulating the deformation behavior and texture evolution of magnesium alloys at high temperatures. Firstly, the deformation mechanisms of an AZ31B Mg alloy sheet at 300 °C were investigated by examining texture and microstructure evolution during uniaxial tension and compression tests. DRX refines microstructure at strains less than 0.2, and subsequently GBS plays a significant role during deformation process. A GBS model is developed to evaluate strain and grain rotation induced by GBS, and implemented into the polycrystal plasticity framework VPSC. The VPSC-DRX-GBS model can well reproduce the stress-strain curves, grain size, texture evolution and significant texture differences in tension and compression tests due to GBS. The calculated GBS contribution ratio in tension is obviously higher than that in compression due to easier cavity nucleation at grain boundaries under tension loading.
Trans. Nonferrous Met. Soc. China 31(2021) 138-155
Zi-han LI1, Guo-wei ZHOU2, Da-yong LI1,3, Hua-miao WANG1,Wei-qin TANG1, Ying-hong PENG1, Hatem S. ZUROB4, Pei-dong WU5
1. State Key Laboratory of Mechanical Systems and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China;
2. Department of Materials Science and Engineering, Ohio State University, Columbus, Ohio 43212, USA;
3. Materials Genome Initiative Center, Shanghai Jiao Tong University, Shanghai 200240, China;
4. Department of Materials Science and Engineering, McMaster University, Hamilton, Ontario L8S 4G7, Canada;
5. Department of Mechanical Engineering, McMaster University, Hamilton, Ontario L8S 4G7, Canada
Received 28 March 2020; accepted 12 November 2020
Abstract: The aim of present work is to develop a crystal plasticity modeling approach to integrate slip, dynamic recrystallization (DRX) and grain boundary sliding (GBS) for simulating the deformation behavior and texture evolution of magnesium alloys at high temperatures. Firstly, the deformation mechanisms of an AZ31B Mg alloy sheet at 300 °C were investigated by examining texture and microstructure evolution during uniaxial tension and compression tests. DRX refines microstructure at strains less than 0.2, and subsequently GBS plays a significant role during deformation process. A GBS model is developed to evaluate strain and grain rotation induced by GBS, and implemented into the polycrystal plasticity framework VPSC. The VPSC-DRX-GBS model can well reproduce the stress-strain curves, grain size, texture evolution and significant texture differences in tension and compression tests due to GBS. The calculated GBS contribution ratio in tension is obviously higher than that in compression due to easier cavity nucleation at grain boundaries under tension loading.
Key words: magnesium alloys; grain boundary sliding; dynamic recrystallization; polycrystal plasticity; texture
1 Introduction
Magnesium (Mg) alloys have attracted much attention due to their light mass potential especially in the transportation industry in the past two decades. Mg alloy sheets generally exhibit poor ductility at room temperature due to their hexagonal close packed (HCP) crystal structure with limited slip systems. Their ductility can be enhanced at high temperatures [1,2] which is partially attributed to the dynamic recrystallization (DRX) [3,4] and grain boundary sliding (GBS) [5-7].
Considerable efforts have been made to study the superplastic deformation of Mg alloys [8], where GBS acts as the key deformation mechanism [9-15]. SOMEKAWA et al [14] studied the stretch formability for the wrought processed pure magnesium, Mg-Mn alloy and AZ31 alloy, by using the Erichsen test with the crosshead speeds of 1×10-3 and 1×10-5 mm/s at room temperature. The stretch formability of pure magnesium was found to be improved with grain refinement, mainly due to the contribution of GBS. TAN and TAN [16] enhanced ductility of the AZ31 alloy sheet by two-stage deformation at 1×10-4 s-1. At the first stage, grains were refined through DRX at 250 °C; at the second stage, deformation was performed at a higher temperature to achieve a high elongation-to- failure through GBS of those refined equiaxed grains. KOIKE and OHYAMA [17] examined the rolled AZ31 alloy sheet by tensile testing at temperatures ranging from room temperature to 250 °C. The occurrence of GBS was characterized by the displacement of scribed lines across grain boundaries of deformed samples. BARNETT et al [18] conducted a series of tensile experiments for the hot-rolled AZ31 Mg alloy at different temperatures and concluded that the GBS can diminish plastic anisotropy rapidly with increasing temperatures.
The grain rotation induced by GBS, which does not follow the rotation rules as for dislocation slip, will not contribute to total strain but can provide an additional degree of freedom. GBS generally leads to reduction in texture intensity [6,16,19-21]. In uniaxial tension of the 5083 aluminum alloy with partially recrystallized grains of 9 μm size at 335-535 °C, the texture tends to be increasingly random due to GBS [22]. YANG et al [23] examined a fine-grained ZK60 Mg alloy in uniaxial tension along the longitudinal and transverse directions at 225-335 °C and 3×10-4 s-1. During GBS involved deformation above 250 °C, highly isotropic flow was found along the longitudinal and transverse directions. The initial basal texture was weakened during deformation, owing to GBS and the accompanying random grain rotation. PANICKER et al [24] conducted tensile experiments on a fine-grained AZ31 alloy at 400 °C and investigated the GBS behavior with an elongation to failure of 475% at 1×10-4 s-1 and non-GBS behavior with an elongation to failure of 160% at 1×10-2 s-1. In the non-GBS deformation, there was a significant sharpening in texture, while in GBS deformation, the initial basal texture became much less pronounced.
The methods developed for modeling GBS deformation mainly include the phenomeno- logical models [25-29], crystalline plasticity methods [30,31], first principles calculation [32], finite element analyses [33,34] and molecular dynamics simulations [35-38], etc. HAHN et al [28,29] developed a phenomenological equation, which took the parameters of long-range threshold stresses, grain size, Boltzmann constant, absolute temperature, thermal vibration frequency, activation energy, etc. into consideration to determine the critical stress needed for mesoscopic grain boundary sliding of the nanocrystalline TiAl and ceramics. ZHU et al [35] used a polycrystalline constitutive model developed by ASARO et al [39] for describing deformation mechanisms in nanocrystalline metals and the extended aggregate Taylor model developed by ASARO and NEEDLEMAN [40], and analyzed the transition from dislocations-based deformation to GBS. They concluded that GBS starts contribution to deformation at the grain size below 15 nm. OVID’KO and SHEINERMAN [41] simulated the GBS and grain rotations in nanocrystalline nickel, which is realized via diffusion controlled climb of grain boundary dislocations, by using the dislocation dynamics approach. ALABORT et al [33] identified the GBS in the Ti-6Al-4V alloy at temperatures from 850 to 900 °C and strain rates between 0.001 and 0.0001 s-1, and proposed a unified visco-plastic model considering GBS in superplastic flow rate. The deformation map for the alloy was determined with the dominant deformation modes at different temperatures and strain rates. DOQUET and BARKIA [42] conducted crystal viscoplasticity finite element simulations based on real microstructure to compute the shear stress along the grain boundaries during tension of titanium at room temperature and various strain rates. The computations showed that sliding grain boundaries actually underwent higher shear stress than the average.
According to previous experimental research, the GBS involved deformation of Mg alloys is usually accompanied by DRX and includes two stages. In the early stage, the deformation is mainly accommodated by dislocation slip and DRX, through which the grains are refined; in the second stage, GBS plays an important or even dominant role by taking advantage of the already refined grains [16,24]. It is of great interest to develop a modeling method to incorporate the three mechanisms, thereby realizing the integrated simulation of texture evolution and mechanical response in GBS deformation of Mg alloys.
The aim of the present work is to develop a crystal plasticity modeling approach to integrate slip, DRX and GBS for simulating the deformation and texture evolution of Mg alloys deformed at high temperatures. Firstly, the deformation mechanisms of the AZ31B alloy sheet during uniaxial tension along rolling direction (RD tension), compression along RD (RD compression) and normal direction (ND compression) at 300 °C were studied by using optical microscopy (OM), X-ray diffractometry (XRD) and electron backscattered diffractometry (EBSD). The evolution of texture and microstructures under GBS involved deformation was examined. Furthermore, a GBS model was developed to describe GBS strain and grain rotation, and implemented into a visco-plastic self-consistent (VPSC) method. Finally, the deformation and texture evolution were numerically investigated.
2 Experimental
2.1 Experiment procedure
A commercial AZ31B-H24 alloy sheet was used in the present work, which was previously studied by ZHOU et al [43,44]. Before experiments, the sheets were annealed at 300 °C for 15 min, followed by furnace cooling to room temperature. The uniaxial tension and compression tests at 300 °C along rolling direction (RD) at a strain rate of 0.0018 s-1, uniaxial compression along the normal direction (ND) at 0.001 s-1, as well as subsequent OM and XRD observation have been introduced in detail elsewhere [44]. In the present work, additional OM, XRD and EBSD tests were carried out to further investigate the evolution of microstructure and texture.
The samples were cut into small pieces and mounted with resin, ground, polished using 3 and 1 μm diamond suspension, and then etched in a solution of 2.1 g picric acid, 5 mL acetic acid and 80 mL ethanol for about 5 s. The EBSD samples were prepared by using the triple ion beam milling system, Leica Em TIC 3X. Samples were installed on the platform at an angle of 10.5° and milled with the voltage of 5 keV for 20 min firstly, then platform angle of 4.5° was used with the voltage of 4.5 keV for 45 min and 3.5 keV for 30 min. NOVA Nano SEM 230 with Aztec HKL Max System was adopted for EBSD collection and analysis. The EBSD scanning area for each loading mode contained at least 200 grains.
2.2 Deformation mechanisms
Figure 1 shows the deformed and initial samples of RD tension, and the initial state of the sample. The original AZ31B sheet is mainly composed of equiaxed grain, with a strong initial ellipsoidal basal texture, and the sample of RD tension can deform to a large strain prior to fracture. To understand the deformation mechanism of RD tension at 300 °C, microstructures and textures were examined for the deformed samples at strains of 0.02, 0.05, 0.1, 0.15, 0.4 and 0.7.

Fig. 1 Initial and deformed samples of RD tension (a), optical micrograph of initial sample (b) and macro texture from XRD of initial sample (c)
Figure 2 shows the inverse pole figures (IPFs) map and textures from EBSD at strains of 0.02-0.15, and OM results at strains of 0.4 and 0.7. The corresponding grain size distributions are shown in Fig. 3. At a strain of 0.02, the grain size of 6-9 μm accounts for the largest number fraction, followed by 3-6 μm and 9-12 μm. The grain size distribution is slightly different from the initial microstructure shown in Fig. 1, where many large grains with the size over 21 μm can be found. Due to holding before tension at 300 °C, the grain size slightly increases. A strong ellipsoidal basal texture exists at a strain of 0.02 where the c-axis of grains tilts slightly away from the normal and towards the rolling direction, while the intensity distribution of 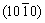 planes is remarkably diffused.
planes is remarkably diffused.

Fig. 2 IPF maps, OM images, and textures under RD tension at 300 °C and different strains (The OM results at strains of 0.4 and 0.7 were taken from the work of ZHOU et al [44])

Fig. 3 Grain size distributions under RD tension at 300 °C and different strains
At a strain of 0.05, the grains with the size of 3-6 μm increase gradually, while the grains over 21 μm decrease. As the strain increases from 0.02 to 0.05, the large grains are preferentially recrystallized, leading to the generation of small DRX grains; the maximum texture intensities in (0002) pole figures (PFs) decreases from 7.0 to 6.4, and the hexagonal maxima distribution in 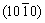 PFs is looming.
PFs is looming.
At a strain of 0.1, numerous small grains with size under 3 μm come into being, and the grains with size over 18 μm are consumed by the small grains. From the change in microstructure at strains from 0.05 to 0.1, the occurrence of DRX can be justified. During the DRX process, a more dispersed texture of new DRX grains, which can be regarded as random misorientation of 15° with their parent grains, will lower the texture intensity [43]. Due to the orientation randomization effect induced by DRX, the texture distribution in 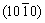 PFs at a strain of 0.1 is considerably more diffused than that at a strain of 0.05. The hexagonal maxima distribution of
PFs at a strain of 0.1 is considerably more diffused than that at a strain of 0.05. The hexagonal maxima distribution of  planes at a strain of 0.1 is not further enhanced with straining, and maximum texture intensity in (0002) PFs decreases to 5.6.
planes at a strain of 0.1 is not further enhanced with straining, and maximum texture intensity in (0002) PFs decreases to 5.6.
At a strain of 0.15, the number of small grains with size below 3 μm decreases, while the number of grains with the size of 3-9 μm increases. This is related to the discontinuous dynamic recrystallization (DDRX), during which small DRX grains nucleate and then grow up through grain boundary migration. The DDRX turns to be attenuated at strains higher than 0.1 and few new DRX grains appear. Evident hexagonal maxima distribution of  planes is gradually developed, while the maximum texture intensity in (0002) PFs increases to 8.4 at a strain of 0.15. With the DDRX attenuated, the texture intensities are enhanced again, leading to the appearance of hexagonal maxima distribution.
planes is gradually developed, while the maximum texture intensity in (0002) PFs increases to 8.4 at a strain of 0.15. With the DDRX attenuated, the texture intensities are enhanced again, leading to the appearance of hexagonal maxima distribution.
The number of small grains with the size under 3 μm decreases gradually until a strain of 0.4, and the grains with the size of 3-9 μm owns most of the number fraction. At a strain of 0.7, the grain size distribution and grain configurations, are similar to those at a strain of 0.4, and the number of grains with the size of 3-9 μm keeps nearly constant. It can be concluded that DRX falls into being less activated at a strain of 0.15 and no longer occurs at a strain of 0.4, corresponding to the stable distribution of grain size and texture.
The (0002) and 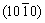 PFs from XRD examination in RD tension at 300 °C and strains of 0.4 and 0.7 are also presented in Fig. 2. In (0002) PF, with the increase of strain from 0.4 to 0.7, the original tilted basal texture exhibits a single peak and a slight increment in intensity. In
PFs from XRD examination in RD tension at 300 °C and strains of 0.4 and 0.7 are also presented in Fig. 2. In (0002) PF, with the increase of strain from 0.4 to 0.7, the original tilted basal texture exhibits a single peak and a slight increment in intensity. In 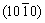 PF, a ring-shaped texture is formed at these two strains, whereas the hexagonal maxima distribution, which is typically developed in RD tension of Mg alloys, no longer exists. In contrast, the obvious hexagonal maxima distribution of
PF, a ring-shaped texture is formed at these two strains, whereas the hexagonal maxima distribution, which is typically developed in RD tension of Mg alloys, no longer exists. In contrast, the obvious hexagonal maxima distribution of  planes can be found in the present AZ31B sheet at strains of 0.4 and 0.7 when the alloy is deformed at the temperatures of 100 and 200 °C, due to the activity of prismatic slip [44]. The difference between texture development at 300 °C and lower temperatures is attributed to different deformation mechanisms accommodating plastic deformation in RD tension.
planes can be found in the present AZ31B sheet at strains of 0.4 and 0.7 when the alloy is deformed at the temperatures of 100 and 200 °C, due to the activity of prismatic slip [44]. The difference between texture development at 300 °C and lower temperatures is attributed to different deformation mechanisms accommodating plastic deformation in RD tension.
GBS takes effect as a key deformation mechanism at high temperatures, especially for alloys with refined microstructure. As explained by MCNELLEY et al [21] and PANICKER et al [24], the texture becomes more random and the grain size keeps constant under GBS deformation in RD tension. Therefore, the hexagonal maxima distribution in RD tension disappears at 300 °C due to texture randomization induced by GBS. At strains less than 0.4, prismatic slip rotates the grain around the c-axis to a particular balance position during the plastic deformation [44], which forms the hexagonal maxima distribution of  planes. However, when GBS takes effect, the grain will rotate around c-axis by a random angle, and there is no specific balance direction, leading to the ring-shaped texture at strains of 0.4 and 0.7. Moreover, the sample can be stretched up to elongation of 159% before fracture, and stress is softened at strains higher than 0.2 [44], which also corresponds to typical GBS activities. In contrast, the elongations are only 80% at 200 °C and 65% at 150 °C, respectively.
planes. However, when GBS takes effect, the grain will rotate around c-axis by a random angle, and there is no specific balance direction, leading to the ring-shaped texture at strains of 0.4 and 0.7. Moreover, the sample can be stretched up to elongation of 159% before fracture, and stress is softened at strains higher than 0.2 [44], which also corresponds to typical GBS activities. In contrast, the elongations are only 80% at 200 °C and 65% at 150 °C, respectively.
In summary, in RD tension at 300 °C, DDRX is initiated at small strains, characterized by nucleation and subsequent growth of DRX grains; as DDRX turns to be attenuated, GBS plays a significant role in large deformation, resulting in more random texture. The present results show similar trends as the tensile experiments of AZ31 sheets with initial grain size of 12 μm, at 250 °C and a strain rate of 10-4 s-1 [16], and with initial grain size of 300 μm, at 500 °C and a strain rate of 10-3 s-1 [45]. In both of these researches, the involved deformation mechanisms also include grain refinement stage and GBS deformation stage.
2.3 Difference in tension and compression due to GBS
The OM microstructures under RD compression at strains of 0.2 and 0.4 are shown in Fig. 4, and the corresponding grain size distributions are shown in Fig. 5. The grain size distribution for RD compression keeps stable with the strain change, similar to that for RD tension at a strain of 0.4, i.e. the grains with the size of 3-6 μm take the largest number fraction, followed by 6-9 μm size. The OM results under ND compression at a strain of 0.4, as shown in Fig. 6, and corresponding grain size distributions shown in Fig. 7, show no evident difference from RD compression. In fact, except for the subtle difference in the mean grain size, the grain size distribution and its evolution with strain change little with respect to loading mode. From the OM results, the DRX phenomenon is not observed at strains higher than 0.2.
The (0002) and 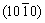 PFs under uniaxial compression along RD and ND at 300 °C are shown in Figs. 4 and 6, respectively. Compared with the initial texture, a gradually split basal texture is developed, which moves from the center to the RD poles in (0002) PF for RD compression, and two diffuse maxima appear at the TD poles in
PFs under uniaxial compression along RD and ND at 300 °C are shown in Figs. 4 and 6, respectively. Compared with the initial texture, a gradually split basal texture is developed, which moves from the center to the RD poles in (0002) PF for RD compression, and two diffuse maxima appear at the TD poles in 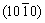 PF. For ND compression, the initial texture and deformed texture are different only in density.
PF. For ND compression, the initial texture and deformed texture are different only in density.
The texture distributions under RD and ND compression at 300 °C are similar to those at 200 °C [44]. RD tension and RD/ND compression at 300 °C show obvious tension-compression difference in terms of texture development. Generally, GBS induced deformation in tension is obviously larger than that in compression. For example, in the creep test of AE42 magnesium alloy under the constant stress of 75 MPa at 175 °C, the creep strain in tension can be up to about 2.4 times of compression creep rate [46]. During the room temperature creep of Ti-6242 titanium alloy under 931 MPa stress, the largest ratio of tension creep strain to compression creep strain even reached 6.7 within 150 h [47]. The texture developed in RD/ND compression at 300 °C, which is similar to that at 200 °C, can be attributed to less activation of GBS in compression.

Fig. 4 OM images and textures under RD compression at 300 °C and strains of 0.2 and 0.4

Fig. 5 Grain size distributions under RD compression at 300 °C and strains of 0.2 (a) and 0.4 (b)

Fig. 6 OM image (a) and texture (b) under ND compression at 300 °C and strain of 0.4

Fig. 7 Grain size distributions under ND compression at 300 °C and strain of 0.4
From the experimental results mentioned above, a strain of 0.2 is determined as the transition point between DRX and GBS mechanisms for the present alloy.
3 Polycrystal plasticity modeling
In this section, DRX and GBS mechanisms are incorporated into the VPSC framework [43,48] to develop a polycrystal plasticity based method for simulating the deformation of the AZ31B sheet at 300 °C.
3.1 VPSC model with dislocation density based hardening law
In the VPSC framework, each grain is treated as an ellipsoidal visco-plastic inclusion embedded in an effective visco-plastic medium [49]. In each grain, the shear strain rate of each slip system 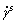 follows the power law as
follows the power law as
 (1)
(1)
where 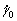 is the reference strain rate, equal to the macroscopic strain rate, m is the rate sensitivity parameter obtained from the experiment [44], σ:Ps is the resolved shear stress, and
is the reference strain rate, equal to the macroscopic strain rate, m is the rate sensitivity parameter obtained from the experiment [44], σ:Ps is the resolved shear stress, and  is the critical resolved shear stress (CRSS).
is the critical resolved shear stress (CRSS).
A simplified equation for calculating CRSS on slip system is employed [43,50-52], where the contributions of debris and grain size effect are omitted.
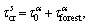 s∈α (2)
s∈α (2)
where  is the initial critical shear stress on the slip, and α is the silp mode. The forest hardening
is the initial critical shear stress on the slip, and α is the silp mode. The forest hardening  is calculated by the Taylor law:
is calculated by the Taylor law:
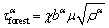 (3)
(3)
where χ is the dislocation interaction coefficient, and χ=0.9 [47,49], bα is the magnitude of the Burgers vector associated with the slip mode, μ is the shear module, and ρ is the dislocation density.
Dislocation density ρ is thermally-controlled and updated based on dislocation generation and annihilation [53,54]:
 (4)
(4)
where  is a material constant,
is a material constant,  represents the rate coefficient for dynamic recovery by thermally activated mechanisms,
represents the rate coefficient for dynamic recovery by thermally activated mechanisms,  is the strain rate and T is the temperature.
is the strain rate and T is the temperature.
The deformation modes considered in the present modeling are basal  , prismatic
, prismatic  [52-56], and pyramidal-II
[52-56], and pyramidal-II  . Twinning is not active at the temperature of 300 °C and therefore not included in modeling.
. Twinning is not active at the temperature of 300 °C and therefore not included in modeling.
3.2 DRX nucleation and grain growth
For a polycrystal with multiple slip systems, when the total dislocation density of grain i reaches a critical value ρc, new DRX grains will possibly nucleate. The expectation of DRX grain nucleation can be evaluated by [48]
 (5)
(5)
where N is the number of DRX grain nucleation,  is the nucleation rate, K is the number of grains with ρi>ρc, C(T) is a function of temperature, Si is the surface area of grain i, and Δt is the time increment of a simulation step.
is the nucleation rate, K is the number of grains with ρi>ρc, C(T) is a function of temperature, Si is the surface area of grain i, and Δt is the time increment of a simulation step.
The grain boundary velocity Vi is assumed to be proportional to the stored energy difference across the boundary and calculated by [57]
 (6)
(6)
where M(T) is the grain boundary mobility related to temperature,  is the average dislocation density, ρi is the dislocation density of grain i, WGT(i) is the volume weight of grain i, and τ is the dislocation line energy [58]
is the average dislocation density, ρi is the dislocation density of grain i, WGT(i) is the volume weight of grain i, and τ is the dislocation line energy [58]
 (7)
(7)
where nslip is the total number of slop modes.
3.3 GBS strain rate
The total strain rate is composed of strain rates induced by both dislocation slip and GBS [22,35,59], i.e.
 (8)
(8)
where  and
and 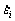 represent strain rates of grain i due to GBS and dislocation slip, respectively. GBS strain rate can be generally expressed as a function of temperature, grain size and applied stress [6,59-61]. A model originally proposed by CONRAD and NARARYAN [25] and further updated by ZHU et al [35] and WEI and GAO [31] is employed for calculating strain rate of each grain:
represent strain rates of grain i due to GBS and dislocation slip, respectively. GBS strain rate can be generally expressed as a function of temperature, grain size and applied stress [6,59-61]. A model originally proposed by CONRAD and NARARYAN [25] and further updated by ZHU et al [35] and WEI and GAO [31] is employed for calculating strain rate of each grain:
 (9)
(9)
where υD is a typical lattice vibrational frequency, and υD≈1013 s-1; di is the grain size; V is the activation volume, taken as  [25,35]; σi is the effective stress of grain i; KB is the Boltzmann constant (1.38×10-23 J/K); T is the temperature; ΔF is the activation energy for grain boundary diffusion (92 kJ/mol for Mg alloys) [62]; R is the molar gas constant (8.314 J/(mol·K)).
[25,35]; σi is the effective stress of grain i; KB is the Boltzmann constant (1.38×10-23 J/K); T is the temperature; ΔF is the activation energy for grain boundary diffusion (92 kJ/mol for Mg alloys) [62]; R is the molar gas constant (8.314 J/(mol·K)).
The cavitation damage parameter Dc is introduced to characterize the process of void nucleation, growth and coalescence during high temperature deformation [63]. For grain i, Dc,i is determined by the rupture strain εf and GBS strain rate as fallows, considering the difference in tension and compression.
 (10)
(10)
where Dc,i is permanently set to zero in compression and the hydrostatic pressure σm,i=1/3(σ1,i+σ2,i+σ3,i).
3.4 Grain rotation mediated by GBS
In the GBS regime [21], initial basal texture of the rolled and annealed magnesium alloys become more random with the increase of deformation, and strain rate and GBS contribution are critical factors for grain rotation [24]. In the present work, a model to introduce GBS induced grain rotation is proposed as follows.
When GBS takes effect, grains affected by GBS are randomly selected to rotate in addition to the rotation induced by dislocation slip. The number of the picked grains is proportional to the ratio of GBS strain rate to total strain rate. Therefore, the expectation of rotated grains zGBS is determined by
 (11)
(11)
where hg is the fitting parameter; ng is the total grain number; ξGBS,i is the GBS contribution ratio for grain i.
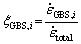 (12)
(12)
The extra random rotation degree of each selected grain should be within 45° [6].
Under GBS dominated deformation, the compatible conditions (five slip systems needed for compatible and homogeneous deformation under plastic deformation) are not necessary to be fulfilled, and grain rotation will randomize the deformation texture [22,24]. In uniaxial tension of the present AZ31B sheet, the c-axis rotates toward the sheet normal by basal slip, while prismatic slip rotates the grain around c-axis to the balance position. After the onset of GBS, the grain rotates about c-axis by a random angle with no specific balance direction, as explained in Section 2.2.
3.5 VPSC-DRX-GBS integrated model
The above DRX and GBS methods are implemented into the VPSC framework. Figure 8 shows the flowchart of the proposed VPSC-DRX- GBS approach. The computational procedures are as follows.
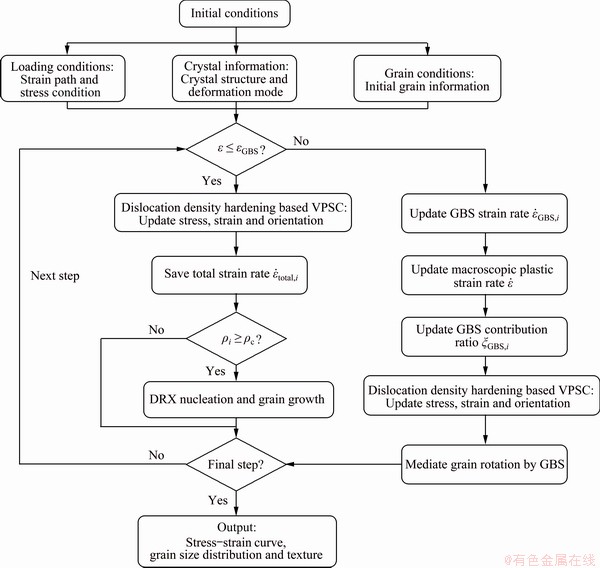
Fig. 8 Flowchart of VPSC-DRX-GBS model
(1) If the strain is less than the critical value for initiating GBS, eGBS, the status of a given aggregate, including stress, strain and orientation, is updated by the VPSC model, and the total strain rate 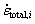 for grain i is equal to the plastic strain rate
for grain i is equal to the plastic strain rate 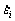 .
.
(2) When the critical dislocation density for DDRX initiation is achieved, new DRX grains will nucleate, according to Eq. (5), followed by growth through boundary migration described with Eq. (6).
(3) If the strain reaches eGBS, the GBS strain rate for each grain i is calculated by using Eq. (9), and the direction of GBS strain rate is assumed to be parallel to the direction of plastic strain rate 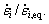
(4) Update the macroscopic plastic strain rate  in which the weighted average of the plastic strain rate over the aggregate has to coincide with the macroscopic counterpart [64], i.e.
in which the weighted average of the plastic strain rate over the aggregate has to coincide with the macroscopic counterpart [64], i.e.
 (13)
(13)
where the bracket “<>” denotes the average over grains, weighted by associated volume fractions.
(5) Calculate stress and strain by using the macroscopic plastic strain rate in the framework of VPSC, and update effective stress σi for grains.
(6) Calculate rotation of grains by Eqs. (11) and (12).
3.6 Modeling of AZ31B sheet
In the present work, the experimental results in the work of ZHOU et al [44] on the same AZ31B sheet subjected to RD tension, RD compression and ND compression at 300 °C and strain rate of 1×10-3 s-1 are used for calibration of the modeling parameters, since the same material is studied here. The input parameters of the VPSC-DRX-GBS modeling are as follows.
The initial average grain size at 300 °C is 8 μm from Fig. 3 (Due to the holding at higher temperature, the grain size slightly increases. Therefore, the initial grain size at 300 °C is set to be 8 μm, instead of 7 μm [43,48]), and initial grain number is 300. The initial grain orientations are given according to the initial texture. The shear modulus m at 300 °C is taken as 14000 MPa [62]. The meff homogenization method in framework VPSC with meff=5 is adopted in simulation process [43,48,55]. According to the EBSD observation, the size of newly generated DDRX grains is assumed to be 1.5 μm. The new grains are assumed to share the same c-axis with their parent grains, and the misorientation angle between each DRX grain and its parent grain, due to the rotation of basal plane, follows the Gaussian distribution with the mean value of 15° and standard deviation of 15° [43].
The hardening and DRX parameters are listed in Table 1. The hardening parameters (τ0, k1 and k2 in Table 1) are determined by fitting both the hardening curves and r values (r represents the plastic anisotropy of a rolled sheet) [44] up to the peak stresses. Considering various deformation mechanisms activated at different deformation stages [43], firstly the hardening parameters, τ0, k1 and k2, for basal and prismatic slip modes are determined by fitting RD tension and RD compression experimental results (stress-strain curves and r value) prior to stress softening, without incorporating DRX and GBS modules; similarly, the ND compression experimental results are used to determine hardening parameters for
4 Simulation results and discussion
4.1 Flow stress
Figure 9 shows the comparison between the experimental and fitted stress-strain curves and variation of r value. The calculated results by the VPSC-DRX-GBS model agree well with the experimental results of RD tension, RD compression and ND compression. For comparison, the stress-strain curves without considering GBS are also calculated and shown in Fig. 9(a), by using the same hardening parameters but turning the GBS module off. Without consideration of GBS, the calculation obviously overestimates the stress at strains higher than 0.2, and cannot reproduce the softening behavior. GBS gives rise to more softening in tension than in compression, because contribution of GBS to deformation is significantly reduced in compression.
Table 1 VPSC-DRX-GBS modeling parameters of AZ31B sheet
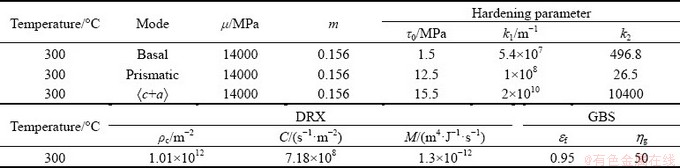

Fig. 9 Experimental and fitted results of AZ31B sheets at 300 °C
4.2 Grain size evolution
Figure 10 shows the calculated average grain size varying with true strain under three loading conditions, and comparison with measured results obtained by OM and EBSD observation. The calculated results are consistent with the experimental ones. The average grain size decreases from initial 8 to 7 μm in RD tension, to 6.5 μm in RD compression and to 6.9 μm in ND compression at a strain of 0.2. It decreases gradually at strains less than 0.2 due to DRX, and keeps constant at strains higher than 0.2.
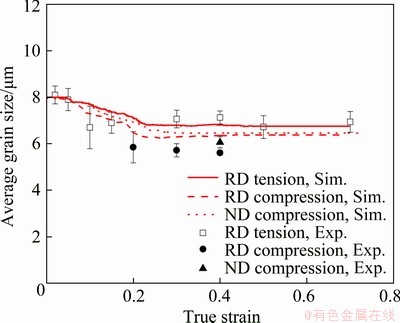
Fig. 10 Evolution of average grain size with change of strain at 300 °C
4.3 Texture
The calculated texture at a strain of 0.4 in the form of pole figures is compared with experimental results under three loading conditions, as shown in Fig. 11. The predicted texture in RD tension considering GBS is consistent with measurements, and texture intensity with GBS module is reduced compared to that without considering GBS. In RD tension, the dominantly active basal and prismatic slip modes cause the suppression of basal texture in the (0002) pole figure and the formation of hexagonal maxima distribution in the 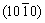 pole figure. With the enhancement of GBS, random rotation of grains reduces overall texture intensity, which results in more disperse distribution texture in the (0002) pole figure, and the hexagonal maxima distribution disappears.
pole figure. With the enhancement of GBS, random rotation of grains reduces overall texture intensity, which results in more disperse distribution texture in the (0002) pole figure, and the hexagonal maxima distribution disappears.
In compression, the texture distributions with and without considering GBS are similar due to less activation of GBS. In RD compression, the activation of the basal slip and prismatic slip modes splits the basal texture in the (0002) pole figure and results in two maxima distributions in the 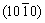 pole figure [43]. In ND compression, the basal texture in the (0002) pole figure is enhanced by active basal and pyramidal-II
pole figure [43]. In ND compression, the basal texture in the (0002) pole figure is enhanced by active basal and pyramidal-II 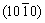 pole figure.
pole figure.
Figure 12 shows the predicted texture evolution with tensile strain. The hexagonal maxima distribution of  planes is gradually developed before at strains higher than 0.2, and due to the occurrence of DRX, the maximum texture intensity slightly fluctuates between 5.2 and 5.3 at strains from 0.05 to 0.2. At strains higher than 0.2, the ring-shaped texture replaces hexagonal maxima distribution due to the grain rotation induced by GBS.
planes is gradually developed before at strains higher than 0.2, and due to the occurrence of DRX, the maximum texture intensity slightly fluctuates between 5.2 and 5.3 at strains from 0.05 to 0.2. At strains higher than 0.2, the ring-shaped texture replaces hexagonal maxima distribution due to the grain rotation induced by GBS.
4.4 GBS contribution
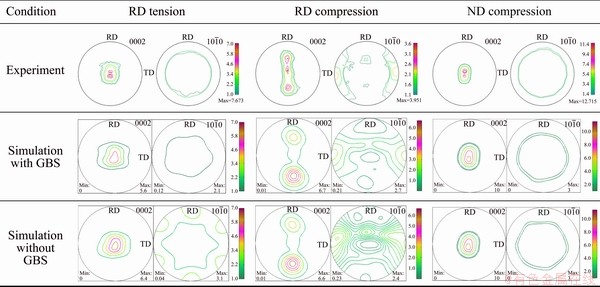
Fig. 11 Comparison of textures between simulation and experiment at strain of 0.4

Fig. 12 Predicted texture evolution under RD tension at different strains
The calculated average GBS contribution ratios 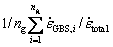 under RD tension, RD compression and ND compression, with the proceeding of deformation at strains higher than 0.2, are presented in Fig. 13. The GBS contribution that in RD tension is obviously higher than ratio in RD compression and ND compression. The evolution trends of GBS contribution ratio vary with the loading modes. For RD tension, the GBS contribution ratio rises steadily, with increasing cavitation damage parameter Dc and strain. For RD and ND compression, the GBS contribution ratio decreases slowly from 0.16 to 0.14 and from 0.18 to 0.165, respectively, as the true strain increases from 0.2 to 0.6, resulting from the stress softening. The significant reduction of the GBS contribution ratio in the compression mode, from the experiments conducted by DIERINGA et al [46] and LI et al [65], is confirmed by the current VPSC-DRX-GBS model. A much higher tension GBS contribution ratio than compression GBS contribution ratio has been reported for the aluminum alloys [65,66] and was attributed to the easier cavity nucleation at grain boundaries under tensile creep condition.
under RD tension, RD compression and ND compression, with the proceeding of deformation at strains higher than 0.2, are presented in Fig. 13. The GBS contribution that in RD tension is obviously higher than ratio in RD compression and ND compression. The evolution trends of GBS contribution ratio vary with the loading modes. For RD tension, the GBS contribution ratio rises steadily, with increasing cavitation damage parameter Dc and strain. For RD and ND compression, the GBS contribution ratio decreases slowly from 0.16 to 0.14 and from 0.18 to 0.165, respectively, as the true strain increases from 0.2 to 0.6, resulting from the stress softening. The significant reduction of the GBS contribution ratio in the compression mode, from the experiments conducted by DIERINGA et al [46] and LI et al [65], is confirmed by the current VPSC-DRX-GBS model. A much higher tension GBS contribution ratio than compression GBS contribution ratio has been reported for the aluminum alloys [65,66] and was attributed to the easier cavity nucleation at grain boundaries under tensile creep condition.

Fig. 13 Evolution of average GBS contribution ratio to overall strain rate at 300 °C
4.5 Slip activities
The relative slip activities of different slip modes in RD tension, RD and ND compression with and without considering the GBS effect are presented in Fig. 14. For each loading condition, when the strain is less than 0.2, the slip activities for different slip modes with consideration of GBS are similar to those without incorporating the GBS module. Thereafter, the slip activities with and without considering GBS mechanism gradually turn to be obviously different.
Basal slip is the dominant slip mode under all the loading conditions, with an increasing trend of activity for RD tension/compression and a decreasing trend for ND compression with deformation. In RD tension, prismatic slip mode accounts for most of other slip activities. After GBS takes effect, basal slip activity increases dramatically, while prismatic slip decreases correspondingly. In RD compression, prismatic slip with a decreasing trend of relative activity acts as a secondary mode at first, and

Fig. 14 Predicted slip activities at 300 °C
According to the above analysis, GBS mainly enhances the basal slip mode. GBS comes into being at strains higher than 0.2, which enhances the activity for basal slip more effectively for RD tension than for RD/ND compression. In order to explain the evidently enhanced basal slip, the relative activities of different slip modes in RD tension are calculated by removing the effect of texture randomization (keeping orientations of DRX grains the same as their parent grains, and setting the GBS-induced grain rotation as zero), as shown in Fig. 15. If excluding the effect of texture randomization, the relative activity of basal slip decreases to the level without GBS or even lower at strains higher than 0.42. The prismatic slip without the effect of texture randomization becomes more obvious than that without GBS because the plastic strain rate is reduced by GBS and the prismatic slip is preferred at higher strain rates [67]. Therefore, the effect of texture randomization induced by DRX and GBS can explain the enhanced basal slip and less activated hard slip modes.

Fig. 15 Comparison of predicted slip activities at 300 °C for RD tension, including with/without considering GBS and removing effect of texture randomization
5 Conclusions
(1) The deformation of the AZ31B sheet experiences DRX at strains higher than 0.2, which leads to refined grains.
(2) A polycrystal plasticity based integration modeling method incorporating both DRX and GBS is developed, and the stress-strain curves, grain size evolution, texture evolution and slip activity can be simultaneously calculated.
(3) By introducing the cavitation damage parameter Dc into GBS model, the polycrystal plasticity model can reproduce the tension- compression difference induced by GBS.
(4) Due to GBS, tension deformation and compression deformation result in significant different texture development. In RD tension, the random grain rotation induced by GBS produces more dispersed distribution textures in the (0002) pole figure, and hexagonal maxima distribution of  planes disappears. In the compression modes, GBS effect is much weaker, which hardly influences texture distribution. The proposed model for GBS mediated grain rotation can well reproduce the measured texture development.
planes disappears. In the compression modes, GBS effect is much weaker, which hardly influences texture distribution. The proposed model for GBS mediated grain rotation can well reproduce the measured texture development.
(5) GBS enhances the activity of basal slip more obviously for RD tension than for RD and ND compression due to the effect of texture randomization.
Acknowledgments
The authors would like to acknowledge the support from the National Natural Science Foundation of China (51675331 and 51775337), Major Projects of the Ministry of Education (311017). Pei-dong WU would like to acknowledge the support from the Natural Sciences and Engineering Research Council of Canada (NSERC, RGPIN-2016-06464).
References
[1] CAO X Q, XU P P, FAN Q, WANG W X. Theoretical prediction of forming limit diagram of AZ31 magnesium alloy sheet at warm temperatures [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(9): 2426-2432.
[2] AYER O. A forming load analysis for extrusion process of AZ31 magnesium [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(4): 741-753.
[3] YIN D L, ZHANG K F, WANG G F, HAN W B. Warm deformation behavior of hot-rolled AZ31 Mg alloy [J]. Materials Science and Engineering A, 2005, 392: 320-325.
[4] DEL VALLE J A, RUANO O A. Influence of texture on dynamic recrystallization and deformation mechanisms in rolled or ECAPed AZ31 magnesium alloy [J]. Materials Science and Engineering A, 2008, 487: 473-480.
[5] QIAO Y D, WANG X, LIU Z Y, WANG E. Effect of temperature on microstructures, texture and mechanical properties of hot rolled pure magnesium sheets [J]. Materials Science and Engineering A, 2013, 568: 202-205.
[6] CHOKSHI A H, MUKHERJEE A K, LANGDON T G. Superplasticity in advanced materials [J]. Materials Science and Engineering R, 1993, 10: 237-274.
[7] BERGE F, KRüGER L, OUAZIZ H, ULLRICH C. Influence of temperature and strain rate on flow stress behavior of twin-roll cast, rolled and heat-treated AZ31 magnesium alloys [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 1-13.
[8] CAO F R, ZHOU B J, YIN B, XUE G Q, ZHU X T, XU G M. Modeling of deformation energy at elevated temperatures and its application in Mg-Li-Al-Y alloy [J]. Transactions of Nonferrous Metals Society of China, 2017, 27(11): 2434-2442.
[9] WU Y P, XIONG H Q, JIA Y Z, XIE S H, LI G F. Microstructure, texture and mechanical properties of Mg-8Gd–4Y–1Nd–0.5Zr alloy prepared by pre-deformation annealing, hot compression and ageing [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(5): 976-983.
[10] QIAO J, BIAN F B, HE M, WANG Y. High temperature tensile deformation behavior of AZ80 magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(10): 2857-2862.
[11] ROODPOSHTI P S, SARKAR A, MURTY K L, BRODY H, SCATTERGOOD R. Grain boundary sliding mechanism during high temperature deformation of AZ31 magnesium alloy [J]. Materials Science and Engineering A, 2016, 669: 171-177.
[12] CHAI F, ZHANG D T, LI Y Y, ZHANG W W. High strain rate superplasticity of a fine-grained AZ91 magnesium alloy prepared by submerged friction stir processing [J]. Materials Science and Engineering A, 2013, 568: 40-48.
[13] WATANABE H, TSUTSUI H, MUKAI T, KOHZU M, TANABE S, HIGASHI K. Deformation mechanism in a coarse-grained Mg-Al-Zn alloy at elevated temperatures [J]. International Journal of Plasticity, 2001, 17: 387-397.
[14] SOMEKAWA H, KINOSHITA A, WASHIO K, KATO A. Enhancement of room temperature stretch formability via grain boundary sliding in magnesium alloy [J]. Materials Science and Engineering A, 2016, 676: 427-433.
[15] WATANABE H, MUKAI T, KOHZU M, TANABE S, HIGASHI K. Effect of temperature and grain size on the dominant diffusion process for superplastic flow in an AZ61 magnesium alloy [J]. Acta Materialia, 1999, 47: 3753-3758.
[16] TAN J C, TAN M J. Superplasticity and grain boundary sliding characteristics in two stage deformation of Mg-3Al-1Zn alloy sheet [J]. Materials Science and Engineering A, 2003, 339: 81-89.
[17] KOIKE J, OHYAMA R. Geometrical criterion for the activation of prismatic slip in AZ61 Mg alloy sheets deformed at room temperature [J]. Acta Materialia, 2005, 53: 1963-1972.
[18] BARNETT M R, GHADERI A, SABIROV I, HUTCHINSON B. Role of grain boundary sliding in the anisotropy of magnesium alloys [J]. Scripta Materialia, 2009, 61: 277-280.
[19] PEREZ-PRADO M T, MCNELLEY T R, SWISHER D L, GONZALEZ-DONCEL G, RUANO O A. Texture analysis of the transition from slip to grain boundary sliding in a continuously recrystallized superplastic aluminum alloy [J]. Materials Science and Engineering A, 2003, 342: 216-230.
[20] PEREZ-PRADO M T, CRISTINA M C, RUANO O A, GONZALEZ-DONCEL G. Grain boundary sliding and crystallographic slip during superplasticity of Al-5%Ca- 5%Zn as studied by texture analysis [J]. Materials Science and Engineering A, 1998, 244: 216-223.
[21] MCNELLEY T R, OH-ISHI K, ZHILYAEV A P, SWAMINATHAN S, KRAJEWSKI P E, TALEFF E M. Characteristics of the transition from grain-boundary sliding to solute drag creep in superplastic AA5083 [J]. Metallurgical and Materials Transactions A, 2008, 39: 50-64.
[22] PEREZ-PRADO M T, GONZALEZ-DONCEL G, RUANO O A, MCNELLEY T R. Texture analysis of the transition from slip to grain boundary sliding in a discontinuously recrystallized superplastic aluminum alloy [J]. Acta Materialia, 2001, 49: 2259-2268.
[23] YANG Q, FENG A H, XIAO B L, MA Z Y. Influence of texture on superplastic behavior of friction stir processed ZK60 magnesium alloy [J]. Materials Science and Engineering A, 2012, 556: 671-677.
[24] PANICKER R, CHOKSHI A H, MISHRA R K, VERMA R, KRAJEWSKI P E. Microstructural evolution and grain boundary sliding in a superplastic magnesium AZ31 alloy [J]. Acta Materialia, 2009, 57: 3683-3693.
[25] CONRAD H, NARAYAN J. On the grain size softening in nanocrystalline materials [J]. Scripta Materialia, 2000, 42: 1025-1030.
[26] FU H H, BENSON D J, MEYERS M A. Analytical and computational description of effect of grain size on yield stress of metals [J]. Acta Materialia, 2001, 49: 2567-2582.
[27] RAJ R, ASHBY M F. On grain boundary sliding and diffusional creep [J]. Metallurgical Transactions, 1971, 2: 1113-1127.
[28] HAHN H, MONDAL P, PADMANABHAN K A. Plastic deformation of nanocrystalline materials [J]. Nanostructured Materials, 1997, 9: 603-606.
[29] HAHN H, PADMANABHAN K A. A model for the deformation of nanocrystalline materials [J]. Philosophical Magazine B, 1997, 76: 559-571.
[30] SHI J, ZIKRY M A. Grain size, grain boundary sliding, and grain boundary interaction effects on nanocrystalline behavior [J]. Materials Science and Engineering A, 2009, 520: 121-133.
[31] WEI Y J, GAO H J. An elastic-viscoplastic model of deformation in nanocrystalline metals based on coupled mechanisms in grain boundaries and grain interiors [J]. Materials Science and Engineering A, 2008, 478: 16-25.
[32] SOMEKAWA H, TSURU T. Effect of alloying elements on grain boundary sliding in magnesium binary alloys: Experimental and numerical studies [J]. Materials Science and Engineering A, 2017, 708: 267-273.
[33] ALABORT E, PUTMAN D, REED R C. Superplasticity in Ti-6Al-4V: Characterisation, modelling and applications [J]. Acta Materialia, 2015, 95: 428-442.
[34] WARNER D H, SANSOZ F, MOLINARI J F. Atomistic based continuum investigation of plastic deformation in nanocrystalline copper [J]. International Journal of Plasticity, 2006, 22: 754-774.
[35] ZHU B, ASARO R J, KRYSL P, BAILEY R. Transition of deformation mechanisms and its connection to grain size distribution in nanocrystalline metals [J]. Acta Materialia, 2005, 53: 4825-4838.
[36] van SWYGENHOVEN H, DERLET P M. Grain-boundary sliding in nanocrystalline fcc metals [J]. Physical Review B, 2001, 64: 1-9.
[37] SCHIOTZ J, VEGGE T, DI TOLLA F D, JACOBSEN K W. Atomic-scale simulations of the mechanical deformation of nanocrystalline metals [J]. Physical Review B, 1999, 60: 11971-11983.
[38] HASNAOUI A, van SWYGENHOVEN H, DERLET P M. Dimples on nanocrystalline fracture surfaces as evidence for shear plane formation [J]. Science, 2003, 300: 1550-1552.
[39] ASARO R J, KRYSL P, KAD B. Deformation mechanism transitions in nanoscale fee metals [J]. Philosophical Magazine Letters, 2003, 83: 733-743.
[40] ASARO R J, NEEDLEMAN A. Overview no. 42 Texture development and strain hardening in rate dependent polycrystals [J]. Acta Metallurgica, 1985, 33: 923-953.
[41] OVID’KO I A, SHEINERMAN A G. Kinetics of grain boundary sliding and rotational deformation in nanocrystalline materials [J]. Reviews on Advanced Materials Science, 2013, 35: 48-58.
[42] DOQUET V, BARKIA B. Combined AFM, SEM and crystal plasticity analysis of grain boundary sliding in titanium at room temperature [J]. Mechanics of Materials, 2016, 103: 18-27.
[43] ZHOU G E, LI Z H, LI D Y, PENG Y H, WANG H M, WU P F. Misorientation development in continuous dynamic recrystallization of AZ31B alloy sheet and polycrystal plasticity simulation [J]. Materials Science and Engineering A, 2018, 730: 438-456.
[44] ZHOU G W, JAIN M K, WU P D, SHAO Y C, LI D Y, PENG Y H. Experiment and crystal plasticity analysis on plastic deformation of AZ31B Mg alloy sheet under intermediate temperatures: How deformation mechanisms evolve [J]. International Journal of Plasticity, 2016, 79: 19-47.
[45] WU X, LIU Y. Superplasticity of coarse-grained magnesium alloy [J]. Scripta Materialia, 2002, 46: 269-274.
[46] DIERINGA H, HORT N, KAINER K U. Investigation of minimum creep rates and stress exponents calculated from tensile and compressive creep data of magnesium alloy AE42 [J]. Materials Science and Engineering A, 2009, 510-511: 382-386.
[47] NEERAJ T, SAVAGE M F, TATALOVICH J, KOVARIK L, HAYES R W, MILLS M J. Observation of tension- compression asymmetry in α/β and titanium alloys [J]. Philosophical Magazine, 2005, 85: 279-295.
[48] ZHOU G W, LI Z H, LI D Y, PENG Y H, ZUROB H S, WU P D. A polycrystal plasticity based discontinuous dynamic recrystallization simulation method and its application to copper [J]. International Journal of Plasticity, 2017, 91: 48-76.
[49] LEBENSOHN R A, TOME C N. A self-consistent viscoplastic model: prediction of rolling textures of anisotropic polycrystals [J]. Materials Science and Engineering A, 1994, 175: 71-82.
[50] BEYERLEIN I J, TOME C N. A dislocation-based constitutive law for pure Zr including temperature effects [J]. International Journal of Plasticity, 2008, 24: 867-895.
[51] CAPOLUNGO L, BEYERLEIN I J, KASCHNER G C, TOME C N. On the interaction between slip dislocations and twins in HCP Zr [J]. Materials Science and Engineering A, 2009, 513-514: 42-51.
[52] OPPEDAL A L, EL KADIRI H, TOME C N, KASCHNER G C, VOGEL S C, BAIRD J C, HORSTEMEYER M F. Effect of dislocation transmutation on modeling hardening mechanisms by twinning in magnesium [J]. International Journal of Plasticity, 2012, 30-31: 41-61.
[53] MECKING H, KOCKS U F. Kinetics of flow and strain- hardening [J]. Acta Metallurgica, 1981, 29: 1865-1875.
[54] KOCKS U F, MECKING H. Physics and phenomenology of strainhardening: The FCC case [J]. Progress in Materials Science, 2003, 48: 171-273.
[55] WANG H M, RAEISINIA B, WU P D, AGNEW S R, TOME C N. Evaluation of self-consistent polycrystal plasticity models for magnesium alloy AZ31B sheet [J]. International Journal of Solids and Structures, 2010, 47: 2905-2917.
[56] JAIN A, AGNEW S R. Modeling the temperature dependent effect of twinning on the behavior of magnesium alloy AZ31B sheet [J]. Materials Science and Engineering A, 2007, 462: 29-36.
[57] CRAM D G, FANG X Y, ZUROB H S, BRECHET Y J M, HUTCHINSON C R. The effect of solute on discontinuous dynamic recrystallization [J]. Acta Materialia, 2012, 60: 6390-6404.
[58] DING R, GUO Z X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization [J]. Acta Materialia, 2001, 49: 3163-3175.
[59] LANGDON T G. Grain boundary sliding revisited: Developments in sliding over four decades [J]. Journal of Materials Science, 2006, 41: 597-609.
[60] KOIKE J, OHYAMA R, KOBAYASHI T, SUZUKI M, MARUYAMA K. Grain-boundary sliding in AZ31 magnesium alloys at room temperature to 523 K [J]. Materials Transactions, 2003, 44: 445-451.
[61] KOTTADA R S, CHOKSHI A H. Grain boundary sliding during diffusion and dislocation creep in a Mg-0.7PctAl alloy [J]. Metallurgical and Materials Transactions A, 2007, 38: 1743-1749.
[62] FROST H J, ASHBY M F. Deformation mechanism maps: the plasticity and creep of metals and ceramics [M]. Oxford: Pergamon Press, 1982.
[63] SONDHI S K, DYSON B F, MCLEAN M. Tension- compression creep asymmetry in a turbine disc superalloy: Roles of internal stress and thermal ageing [J]. Acta Materialia, 2004, 52: 1761-1772.
[64] LEBENSOHN R A, TOME C N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys [J]. Acta Metallurgica et Materialia, 1993, 41: 2611-2624.
[65] LI Y, SHI Z D, LIN J G, YANG Y L, RONG Q, HUANG B M, CHUNG T F, TSAO C S, YANG J R, BALINT D S. A unified constitutive model for asymmetric tension and compression creep-ageing behaviour of naturally aged Al-Cu-Li alloy [J]. International Journal of Plasticity, 2017, 89: 130-149.
[66] ZHANG Q, ZHANG W Z, LIU Y Y. Evaluation and mathematical modeling of asymmetric tensile and compressive creep in aluminum alloy ZL109 [J]. Materials Science and Engineering A, 2015, 628: 340-349.
[67] BROWN D W, BEYERLEIN I J, SISNEROS T A, CLAUSEN B, TOME C N. Role of twinning and slip during compressive deformation of beryllium as a function of strain rate [J]. International Journal of Plasticity, 2012, 29: 120-135.
李子涵1,周国伟2,李大永1,3,汪华苗1,唐伟琴1,彭颖红1,Hatem S. ZUROB4,吴沛东5
1. 上海交通大学 机械系统与振动国家重点实验室,上海 200240;
2. Department of Materials Science and Engineering, Ohio State University, Columbus, Ohio 43212, USA;
3. 上海交通大学 材料基因组联合研究中心,上海 200240;
4. Department of Materials Science and Engineering, McMaster University, Hamilton, Ontario L8S 4G7, Canada;
5. Department of Mechanical Engineering, McMaster University, Hamilton, Ontario L8S 4G7, Canada
摘 要:建立一种耦合滑移、动态再结晶以及晶界滑移的晶体塑性模型以仿真镁合金的高温变形行为及织构演化。首先,通过实验测量单轴拉伸、压缩后的织构以及显微组织演化,研究AZ31B镁合金在300 °C 的变形机制。结果发现,动态再结晶在应变小于0.2时起到细化晶粒的作用,之后晶界滑移在变形过程中起显著作用。此外,建立晶界滑移模型来评估由晶界滑移产生的应变以及晶粒转动,并与多晶体塑性模型VPSC相耦合。所建立的VPSC-DRX-GBS模型可以很好地计算应力-应变曲线、晶粒尺寸、织构演化以及实验中所发现的拉伸与压缩织构演化显著差异。计算的晶界滑移贡献率在拉伸条件下显著高于压缩条件的,这是由于在拉伸时晶界上更易产生孔洞形核。
关键词:镁合金;晶界滑移;动态再结晶;多晶体塑性;织构
(Edited by Wei-ping CHEN)
Corresponding author: Da-yong LI; Tel: +86-21-34206313; E-mail: dyli@sjtu.edu.cn
DOI: 10.1016/S1003-6326(20)65483-8
1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier B.V. & Science Press
2021 The Nonferrous Metals Society of China. Published by Elsevier B.V. & Science Press

