J. Cent. South Univ. (2018) 25: 1295-1305
DOI: https://doi.org/10.1007/s11771-018-3826-4
Hydration film measurement on mica and coal surfaces using atomic force microscopy and interfacial interactions
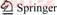
XING Yao-wen(邢耀文)1, GUI Xia-hui(桂夏辉)2, CAO Yi-jun(曹亦俊)2
1. School of Chemical Engineering and Technology, China University of Mining and Technology,Xuzhou 221116, China;
2. Chinese National Engineering Research Center of Coal Preparation and Purification, China University of Mining and Technology, Xuzhou 221116, China
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: The hydration film on particle surface plays an important role in bubble-particle adhesion in mineral flotation process. The thicknesses of the hydration films on natural hydrophobic coal and hydrophilic mica surfaces were measured directly by atomic force microscopy (AFM) based on the bending mode of the nominal constant compliance regime in AFM force curve in the present study. Surface and solid–liquid interfacial energies were calculated to explain the forming mechanism of the hydration film and atomic force microscopy data. The results show that there are significant differences in the structure and thickness of hydration films on coal and mica surfaces. Hydration film formed on mica surface with the thickness of 22.5 nm. In contrast, the bend was not detected in the nominal constant compliance regime. The van der Waals and polar interactions between both mica and coal and water molecules are characterized by an attractive effect, while the polar attractive free energy between water and mica (-87.36 mN/m) is significantly larger than that between water and coal (-32.89 mN/m), which leads to a thicker and firmer hydration layer on the mica surface. The interfacial interaction free energy of the coal/water/bubble is greater than that of mica. The polar attractive force is large enough to overcome the repulsive van der Waals force and the low energy barrier of film rupture, achieving coal particle bubble adhesion with a total interfacial free energy of -56.30 mN/m.
Key words: hydration film; atomic force microscope; surface energy; interfacial interaction
Cite this article as: XING Yao-wen, GUI Xia-hui, CAO Yi-jun. Hydration film measurement on mica and coal surfaces using atomic force microscopy and interfacial interactions [J]. Journal of Central South University, 2018, 25(6): 1295–1305. DOI: https://doi.org/10.1007/s11771-018-3826-4.
1 Introduction
Water molecules near particle surfaces immersed in aqueous liquid may orient toward the surfaces to form hydration film with a higher viscosity and density than bulk water because of the surface free energy and strong attractive interactions between the molecules and the surface [1–3]. When two particles came into contact with each other, a repulsive hydration force was generated because of the overlap of the hydration films. Various studies have proven the existence of multi-layers of adsorbed water molecules on particle surfaces, as confirmed via atomic force microscopy (AFM) and surface force apparatus (SFA) measurements, and the hydration film is of great scientific and technological importance for process engineering of colloidal suspensions such as minerals flotation, agglomeration, separation and adhesion process [4–6].
Froth flotation is an effective separation method for fine coal cleaning and is based on the differences in the surface hydrophobicity of organic compounds and minerals [7–9]. Hydration and thin liquid films play an important role in the sub-process of bubble-particle adhesion [10–12]. With a thin hydration film, hydrophobic coal particles can be separated by attaching themselves to rising air bubbles via attractive hydrophobic interactions and forming froth products, whereas the same cannot be said for hydrophilic gangue particles because of the thicker hydration film and repulsive hydration force [13]. Therefore, the hydration films on different hydrophobic particle surfaces and their effect on flotation process require to be investigated.
Numerous pioneering studies have been conducted to investigate the hydration force and hydration film structure. A typical three-layer model of the water structure at the hydrophilic solid surface has been proposed by DROST-HANSEN [14], as shown in Figure 1. The dipole–dipole interaction on a hydrophilic surface causes an ordering of the water molecules, thereby leading to a notable disordered zone. While NGUYEN et al [10] claimed that the water molecules on a hydrophobic surface had extensive clathrate-like structure with a minimal disordered zone. In recent years, rapid development of advanced analytical methods and quantum chemistry simulations has enabled basic theoretical research on mineral processing to examine materials at nanoscale. Traditional optical microscopy has been displaced by micro-zone and micro-beam technologies, such as electron microscopy and electron probe measurements. The microstructure and physicochemical properties of minerals can be obtained via atomic-scale simulations, which are used to predict and explain experimental phenomena in mineral processing. LI et al [15] used the dynamic procedure of AFM to study the layers of water molecules, ions, and hydrated ions adsorbed on solid surfaces in NaCl solutions. Two types of structured layers were found at the interface of solid surfaces in electrolyte solutions: a thin but firm primary layer and a thick but fragile secondary layer located outside the primary layer. The fragile secondary layer has also been reported by other researchers [16–18]. FENTER et al [19] claimed that synchrotron-based X-ray scattering technique was a powerful method to investigate mineral–water interfacial structures. Recently, molecular dynamics (MD) simulations have been used to explore water–water and water–mineral interactions and to elucidate the interfacial water structure and configuration of water molecules at the surface of minerals [20–22]. In these simulations, the hydrophobic surfaces, such as that of sepiolite or the talc basal plane, were not in close contact with water molecules because of the absence of hydrogen bonding sites. The MD simulation result of the sepiolite–water interfacial structure and the density distribution along the normal direction to the sepiolite crystal surface is shown in Figure 2. The water structure of K2SO4 and MgSO4 or alkali halide salts solutions can also be investigated by FTIR-transmission and FTIR- ATR methods [23, 24]. The “ice-like” and “liquid” water structures can be directly determined as revealed by the change of the O—H band position on the FTIR spectrum.
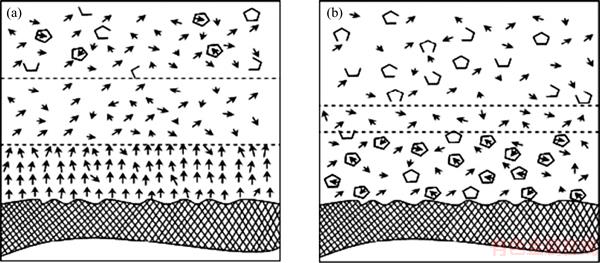
Figure 1 Water structure at hydrophilic (a) and hydrophobic surfaces (b) [10]
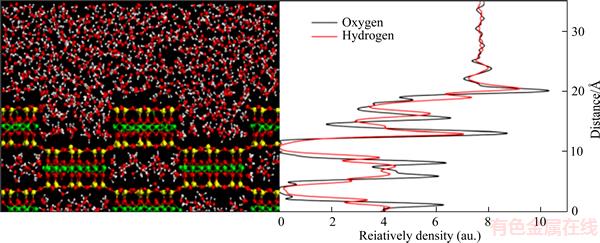
Figure 2 MD simulation result of sepiolite–water interfacial structure and density along sepiolite crystal surface normal (red–oxygen atoms; white–hydrogen atoms; yellow–silicon atoms, and green–magnesium atoms) [22]
The formation of a hydration film is the most accepted explanation for the repulsive hydration force. PASHLEY [25, 26] found that a hydration force exists between hydrophilic mica surfaces in aqueous electrolyte solutions by using SFA. Interfacial forces between silica surfaces were also measured via AFM and the colloid probe technique [27, 28]. The difference between the prediction of the DLVO theory and the AFM measurements revealed the existence of a strong, short-range repulsive interaction and a strong disjoining pressure between the two hydrophilic surfaces.
Although the hydration film structure and hydration force have been the focus of multiple studies, only a few reports have focused on determining the hydration film thickness. Recently, an innovative technique was developed to extract the thickness of a hydration film by detecting changes in the shape of the AFM force–distance curve of a solid surface immersed in aqueous solutions [29, 30]. The film was treated as a new firm material of known yielding stress overlaying the substrate. An ideal AFM force–distance plot of a mica plate in water is shown in Figure 3. At point 2, the tip jumped into contact with the surface of the hydration layer. At this stage, the AFM probe continued its downward approach and the cantilever further deflected by an amount equal to the piezoelectric transducer displacement (point 2 to point 3). When the tip-sample force became equal to the yielding stress of the film, the tip penetrated the hydration film and contacted the sample surface directly (between points 3 and 4). The difference in the cantilever deflection and piezoelectric transducer displacement from point 3 to point 4 was defined as the thickness of hydration film on the tips and solid surface. However, only hydration film on the hydrophilic mica surface was studied in Peng’s report. For fine coal flotation system, it is essential to further investigate the thicknesses of hydration films on different hydrophobic particle surfaces and their effect on flotation process, which can give us a more comprehensive understanding of fine coal flotation.
Figure 3 Ideal AFM force–distance plot of mica plate in water [29]
In the present study, the method based on the bending mode in the AFM force curve nominal constant compliance regime was used to measure the thicknesses of the hydration films on hydrophobic coal and hydrophilic mica surfaces, respectively. Meanwhile, the surface energy and solid–liquid interfacial energy were calculated to explain the AFM results as the surface free energy strongly influences substrate adhesiveness and wettability as well as the thickness of the hydration film [31, 32]. By analyzing the thickness of the hydration film, much information could be obtained to deepen our understanding on the coal flotation process. The outcome of this study will provide guidance for the improvement of fine coal flotation efficiency.
2 Experimental
2.1 Materials
Flat pure coal and mica plates were used as the substrates for hydration film measurement. Lump coal samples with 20.27% ash content were collected from a coal preparation plant in Shandong Province, China. Float-sink test with a 1.35 g/cm3 density heavy liquids was conducted to separate the low ash fractions with 5.75% ash content. The coal surface substrate was prepared by following steps. First, the purified coal was subjected to cutting with a diamond saw. Then rough grinding, fine grinding, lapping finish, and polishing using a metallographic polishing machine (ZMP-2000) were conducted to prepare the coal substrate. Samples of pure mica lump (V-1grade) were purchased from Jinnuo Mineral Processing Factory in Hebei Province, China. The coal and mica plates were then thoroughly rinsed with deionized water, alcohol, and deionized water sequentially. Finally, the samples were dried by blowing pure nitrogen gas over the surface and then used for hydration film measurement.
2.2 Hydration film thickness measurement by AFM
All of the experiments were conducted using a 5500-A-1120 AFM (Agilent, America) in contact mode. Hydrophilic triangular silicon nitride cantilevers were chosen to conduct force measurement. The working principle of AFM has been described in detail elsewhere [33, 34]. Before the force curve experiment, plasma cleaner (Harrick PDC-32G-2, America) was used to remove the potential hydrophobic material absorbed onto the probe. Milli-Q water was injected into the liquid cell holder at a low speed by using a micro syringe to minimize bubble formation on the sample surface. The AFM test was conducted for half an hour after injection. To eliminate the introduction of errors from a hydrodynamic force, the piezo displacement speed was kept below 2 μm/s [35]. The cantilever deflection versus piezoelectric transducer displacement profile was recorded. The film was treated as a new firm material of known yielding stress overlaying the substrate. When the tip jumped into contact with the surface of the hydration layer, the applied force was lower than the yield stress of the film. At this stage, the deflection of AFM level was equal to the piezo displacement. A nominal constant compliance regime was observed. With AFM probe continuing its downward approach and the cantilever further deflected, the tip penetrated the hydration film and contacted the sample surface directly (true hard contact), leading to the bend of the AFM force curve. The thickness of hydration film was calculated by subtraction of the piezoelectric transducer displacement and cantilever deflection during the penetration stage according to PENG’s method (the bend in the nominal constant compliance regime). The schematic diagram of the calculation of the hydration film thickness is shown in Figure 4. All of the measurements were carried out five times at a room temperature of (20±1) °C, and the average values were presented. In the present investigation, the cantilever remained stationary, while the sample was attached to the piezoelectric ceramic platform. This ensured that the sample was as close as possible to the tip. It should be noted that the roughness and porosity on coal surface will significantly affect the AFM measurement result. So, the coal surface was characterized by AFM imaging prior to the film thickness measurements, which allows the selection of suitable locations (with relatively small roughness).
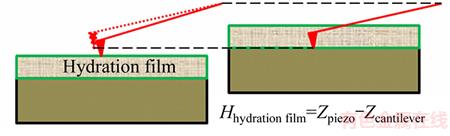
Figure 4 Schematic diagram of calculation of hydration film thickness
2.3 Calculation method of surface free energy and interfacial interaction energy
The hydration film is the result of intermolecular interactions between water molecules and a solid surface, and it is influenced by the surface properties of the particle, especially the substrate’s surface free energy. Therefore, accurately determining the surface energy of the minerals leads to a basic understanding of the mechanism of hydration film formation, which is necessary to better control the conditions required for high efficiency flotation [36].
The total surface free energy γ is composed of two parts: the non-polar part γLW (i.e., Lifshitz–van der Waals) and the polar part γAB (i.e., Lewis acid–base) according to the van Oss–Chaudhury– Good theory [37, 38]. The non-polar dispersive component is mainly attributed to London forces, while the polar component (Lewis acid–base interactions) is mainly associated with hydrogen bonding and the behaviour of the electron donor–acceptor (i.e., γ– and γ+) [39–41]. The surface free energy of the solid γS and the liquid γL can be calculated as [42, 43]:
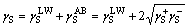(1)
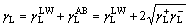(2)
According to the Dupre equation, the solid–liquid interfacial free energy γSL is expressed as [36, 41]:
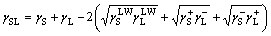(3)
By combining Eqs. (1), (2), and (3), and Young’s equation, Eq. (4) is obtained [44, 45].
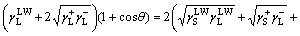
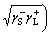(4)
Based on Eq. (4), the solid surface energy and its components can be obtained by measuring the contact angles of three different liquids (two polar liquids are required).
In addition, the interfacial interaction free energy △GSL between a solid and a liquid can be divided into two parts: the first component results from the non-covalent long-range Lifshitz–van der Waals free energy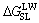 
and the second component is from the Lewis acid–base free energy [46, 47].
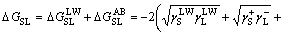
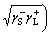(5)
By using a liquid (deionized water) as the intermediate phase, the interfacial free energy of a solid and a gas bubble via liquid phase △GSLG can be calculated by Eq. (6) [48].
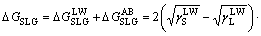
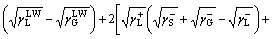
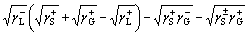(6)
3 Results and discussion
3.1 Selection of AFM cantilever
The precise selection of AFM cantilever (i.e. spring constant k of cantilever) is the premise to obtain the hydration film thickness information. This parameter defines how flexible the lever is, which transpires to be an important characteristic for force studies. When a too stiff cantilever was chosen, it may be difficult to identify the change in the shape of the AFM force–distance curve because of the loss of sensitivity. The yield stress is too low to produce obvious cantilever deformation. Conversely, when a too soft cantilever was chosen, the excessive deformation in response to the applied force may lead to the fact that the photoelectric detector cannot receive the reflected laser light signal. Therefore, the spring constant of the cantilever must be chosen based on the expected magnitudes of yield force of the hydration film that are to be observed. In the present study, three kinds of AFM cantilevers, with 0.5044, 0.1381, and 0.039 N/m spring constants after calibration by using AFM software, were chosen to measure the thickness of smooth mica, respectively. The AFM force curves are shown in Figures 5–7. When the spring constants were 0.5044 and 0.1381 N/m, the typical constant compliance regime were observed which indicate that AFM tip directly contacted with mica surface (hard contact). The applied force was much higher than the yield force, missing film information at close approach. When the spring constant decreased to 0.039 N/m, the bending mode was observed in the nominal constant compliance regime. This bend of the AFM force curve can be attributed to that the tip penetrated of the hydration film and contacted the sample surface directly. In the following experiment, the cantilever with 0.039 N/m spring constant was used to measure the thickness of hydration film.
3.2 Hydration film thickness on mica and coal surfaces
Extracting the approaching curve from Figure 7, the calculation for the hydration film thickness on the smooth mica surface is shown in Figure 8. The inflection points in the nominal constant compliance regime were determined by drawing the tangent line. Therefore, the thickness of the hydration film on the mica surface can be expressed as: H=(2165-2065)-(272.5-194)=22.5 nm.
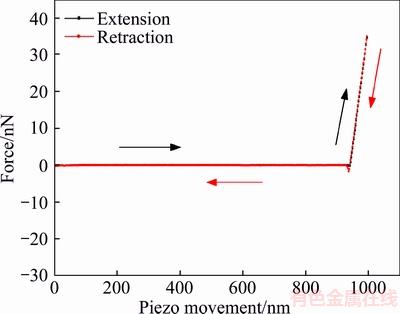
Figure 5 Force curves for interaction between tip and hydrophilic mica surface in deionized water (k=0.5044 N/m)
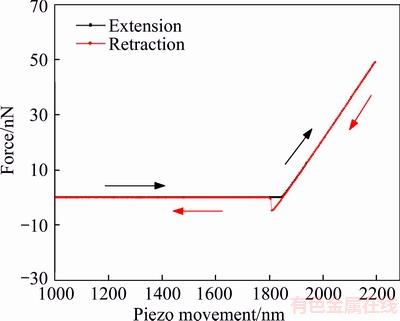
Figure 6 Force curves for interaction between tip and hydrophilic mica surface in deionized water (k=0.1381 N/m)
Figure 7 Force curves for interaction between tip and hydrophilic mica surface in deionized water (k=0. 0.0390 N/m)
Before the measurement of coal surface hydration film, the topographical images of the coal surfaces were firstly obtained using the contact mode on the AFM. The force curves experiments were conducted at least six times at same locations of the coal substrate where the surface roughness was relatively small. The cantilever deflection– piezo movement curve for coal is shown in Figure 9. Different to mica’s case, the bend was not detected in the nominal constant compliance regime. To verify this point, the instantaneous slope of the cantilever deflection–piezo movement curve for coal in Figure 9 was calculated. The result is shown in Figure 10. There was no obvious change in the curve slope during the contact region, which was nearly kept constant at –0.6. It means that the tip contacted with coal surface directly and hydration film may not form on hydrophobic coal surface or the hydrogen film is too thin to be detected out by using the present method.
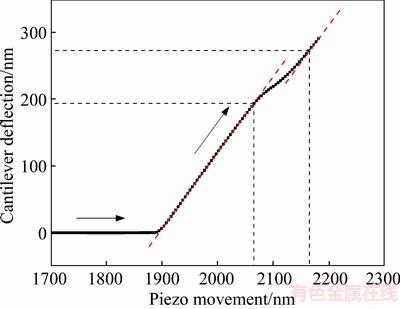
Figure 8 Calculation of hydration film thickness on hydrophilic mica surface
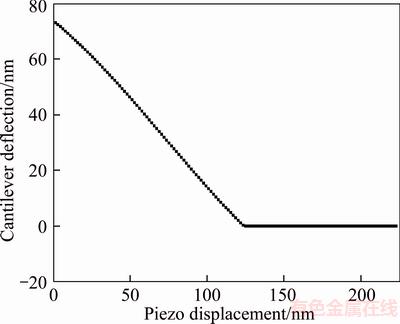
Figure 9 Cantilever deflection–piezo movement curve for coal in deionized water
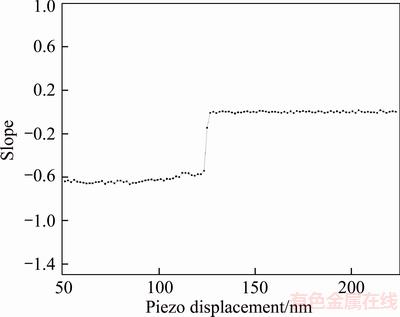
Figure 10 Instantaneous slope of cantilever deflection– piezo movement curve for coal in Figure 9 in deionized water
These results illustrate that significant differences exist in the structure and thickness of the hydration films on coal and mica surfaces. From the perspective of flotation kinetics, the collection efficiency is the consequence of three sub-processes, namely collision, attachment and detachment in the overall collection process. It indicates that an ultimate success of the flotation process depends on the capture of particles of interest by bubbles in the pulp phase and the successful transfer of the aggregate to the froth phase [49]. It is well established that probability of bubble–particle attachment Pa can be expressed as [50]:
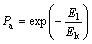(7)
where E1 is energy barrier for bubble-particle attachment; Ek is the kinetic energy of a particle approaching a bubble.
During the bubble–particle mineralization process, a thinning rupture of the hydration film on the hydrophilic surface may not occur because of the existence of the firm layer and a high energy barrier E1, denying bubble–particle adhesion. However, hydration film did not form on hydrophobic coal surface, thereby allowing bubble– particle adhesion to occur (only a small kinetic energy Ek is needed). Thus, coal particles are separated by allowing them to attach to rising air bubbles, which results in the formation of a particle-rich froth on the suspension surface.
3.3 Surface free energy and interfacial interaction energy
The calculation of surface free energy and interfacial interaction energy can qualitatively explain the formation mechanism of hydration film and AFM results. A DSA25 (Kruss, Germany) was used to measure the contact angle between the test liquids (α-bromonaphthalene, formamide, and deionized water) and the mica or coal surface. The physical parameters of the test liquids (analytical grade) are listed in Table 1. All of the experiments were carried out five times at room temperature ((20±1) °C), and the average values are presented.
Table 1 Physical parameters of test liquids
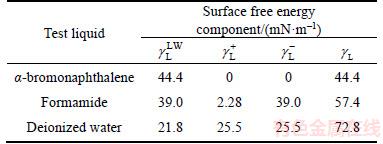
The contact angles of the test liquids and the surface free energy components associated with the coal and mica samples are shown in Table 2. It can be clearly observed that hydrophilic mica has a relatively high surface energy compared with that of coal. The surface energies of the dispersive components for the two samples were quite close. However, a significant difference was observed in the specific (acid–base) components, especially for the base component. For example, the surface energy of the electron acceptor and donor components of the coal (mica) surface are 0.05 (1.01) and 9.26 (58.46) mN/m, respectively. According to van-Oss and Giese’s classification method,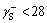 
mN/m is characterized as a hydrophobic surface and 
mN/m is deemed to be a hydrophilic surface [51]. This indicates that mica presents highly polar and hydrophilic features.
Table 2 Contact angles of test liquids and surface free energy components of coal and mica samples
The values for the interfacial interaction free energy △GSL are shown in Table 3. The Lifshitz–van der Waals and the Lewis acid–base free energies between mica/coal and water are all less than 0. This result indicates that the van der Waals force and polar interaction force between the solid and water are characterized by an attractive effect. However, the polar attractive free energy between mica and water (–87.36 mN/m) is significantly larger than that of coal (–32.89 mN/m). This explains why a thicker and firmer layer forms on the mica surface compared with that of coal. It should be noted that hydration film also forms on coal surface because of the attractive force. This illustrates that AFM force curve bending method was limited by system sensitivity and hydrogen film on coal surface is too thin to be detected out by using the present method. The interfacial interaction free energies of the solid/water/bubble △GSLG are also shown in Table 3. The Lifshitz–van der Waals interaction energies are all greater than 0 for mica and coal, which indicates that the van der Waals force between a particle and a bubble in aqueous solution is repulsive. However, the Lewis acid–base interaction energies are less than 0, which indicates that the polar interaction force is attractive. The interfacial interaction free energy of the coal/water/bubble (–56.30 mN/m) is greater than that of mica (–1.49 mN/m). The polar attractive force is large enough to overcome the repulsive van der Waals force and the low energy barrier that is required for film rupture. Thus, bubble–particle adhesion occurs with a total interfacial interaction free energy of -56.30 mN/m. The polar attractive energy for mica is only -14.64 mN/m and failed to overcome the high energy barrier required for film rupture. This therefore leads to a re-bonding of mica particles and a separation from the bubble surface. This mechanism is the basic reason for the separation of coal and hydrophilic particles. The principle of flotation separation, as it applies to mica and coal, is shown in Figure 11.
Table 3 Interfacial interaction free energy △GSL and △GSLG (mN·m–1)
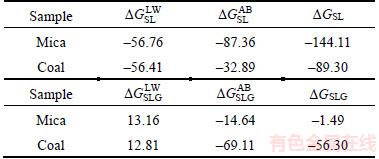
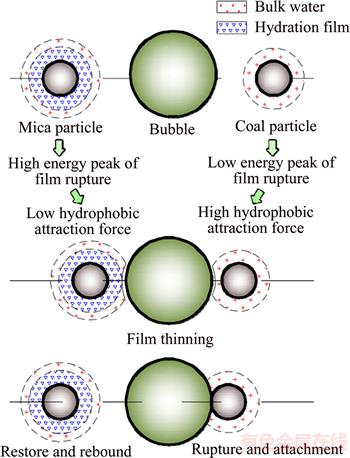
Figure 11 Separation principle of mica and coal in flotation separation
4 Conclusions
The method based on the bending mode of the nominal constant compliance regime in the AFM force curve can be used to measure the thicknesses of the hydration films on hydrophobic coal and hydrophilic mica surfaces, respectively. Based on AFM studies, there are significant differences in the structure and thickness of hydration films on coal and mica surfaces. Hydration film formed on mica surface with the thickness of 22.5 nm. In contrast, the bend was not detected in the nominal constant compliance regime. Hydration film may not form on hydrophobic coal surface or the hydrogen film is too thin to be detected out by using the present method.
Hydrophilic mica has a higher surface energy than coal. The van der Waals and polar interaction forces between both coal and mica and water are characterized by an attractive effect, which leads to the formation of hydration film on both mica and coal surface. However, the polar attractive free energy between mica and water (–87.36 mN/m) is significantly larger than that of coal (–32.89 mN/m). This is the reason why a thicker and firmer layer is formed on the mica surface. AFM force curve bending method was limited by system sensitivity and hydrogen film on coal surface is too thin to be detected out by using the present method. Moreover, the interfacial interaction free energy of the coal/water/bubble is greater than that of the mica/water/bubble. The polar attractive force is large enough to overcome the repulsive van der Waals force and the low energy barrier of film rupture. Thus, bubble–particle adhesion occurs with a total interfacial interaction free energy of -56.30 mN/m.
However, this study only focused on films forming on flat solid surfaces, which is quite different from a true mineral flotation system. Therefore, further work is also required to study the hydration film and the surface energy associated with powder particles.
References
[1] QIU Guan-zhou, HU Yue-hua, WANG Dian-zuo. Interactions between particles and flotation of fine particles [M]. Changsha: Press of Central South University of Technology, 1993: 81–91. (in Chinese)
[2] SONG Shao-xian, ZHANG Yi-min, TOMLINSON F. Viscosity method for the determination of the thickness of solvation layers near particles dispersed in a liquid [J]. Surface Review and Letters, 2005, 12(3): 457–462.
[3] PENG Chen-liang, MIN Fan-fei, ZHAO Qing, LI Hong-liang. A review: Research status and progress on hydration layers near fine mineral particles [J]. Acta Minalogica Sinica, 2012, 32(4): 515–522. (in Chinese)
[4] ISRAELACHVILI J N, MCGUIGGAN P M. Forces between surfaces in liquids [J]. Science, 1988, 241: 795–800.
[5] HIENEBZ P C, RAJAGOPALAN R. Principles of colloid and surface chemistry [M]. New York: Marcel Dekker, 1997: 145–181.
[6] MIN Fan-fei, PENG Chen-liang, LIU Ling-yun. Investigation on hydration layers of fine clay mineral particles in different electrolyte aqueous solutions [J]. Powder Technology, 2015, 283: 368 –372.
[7] JENA M S, BISWAL S K, DAS S P, REDDY P S. Comparative study of the performance of conventional and column flotation when treating coking coal fines [J]. Fuel Processing Technology, 2008, 89: 1409–1415.
[8] XING Yao-wen, GUI Xia-hui, LIU Jiong-tian, CAO Yi-jun, LU Yu. Effects of energy input on the laboratory column flotation of fine coal [J]. Separation Science and Technology, 2015, 50(16): 2559–2567.
[9] GONG Mao-ming, LI Chun-shan, LI Zeng-xi. Numerical analysis of flow in a highly efficient flotation column [J]. Asia–Pacific Journal of Chemical Engineering, 2015, 10(1): 84–95.
[10] NGUYEN A V, SCHULZE H J. Colloidal science of flotation [M]. New York: Marcel Dekker, 2004.
[11] PAN LEI, JUNG S, YOON R H. Effect of hydrophobicity on the stability of the wetting films of water formed on gold surfaces [J]. Journal of Colloid and Interface Science, 2011, 361: 321–330.
[12] PAN L, JUNG S, YOON R H. A fundamental study on the role of collector in the kinetics of bubble-particle interaction [J]. International Journal of Mineral Processing, 2012, 106–109(2): 37–41.
[13] NGUYEN A V. Froth flotation [M]// Reference Module in Chemistry, Molecular Sciences and Chemical Engineering. 2013: 1–26.
[14] DROST-HANSEN W. Effects of vicinal water on colloidal stability and sedimentation processes [J]. Journal of Colloid and Interface Science, 1977, 58(2): 251–262.
[15] LI Ying, KANDA Y, SHINTO H, HIGASHITANI K. Fragile structured layers on surfaces detected by dynamic atomic force microscopy in aqueous electrolyte solutions [J]. Advanced Powder Technology, 2005, 16(3): 213–229.
[16] LYKLEMA J, ROVILLARD S, CONINCK J D. Electrokinetics: The properties of the stagnant layer unraveled [J]. Langmuir, 1998, 14: 5659–5663.
[17] VAKARELSKI I U, HIGASHIYANI K. Dynamic features of short-range interaction force and adhesion in solutions [J]. Journal of Colloid and Interface Science, 2001, 242: 110–120.
[18] KIM H I, KUSHMERICK J G, HOUSTON J E, BUNKER B C. Viscous ‘interphase’ water adjacent to oligo (ethylene glycol)-terminated monolayers [J]. Langmuir, 2003, 19: 9271–9275.
[19] FENTER P, STURCHIO N C. Mineral–water interfacial structures revealed by synchrotron X-ray scattering [J]. Progress in Surface Science, 2004, 77: 171–258.
[20] WANG Jian-wei, KALINICHEV A G, KIRKPATRICK R J. Effects of substrate structure and composition on the structure, dynamics, and energetics of water at mineral surfaces: A molecular dynamics modeling study [J]. Geochimica et Cosmochimica Acta, 2006, 70: 562–582.
[21] DU Hao, MILLER J D. A molecular dynamics simulation study of water structure and adsorption states at talc surfaces [J]. International Journal of Mineral Processing, 2007, 84: 172–184.
[22] BENLI B, DU Hao, CELIK M S. The anisotropic characteristics of natural fibrous sepiolite as revealed by contact angle, surface free energy, AFM and molecular dynamics simulation [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2012, 408: 22–31.
[23] CHENG Fang-qin, CAO Qin-bo, GUAN Yun-shan, WANG Xu-ming, MILLER J D. FTIR analysis of water structure and its influence on the flotation of arcanite (K2SO4) and epsomite (MgSO4·7H2O) [J]. International Journal of Mineral Processing, 2013, 122: 36–42.
[24] NICKOLOV Z S, MILLER J D. Water structure in aqueous solutions of alkali halide salts: FTIR spectroscopy of the OD stretching band [J]. Journal of Colloid and Interface Science, 2005, 287: 572–580.
[25] PASHLEY R M. Hydration forces between mica surfaces in aqueous electrolyte solutions [J]. Journal of Colloid and Interface Science, 1981, 80: 153–162.
[26] PASHLEY R M. Hydration forces between mica surfaces in electrolyte solution [J]. Advances in Colloid and Interface Science, 1982, 16: 57–62.
[27] YOON R H, VIVEK S. Effects of short-chain alcohols and pyridine on the hydration forces between silica surfaces [J]. Journal of Colloid and Interface Science, 1998, 204(1): 179–186.
[28] VALLE-DELGADO J J, MOLINA-BOLIVAR J A, GALISTEO-GONZALEZ F, GALVEZ-RUIZ M J, FEILER A, RUTLAND M W. Hydration forces between silica surfaces: Experimental data and predictions from different theories [J]. The Journal of Chemical Physics, 2005, 123(3): 21–33.
[29] PENG Cheng-sheng, SONG Shao-xian. Determination of thickness of hydration layers on mica in aqueous solutions by using AFM [J]. Surface Review and Letters, 2004, 11(6): 485–489.
[30] PENG Cheng-sheng, SONG Shao-xian, GU Qing-bao. Determination of hydration film thickness using atomic force microscopy [J]. Chinese Science Bulletin, 2005, 50(4): 299–304.
[31] WANG Hui, CHEN Li, FU Jian-gang, HAO Ye. Interface thermodynamics of molybdenite floatation system [J]. Journal of Central South University, 2007, 38(5): 893–899. (in Chinese)
[32] MOHAMMADI-JAM S, BURNETT D J, WATERS K E. Surface energy of minerals – Applications to flotation [J]. Minerals Engineering, 2014, 66–68: 112–118.
[33] NGUYEN A V, NALASKOWSKI J, MILLER J D. A study of bubble–particle interaction using atomic force microscopy [J]. Minerals Engineering, 2003, 16: 1173–1181.
[34] ASSEMI S, NGUYEN A V, MILLER J D. Direct measurement of particle–bubble interaction forces using atomic force microscopy [J]. International Journal of Mineral Processing, 2008, 89: 65–70.
[35] REN Si-li, MASLIYAH J, XU Zheng-he. Studying bitumen–bubble interactions using atomic force microscopy [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2014, 444: 165–172.
[36] RAICHUR A M, WANG X H, PAREKH B K. Estimation ofsurfacefreeenergyof pyrites by contact angle measurements [J]. Minerals Engineering,2001, 14(1): 65–75.
[37] VAN-OSS C J, CHAUDHURY M K, GOOD R J. Mechanism of partition in aqueous media [J]. Separation Science and Technology, 1987, 22(6): 1515-1526.
[38] VAN-OSS C J, GOOD R J, CHAUDHURY M K. Estimation of the polar surface tension parameters of glycerol and formamide, for use in contact angle measurements on polar solids [J]. Journal of Dispersion Science and Technology, 1990, 11(1): 75-81.
[39] VAN-OSS C J, GOOD R J, CHAUDHURY M K. The role of van der Waals forces and hydrogen bonds in “hydrophobic interactions” between biopolymers and low energy surfaces [J]. Journal of Colloid and Interface Science, 1986, 111: 378–390.
[40] VOELKEL A, STRZEMIECKA B, ADAMSKA K, MILCZEWSKA K. Inverse gas chromatography as a source of physiochemical data [J]. Journal of Chromatography A, 2009, 1216: 1551–1566.
[41] ZOU Wen-jie, CAO Yi-jun, LIU Jiong-tian, LI Wei-na, LIU Chang. Wetting process and surface free energy components of two fine liberated middling bituminous coals and their flotation behaviors [J]. Powder Technology, 2013, 246: 669–676.
[42] SCHULTZ J, LAVIELLE L, MARTIN C. The role of the interface in carbon fibre-epoxy composites [J]. The Journal of Adhesion, 1987, 23: 45–60.
[43] ALI S S M, HENG J Y Y, NIKOLAEV A A, WATERS K E. Introducing inverse gas chromatography as a method of determining the surface heterogeneity of minerals for flotation[J]. Powder Technology, 2013, 249: 373–377.
[44] FAN Gui-xia, CAO Yi-jun, ZHANG Feng-wei. Investigation on the surface wettability and surface free energy of micro fine ilmenite and titanaugite [J]. Journal of China University of Mining & Technology, 2014, 43(6): 1051–1057. (in Chinese)
[45] HOYSE L. Surface free energy and floatability of low-rank coal [J]. Fuel, 1996, 75(6): 737–742.
[46] ESPINOSA-JIMENEZ M, ONTIVEROS-ORTEGA A, GIMENEZ-MARTIN E. Surface energetics of the adsorption process of a cationic dye on leacril fabrics [J]. Journal of Colloid and Interface Science, 1997, 194(2): 419-426.
[47] ESPINOSA-JIMENEZ M, GIMENEZ-MARTIN E, ONTIVEROS-ORTEGA A. Effect of tannic acid on the ζ potential, sorption and surface free energy in the process of dyeing of leacril with a cationic dye [J]. Journal of Colloid and Interface Science, 1998, 207(1): 170-179.
[48] WU Wen-ju, GIESE R F, VAN-OSS C J. Stability versus flocculation of particle suspensions in water: Correlation with the extended DLVO approach for aqueous systems, compared with classical DLVO theory [J]. Colloids and Surfaces B: Biointerfaces, 1999, 14(1–4): 47-55.
[49] AHMED N, JAMESON G J. Flotation kinetics [J]. Mineral Processing and Extractive Metallurgy Review, 1989, 5: 77-99.
[50] YOON R H, MAO Lai-qun. Application of extended DLVO theory, IV–derivation of flotation rate equation from first principles [J]. Journal of Colloid and Interface Science, 1996, 181: 613–626.
[51] VAN-OSS C J, GIESE R F. The hydrophilicity and hydrophobicity of clay minerals [J]. Clays and Clay Minerals, 1995, 43: 474–477.
(Edited by YANG Hua)
中文导读
原子力显微镜的云母及煤表面的水化膜测试和界面相互作用
摘要：颗粒表面水化膜在浮选颗粒气泡粘附过程中扮演着重要作用。借助原子力显微镜力曲线中名义恒定区的弯曲现象完成对天然亲水性云母和疏水性煤片表面水化膜厚度的测试。同时，对表面能及固液界面自由能进行计算揭示了水化膜的形成机制。结果发现：云母和煤表面的水化膜厚度和结构存在明显的差异，云母表面的水化膜厚度为22.5 nm，而在煤表面并未检测到水化膜的存在。云母及煤与水分子间的范德华和极性作用均为吸引，但云母与水分子间的极性作用能（-87.36 mN/m）远大于煤水间的(-32.89 mN/m)，因此，直接导致了更厚而坚固的水化膜。进一步发现煤–水气泡体系的界面作用自由能（-56.30 mN/m）显著大于云母体系的，极性吸引力足以克服排斥性范德华力和颗粒气泡粘附能垒。
关键词：水化膜；原子力显微镜；表面能；界面作用
Foundation item: Project(2014BAB01B03) supported by the National Key Technology R&D Program During the 12th Five-Yean Plan of China; Project(51774286) supported by the National Natural Science Foundation of China; Project(BK20150192) supported by the Natural Science Foundation of Jiangsu Province, China
Received date: 2016-05-24; Accepted date: 2016-07-07
Corresponding author: GUI Xia-hui, PhD, Professor; Tel: +86-13775989229; E-mail: guixiahui1985@163.com; ORCID: 0000-0001- 9270-7756
