特低渗透断块油藏不规则三角形井网有效动用系数计算及应用
齐亚东1, 3，雷群2，杨正明1, 3，何英1, 3，骆瑛4，杨鹏4
(1. 中国科学院 渗流流体力学研究所，河北 廊坊，065007；
2. 中国石油勘探开发研究院，北京，100083；
3. 中国石油勘探开发研究院廊坊分院，河北 廊坊，065007；
4. 江苏油田地质科学研究院，江苏 扬州，225009)
摘要：针对断块油藏的布井方式，考虑特低渗透储层流体非线性渗流特征，从非线性渗流基本公式出发，应用流管积分法推导不规则三角形井网有效动用系数计算公式，并分析注采压力差、井网几何形状及非线性渗流曲线等因素对有效动用系数的影响，进而将研究成果应用于江苏油田花17断块井网评价中并提出井网调整方案。研究结果表明：均质各向同性特低渗透断块油藏适合部署等腰或近等腰三角形井网；当井网形状偏离等腰三角形程度较高时，存在引起有效动用系数突变的注采压力差和井距；渗透率较大的储层，宜通过放大注采压力差来提高有效动用系数，而渗透率较小的储层，缩小井、排距为更有效的手段。
关键词：特低渗透率；断块油藏；不规则三角形井网；非线性渗流；流管积分法；有效动用系数
中图分类号：TE347 文献标志码：A 文章编号：1672-7207(2012)03-1065-07
Calculation and application of effective development coefficient for irregular triangular patterns in extra-low permeability fault block oil reservoirs
QI Ya-dong1, 3, LEI Qun2, YANG Zheng-ming1, 3, HE Ying1, 3, LUO Ying4, YANG Peng4
(1. Institute of Porous Flow and Fluid Mechanics, CAS, Langfang 065007, China;
2. PetroChina Research Institute of Petroleum Exploration and Development, Beijing 100083, China;
3. PetroChina Research Institute of Petroleum Exploration and Development (Langfang), Langfang 065007, China;
4. Geological Science Research Institute, Jiangsu Petroleum Exploration Bureau, Yangzhou 225009, China)
Abstract: Based on the popular pattern shapes in fault block oilfields and the nonlinear characteristics of the fluids flow in extra-low permeability reservoirs, the expression of effective development coefficient was derived through the streamtube-integration method, and then the effects of pressure difference, well patterns geometry and the shapes of nonlinear flow curves on EDC were analyzed. The new theory was applied to evaluate the well patterns in Hua 17 Block in Jiangsu Oilfield, and a proposal for patterns adjustment was put forward. The results show that in homogeneous isotropic extra-low permeability fault-block reservoirs, the optimal well patterns are those in the shapes of isosceles or quasi-isosceles triangles; for a certain non-isosceles triangle pattern, there is a critical pressure difference and a critical well spacing value bringing the EDC on abrupt changes; and increasing pressure difference is an effective measure to improve the development effect for relatively higher permeability reservoirs while reducing well spacing or row spacing is effective for the relatively lower ones.
Key words: extra-low permeability; fault block oil reservoirs; irregular triangular patterns; non-linear flow; streamtube- integration; effective development coefficient
特低渗透油藏具有孔隙结构复杂，固液作用强等特征，其流体在低速流动过程中不再遵循经典的达西定律，而是呈现非线性渗流特征[1-8]，即渗流曲线存在弯曲段[9]。理论研究及矿场实践表明：以往基于达西渗流理论的油藏工程方法在特低渗透油田开发中已不再适用，亟待改进以满足特低渗透油藏研究的需要，因而，近年来针对此方向的研究取得了较大的进展。计秉玉等[10-11]应用低速非达西渗流基本公式推导了五点法等面积井网以及油水井压裂情况下矩形井网的产量计算公式，为低渗透储层开发提供了理论指导，但该方法建立在拟线性渗流[9]基础之上，对于特低渗透储层而言，拟线性渗流只发生在井筒附近小区域内，而在地层内部相当大的区域内是非线性渗流[9]，若应用文献[10-11]中方法指导特低渗透油田开发会大大低估流体的流动范围；何英[12]研究了适用于特低渗透油藏井网部署的油藏工程方法，该研究主要围绕适用于整装油田的面积井网展开，但对于小断块油田而言，大量发育的断层致使其开发单元小而多，各单元的流体性质、产能和动态等存在显著差异[13]，不适合部署面积井网，因而何英[12]的研究成果在指导小断块油田开发上存在诸多问题。江苏油田的实践证明：不规则三角形井网是一种灵活、实用且有效的井网形式，适合于特低渗透断块油藏开发，但调研结果显示，截至目前尚未见有关特低渗透油藏不规则三角形井网部署的油藏工程方法研究。因而，本文作者从非线性渗流基本公式出发，应用流管积分方法，推导了不规则三角形井网的有效动用系数计算公式，并深入分析了注采压力差、井网几何形状(油井井距、“排距”等)及非线性渗流曲线等多种因素对有效动用系数的影响，最终应用该项研究成果对江苏油田花17断块的井网进行了评价并提出了调整建议。
1 不规则三角形井网有效动用系数计算公式推导
1.1 有效动用系数概念
特低渗透油藏中的流体在低速流动过程中，渗流曲线明显表现出非线性特征，其显著特点之一就是存在非线性渗流段[9]，因此，导致油田生产时，在一定的注采压力差作用下，不是整个井网单元都能动用，将渗流达到稳定时压力梯度能够动用的面积与整个井网单元面积之比定义为有效动用系数，图1所示为有效动用系数示意图(图1中阴影区域代表动用的面积)。它是在中高渗透油藏井网的波及系数基础上，考虑了特低渗透油藏非线性特点而提出的概念，用以衡量储层动用程度从而快速预测和评价井网应用效果。
此概念已经在大庆、吉林和华北等油田的井网评价中得到了应用，并初步得到：当有效动用系数大于等于0.8时，井网能够确保形成有效的驱动压力体系。
图1 有效动用系数示意图
Fig.1 Sketch of effective development coefficient
1.2 不规则三角形井网有效动用系数计算公式推导
假设条件：(1) 多孔介质及流体不可压缩；(2) 稳态渗流；(3) 渗流过程等温；(4) 储层均质各向同性。
非线性渗流运动方程[14]为：
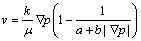(1)
由式(1)可知，任一流管截面上的流量表达式为：
(2)
式中：k为储层渗透率，μm2；μ为地层流体黏度，mPa·s；
为压力梯度，MPa/m；
为流线长度为
处的流管截面积，m2；a为渗流参数，无因次；b为渗流参数，1/MPa。
取一不规则三角形井网，如图2(a)所示。图2(a)中：c和e分别为注水井到两口油井的距离；d为两油井距离。经过大量可靠统计得知，不规则三角形井网可以划分为ABD和ACD 2个流动单元，并且有：
, 
(3)
取流动单元ABD进行研究，假设油水井之间的流场由一系列流管组成，任取一流管微元并进行简化，如图2(b)所示。油水井半径均为rw；油水井距为c；流管中线X1由X11和X12组成；ξ11和ξ12分别为X11和X12上的点到油井和水井的距离；流线在A和B井处与AB所成角度分别为
和
，各自的角增量分别为
和
。
(a) 流动单元划分示意图；(b) 流动单元简化示意图
图2 不规则三角形井网流动单元划分及简化示意图
Fig.2 Division and simplification of flow units in irregular triangle well pattern
流管中线表达式为：
, 
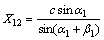(4)
流管截面积表达式：
, 
(5)
(6)
应用流管积分法，可以得到ABD流动单元内产量和有效动用系数计算公式：
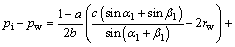
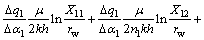
(7)
其中：pi为注水井底压力；pw为生产井底压力；
，
和
如图2(b)所示。
通过数值方法求解式(7)，可获得流量恰好为0的流管微元在A和B井处与AB所成角度
和
。
ABD流动单元的有效动用面积为：
(8)
同理，ACD流动单元内产量和有效动用系数计算公式为：
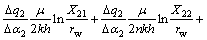
(9)
其中：
；
；
。
ACD流动单元的有效动用面积为：
(10)
其中：
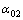和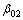
分别为ACD流动单元内流量恰好为0的流管微元在A和C井处与AC所成的角度。
整个井网单元的有效动用系数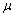
为：
(11)
其中：SABC为整个井网单元的面积。
2 有效动用系数影响因素分析
以某典型特低渗透油藏为例，分析注采压力差、井网几何形状和非线性渗流曲线对有效动用系数的影响。油藏参数为：有效厚度10 m，有效渗透率2×10-3 μm2，地层原油黏度5 mPa·s；渗流系数a=0.28，渗流系数b=19 MPa-1。
井网几何形状表征参数包括：油井井距、注水井到“油井连线”的距离(称为排距)、BE/BC。这3个参数决定了三角形井网的几何形状，如图3所示。
均质各向同性储层情况下，BE/BC取0~0.5的分析结果与取值1~0.5的分析结果完全相同，下文表述基于BE/BC为0~0.5的条件。
图3 不规则三角形井网示意图
Fig.3 Diagram of irregular triangle well pattern
2.1 注采压力差对有效动用系数的影响
在油井井距400 m，排距200 m的情况下，研究了BE/BC取不同比值时注采压力差对有效动用系数的影响，如图4所示。从图4可以看出：在相同的BE/BC条件下，有效动用系数随注采压力差的增大而增大；对于等腰三角形井网(即BE/BC=0.5时)，增大注采压力差后，有效动用系数会有较为显著的提高；对于非等腰三角形井网(即BE/BC≠0.5时)，随注采压力差的增大，有效动用系数存在突变现象，而且井网形状偏离等腰三角形程度越高(即BE/BC越小)，突变现象越明显，突变之前，有效动用系数随注采压力差的增大而增大的趋势较缓，突变之后，有效动用系数随注采压力差的增大而增大的趋势明显增强，出现这一现象的原因是：对于非等腰三角形井网，在一定的注采压力差下，大小不等的2个流动区域不能同时动用。
图4 注采压力差对有效动用系数的影响
Fig.4 Influences of pressure differences on effective development coefficient
因此，当采用非等腰三角形井网开发时，存在一个引起有效动用系数突变的注采压力差值，只有当施工压差大于这个值时，有效动用系数才会随注采压力差的增大而显著提高。为避免这种突变现象，在井网设计时BE/BC取0.4~0.6为宜。
2.2 井网几何形状对有效动用系数的影响
从油井井距、排距和BE/BC 3个方面研究井网几何形状对有效动用系数的影响。
在注采压力差15 MPa，排距250 m的情况下，研究了BE/BC取不同比值时油井井距对有效动用系数的影响，如图5(a)所示。从图5(a)可以看出：在相同的BE/BC条件下，有效动用系数随着油井井距的增大而减小；对于等腰三角形井网(即BE/BC=0.5时)，缩小井距后，有效动用系数会有较为显著的提高；而对于非等腰三角形井网(即BE/BC≠0.5时)，随油井井距的减小，有效动用系数存在突变现象，而且井网形状偏离等腰三角形的程度越高(即BE/BC越小)，突变现象越明显，未达到突变点时，有效动用系数随油井井距的减小而增大的趋势较缓，达到突变点之后，有效动用系数随油井井距的减小而增大的趋势明显加剧，此现象也缘于在一定注采压力差下非等腰三角形井网中2个流动单元不能同时动用。
在注采压力差为15 MPa，油井井距为400 m的情况下，研究了BE/BC取不同值时排距对有效动用系数的影响，如图5(b)所示。从图5(b)可以看出：在相同的BE/BC条件下，有效动用系数随排距的增大而减小；对于等腰三角形井网(即BE/BC=0.5时)，缩小排距时，有效动用系数会有显著提高；而对于非等腰三角形井网(即BE/BC≠0.5时)，井网形状偏离等腰三角形程度越大，有效动用系数随排距的减小而增大的趋势越不明显。
在注采压力差为15 MPa，排距为250 m的情况下，研究了不同油井井距时，BE/BC对有效动用系数的影响，如图5(c)所示。由图5(c)可知：随着井网形状不断接近于等腰三角形，有效动用系数不断增 大，当井网形状为等腰三角形时，有效动用系数达到最大值。
综合以上分析得到：对于均质各向同性储层而言，以部署等腰或近等腰三角形井网为宜，且宜选用小排距；若部署非等腰三角形井网，需注意：存在一个引起有效动用系数突变的油井井距，井网方案所设计的油井井距只有小于此值时，后期调整井距才会有较为显著的效果。
图5 井网几何形状对有效动用系数的影响
Fig.5 Effects of pattern geometry on effective development coefficient
2.3 非线性渗流曲线对有效动用系数的影响
非线性渗流曲线表现出一系列特征[9]，如存在真实启动压力梯度、拟启动压力梯度、非线性曲线段、拟线性段等，现选取真实启动压力梯度为代表，研究非线性渗流曲线对有效动用系数的影响。
在油井井距为250 m，排距为200 m，BE/BC为0.5的情况下，研究了压力差变化时不同真实启动压力梯度对有效动用系数的影响，如图6(a)所示。从图6(a)可以看出：真实启动压力梯度较小时，有效动用系数与注采压力差的关系曲线比较陡峭，即有效动用系数对注采压力差的变化比较敏感，因而对于真实启动压力梯度比较小(渗透率相对较大)的储层而言，通过放大注采压力差的方式来提高有效动用系数较为容易；随着真实启动压力梯度的增大，有效动用系数对注采压力差变化的敏感程度降低，因此，对于真实启动压力梯度较大(渗透率相对较小)的储层而言，通过放大注采压力差的方式来提高有效动用系数较为困难。
图6 真实启动压力梯度对有效动用系数的影响
Fig.6 Effects of pressure gradients on effective development coefficient
在注采压力差为10 MPa，排距与油井井距比为0.8，BE/BC为0.5的情况下，研究了油井井距改变时不同真实启动压力梯度对有效动用系数的影响，如图6(b)所示。从图6(b)可以看出：真实启动压力梯度较大时，有效动用系数与油井井距的关系曲线比较陡峭，即有效动用系数对油井井距比较敏感，因而对于真实启动压力梯度比较大(渗透率相对较小)的储层而言，通过调整井距来提高有效动用系数较为容易；随着真实启动压力梯度的减小，有效动用系数对油井井距变化的敏感程度降低，因此，对于真实启动压力梯度较小(渗透率相对较大)的储层而言，通过调整井网井距的方式来提高有效动用系数，效果不会很明显。
综合上述分析得到：对于渗透率较大的储层，通过放大注采压力差的方式来改善开发效果较为容易；而对于渗透率较小的储层，通过调整井距来改善开发效果则更为有效。
3 实例应用
应用上述研究成果对江苏油田花17断块E1f31和E1f32 2个典型特低渗透储层的现有井网进行了评价，提出了井网调整方案并绘制了方便现场使用的有效动用系数理论图版。
江苏油田花17断块2006年投入开发，其主要的含油层系为阜宁组阜三段的E1f31和E1f32，两层系为典型的特低渗透储层：E1f31的有效渗透率为3.6×10-3 μm2，E1f32的有效渗透率为2.5×10-3 μm2，利用改进的特低渗透油藏物理模拟实验测试得到了二者的非线性渗流曲线并计算出了特征值。井网部署上，两层系均采用不规则三角形井网，共投产采油井17口，注水井6口，井排距250 m左右，从初期开发效果来看，E1f31层系较好。
按照本文方法对花17断块的井网进行了评价，评价结果如表1所示。从有效动用系数来看，E1f31层系比E1f32层系容易动用，这与油田的开发效果一致，建议参考表1的方案对E1f32层系的井网进行调整。
为了方便油田现场进行井网设计和调整，制作了有效动用系数理论图版，共计24幅，现举两幅予以说明：图7(a)所示为E1f31层系有效动用系数图版，图7(b) 所示为 E1f32层系有效动用系数图版，二者均是在注采压力差为7.8 MPa，BE/BC为0.5的情况下绘制的。利用这些图版可以对现有井网进行快速评价，进而判断是否需对井网实施调整以及如何调整，也可以用于指导新井网的设计和部署。例如：假设2个层系均要部署排距与井距比为0.8的等腰三角形井网，由图7可知：要达到理想的开发效果，对于E1f31层系而言，油井井距应小于275 m，而对于E1f32层系而言，油井井距应小于220 m。
表1 江苏油田花17断块井网评价与建议
Table 1 Well pattern evaluation & proposal for Hua17 Block in Jiangsu Oil Field
图7 有效动用系数图版举例
Fig.7 Plates of effective development coefficient for Hua 17 Block
4 结论
(1) 针对特低渗透断块油藏的井网形式，从非线性渗流基本公式出发，应用流管积分法推导了不规则三角形井网有效动用系数的计算公式，研究工作进一步完善了特低渗透油藏井网部署的油藏工程方法。
(2) 深入分析了注采压力差、井网几何形状以及非线性渗流曲线对有效动用系数的影响，分析结果表明：均质各向同性特低渗透断块油藏适合部署等腰或近等腰三角形井网；当井网形状偏离等腰三角形程度较高时，存在引起有效动用系数突变的注采压力差和油井井距；渗透率较大的储层，宜通过放大注采压力差来改善开发效果，而渗透率较小的储层，缩小井距则为更有效的手段。
(3) 应用本文方法对江苏油田花17断块现有井网进行了评价，评价结果与实际开发效果符合，并绘制了有效动用系数图版，以方便油田现场查看使用，应用结果表明，该方法可用于指导特低渗透断块油藏的井网设计、评价和调整。
参考文献：
[1] 冯文光. 非达西低速渗流的研究现状与展望[J]. 石油勘探与开发, 1986, 13(4): 76-80.
FENG Wen-guang. Progress of studies on the mechanism of non-Darcy low-velocity fluid flow[J]. Petroleum Exploration and Development, 1986, 13(4): 76-80.
[2] 黄延章. 低渗透油层渗流机理[M]. 北京: 石油工业出版社, 1998: 12.
HUANG Yan-zhang. Percolating flow mechanism of low permeability reservoir[M]. Beijing: Petroleum Industry Press, 1998: 12.
[3] 邓英尔, 刘慈群. 低渗透油藏非线性渗流规律数学模型及应用[J]. 石油学报, 2001, 22(4): 72-77.
DENG Ying-er, LIU Ci-qun. Mathematical model of nonlinear flow law in low permeability porous media and its application[J]. Acta Petrolei Sinica, 2001, 22(4): 72-77.
[4] 杨正明, 张英芝, 郝明强, 等. 低渗透油田储层综合评价方法[J]. 石油学报, 2006, 27(2): 64-67.
YANG Zheng-ming, ZHANG Ying-zhi, HAO Ming-qiang, et al. Comprehensive evaluation of reservoir in low-permeability oilfields[J]. Acta Petrolei Sinica, 2006, 27(2): 64-67.
[5] 许建红, 程林松, 周颖, 等. 一种求解低渗透油藏启动压力梯度的新方法[J]. 石油勘探与开发, 2007, 34(5): 594-597.
XU Jian-hong, CHENG Lin-song, ZHOU Ying, et al. A new method for calculating kickoff pressure gradient in low permeability reservoirs[J]. Petroleum Exploration and Development, 2007, 34(5): 594-597.
[6] 李松泉, 程林松, 李秀生, 等. 特低渗透油藏非线性渗流模型[J]. 石油勘探与开发, 2008, 35(5): 606-612.
LI Song-quan, CHENG Lin-song, LI Xiu-sheng, et al. Non-linear seepage flow models of ultra-low permeability reservoirs[J]. Petroleum Exploration and Development, 2008, 35(5): 606-612.
[7] 熊伟, 雷群, 刘先贵, 等. 低渗透油藏拟启动压力梯度[J]. 石油勘探与开发, 2009, 36(2): 232-236.
XIONG Wei, LEI Qun, LIU Xian-gui, et al. Pseudo threshold pressure gradient to flow for low permeability reservoirs[J]. Petroleum Exploration and Development, 2009, 36(2): 232-236.
[8] 时宇, 杨正明, 黄延章. 低渗透储层非线性渗流模型研究[J]. 石油学报, 2009, 30(5): 731-734.
SHI Yu, YANG Zheng-ming, HUANG Yan-zhang. Study on non-linear seepage flow model for low-permeability reservoir[J]. Acta Petrolei Sinica, 2009, 30(5): 731-734.
[9] 杨正明, 于荣泽, 苏致新, 等. 特低渗透油藏非线性渗流数值模拟[J]. 石油勘探与开发, 2010, 37(1): 94-98.
YANG Zheng-ming, YU Rong-ze, SU Zhi-xin, et al. Numerical simulation of the nonlinear flow in ultra-low permeability reservoirs[J]. Petroleum Exploration and Development, 2010, 37(1): 94-98.
[10] 计秉玉, 李莉, 王春艳. 低渗透油藏非达西渗流面积井网产油量计算方法[J]. 石油学报, 2008, 29(2): 256-261.
JI Bing-yu, LI Li, WANG Chun-yan. Oil production calculation for areal well pattern of low-permeability reservoir with non-Darcy seepage flow[J]. Acta Petrolei Sinica, 2008, 29(2): 256-261.
[11] 计秉玉, 王春艳, 李莉, 等. 低渗透储层井网与压裂整体设计中的产量计算[J]. 石油学报, 2009, 30(4): 578-582.
JI Bing-yu, WANG Chun-yan, LI Li, et al. Calculation method for production rate of rectangular well pattern and fracturing integration production mode in low-permeability reservoir[J]. Acta Petrolei Sinica, 2009, 30(4): 578-582.
[12] 何英. 低渗透油藏井网部署的油藏工程方法研究[D]. 廊坊: 中科院渗流流体力学研究所, 2009: 67-95.
HE Ying. Study on well pattern arrangement of low permeability reservoir by reservoir engineering methods[D]. Langfang: CAS. Institute of Porous Flow and Fluid Mechanics, 2009: 67-95.
[13] 刘德华, 喻高明, 欧阳传湘, 等. 小断块油藏井网密度研究[J]. 江汉石油学院学报, 2001, 23(1): 43-45.
LIU De-hua, YU Gao-ming, OUYANG Chuan-xiang, et al. Well pattern arrangement in small fault block oil reservoir[J]. Journal of Jianghan Petroleum Institute, 2001, 23(1): 43-45.
[14] 杨清立, 杨正明, 王一飞, 等. 特低渗透油藏渗流理论研究[J]. 钻采工艺, 2007, 30(6): 52-54.
YANG Qing-li, YANG Zheng-ming, WANG Yi-fei, et al. Study on flow theory in ultra-low permeability oil reservoir[J]. Drilling & Production Technology, 2007, 30(6): 52-54.
(编辑 陈爱华)
收稿日期：2011-05-12；修回日期：2011-07-26
基金项目：国家自然科学基金资助项目(10672187)；国家科技重大专项项目(2008ZX05000-013-02)
通信作者：齐亚东(1984-)，男，河北丰润人，博士研究生，从事特低渗透油藏开发理论研究；电话：010-69213294；E-mail: qiyadong007@163.com
