J. Cent. South Univ. (2013) 20: 563–571
DOI: 10.1007/s11771-013-1519-6

Signal timing optimization model based on dual-ring phase scheme for roundabout
MA Wan-jing(马万经), XIE Han-zhou(谢涵洲), BAI Yu(白玉), ZHAO Jing(赵靖), YANG Xiao-guang(杨晓光)
Key Laboratory of Road and Traffic Engineering of Ministry of Education (Tongji University),Shanghai 201804, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2013
Central South University Press and Springer-Verlag Berlin Heidelberg 2013
Abstract: A signal optimization model for roundabout was proposed based on dual-ring scheme and two stop lines for left turns control concept were used to eliminate the conflict points and weaving sections at a roundabout. A cycle length minimization problem was considered to generate optimal signal timings for roundabout, and a set of constraints to ensure feasibility and safety of the resulting optimal signal settings were proposed. Extensive experimental analyses in comparison with signalized intersection reveal that the proposed model is quite promising for application in design of roundabout signals, and the minimum cycle length can decrease from 186 s to 79 s while the capacity increases from 8 682 pcu/h to 9 011 pcu/h under high demand scenario. Sensitivity analysis with respect to the system performance show that the lane assignment plan, number of circulatory lanes and left turn ratio are three critical factors which have dominate impacts on performance of signalized roundabout
Key words: signalized roundabout; dual-ring phase; single timing optimization; left-turn movement
1 Introduction
Roundabout is a type of priority controlled intersections [1]. The modern roundabout was developed in the UK in the 1 960 s and modern roundabouts provide substantially better operational and safety characteristics than older traffic circles and rotaries [2]. Therefore, many countries have adopted them as common intersection form. It is estimated that until April 2 010, over 2 000 roundabouts have been built in the United States [3] and more of those exist in Chinese cities. Roundabouts without traffic signal control have been intensively studied and widely used [4–7].
The bottlenecks of an unsignalized roundabout with two or more circulatory lanes are weaving sections, where the vehicles enter or leave the roundabout [8]. Then, the typical disadvantage of roundabout, especially for multi-lane roundabout, is that it cannot handle high traffic demands due to particular characteristics of weaving areas [9]. In order to solve this problem, traffic signals are used and installed on the approaches of a roundabout in the limited literatures [10]. As one of the efforts to address the above critical operational issues, YANG et al [11] proposed a new method of traffic-signal control, two-stop line-for-left-turn (TSLT), for modern roundabouts to eliminate the conflict points and weaving sections at a roundabout using traffic signals installed both on entry approaches and on the circulatory carriageway. It was shown that by installing traffic signals both on entry approaches and on the circulatory carriageway, substantial improvement in the roundabout performance can be achieved. However, the relationship of signal timings between all approaches, either for left-turning and straight-ahead movements, has not been analyzed systematically. Moreover, most of the models proposed in literatures focused on delay minimization problem. It is very difficult to correctly calculate vehicle delay because part of vehicles has to stop again at carriageway after passing stop line at entry approach, and the problem of minimizing delay involves a non-linear objective function not easy to solve.
In response to the aforementioned concerns, this work presents an optimization model based on well-designed dual-ring phase scheme. Attention is given to cycle length minimization problem in this work. Minimum feasible cycle length can lead to satisfactory delay and operating condition, and capacity of intersection can increase by increasing cycle length under a given traffic flows and geometric configuration.
2 Basic control concept
2.1 Two-stop-line-for-left-turn control (TSLT)
Figure 1(a) shows a typical signalized four-leg roundabout layout. There are two stop lines for each left
turn movements on approach and circulatory roadway. Taking direction 1–3(i=1–3, as shown in Fig. 1) as an example, the basic idea of TSLT is:
1) Through traffic and left turn traffic use different lanes, controlled by different signals respectively;
2) Between two stop lines for every left turn movement, one is located at entering approach, and the other is located on opposite circulatory lanes. Taking left turn movement on approach i=1 as an example, the first stop line is P-P′ line and the second stop line is N-N′ line;
3) The left turn movement before first stop line (e.g.it is line P-P′ for approach 1) gets green signal while through traffic keeps moving, and queues before the second stop lines (for approach 1, it is line N-N′) on the circulatory roadway(Fig. 1(b));
4) Both through movement and left turn movement before first stop lines get red signal while left turn traffic queuing before the second stop lines gets green time (Fig. 1(c));
5) The signal for second stop lines of directions 2–4 turn to red and the through movement of directions 2–4 get green signals and entering the roundabout (Fig. 1(d)).
Note that, signals at second stop lines for left turn movements from approach 1 and approach 3 show green both in Fig. 1(c) and Fig. 1(d) while the function of green time is different. Green time in Fig. 1(c) is used to clear all the left turn vehicles from approaches 1 and 3 which have entered into the roundabout, while green time in Fig. 1(d) is used to make circulatory carriageway available for through and left movement of approaches 2 and 4. Only the first part of green time (green time in Fig. 1(c)) is included in the optimization process of green time of phase for left turn before second stop line in this work.
2.2 Design of phase scheme
Figure 2 shows the phase combinations for a four- arm signalized roundabout based on dual-ring concept. A phase combination consists of a series of concurrent phases, and all relevant movements, including through movements, left turns before first stop lines, and left turns before second stop lines are considered. The left turn phases for left movements before first stop lines are combined with through phases at the same approach because they have no conflicts with opposite through movements under TSLT control. The left turn phases for left turn movements before second stop lines represent the original left turn phase position in the dual-ring scheme. Ten variables, xj (j= 1, 2, ···, 10), are defined to represent the relationship of all phase time based on the dual-ring structure, as shown in Fig. 2.
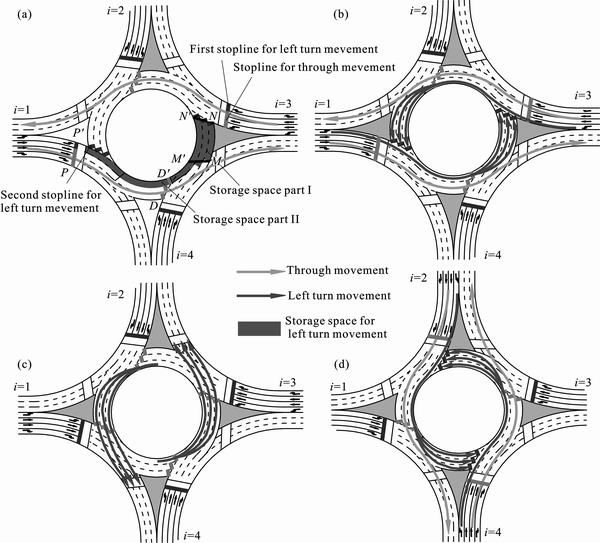
Fig. 1 Two-stop line-for-left-turn control concept

Fig. 2 Design of phase scheme
As stated above, the phases indicated by x3, x4, x5, x6, in Fig. 2 are virtual phases, and they represent the green time for releasing the queue of the left turn vehicles which have entered into the roundabout during previous phase, as shown in Fig. 1(c). However, the traffic lights on these second stop lines should still be green after dispersing those queuing left turn movements in order to release through movements of next phase, as shown in Fig. 1(d).
3 constraints
3.1 Storage space for left turn movement before second stop line
Left turn movements passing first stop line may have to wait at the second stop line on circulatory carriageway for green time, so that the queuing area on circulatory carriageways should be large enough to accommodate them. The storage space is composed by two parts, as shown in Fig 1(a): Storage space part I, queuing area composed by all circulatory lanes (decided by Aci and Nc); and Storage space part II, queuing area composed by parts of circulatory lanes (decided by ALi and 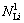 ).
).
As shown in Fig. 1(a), in storage space part 1, Ai is the area of storage space for left turn movement of approach i before second stop line (pcu); Aci is average length of one circulatory lane in the storage space that only part of circulatory lanes can be used for queuing of left turn movement of approach i, (pcu) 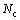 is the number of circulatory carriageway,
is the number of circulatory carriageway, 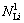 and
and  are the numbers of lanes for left turn movements before first stopline and second stop of approach i, respectively; and
are the numbers of lanes for left turn movements before first stopline and second stop of approach i, respectively; and  is average length of one circulatory lane in the storage space that only part of circulatory lanes can be used for queuing of left turn movement of approach i, (pcu). Taking left turn movement of approach 1 as an example, the
is average length of one circulatory lane in the storage space that only part of circulatory lanes can be used for queuing of left turn movement of approach i, (pcu). Taking left turn movement of approach 1 as an example, the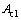 is the length of one circulatory carriageway from line M–M′ to N–N′ which decided by the radius of the roundabout. In storage space part I, the
is the length of one circulatory carriageway from line M–M′ to N–N′ which decided by the radius of the roundabout. In storage space part I, the 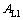 is the length of one lane from line P-P′ to line M–M′. Then, the total area of queue storage space for left turn movement before second stop lane can be expressed as
is the length of one lane from line P-P′ to line M–M′. Then, the total area of queue storage space for left turn movement before second stop lane can be expressed as
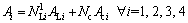 (1)
(1)
The number of left-turn vehicles which have passed first stop line should be less than the total area of queue storage space before these vehicles get green time at second stop line.
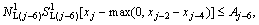
 (2)
(2)
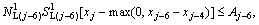
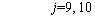 (3)
(3)
In Eq.(2), (xj–max(0, xj–2–xj–4)) and (xj–max(0, xj–6–xj–4)) mean the length of time between starting time of green at first stop line and starting time of green at second stop line of left movements 1, 2 and 3, 4, respectively. Waiting area should be large enough to accommodate all left turn vehicles passing first stop line during this time span.
3.2 Maximum acceptable degree of saturation
Let aiT and aiL be the maximum acceptable degrees of saturation of through movement and left turn movement before first stop line on approach i, respectively; 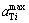 and
and 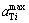 are the maximum acceptable degrees of saturation of through movement and left turn movement on approach i, respectively; C is cycle length (s),
are the maximum acceptable degrees of saturation of through movement and left turn movement on approach i, respectively; C is cycle length (s),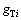 ,
,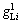 and
and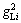 are green time for through movement, left movement before first stopline and left movement before second stopline of approach i (s), respectively;
are green time for through movement, left movement before first stopline and left movement before second stopline of approach i (s), respectively;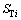 ,
,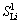 and
and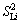 are saturation flow of one through lane, one left lane before first stopline and one left turn lane before second stopline of approach i (pph), respectively; Therefore, the degree of saturation of each movement can be expressed as
are saturation flow of one through lane, one left lane before first stopline and one left turn lane before second stopline of approach i (pph), respectively; Therefore, the degree of saturation of each movement can be expressed as
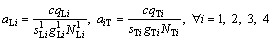 (4)
(4)
Then, the following constraints can be set to ensure that the degree of saturation is below the maximum acceptable limit:
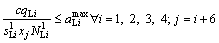 (5)
(5)
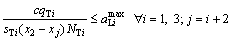 (6)
(6)
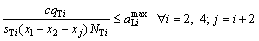 (7)
(7)
3.3 Capacity of left turns at second stop lines
The queuing area before the second stop line can be taken as an approach with short lanes. Let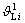 and
and represent capacities of left turn movement at first stopline and second stopline at approach i, respectively. Then, the capacity of left-turn vehicles on the circulatory roadway is related with the length of short lane area, and it can be expressed as
represent capacities of left turn movement at first stopline and second stopline at approach i, respectively. Then, the capacity of left-turn vehicles on the circulatory roadway is related with the length of short lane area, and it can be expressed as
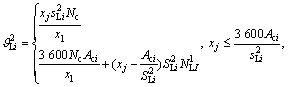
 (8)
(8)
In Eq. (8), 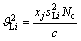 means that the all lanes
means that the all lanes
before the second stop line have been used fully during total green time if green time for left movement at second stop line is not larger than the minimum green time to clear all queues between lines N–N′ and M–M′.
Otherwise, only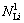 lanes can be used at rest of the left turn green time.
lanes can be used at rest of the left turn green time.
The capacity of the first stop line is decided by number of lanes and green split, and it can be expressed as
 (9)
(9)
In order to prevent gridlock of roundabout, the capacity of second stop line should be no less than that of the first stop line, and it can be expressed as
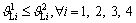 (10)
(10)
3.4 Clearance time
Two types of clearance time are included in the designed phase scheme for signalized roundabout, as shown in Fig. 2.
1) Clearance time type I: Normal clearance time for any pair of leaving movements (leaving from stop line on circulatory carriageways) and entering movements (entering from stop line on approach), the clearance time constraints are needed only when both movements are permitted altogether.
2) Clearance time type II: Clearance time between second stop line and nearest upstream first stop line. The clearance time is used to make sure that all vehicles passing nearest upstream first stop line on approach pass second stop line on circulatory carriageways.
3.4.1 Model for clearance time type I
The clearance time type I is related to several factors: vehicle speed, acceleration and deceleration, width of intersection and length of vehicle.
 (11)
(11)
where 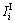 is clearance time of movements from approach i (s);
is clearance time of movements from approach i (s); 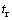 is driver’s perception-reaction time to traffic light indications (s); vv is the vehicle speed, (m/s); a is deceleration rate (m/
is driver’s perception-reaction time to traffic light indications (s); vv is the vehicle speed, (m/s); a is deceleration rate (m/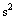 ); w is intersection width (m); and L is length of vehicle (m).
); w is intersection width (m); and L is length of vehicle (m).
3.4.2 Model for clearance time type II
The clearance time type II should ensure that the last vehicle passing first stop line on approach at the last second of green time should cross next nearest stop line on circulatory carriageway before the relevant signals changing from green to red. Taking approach 1 as an example, the next nearest stop line on circulatory carriageways is line D–D′. In order to clear circulatory carriageways, vehicles coming from line P–P′ should passing line D–D′ before the signals on D–D′ changing from green to red and signals on approach 4 changing from red to green. Then, the clearance time type II can be expressed as
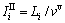 (12)
(12)
where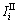 is length of clearance time type II of movement for approach i (s).
is length of clearance time type II of movement for approach i (s).
3.5 Duration of green time
The duration of green time for each vehicle phase should follow the constraints of minimum green time and maximum green time, which can be specified as
 (13)
(13)
 (14)
(14)
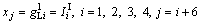 (15)
(15)
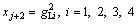 (16)
(16)
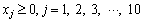 (17)
(17)
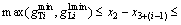
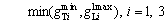 (18)
(18)

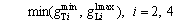 (19)
(19)
 (20)
(20)
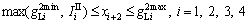 (21)
(21)
where, 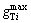 and
and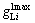 are maximum green time for through movement and left turn movement of approach i (s);
are maximum green time for through movement and left turn movement of approach i (s); and
and 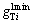 are minimum green time for through and left turn movement of approach i(s), respectively. Equations (13)–(16) represent the relationship between green time of each phase and the ten variables defined in the dual ring phase scheme, and Eqs. (16)–(20) represent the constraints of minimum and maximum green time constraints. Equation (21) represents that the minimum green time of phases 3, 4, 5, and 6 as shown in Fig. 2(b) should be larger than the clearance time Type II, respectively.
are minimum green time for through and left turn movement of approach i(s), respectively. Equations (13)–(16) represent the relationship between green time of each phase and the ten variables defined in the dual ring phase scheme, and Eqs. (16)–(20) represent the constraints of minimum and maximum green time constraints. Equation (21) represents that the minimum green time of phases 3, 4, 5, and 6 as shown in Fig. 2(b) should be larger than the clearance time Type II, respectively.
3.6 Cycle Length
The duration of cycle length should follow the constraints of minimum and maximum values, Cmin and Cmax, and the sum of total green time and clearance time should be equal with cycle length, which can be specified as
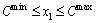 (22)
(22)
4 Optimization of signal settings
To summarize Sections 2 and 3, the control variables can now be specified as green time of each vehicular movement, i.e. x, i=1, 2, ···, 10.
The cycle length minimization is selected as the objective function. Compared delay minimization and other criteria which involves a non-linear objective function, the cycle length minimization problem can be effectively formulated as MILP problems and solved by standard branch-and-bound routines, and experience shows that for specified cycle length problems, the cycle length minimization design would normally perform satisfactorily, even if the delay incurred by users is concerned. The cycle length minimization problem can therefore be formulated as the following MILP:
Minimize: x1
The set of constraints variables is given in Eqs. (2)– (3) and (5)–(22).
5 Model evaluation and analyses
5.1 Experiment at design
To illustrate the applicability of the proposed model, we employ a roundabout in Xiamen, China, for numerical tests. The diameter of central island is 70 m, and basic layouts of the arterial and phase configurations are given in Fig. 3. All pedestrians and bicycles crossing streets by an elevated pedestrian bridge and do not present at surface of intersection.
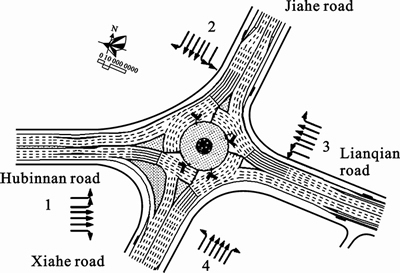
Fig. 3 Experimental roundabout layout and lane markings
The saturation flows for straight-ahead movements and left turn movements are taken as 1 800 and 1 700 pcu/(h×lane), respectively. It is assumed that all turning radii are 12 m for all cases of studies. The maximum and minimum cycle length is set to be 200 s and 30 s, respectively, and the maximum acceptable degrees of saturation are 1 on all lane groups. The minimum and maximum green durations are 5 s and 40 s for all traffic movements. The effective green is always equal to the actual green in the calculation.
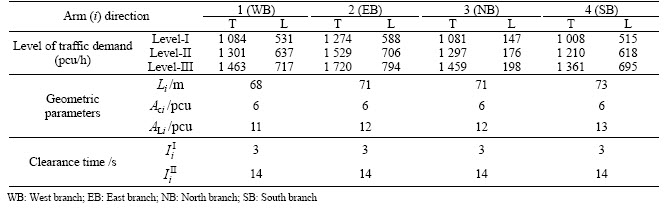
The traffic demands, geometric parameters, and clearance time are given in Table 1. This numerical test includes three volume levels: low (basic level I), medium (1.2 times of basic level II), and high (1.35 times of basic level III) designed to test the performance of proposed control model.
Table 1 Parameters used in numerical test
5.2 Experimental results and analysis
In this section, the performance of signalized roundabout will be compared with normal signalized intersection. To ensure a fair comparison, the signalized intersection has the same geometry configurations, e.g., same number of approaches, same number of lanes for every movement and so on, and signal timing plans was generated using the same optimization scheme based on dual-ring phase structure.
1) Signalized roundabout: implement signal control with the signal settings generated by the proposed model;
2) Signalized intersection: the central island is removed and the roundabout is changed to a normal four arms intersection controlled with the normal dual ring phase scheme.
Step 1: Comparison based on field data
The optimal signal plans for all levels of traffic demand are shown in Fig. 4. It can be seen that the complicated cycle structure is formed automatically during optimization, and signal timings for both first stop line and second stop line can be generated by the proposed model. Figure 5 shows the capacity comparison results from the proposed model under different demand levels defined in Table 2.
The minimum cycle length of both signalized roundabout and intersection increases with the increase of traffic demand as shown in Fig. 4. For the demand level-II and demand level-III scenarios, a shorter cycle length was obtained from the proposed model for signalized roundabout compared with normal intersection. Moreover, the signalized roundabout outperforms intersection in terms of total capacity at all scenarios, as shown in Fig. 5. The reason is that the green time needed for left turn movement on second stop line (which is one of critical parts of a cycle as shown in Fig. 2(b)) is decided by clearance time (14 s as given in Table 2) rather than saturation of degree of left turn movement under the situation of low traffic volume, and it is higher than minimum green time needed for a left turn movement if left turn volume is not large enough. Moreover, the left turn movements and through movements can get the same green time at same time as long as the storage space on circulatory lanes before second stop line is large enough for queuing.

Fig. 4 Optimal signal settings for examples(Unit: s):
Table 2 Composition of cycle length

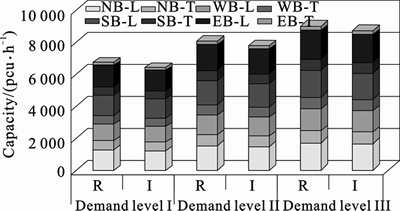
Fig. 5 Capacity under different control scenarios
Step 2: Sensitivity analysis of critical parameters
1) Impacts of left turn ratio
Based on the above analysis, left turn movements have very important impacts on total performance of a signalized roundabout. Then, the impacts of ratio of left turn movements were investigated. It was assumed that there are 5 lanes on each approach and 2 for left turn and 3 for through movement, and the traffic demand of every approach is the same and it ranges from 1 500 pcu/h to 2 100 pcu/h. The minimum cycle lengths at all levels of traffic demand and left turn ratio are shown in Fig. 6. From Fig. 6, it can be seen that the performance of signalized roundabout is closely related with left turn ratio, and so does normal intersection. The minimum cycle length for signalized roundabout is higher than that for intersection under low traffic volume. The advantages of signalized roundabout become more apparent with the increase of total traffic volume. The minimum cycle length for signalized roundabout is much lower than that for intersection almost at all left turn ratio situations under heavy traffic demand scenario. Compared with normal intersection, the trend of change of minimum cycle length with the increase of left turn ratio is not the same. The minimum cycle length of normal intersection increases with the increase of left turn ratio, while the minimum cycle length for signalized roundabout goes down to a lowest point and then goes up.

Fig. 6 Impact of left turn ratio:
The composition of cycle length is further analyzed in Table 2. Because the signal timings of all approaches are same, only related signal timings of one approach are shown, including green time of through movements, left movements at first stop line, and left movements at second stop line. In Table 2, T-green means green time of through movement (gT), L-green means green time of left movement at first stopline (gL), C-time means clearance time of left movement at second stopline (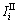 ), R-time means minimum green time needed to release left turn vehicles to pass first stopline.
), R-time means minimum green time needed to release left turn vehicles to pass first stopline.
For normal intersection, both the through green time and left turn green time as given in Table 2 are two components of a cycle. However, for signalized roundabout, the maximum green time for through movement and left movement and the maximum time of clearance time and minimum release time (light-gray numbers) are the two kinds of components of a cycle. For signalized roundabout, with fixed total demand, the green time for left movements will increase with the increase of left turn ratio and become the decision part compared with green time for through movement. In the same way, the minimum release time will become the decision part if left turn ratio is large enough, as shown in Table 2.
2) Impacts of lane assignment
Three scenarios, total demand 1 500 puc/h, left turn ratio 0.74 (s1), total demand 1 800 puc/h, left turn ratio 0.62 (s2) and total demand 2 100 pcu/h, left turn ratio 0.53 (s3) in Table 2 were selected to evaluate the impacts of lane assignment plan on performance of roundabout because the minimum cycle lengths for roundabout are extremely high under those situations.
As shown in Fig. 7, the minimum cycle length is closely related with lane assignment plans. With optimal lane assignment plan, the minimum cycle length can decrease dramatically (minimum cycle lengths decrease by 79.6%, 84.8% and 75% for s1, s2, and s3, respectively). Based on the above analysis results, it is highly recommended that lane assignment plans should be evaluated along with the optimization of signal timings for a roundabout.
3) Impacts of number of circulatory lanes
As indicated in Fig. 8 (D in the legend means traffic demand and CL means number of circulatory lanes.), in all demand levels, for the low left turn ratio scenarios, a same cycle length was obtained from the proposed model with the objective of minimizing the cycle length under different circulatory lanes situations. However, for high left turn ratio scenarios, a much shorter cycle length was obtained under 5 circulatory lanes compared with that under 4 circulatory lanes. Therefore, the number of circulatory lane have dramatic impacts on performance of a signalized roundabout under higher left turn demand while have no impacts under low left turn demand situations due to the release time on second stop line, which is directly decided by number of circulatory lanes and will play an critical role only under higher left turn demand situations.
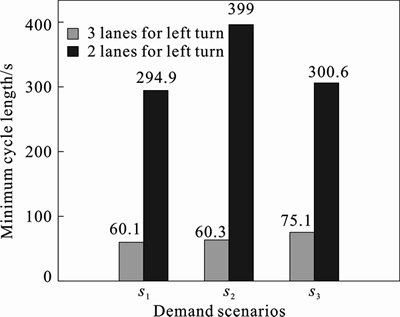
Fig. 7 Impacts of lane assignment on cycle length
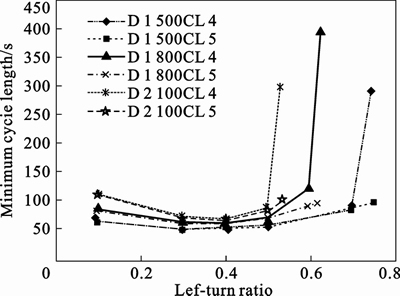
Fig. 8 Impacts of number of circulatory lanes
5 Conclusions
1) An optimization model for design of roundabout signal timings is developed, and a set of constraints to ensure feasibility and safety of the resulting optimal signal settings are proposed.
2) The numerical results have confirmed that the roundabout controlled by proposed method can outperform normal signalized intersection, especially under high demand situation.
3) Results of sensitivity analyses show that factors including left turn ratio, traffic demand, and the number of circulatory lanes have dominate impacts on the performance of signalized roundabout.
4) Note that this work has presented preliminary evaluation results for the proposed model. More extensive numerical experiments or field tests will be conducted to assess the effectiveness of the proposed model.
References
[1] Transportation Research Board of the National Academies. Delivery draft chapter 21: Roundabouts. Highway Capacity Manual [M]. Washington D. C.: Transportation Research Board Press, 2010.
[2] HALLWORTH M S. Signaling roundabouts [J]. Traffic Engineering and Control, 1992, 33(6): 46–51.
[3] INSURANCE INSTITUTE FOR HIGHWAY SAFETY. Q&As: Roundabouts. Insurance Institute 40 for Highway Safety, Highway Loss Data Institute [EB/OL]. [2010–4–30]. http://www.iihs. org/research/qanda/roundabouts.html.
[4] RODEGERDTS L, BLOGG M, WEMPIE E, et al. Roundabouts in the United States [R]. Washington D. C: NCHRP Report 572,Transportation Research Board of the National Academies, 2007.
[5] AL-OMARI B H, AL-MASAEID H R , AL-SHAWABKAH Y S. Development of a delay model for roundabouts in Jordan [J]. Transport Eng, 2004, 130(1): 76–82.
[6] AL-MADANI H M N. Dynamic vehicular delay comparison between a police-controlled roundabout and a traffic signal [J]. Transportation Research A, 2003, 37(8): 681–688.
[7] SACCOMANNO S F, CUNTO F, GUISEPPE G, VITALE A. comparing safety at signalized intersections and roundabouts using simulated rear end conflicts[C]// Transportation Research Board Annual Meeting. Washington D. C 2008: 90–95
[8] MARILYN V, RUEY L C, CARLOS D. Operations of a modern roundabout with unbalanced approach volume[C]// Transportation Research Board Annual Meeting Washington D C, 2011: 234–243
[9] AKCELIK R. A roundabout case study comparing capacity estimates from alternative analytical models[C]// Urban Street Symposium, Anaheim, California, USA, 2003: 1–20.
[10] DIXIT, V V, RADWAN E. Roundabout capacity: A New Perspective[C]// Transportation Research Board Annual Meeting. Washington D C, 2008: 08-1399.
[11] YANG X, LI X, XUE K. A new traffic-signal control for modern roundabouts: method and application [J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 282–287
(Edited by HE Yun-bin)
Foundation item: Project(51178345) supported by the National Natural Science Foundation of China; Project(2011AA110305) supported by the National High Technology Research and Development Program of China; project supported by the Program for Young Excellent Talents in Tongji University, China
Received date: 2011–12–08; Accepted date: 2012–04–10
Corresponding author: BAI Yu, PhD, Associate Professor; Tel: +86–21–69584674; E-mail: baiyu@tongji.edu.cn